高阶非线性系统自适应模糊有限时间状态约束控制
范彦丽 李永明 佟绍成
0 引言
在过去十几年中,学者们对高阶非线性系统控制问题的关注度逐年提高,并取得了一些有价值的理论成果[1-4].相对于文献[5-6] 中严格反馈非线性系统,高阶非线性系统在线性化过程中存在不可控情况,同时虚拟和实际控制输入中存在指数幂次pi,这增加了控制器的设计难度,因此传统的反步递推方法不再适用.为了解决高阶非线性系统的控制问题,Lin等[1]在反步递推方法的基础上首次提出了加幂积分控制技术.随后,许多学者利用加幂积分方法对高阶非线性系统进行了广泛研究.文献[2-3]针对单输入单输出高阶非线性系统,研究了状态反馈和输出反馈控制设计问题,在Lyapunov稳定意义下,保证了被控系统渐近稳定.
值得注意的是,渐近稳定不能给被控系统提供更高精度的控制方案.在飞行器姿态、感应电机等实际控制中,一般希望控制系统能在有限时间内满足期望的控制性能.此外,有限时间控制具有许多潜在的好处,如较强的收敛速度和较强的鲁棒性等.因此,近几年有限时间控制问题的研究取得了很大的进展.文献[7-8]通过加幂积分技术和齐次占优技术,研究了高阶非线性系统的全局有限时间控制问题;文献[9]针对一类具有参数不确定性的非线性系统在给定的瞬态指标基础上,提出了一种自适应有限时间控制方法;文献[10]基于扰动观测器讨论了一类不确定非线性系统的终端滑模控制;文献[11-12]分别针对严格反馈和非严格反馈非线性系统,基于自适应模糊和神经网络控制方法,在有限时间Lyapunov稳定理论的框架下,保证了被控系统实际有限时间稳定.虽然上述工作[7-12]对非线性系统的有限时间控制设计问题进行了相应的研究,但仍存在一些问题值得进一步研究.
除了稳定性问题,当考虑到性能规格以及安全等因素,非线性系统会受到状态或输出的约束,在系统运行期间,如果状态或输出违反约束条件,可能会使系统性能下降或损坏.文献[13]结合时变非对称障碍Lyapunov函数,对一类具有全状态约束的严格反馈非线性系统,提出了一种自适应跟踪控制方案;文献[14]对一类非三角结构系统,在考虑执行器故障和误差约束的条件下,提出了一种自适应模糊控制方案.通过结合tan型障碍Lyapunov函数,文献[15-16]针对具有部分状态约束和全状态约束的高阶非线性系统,分别构造了两种不同的控制器.但是上述工作[13-16]均未考虑有限时间控制.在实际工程中,如机器人机械手、电机系统等,不仅存在状态约束现象,而且需要考虑系统的收敛时间问题.近些年来,许多学者致力于非线性系统的状态约束和有限时间控制问题的研究,并取得了许多具有标志性的成果[17-20].文献[17-18]分别针对具有死区非线性和切换行为的非线性系统,研究了有限时间全状态约束控制设计问题;文献[20]将文献[17-18]所提出的控制设计算法应用到了实际直流电机系统.在文献[17-20]所考虑的非线性系统中,虚拟控制和实际控制的幂次均为1.
受到以上研究成果的启发,本文针对一类非严格反馈高阶非线性系统,提出一种自适应模糊有限时间跟踪控制方法.结合反步递推法、加幂积分技术和障碍Lyapunov函数,设计了一种自适应有限时间控制器.所设计的控制器能够同时确保输出有限时间内跟踪给定的参考信号,且闭环系统的状态不超出给定的约束边界.与现有的文献相比,本文的贡献概括为以下三方面:
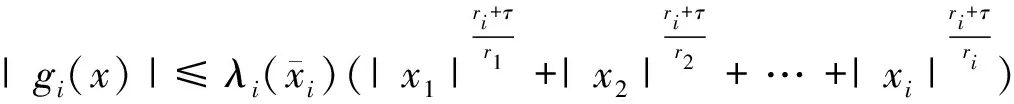
2) 相较于文献[17-20]系统幂次为1的约束问题,本文解决了控制输入幂次是正奇数比的非线性系统的状态约束控制问题.
3) 本文所设计的有限时间控制器不仅可以保证系统状态不超出给定约束边界,而且能确保闭环系统的所有信号在有限时间内收敛到包含原点的一个小邻域内.而文献[15-16]在系统满足状态约束条件下,没有考虑闭环系统收敛时间.
1 模型描述和预备知识
1.1 模型描述
考虑如下一类非线性系统:

(1)
其中:x=[x1,x2,…,xn]Τ∈Rn是系统的状态向量;u∈R和y∈R分别是系统的控制输入和输出;hi(x)和gi(x)是光滑未知非线性函数;指数pi(i=1,2,…,n)是两个正奇数的比值.x(0)=[0,…,0]Τ是系统的平衡点.对于任意给定的正常数kci,系统所有的状态收敛到给定的紧集内,即Ωxi={xi∈R||xi| (2) 引理1[6,14]在紧集Ω上定义连续函数h(x),对于任意给定正常数η>0,存在模糊逻辑系统Θ*Τφ(x),满足: (3) 引理2[17-19]考虑如下非线性系统: (4) 控制目标:对于系统(1),设计有限时间自适应模糊控制器,使得: 1)闭环系统的所有信号在有限时间内收敛到包含原点的一个小邻域内; 2)系统输出在有限时间内跟踪给定信号yr(|yr|≤y0,y0是已知正常数); 3)系统所有状态收敛到一个给定的约束边界内. 在本节中,基于自适应反步递推方法和加幂积分技术,设计模糊自适应有限时间控制器,同时依据引理2,结合所设计的控制器证明系统(1)是半全局实际有限时间稳定的. 定义坐标转换: (5) 步骤1.根据式(1)和(5),β1的导数为 (6) 定义如下障碍Lyapunov函数: 对治疗后患者的症状进行评估,显效为再无心肌梗死症状,有效为心肌梗死的心绞痛程度有所改善,无效为症状无变化甚至出现加重现象,显效率与有效率之和为治疗的总有效率。 (7) (8) (9) (10) 根据Young不等式[14]: (11) (12) 其中,υ1>0,σ1>0是设计参数.将式(12)代入式(10),可得: (13) (14) (15) (16) (17) 其中,e2>0是一个设计参数. 根据式(17),式(16)可重写为 (18) 步骤i(2≤i≤n-1).在这一步中,引入障碍加幂积分技术.定义如下标量函数 (19) 选取如下Lyapunov函数: (20) (21) 根据式(19),可得: (22) (23) 根据式(23)和不等式|aη-bη|≤21-η|a-b|η[18](a,b∈R且0<η<1),可得: (24) 其中,bi≥(1/ri)×21-1/ri. 同理可得: (25) 将式(22)—(25)代入式(21),可得: (26) 令 (27) (28) (29) 根据Young不等式,可得: (30) 其中,υi>0,σi>0是设计参数. 将式(30)代入式(29),可得: (31) (32) (33) (34) 步骤n.选取如下Lyapunov函数: (35) (36) (37) (38) 根据式(31),(32)和(33),可得Vn的导数为 (39) (40) (41) 下面的定理给出了所设计的有限时间控制器所具有的性质. 定理1针对非线性系统(1),在假设1的条件下,控制器(37),虚拟控制函数(14)、(32)和参数自适应律(15)、(33)和(38),能保证: 1)闭环系统的所有信号半全局实际有限时间稳定,且输出信号y在有限时间内跟踪给定信号yr; 2)系统状态xi(t)不超出给定的约束边界kci. 证明选取如下Lyapunov函数: (42) 注意到,对于任意给定正常数kb1,β1满足|β1| (43) 根据式(42)和式(43),可得: (44) 对于τ∈(0,1)一定存在一个常数=(1+τ)/2,使得∈(0,1).结合式(44),进一步可得到: (45) 根据式(41)和(45),可得: (46) 类似于式(40),以下不等式成立: (47) (48) (49) 根据以上分析以及式(15),(33)和(38),得到: (50) 定理1证明完毕. 考虑如下非线性系统: (51) 选择隶属函数为 仿真结果如图1—6所示. 图1 状态x1与跟踪信号yr的轨迹Fig.1 Trajectories of state x1 and tracking signal yr 图2 状态x2的轨迹Fig.2 Trajectory of state x2 图3 控制器u的轨迹Fig.3 Trajectory of controller u 图4 跟踪误差β1和β2的轨迹Fig.4 Trajectories of tracking errors β1 and β2 图5 自适应参数的轨迹Fig.5 Trajectory of adaptive parameter 图6 自适应参数的轨迹Fig.6 Trajectory of adaptive parameter 根据仿真结果图1—6可知,系统的状态没有超出给定的约束边界,系统输出在有限时间内很好地跟踪给定的参考信号,同时闭环系统的所有信号在有限时间收敛到包含原点的一个小邻域内. 本文针对一类具有全状态约束的非严格反馈高阶非线性系统,在自适应模糊理论框架下,研究了一种有限时间自适应控制设计问题.首先,利用模糊逻辑系统对未知非线性函数进行辨识;其次,采用加幂积分技术,构造了一种新的障碍Lyapunov 函数,结合反步递推技术,解决了高阶非线性系统的有限时间状态约束问题;最后,通过有限时间Lyapunov稳定性理论,严格证明了跟踪误差的有限时间收敛性和闭环系统的半全局实际有限时间稳定性.

1.2 预备知识



2 模糊有限时间控制器设计和稳定性分析
2.1 模糊有限时间控制器设计







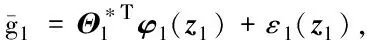







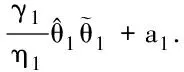
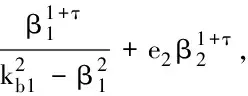




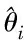


























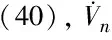

2.2 稳定性分析













3 仿真实例







4 结论

