基于事件触发机制的一类非严格反馈非线性系统的自适应神经网络追踪控制
廉玉晓 杨文静 王琳淇 王学良 夏建伟
0 引言
近年来,由于非线性系统被广泛地应用在实际生活中,因此相关的控制问题受到广泛的关注.在对非线性系统的研究中,反步技术成为处理非线性系统相关问题的有力工具之一[1-2].基于反步技术,文献[3]研究了一类带有全状态约束的随机非线性系统的自适应追踪控制问题.然而,当非线性系统中的非线性函数不再是完全已知或者具有未知参数的线性形式时,仍然使用传统的反步控制技术研究此类系统会有一定的困难.因此,基于上述分析,大量的有关模糊逼近和神经网络的控制策略[4-9]被提出.例如,文献[7]结合反步技术和模糊逻辑系统针对一类带有时滞的随机非线性系统设计了一种自适应追踪控制方案.
值得注意的是,上述所提到的文献[7]研究的是一类带有严格反馈结构的系统,这类系统中的非线性函数fi(·)至多包含系统中的前i个状态.然而,非严格反馈非线性系统中的非线性函数fi(·)是包含全部状态变量x=[x1,x2,…,xn]T的函数,这一特性无疑将增加虚拟控制器设计的难度.为解决上述问题,人们针对非严格反馈非线性系统展开了一系列的研究[10-14].在文献[13]中,通过对非线性函数进行假设解决了非严格反馈带来的困难,并且针对带有未知时滞的非严格反馈随机系统提出了一种自适应神经网络控制策略.不同的是,文献[14]移除了关于非线性函数的假设,利用模糊逻辑系统的结构特征克服了非严格反馈带来的困难.
随着网络控制系统的迅速发展,事件触发控制[15-18]作为一种节省网络通信资源的有效方法得到了广泛的研究.如文献[15]基于事件触发机制和命令滤波,讨论了一类随机非线性系统的追踪控制问题.
本文结合反步技术和事件触发机制,针对非严格反馈非线性系统提出一种自适应神经网络追踪控制策略.在控制设计的过程中,基于神经网络及其结构特征解决了系统中非线性函数和非严格反馈结构带来的问题.通过将反步技术、神经网络与事件触发机制相结合设计了一个自适应神经网络控制器,所设计的控制器不仅可以保证所有信号在闭环系统中有界,而且减少了控制器与执行器之间的传递次数,节约了通信资源.同时,通过排除芝诺现象证明了该方案的有效性.
1 问题陈述
考虑一类单输入单输出非严格反馈下的非线性系统:
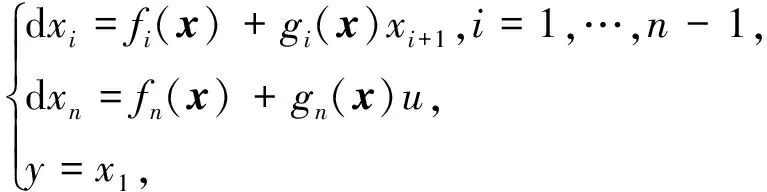
(1)

假设1[2]对于i=1,…,n,函数gi(x)的符号不变,存在已知常数g1和g2,使得
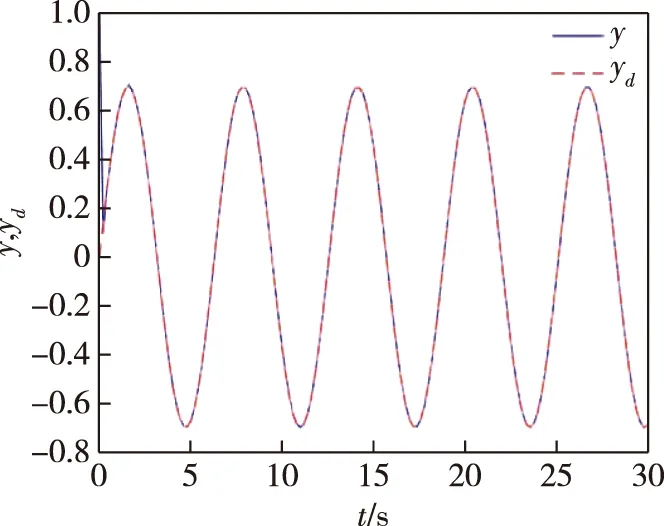
0 (2) 显然,式(2)表明gi(x)严格正或者严格负,因此可以假设gi(x)>0,∀x∈Rn. 控制目标:基于事件触发机制,利用神经网络自适应控制方法,使系统的输出y尽可能地跟踪到参考信号yd,且保证所有信号在闭环系统中是有界的. 为了更好地实现控制目标,下面给出一些预备知识. 引理1[1]对于任意的变量ξ∈R和常数ρ>0,有以下不等式成立: (3) 引理2[4]对∀t∈R+,令V(t)是一个连续函数并且V(0)有界.若有不等式 (4) 这里a1>0,a2>0是常数,则V(t)有界. 在本文中,径向基函数神经网络将会被用来逼近连续的非线性函数.径向基函数神经网络可被表达成如下形式: fnn(Z)=WTS(Z), (5) 其中Z∈ΩZ⊂Rq是输入向量,W=[w1,…,wl]T是权向量,l(>1)是径向基函数神经网络节点的数目,S(Z)=[s1(Z),…,sl(Z)]T是基函数向量且 这里μi=[μi1,μi2,…,μiq]T是接受域的中心且常数η>0是高斯函数的宽度. 式(5)表明如果f(·)在紧集ΩZ⊂Rq上是连续的,则对任意的精度ε>0,有一个径向基函数神经网络(5)使得 f(Z)=W*TS(Z)+δ(Z), 文化是一个群体在一定时期内形成的思想、理念、行为、风俗、习惯、代表人物,及由这个群体整体意识所辐射出来的一切活动。白银文化是明代中后期白银货币化后在闽东白银矿区及其左近地区出现的一种较为独特的货币拜物教,在此过程中辐射出来的白银是社会财富的直接化身,不仅成为流通物,而且成为物质世界和精神世界统辖者的现象。正如马克思所言“用物的形式掩盖了私人劳动的社会性质以及私人劳动者的社会关系”。[5]这就是货币的拜物教性质。 这里W*是理想的权向量且逼近误差δ(Z)满足|δ(Z)|≤ε. 通过反步设计法,构造一个针对系统(1)的自适应神经追踪控制器.首先,定义坐标变换如下: (6) 其中zi是虚拟状态追踪误差,αi是虚拟控制器. 在设计过程中,虚拟控制器和自适应律将会被设计为如下形式; (7) (8) 步骤1.由z1=x1-yd可得 (9) 给出如下李雅普诺夫函数为 (10) 通过联立式(9)和(10),可以得出: (11) 根据杨氏不等式有: (12) 将式(12)代入式(11)有 (13) 应用神经网络逼近φ1(X1),即: ‖δ1(X1)‖≤ε1,ε1>0. (14) 联立引理3以及式(3),式(14)可以被重新写为 (15) (16) 步骤i(i=2,…,n).由zi=xi-αi-1可得: (17) 其中 给出如下李雅普诺夫函数为 (18) 通过联立式(17)和(18),可以得出: (19) 根据杨氏不等式有: (20) 将式(20)代入式(19)有 (21) 应用神经网络逼近φi(Xi),即: ‖δi(Xi)‖≤εi,εi>0. (22) 与步骤1的处理方法相同,式(22)可以被重新写为 (23) (24) 步骤n.实际的控制器被设计为 (25) u(t)=ψ(tk),∀t∈[tk,tk+1). (26) 事件触发机制被设计为如下形式: tk+1=inf{t∈R||e(t)|≥d|u(t)|+r1}, (27) 由zn=xn-αn-1可得: (28) 其中, 给出如下李雅普诺夫函数为 (29) 通过联立式(28)和(29),可以得出: (30) 利用神经网络逼近φn(Xn),即: ‖δn(Xn)‖≤εn,εn>0. (31) 应用与前面相同的处理方法,式(31)可以被重新写为 (32) 根据u(t)的定义以及引理1,有以下不等式成立: zngn(x)αn+0.557κ. (33) 由杨氏不等式,可得: (34) (35) (36) 因此,由式(36)和引理2可以得出V(t)是有界的,且有: (37) 接下来,通过排除芝诺现象证明所提出的事件触发机制的可行性. 定理2考虑非严格反馈非线性系统(1)、虚拟控制器(7)、实际控制器(26)和自适应率(8),在假设1、假设2以及时间触发机制(27)的条件下,存在一个正常数t*,使得∀k∈Z+,{tk+1-tk}≥t*,进而芝诺现象被排除. 这一部分,将给出一个例子证明所提出方案的有效性.考虑下面的非严格反馈非线性系统: 自适应律被设计为 图1 输出y和参考信号yd的轨迹Fig.1 Trajectories of output y and reference signals yd 图2 追踪误差z1的轨迹Fig.2 Trajectory of tracking error z1 图3 状态x1和x2的轨迹Fig.3 Trajectories of states x1 and x2 图4 自适应参数和的轨迹Fig.4 Trajectories of adaptive parameters 图5 事件触发控制器uFig.5 Trajectory of event-triggered controller u 图6 触发时间的间隔tk+1-tk Fig.6 Time interval of triggering tk+1-tk 本文研究了一类非严格反馈非线性系统的自适应神经网络追踪控制问题.利用反步技术和神经网络逼近,设计了一个基于事件触发的自适应神经网络控制器,使闭环系统的所有信号有界.同时,所提出的事件触发机制减少了控制器与执行器之间的传递次数,并且避免了芝诺现象.所给出的仿真实例证明了该方法的有效性.
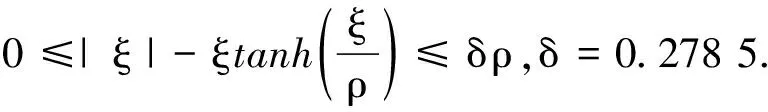
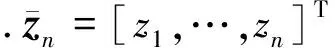

2 自适应神经网络控制设计







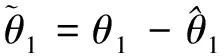

























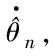
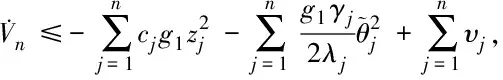
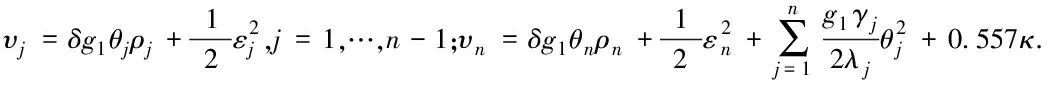
3 稳定性分析
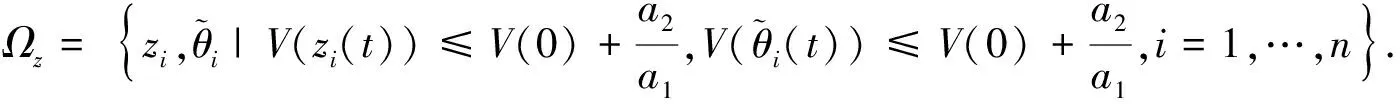
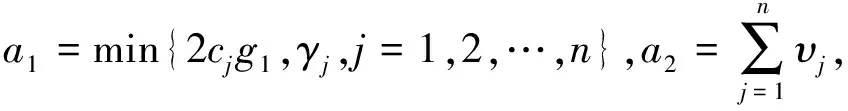

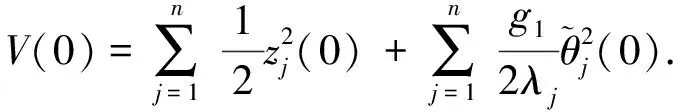
4 可行性分析

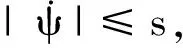
5 仿真实例






6 结论

