基于组合赋权的台阶爆破效果灰聚类评估模型*

杜承磊，周传波，王凤喜，刘 磊，殷 欣，陈仕钞

(1.中国地质大学(武汉) 工程学院，武汉 430074；2.中铁十六局集团第三工程有限公司，湖州 313000；3.武汉大学 土木建筑工程学院，武汉 430072)

随着爆破技术的发展，台阶爆破已广泛应用于露天矿山、铁路、公路以及水利水电等多个工程建设领域，其技术水平的高低决定了爆破生成的安全、质量和成本，因此在实际爆破工程中，准确、合理的对台阶爆破效果进行评价，寻找出最优的台阶爆破技术方案是十分必要的[1,2]。

在台阶爆破生产中，爆破效果的评价是一个重要环节，根据一系列的评价指标，结合工程概况和相关爆破要求，对每一次爆破效果进行评估，找出其中的优点和不足，进而对爆破技术进行优化，使各项指标达到最优。近年来，学者们尝试用不同的方法对爆破效果进行综合评价。王长友等基于BP神经网络的基本原理，从岩石力学性质、周边爆破参数两方面建立爆破效果BP神经网络模型[3]。韩新平等选取大块率、高尾矿率、根底等多指标，建立层次模糊综合评价模型，得出该矿最佳爆破方案[4]。赵国彦、黄治成等利用层次分析法与模糊综合评价相结合的综合评价模型对井下中深孔爆破进行效果评价[5]。胡新华等针对传统灰色关联分析模型权重分配主观性大，综合灰色关联理论和层次分析法，建立评价模型[6]。陶铁军等针对爆破效果因素指标不确定性问题，建立未确知测度的爆破效果综合评价模型，结合某露天铁矿深孔台阶爆破实际情况，基于未确知测度理论进行效果评判[7]。随着研究的不断深入，在采取不同的评价方法结合指标进行爆破效果综合评价时，指标权重的确定仍存在一些局限性。灰色关联分析、模糊数学分析、层次分析法等在确定指标权重时主观性较大，易受专家经验限制；未确知测度理论需专家经验作为知识补充，评价模型也存在主观误判性；BP神经网络模型结构复杂，受样本容量的影响；熵权法存在对指标的差异度敏感性较大的问题[8]。

为合理确定台阶爆破效果评价指标权重，利用层次分析法和CRITIC相结合的赋权方法，将灰色聚类评估模型引入台阶爆破效果评价中。该模型通过混合中心点三角白化权函数，对灰色聚类法进行优化，并基于离差平方和最大的原则将主、客观权重相结合得到综合权重。研究结果表明:该模型的评价结果能客观反映台阶爆破效果的现场情况，为台阶爆破效果评价提供了一种新途径。

1 灰色聚类评估模型

灰色聚类是利用灰色关联矩阵或灰色白化权函数将指标(对象)聚集分层成若干个类别的评估方法，是灰色系统理论的重要组成部分，它根据不同聚类指标所具有的白化权函数将聚类对象按已划分的灰类进行归纳，来判断该聚类对象的类别[9]。

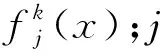
(1)

使用灰色聚类法时，需考虑评价指标数据的特点，避免白化权函数的多重交叉及不规范性，构造适用于台阶爆破各评价指标的中心点白化权函数，计算步骤如下：

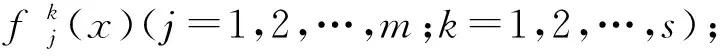
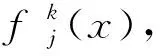
(4)判断矿山爆破对象i属于灰类k*的关系式满足

(2)

2 组合赋权

2.1 层次分析法

层次分析法(AHP)是20世纪70年代美国著名运筹学家Saaty提出的一种多准则决策方法[10]。层次分析法具有解决复杂层次结构的多目标决策问题能力。该方法简单实用、易于计算分析，但不能为决策提供新方案，在构造比较判断矩阵时受设计人员主观判断的影响，不够客观全面。运用层次分析法确定权重的步骤如下。

建立判断矩阵。判断矩阵中的元素表示的是同一层次指标之间的相对重要性。设判断矩阵为R，bij为指标bi较指标bj的重要性比例标度，在指标进行两两比较时，采用1～9标度法，则判断矩阵的基本形式为

式中：n是指标数目,bij>0;bij=1/bji;bii=1。

(1)计算各指标相对权重。权重计算的方法有两种，即几何平均法(根法)和规范列平均法(和法)，本文采用几何平均法，求出判断矩阵的最大特征值λmax，所对应的特征向量为W，对该向量进行归一化处理得到每个指标相应的权重。

(2)一致性检验。为提高指标权重的科学性，在求得最大特征根λmax后，相继计算一致性指标Ci和一致性比例CR，相关公式为

(3)

(4)

式中:n为判断矩阵阶数，当CR<0.1时，判断矩阵具有良好的一致性，随机性一致表如表1所示。

表 1 随机一致性指标赋值标准Table 1 Random consistency index assignment criteria

2.2 CRITIC赋值法

CRITIC法是由Diakoulaki在1995年提出的一种客观权重赋权法，其核心思想是利用指标的辨别力和指标间的冲突性来确定各指标权重[11,12]。首先，指标的辨别力是指同一指标在不同样本中取值的范围，反映了指标所含信息量的大小，用标准差来度量指标的辨别力，标准差越大，说明其辨别力越强，所含信息量越多，相应的指标的权重越大；反之，标准差越小，说明其辨别力越弱，所含信息量越小，相应的指标的权重越小。其次，指标的冲突性是指各指标间相关性的大小，一般用相关系数来度量指标冲突性的大小，若指标间所含重复信息越多，则指标冲突性越小，相关系数越大，对应的指标权重就越小。其主要计算步骤可归纳如下：

(1)建立原始数据矩阵A=(aij)m×n

(2)对原始数据进行标准化处理

对属性值越大越好的效益型指标有

(5)

对属性值越小越好的成本型指标有

(6)

(3)计算第j指标与其他指标的冲突性量化指标

(7)

Pj=σjRj,j=1,2,…,n

(8)

式中：rij为评价指标i和j之间的相关系数；σj为第j指标的标准差；Pj为第j评价指标所包含的信息量，Pj越大，包含信息量越大，该指标的相对重要性越大。

(4)计算各指标权重

(9)

2.3 基于离差平方和的最优组合赋权

层次分析法是根据评价者的主观经验来确定指标权重，CRITIC赋权法则是依据评价对象的测量数据来确定权重，故将主客观权重相结合可以计算出指标的组合权重，使指标赋权满足主观和客观的一致性。基于离差平方和最大的最优组合赋权方法，计算主、客观权重在组合权重中的比重，使评价对象的总离差平方和最大[13,14]。

针对台阶爆破效果评价问题，假设n个指标有s种赋权方法对其赋值，设第k种赋权方法的权向量值为

Wk=(w1k,w2k,…,wnk)T,k=1,2,…,s

(10)

式中：wik≥0,∑wik=1,k=1,2,…,s,j=1,2,…,n。

结合组合赋权方法的特点可得

Wc=θ1W1+θ2W2+…,θsWs

(11)

式中：Wc为组合赋权系数向量；θ1,θ2,…,θs为组合系数，k=1,2,…,s。

为使m个评价对象的总离差平方和达到最大，构造如下目标函数

(12)

若令矩阵Y1为

可知Y1为n阶对称方阵，则目标函数(JWc)可表示为

(13)

要求出组合权向量Wc，由式(11)知需求出系数向量Θ即可,于是基于离差平方和的最优组合赋权即为如下的优化问题

maxF(Θ)=ΘTWTY1WΘ

(14)

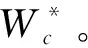
(15)

3 基于组合赋权的台阶爆破效果灰聚类评估模型

3.1 台阶爆破效果评价指标

台阶爆破效果评价指标的确定需全面考虑爆破质量、效率以及经济等因素的影响。评价指标过多，会使评价过程复杂化，而评价指标过少，又不能全面客观的台阶爆破效果，所以评价指标应具有较好的代表性，还易于获取数据。参考相关台阶爆破效果评价的研究文献[1]、[2]、[7]，根据台阶爆破的特点，选取6项因素作为台阶爆破效果的综合评价指标，分别用D1～D6表示，即大块率D1、松散系数D2、根底率D3、后裂距离D4、振动速度D5、飞散距离D6。其中松散系数、根底率、后裂距离、振动速度、飞散距离采用实测值进行评价，对大块率采用半定量化的方法进行取值，将大块率定性分为五个等级，依次对大块多，需要进行大量二次粉碎，赋值为1；大块较多，需要进行少量二次粉碎，赋值为2；大块一般，个别需进行二次粉碎，赋值为3；大块较少，可不进行二次粉碎，赋值为4；无，赋值5；建立指标等级分级标准(见表2)。

用于台阶爆破效果评价的聚类指标数m=6，可化分的台阶爆破灰类数s=5，各灰类对应的台阶爆破效果评价等级依次划分为台阶爆破效果很好(k=1)、爆破效果较好(k=2)、爆破效果一般(k=3)、爆破效果较差(k=4)、爆破效果差(k=5)。

3.2 构造改进的三角白化权函数

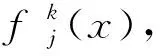
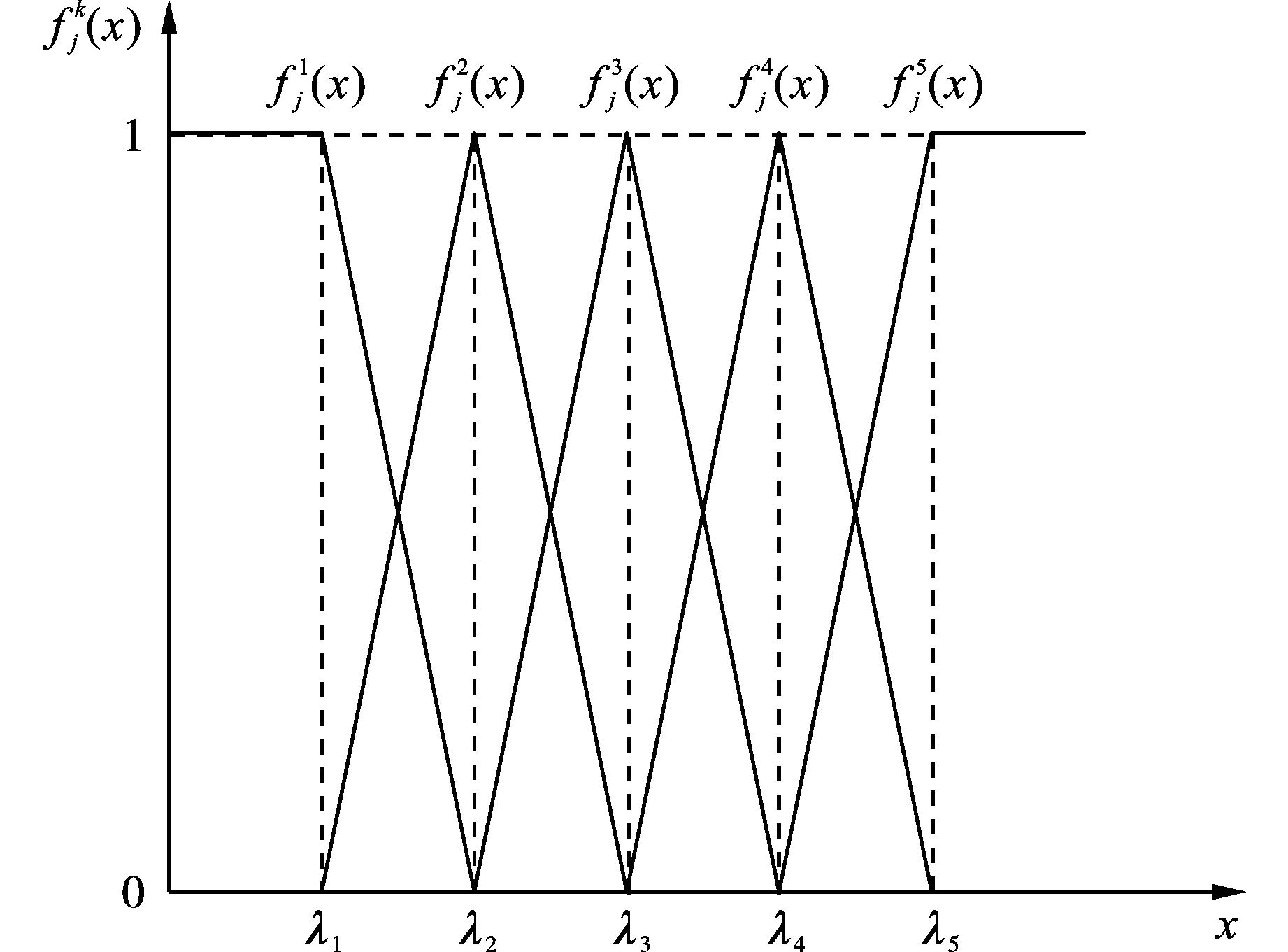
图 1 混合中心点三角白化权函数Fig. 1 Mixed center triangle whitening weight function

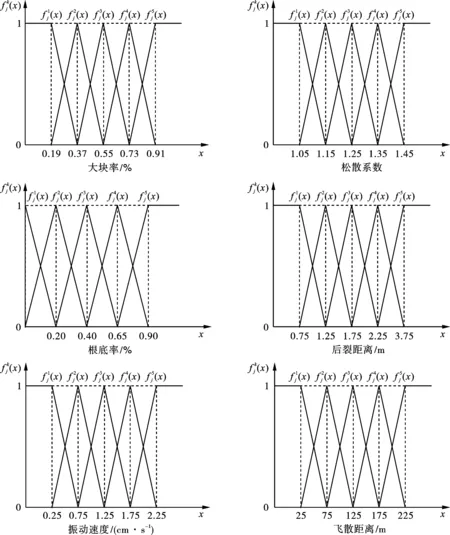
图 2 各指标三角白化权函数Fig. 2 Triangle whitening weight function of each index

(16)

(17)

(18)

4 工程应用

工程位于遵义市洪水台，属溶蚀盆地，覆盖层厚薄不均，含有泥夹石构造，节理裂隙发育，以中风化石灰岩为主，岩石硬度系数f为6.0～10.0，部分地区软弱夹层岩质呈砂石状。为了检验基于离差平方和最优组合赋权的灰聚类评估模型在台阶爆破效果评价中的有效性和实用性，参考遵义市洪水台土石方平场工程的4次深孔台阶爆破资料(见表3)及各爆破效果指标监测数据(见表4)，利用组合赋权的灰聚类评估模型对台阶爆破效果进行评价，具体实现过程如图3所示。

表 3 4次台阶爆破参数Table 3 Blasting parameters of 4 steps

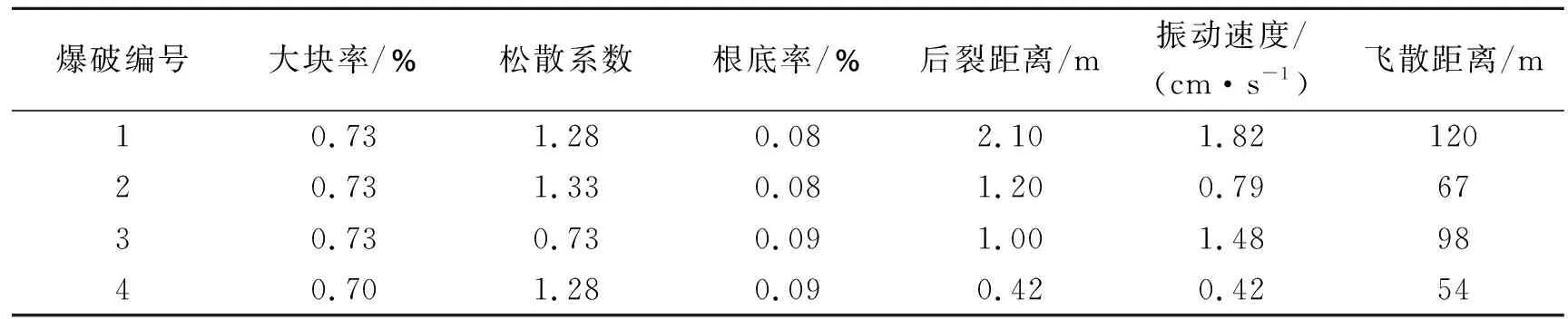
表 4 4次爆破效果及监控数据Table 4 Blasting effect and monitoring data of 4 times

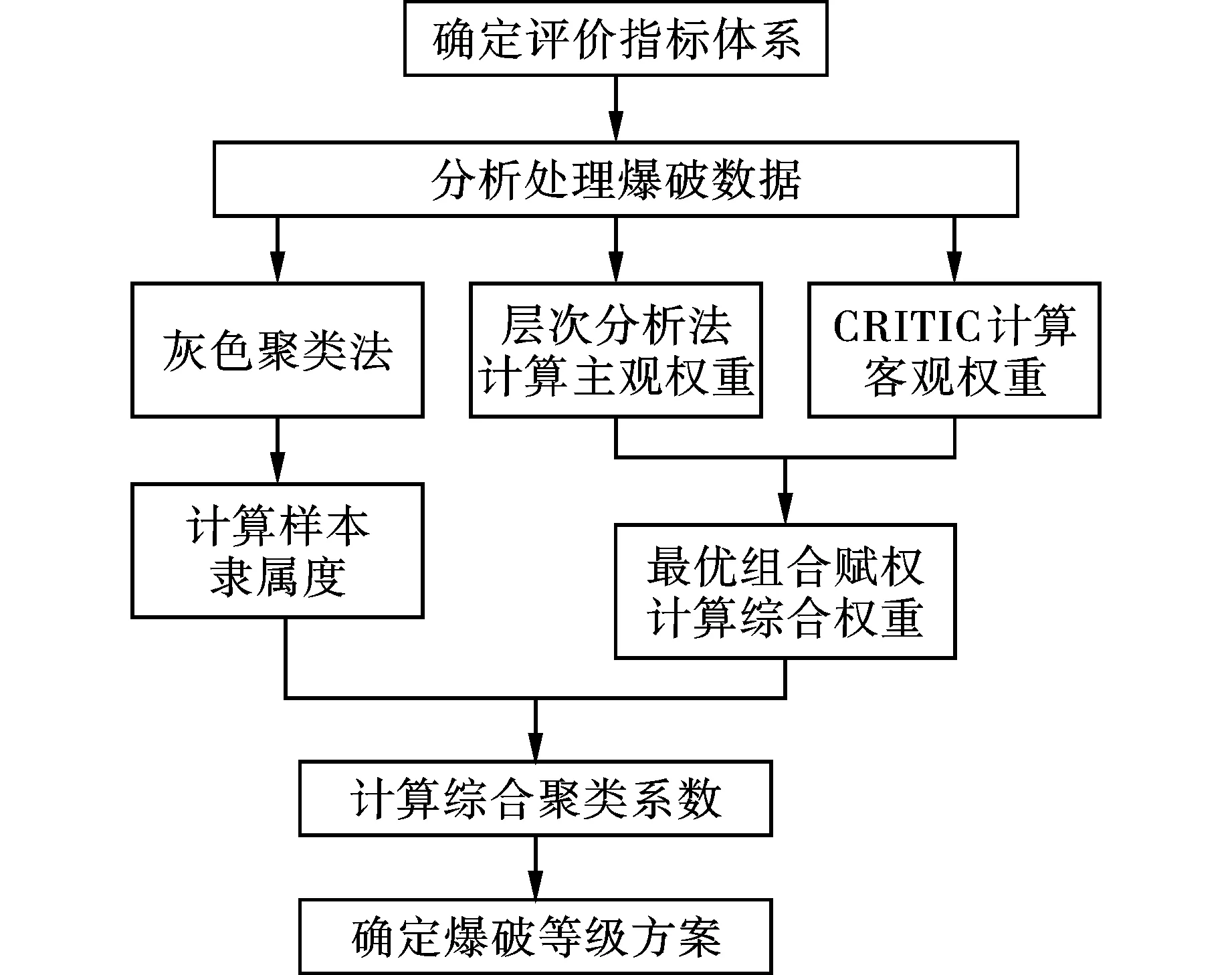
图 3 组合赋权灰聚类评估模型计算流程图Fig. 3 Calculation flow chart of combined weighted grey clustering evaluation model

4.1 组合赋权

(1)层次分析法计算主观权重

根据前述层次分析法，综合文献[15]和相关专家意见构建的判断矩阵为

经公式(3)、(4)可得判断矩阵R的最大特征值λmax=6.0966，最大特征值所对应的特征向量

CI=0.01932，RI=1.24，CR=0.01558<0.1

可知判断矩阵R满足一致性要求，归一化后可得主观权重向量

W1=(0.3072,0.1239,0.3072,0.0329,0.1624,0.0663)T

(2)CRITIC赋值法

将表3中数据进行标准化处理，代入公式(7)～(9)，进一步求得各评价指标的客观权重向量

W2=(0.230,0.094,0.284,0.134,0.128,0.130)T

(3)离差平方和确定组合权重

对洪水台土石方平场的4次爆破数据标准化处理后，根据Y1定义式有

由公式(10)、(11)构建两个权重系数向量组成的分块矩阵W=(W1,W2)

再根据公式(13)、(14)计算WTY1W得

最大特征根λmax=2.6541,其对应的单位化特征向量

Θ*=(0.6926,0.7213)

根据公式(15)求得单位化的组合权重

4.2 模型检验

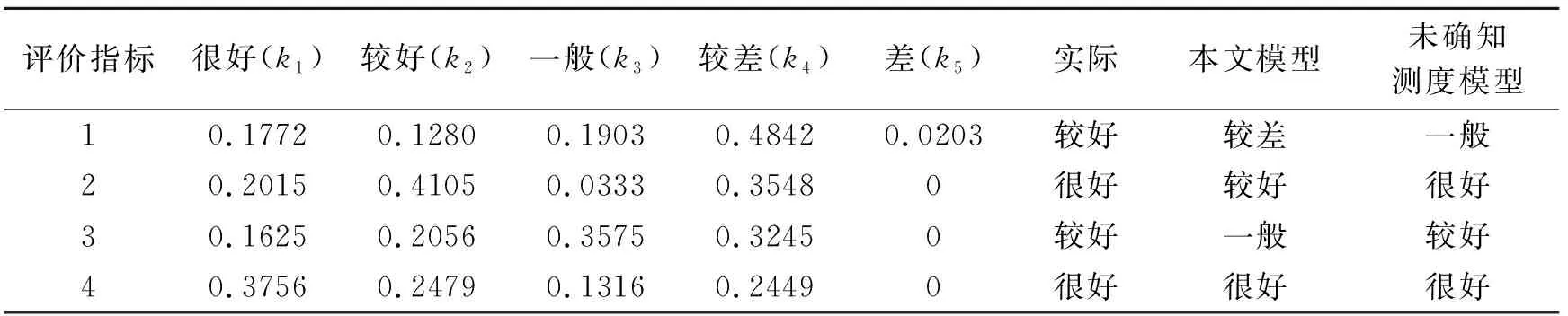
表 5 评价结果Table 5 Evaluation results评价指标

由表5知，4次台阶爆破效果评价等级依次为较差、较好、一般、很好。实际工程中，采用3.5 m孔距的爆破效果优于3.0 m孔距的爆破效果，逐孔起爆的爆破效果优于逐排起爆的爆破效果，因此建议采用3.5 m孔距的逐孔起爆方法。此模型评价结果与未确知测度模型评价结果基本一致，具有更高的精确度，说明采用灰聚类评估模型进行台阶爆破效果评价是合理的，具有一定的工程应用价值。

5 结论

(1)根据台阶爆破效果评价特点，考虑影响台阶爆破因数的重要性，选取大块率、松散系数、根底率、后裂距离、振动速度、飞散距离作为台阶爆破效果评估的评价指标。

(2)为了避免指标权重确定主观性大和数据差异性敏感较大的问题，采用CRITIC赋权法确定客观权重，并利用一种基于离差平方和的最优组合赋权方法将层析分析法确定的主观权重和CRITIC确定的客观权重相结合，使组合权重更全面、客观合理。

(3)台阶爆破效果评价是一个多因素影响的问题，灰色聚类评估模型在解决这类问题上具有显著的优越性。本文通过混合中心点三角白化权函数对灰聚类模型进行优化，建立台阶爆破效果评价的组合赋权-灰聚类模型，结合洪水台土石方平场工程的4次深孔台阶爆破实例表明：该模型计算结果与实际情况较吻合，具有一定的准确性和可靠性。