基于熵权值法修正AHP法的岩质深大基坑风险评价

宋 宸，张拥军，王观群

(青岛理工大学 青岛市 266033)

0 引言

近年来，随着城市化建设不断发展。用地紧张使城市中高层、超高层建筑数量在较短时间内得到快速提升。同时，人们将发展目标也瞄准到城市地下空间。地铁、地下停车场、地下商场等建筑物也在同一时间内大量兴建。这无疑对设计、施工到管理每一个环节都提出了更高要求。因此合理准确地对基坑稳定性进行评估也具有重要意义。

众多学者对基坑稳定性评估与安全风险评价方法进行研究。何锡兴等[1]通过对基坑施工过程中风险进行分析，建立风险评价模型，并对基坑安全进行评分定级；包小华等[2]利用模糊综合评价法，构造基坑风险评判矩阵，对基坑风险评价结果进行量化定级；涂建等[3]通过层次分析法对基坑四个方面共十一项指标进行评价，构建安全评价系统。赵博剑等[4]采用模糊数学评判法构建了隧道病害评价模型对隧道病害的多变性、复杂性特点加以表达，确定隧道安全等级，并与实际情况对照，证明其结果准确性。田林钢等[5]通过AHP法与熵权法确立主观权重与客观权重，通过多种方法进行结合建立风险评价模型，结合案例对每种方法所得结果进行对比，验证模型适用性。郭晋强等[6]利用熵权法对工程项目风险具体应用研究，并通过算例说明该方法的优越性和广阔的应用前景。刘波等[7]在WBS-RBS法基础上采用三角模糊数表示权重，构建判断矩阵。由于影响基坑稳定性因素众多，施工风险难以定量描述。将层次分析法与熵权值法相结合，可以得到一个综合权重，既避免了两者之间的矛盾，又弥补了各自的缺陷。根据熵权值法修正AHP法建立的专家自身权重数学模型，就可以对专家的评价水平进行评定。将其应用于基坑评价过程中，就可确定各专家评分结果的合理性及各专家意见的权重，以使评价指标权重的确定更加科学合理。

近年来，安全评价虽在基坑中应用已得到广泛应用，但由于岩质基坑有别于软土基坑，且岩体内部损伤和破裂是引发基坑失稳的重要原因。以往对基坑所建立安全评价都是以常规监测数据作为风险控制指标，各监测项目构建成风险评价体系，对基坑安全性做出评价。而常规基坑监测并没有加入对岩体内部损伤及破裂的监测，更没有进行定量分析。所以至今没有一套合适的岩质基坑安全评价方法。用熵权值法修正AHP法进行风险评价具有现实意义。

1 基于熵权值法修正AHP法的评价模型的建立

1.1 AHP法的指标权重确定

(1)确定递阶框架。确定对最终目标有影响的因子，分析因子间相互关联与隶属关系，分别自上而下确定目标层、准则层与标准层，建立递阶框架结构。依据递阶框架构造重要度评判矩阵。各层因子间进行重要性两两对比，按照1～9度标准对该层各指标重要度进行量化，具体准则如表1所示。

表1 1～9度标准表

假定目标层表示为C，准则层包含三个因子分别为C1、C2、C3。假设C1对于C2重要度为n12，则C2对于C1重要度为1/n12。其余因子间重要度可按同理求得。

(1)

(2)计算各因子权重。由线性代数矩阵理论可知，各因子权重值即为判断矩阵中特征向量W。特征向量所对应特征根为λmax。各因子权重值计算公式如下：

AW=λmaxW

(2)

其中判断矩阵特征向量即特征值计算方法众多，本文使用近似简易的和积法进行计算。

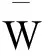
④得出权向量后计算评判矩阵最大特征根λmax。

(3)

(3)进行一致性检验。引入检验判断矩阵一致性的指标CI与修正系数RI的比值CR来检验评判者判断思维的一致性。其中RI取值参照表2所示。

表2 CR取值参照表

(4)

(5)

若CR<0.1，则判断矩阵具有满意的一致性，否则，就需要调整判断矩阵的最初取值，直至符合一致性为止。

同理，重复上述步骤即可得到s位专家对第n个因素指标确定的权重。最终得到权重矩阵W。

1.2 基于熵权值法的指标权重的修正

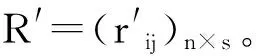
(6)

(2)对标准化矩阵按式(7)进行归一化处理，得到归一化矩阵。

(7)

(8)

(4)根据式(9)确定第i个因素的熵权值。

(9)

(5)对AHP法所求权重与熵权值法所求权值进行耦合。

Qi=eiwi+(1-ei)Hi

(10)

1.3 基于模糊理论确定目标层风险等级

选取S名专家按照评价集V中评判准则对指标层n个指标进行打分。通过式(11)对评判结果进行处理，得到指标层各因子隶属度，建立模糊关系矩阵Mi。

(11)

指标层综合权重Qi与二级模糊关系矩阵Mi相乘可得到一级模糊关系矩阵M。同理可知，准则层综合权重Q与一级模糊关系矩阵M相乘得到目标层综合健康评价结果，通过加权平均数法对目标层综合健康评价结果进行处理。其对应的安全等级即为目标所处安全等级。

2 工程案例分析

鞍山路站为青岛地铁4号线工程第8座车站。车站位于鞍山路与山东路交叉口西北角，与地铁8号线车站采用“L”型换乘；鞍山路换乘车站其深度达到了37.8m、面积超过1万平方米且为分段分区域施工典型特征，车站围护结构设计采用钢管桩+预应力锚索(锚杆)复合支护体系，采用基坑内排水，是目前青岛地铁车站最大的基坑施工工程。基坑下部属于岩质基坑，紧邻小学、居住区及高架桥，爆破震动会对周边环境造成影响。在基坑开挖影响范围内，有若干条污水管线、天然管线及通信管线等。鞍山路站位处有规划既有杭鞍快速高架桥与山东路高架桥互通立交桥，此规划互通立交桥对鞍山路站设计有重要影响。

通过对现场勘察及对专家评审意见的听取，除基坑变形、锚索轴力、地下管线变形、周边建筑变形、坑外道路沉降、车辆荷载、底部隆起等常规监测指标外加入了针对岩质基坑确定岩体内部损伤的微震等级、微震频率、土体压力三项指标。最终确定该岩质基坑风险评价模型指标层共11个因子隶属3个准则层因子。建立岩质基坑风险评价体系，如图1所示。

图1 基坑风险评价体系

2.1 AHP法指标权重的确定

在实际工程背景下，由于专家对各因子间重要性评判差距并不大，对最终相对权重值确定影响并不大。因此仅选取三名专家对各层因子间进行重要性两两对比，按照1～9度标准对该层各指标重要度进行量化，建立重要度关系矩阵。以专家1针对准则层对于目标层重要度评判为例计算说明并进行一致性检验。准则层对于目标层关系矩阵及权重如表3所示。

表3 第一层评价指标Ci对于目标层C的评判矩阵及相对权重值(专家1)

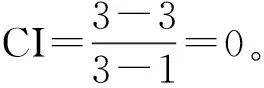
同理可得其他专家对各层评判指标评判结果。三名专家所给准则层权重及平均值，结果如表4所示。

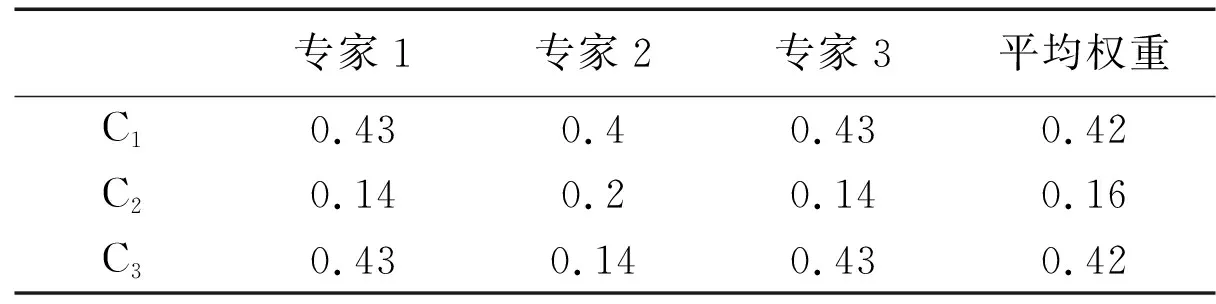
表4 第一层评价指标Ci对于目标层C的主观权重汇总

三名专家对指标层所给权重及平均权重如表5所示。

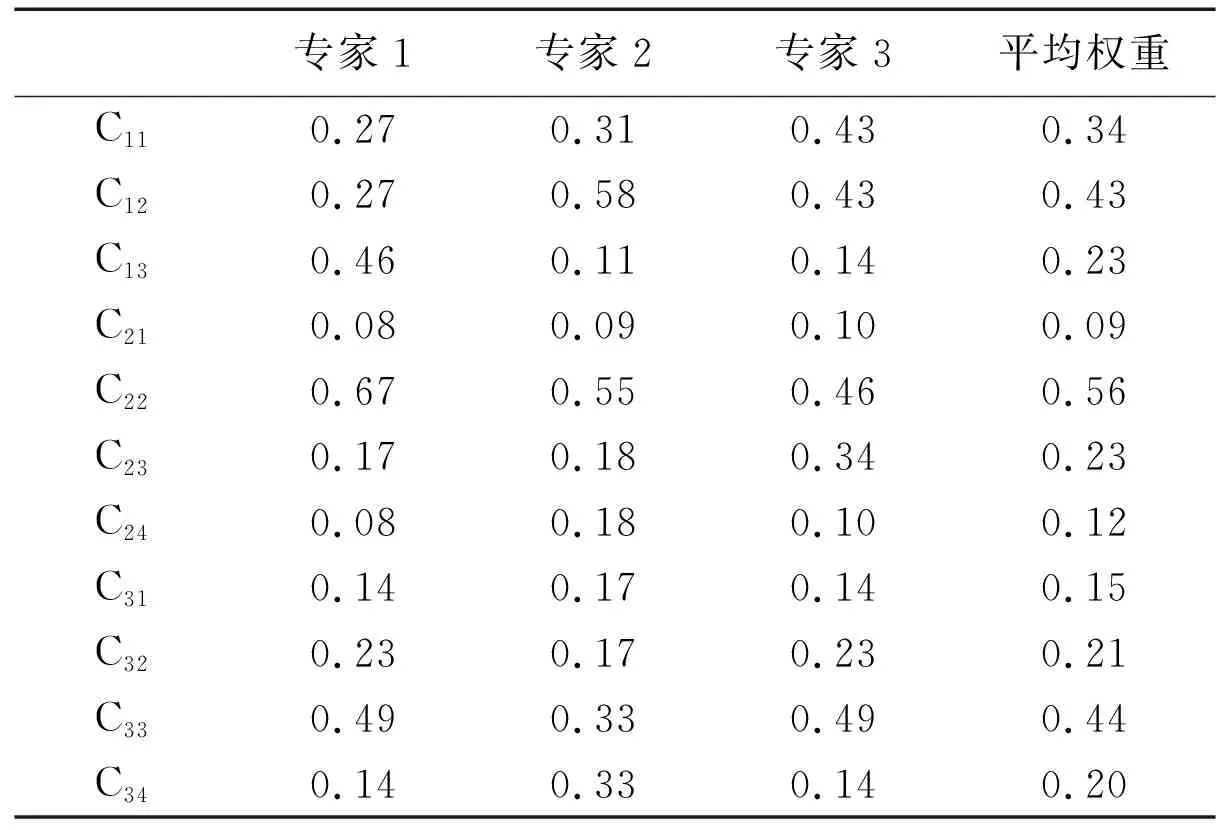
表5 第二层评价指标Cij对于准则层Ci的主观权重汇总

准则层相对于目标层权重向量为W=(0.42,0.16,0.42)T;标准层相对于准则层权重向量为W1=(0.34,0.43,0.23)T;W2=(0.09,0.56,0.23,0.12)T;W3=(0.15,0.21,0.44,0.20)T。

2.2 熵权值法对综合权重的修正

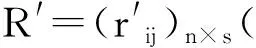
通过对原始数据矩阵标准化、归一化处理，按照式(8)、式(9)计算可得到各指标因子熵值与熵权值。结果见表6。

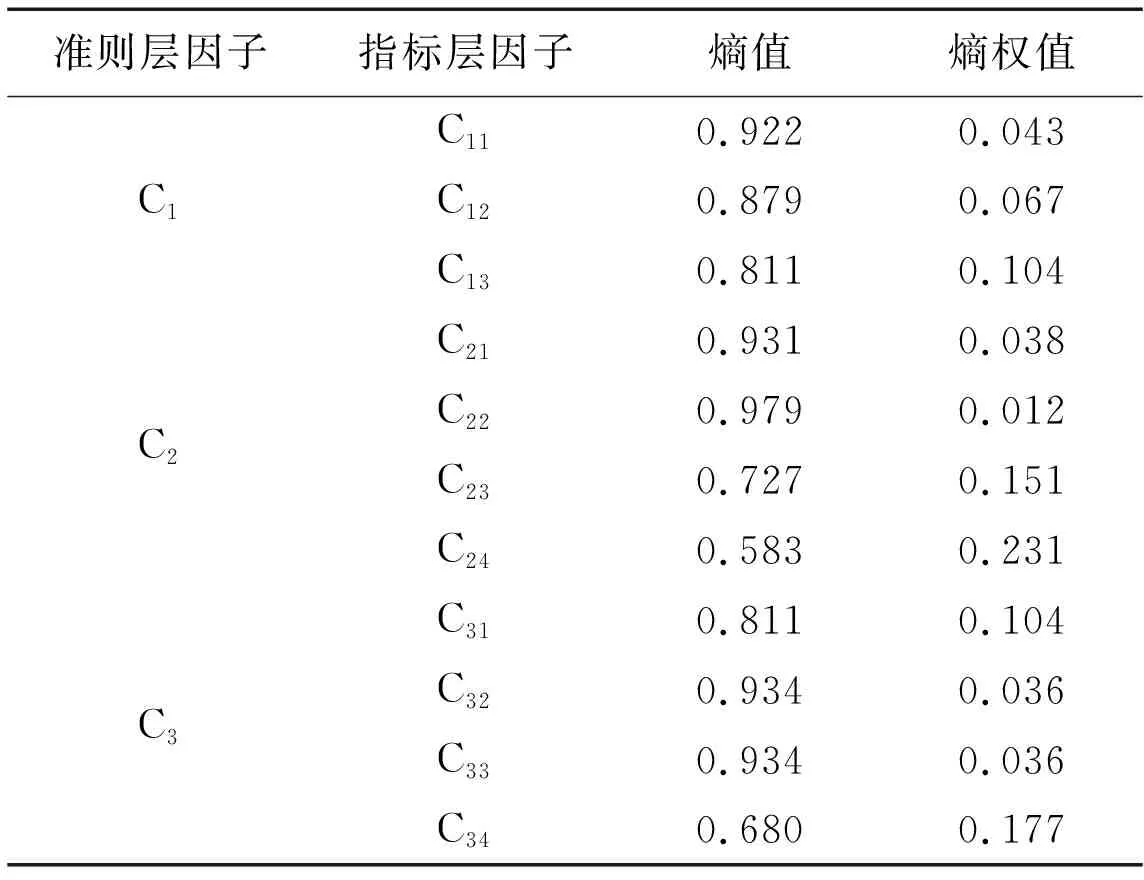
表6 各风险因子熵值与熵权值

利用式(10)对AHP法确定主观权重与熵权值法确定客观权重进行耦合，最终确定各指标因子综合权重。结果如表7所示。

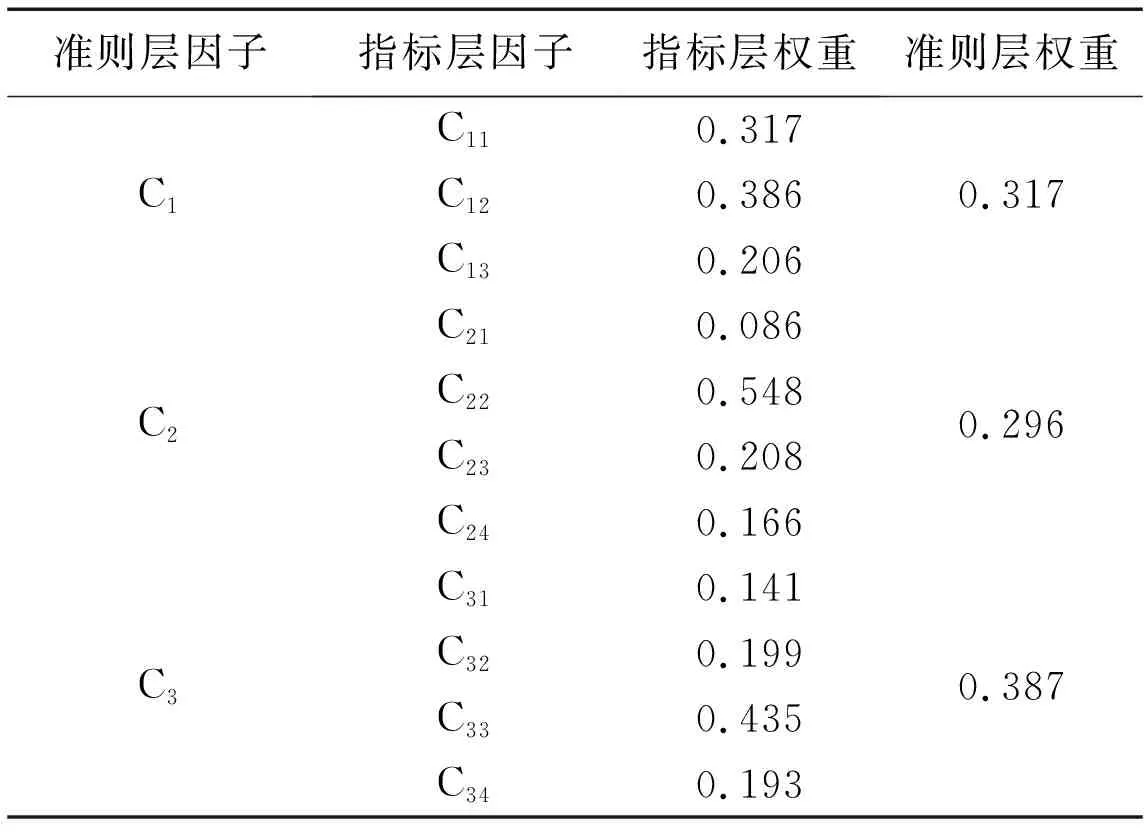
表7 各风险因子综合权重

2.3 基坑风险等级的确定

按照10名专家对每一评价指标进行打分构建的原始数据矩阵通过公式(11)可得评价因子C11隶属度分别为0.1、0.7、0.2、0。因此得到评价因子C11对评价集V的隶属向量为R=(0.1,0.7,0.2,0)。同理可得指标层其他因子隶属度向量。R12=(0.2,0.6,0.2,0)；R13=(0,0.6,0.4,0)；R21=(0.1,0.8,0.1,0)；R22=(0.3,0.7,0,0)；R23=(0,0.6,0.3,0.1)；R24=(0,0.4,0.6,0)；R31=(0,0.6,0.4,0)；R32=(0.2,0.7,0.1,0)；R33=(0.3,0.6,0.1,0)；R34=(0,0.5,0.5,0)。

准则层模糊综合评价：Si=Qi×Ri。

目标层模糊综合评价：

基坑安全风险评价分值F=0.157×4+0.623×3+0.218×2+0.006×1=2.939，由于3.5>F>2.5，故安全等级为Ⅱ级安全状态。

3 结论

深基坑安全性受多种因素影响，本案例引入微震技术对岩体内部破裂损伤进行定位与定级，与现场常规监测手段对照。所得结果反馈施工，对施工人员提供决策依据，早做预防，降低风险发生概率。该案例工程位于市区繁华地段，紧邻居民楼、小学及高架桥，周边管线密布，开挖深度较大。施工难度较大，对施工过程控制严格。由AHP法专家主观所给权重与熵权修正法所得客观权重有所出入，但差别不大，所以最终修正后所得误差结果较小。所得基坑安全等级为安全状态，与实际工程相符，体现出模型可行性。

本文虽然对工程项目安全评估提供一些有益理论，但仍有如下不足需要提高：

(1)在确定指标层评价因子时，考虑因素不够全面。所以最终所得结论不能排除其他因素影响。

(2)AHP法两两对比重要性程度过程受专家主观性影响较大，若选择评判因子过多，会导致多因子间重要性矛盾，导致一致性检验不符合要求，所花时间精力较多但效率不高。