红花香椿单木及林分材积生长率模型研究

林俊平

摘 要：为解决红花香椿单木及林分材积生长率表缺乏的问题，通过收集样木、样地数据处理、备选模型求解、模型选优、模型优化等思路和过程，建立了红花香椿单木及林分材积生长率模型。经TOPSIS法模型选优显示，单木和林分材积生长率最佳模型均为[P=a0D-a2t-a1];利用免疫进化算法（IEA）进一步优化了模型参数，提高了模型预估精度，并据此编制了红花香椿单木及林分材积生长率表。

关键词：红花香椿;单木材积生长率;林分材积生长率;林业数表模型

中图分类号 S792.32;S758文献标识码 A文章编号 1007-7731（2021）05-0040-04

森林生长量确定的较好方法为材积生长率模型[1]。通过建立以年龄（t）和胸径（D）为自变量、材积生长率为因变量的生长量模型能快速计算出不同年龄、胸径的材积生长率，对林业生产实践上确定森林采伐量具有重要参考意义[2-5]。红花香椿（Toona fargesii A. Chevalier），楝科香椿属植物，是福建省主要栽培珍贵树种，于1956年发现于福建南靖的植物新种。福建是红花香椿的模式产地，从闽南至闽北均有原生分布。国内外相关研究文献检索表明，至今鲜有红花香椿的研究报道。研制红花香椿单木及林分材积生长率模型，编制单木及林分材积生长率表，具有重要的实践意义[6，7]。截至目前，有学者对福建古田县、福建省尤溪国有林场等地区分布的杉木等树种单木或林分材积生长率表进行了编制[8，9]，而关于红花香椿材积生长率表尚缺乏。基于此，本研究在红花香椿分布区收集样木、样地数据，依据已有的研究理论，建立红花香椿单木及林分材积生长率模型，编制单木及林分材积生长率表，为红花香椿生产实践提供理论依据。

1 材料与方法

1.1 试验概况 在红花香椿分布区布设不同林分年龄、生长良好、郁闭度0.4以上的红花香椿正方形样地，样地规格为25.82m×25.82m，并利用测高器、围径尺等工具进行每木调查，共收集86个样地。样地林分年龄最小10年、最大32年，胸径最小5.0cm、最大34.8cm，树高最低1.6m、最高27.9m，样地平均株数2057株/hm2。根据每木调查结果，结合采伐作业工作，樣地内采伐1～3株红花香椿标准木作为解析木进行解析，数据用于红花香椿材积生长率计算。

解析木按原木长的0.9、0.8、0.7、…、0.2、0.1截取5cm厚的圆盘，共收集了89株解析木数据，径阶分布为10cm以下、12～20、22～30、32～40cm。解析木的数据按式（1）计算红花香椿材积生长率（P）。计算后，绘制年龄为横轴、材积生长率为纵轴的散点图，剔除异常样本数据。经整理，用于建模的解析木数据为85株。

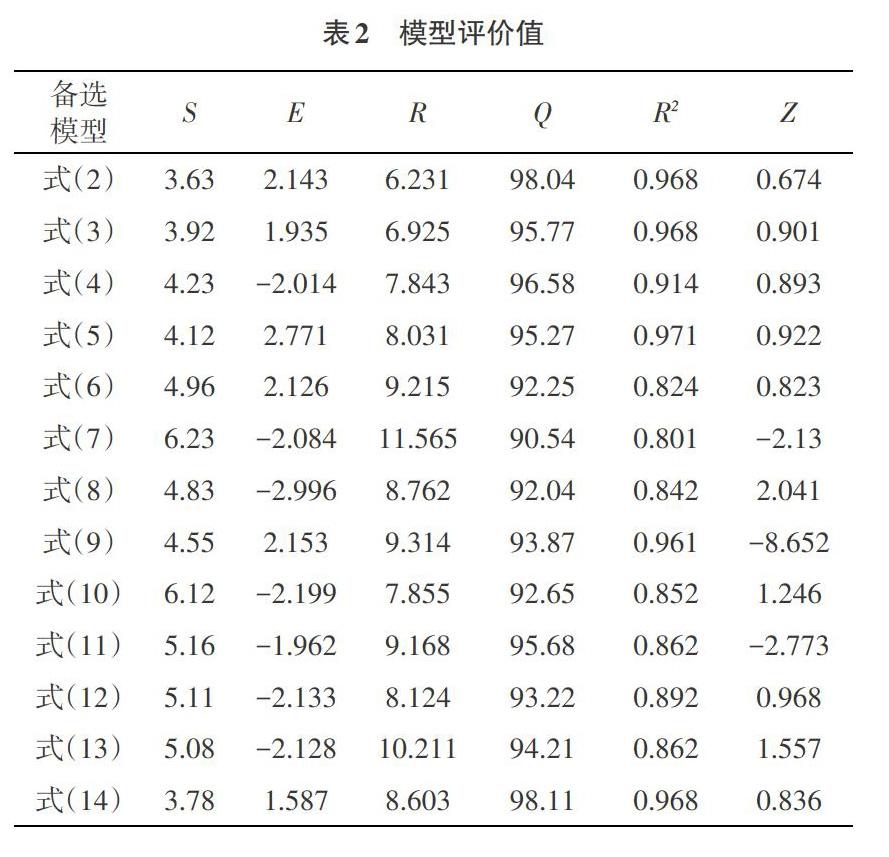
1.2 材积生长率模型 基于最优模型的建立原则，结合前人的研究[8，9]，选用17个常见的材积生长率方程作为红花香椿材积生长率的备选模型，并利用相关指数（R2）、剩余标准差（S）、总相对误差（Z）、平均系统误差（E）、平均相对误差绝对值（R）、预估数度（Q）等6个指标作为模型选优指标[10]评价模型的优劣。备选模型如下：

2 结果与分析

2.1 单木材积生长率模型

2.1.1 最优单木材积生长率模型 利用SPSS软件的线性、非线性拟合工具，将式（2）～（18）分别输入软件后，以最佳相关指数最大、拟合标准差最小为目标，经多次模型各参数初始值的给定和计算迭代，求解出备选模型参数（表1）。

2.1.2 模型优化处理 为能更好地描述红花香椿材积生长率规律，本研究在算法上作进一步调整，拟采用免疫进化算法（IEA）作进一步优化[11，12]。IEA是基于一种生物的免疫而开发的算法，主要公式如下[13]：

式中：Xt+1为子代的各个解;Xtbest为父代的最佳个体;St为父代的标准差;P（0，1）为符合标准正态分布的随机个体数;Sn+1为子代的标准差;B为标准差动态调整系数;n为进化的代数;N为所有进化代数。

经计算得到红花香椿材积生长率模型如式（21）所示，其剩余标准差2.25，与之前的3.63相比下降38%，说明结果有进一步的优化。

2.2 林分材积生长率模型 前人研究认为林分材积生长率的变化趋势与单木的一致，显示负指数型或“厂”型变化趋势。研究按照单木材积生长率选优思路，得到红花香椿林分材积生长率最佳模型为：

式中，PL为红花香椿林分材积生长率;[D]为红花香椿林分平均胸径;a0、a1、a2为待估算的模型参数。经免疫进化算法（IEA）估算，得到红花香椿林分材积生长率模型为：

经Excel对6个指标的计算，得到相关指数（R2）为0.958、剩余标准差（S）为5.744、总相对误差（Z）为2.074、平均系统误差（E）为3.256、平均相对误差绝对值（R）为8.241、预估数度（Q）为93.56。

2.3 模型检验与数表编制 为进一步说明红花香椿单木材积生长率模型和林分材积生长率模型的适用性，分别利用30个未参加建模的样本数据作为适用性检验材料。本次选用置信椭圆F检验、总相对误差（Z）、平均系统误差（E）、平均相对误差绝对值（R）、预估数度（Q）作为适用性评价指标。经计算得到红花香椿单木和林分材积生长率模型的适用性结果（表4）。

3 结论与讨论

本研究按照材料收集、数据处理、备选模型求解、模型选优、模型优化等思路和过程，建立了红花香椿单木及林分材积生长率模型。经过置信椭圆F检验、总相对误差（Z）、平均系统误差（E）、平均相对误差绝对值（R）、预估数度（Q）等指标检验，本次建立的红花香椿单木及林分材积生长率模型适用，可用于林业生产上统计红花香椿生长量。

研究发现，红花香椿单木和林分材积生长率的最佳模型均为[P=a0D-a2t-a1]，该模型与福建省现行的二元材积模型通式[V=a0Da1Ha2]相似。因此，该模型能反映出单木及林分材积的生长规律，即随着年龄（t）和胸径（D）的变大，材积生长率（P）逐渐减小，最终P越来越接近0，符合生物学特性，说明本研究建立的红花香椿单木及林分材积生长率模型具有一定的理论意义。以TOPSIS法为模型选优技术、免疫进化算法（IEA）为参数优化方法，进一步提高了红花香椿单木及林分材积生长率模型精度，可以更好地描述红花香椿单木及林分材积生长率变化规律。本次研究中，材积生长率参数是否会随着年龄（t）和胸径（D）的变化而发生变化，试验未作进一步分析，今后应增加该部分的研究，以完善研究结论的系统性和全面性。

参考文献

[1]张利军.森林生长量的测定[J].内蒙古林业调查设计，2015，38（3）：26-27.

[2]叶伟光.明溪县马尾松人工林单木材积生长率模型的研究[J].林业勘察设计，2019，39（3）：44-47.

[3]马炜，陈丽聪，王雪军，等.西藏主要天然林树种单木材积生长率模型[J].中南林业科技大学学报，2018，38（04）：40-45.

[4]刘雪惠，王海龙，温小荣，等.广西桂北马尾松不同起源单木和林分材积生长率模型研究[J].林业资源管理，2016（3）：54-60.

[5]陈利，王福生，管远保，等.湖南省杉木材积生长率模型研究[J].中南林业科技大学学报，2015，35（11）：49-54.

[6]伍汉斌，段爱国，张建国.杉木地理种源不同林龄生长变异及选择[J].林业科学，2019，55（10）：181-192.

[7]黄炜.南平市延平区杉木与福建柏混交林生长对比研究[J].福建热作科技，2019，44（3）：11-14.

[8]黄修麟.尤溪国有林场杉木人工林单木材积生长率表编制研究[J].林业勘察设计，2010（2）：8-11.

[9]程光明.杉木人工林材积生长率表编制的研究[J].福建林业科技，2006（3）：56-59.

[10]华伟平，丘甜，盖新敏，等.基于交叉建模检验的黄山松二元材积模型建模技术[J].武夷学院学报，2015，34（6）：13-17.

[11]万芳，原文林，黄强，等.基于免疫进化算法的粒子群算法在梯级水库优化调度中的应用[J].水力发电学报，2010（1）：202-206，212.

[12]梁晓龙，李祚泳，汪嘉杨.免疫进化捕食算法用于二维水质模型横向扩散系数优化[J].环境工程，2013（5）：136-138.

[13]施恭明，陈绍玲，江希钿，等.基于免疫进化算法的投影寻踪森林生态功能评价模型[J].福建林学院学报，2013（2）：142-145.

（责编：徐世红）