山谷地形对入射SV波地震反应分析

卓发成

(上海隧道工程股份有限公司, 上海 200023)

0 引言

强震动记录和震害调查以及理论研究表明[1-4],局部地形条件会对地震波的传播产生重要影响,使得地震动空间分布特征呈现显著的差异。目前研究地形效应的方法主要有强震动地形效应观测、解析法和数值模拟法[3]。地形效应观测依赖台阵的分布,解析法主要针对可使用简单参数能描述的模型[5-7],数值计算方法适用于对复杂场地的地震反应模拟,可以弥补解析法在求解复杂场地时存在的不足。目前常用的数值计算方法有:有限差分法[8]、边界元法[9]、谱元法[10-11]、有限元法[12-14]等。

其中,有限元法在处理计算模型的几何和物理条件上具有优势,因此运用最为广泛。刘晶波[12]运用有限元法结合修正的透射人工边界,研究了相邻凸起地形中地震波传播对地面运动的影响;荣棉水等[13]研究了两个相邻平台状凸起地形在不同入射角度的P波作用下频谱特性的影响分析;金丹丹等[15]利用ABAQUS软件研究典型复合地形场地对SH波的影响,结果表明,相邻地形对特定频段地震动放大效应与聚集效应比较明显,局部地形变化将引起地震动持时差异,且持时和输入地震动特性相关。

随着我国经济建设快速发展,大量的高速公路、大型水坝、长输电塔(线)等大型工程项目的涌现,多地貌单元复合场地的地震反应分析越来越受到重视。在我国《建筑抗震设计规范》[16]中也明确规定:对复杂地形或地形变化明显的建筑场地,应估计不利地段对设计地震动参数的放大作用。本文在显式有限元方法的基础上结合黏弹性人工边界研究了具有单一突出平台的山体地形和相邻山体地形对地表地震动特性的影响,并分析了相邻凸起之间距离变化对计算结果的影响。

1 计算模型及输入地震动

单一凸起山体地形和具有两个凸起山体地形的计算模型如图1所示。假设所有凸起平台宽度与高度均为R,大小为50 m,坡角均为45°,相邻凸起之间的距离为d,计算区域的宽和高均为250 m,所有模型均为均质、各向同性、线弹性介质,具体参数列于表1。由于实际地震动的频段往往较宽,为了研究频段内不同观测点地面运动的特性,入射地震波为垂直入射的SV波,其时程曲线及傅里叶幅值谱如图2所示。

图1 单一凸起与相邻凸起山体地形模型示意图Fig.1 Terrain models with single and adjacent hills

表1 模型介质参数

图2 输入地震动位移时程及傅里叶幅值谱Fig.2 Displacement time-history and its Fourier spectrum of incident earthquake wave

2 计算方法

2.1 集中质量显式有限元的内点计算方法

集中质量显式有限元的实质是根据当前时刻的节点运动方程求解下一时刻节点的运动,它不需要进行刚度、质量、阻尼阵的集成,这样整个计算只需要很小的高速存贮区,计算效率较高。尤其当一系列单元的刚度阵、质量阵、阻尼阵相同时,就不需要重复计算,效率更高。

对于内点,由动力平衡条件可建立运动方程:

(1)

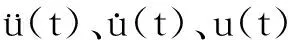
对于运动方程式(1),采用中心差分法得到逐步积分格式:

[M]{u(t+Δt)}=[M](2u(t)-{u(t-Δt)}-Δt2[K]{u(t)}-Δt[C]({u(t)}-

{u(t-Δt)}))+Δt2{F(t)}

(2)

2.2 黏弹性人工边界

刘晶波等[17]根据波动方程给出了二维黏弹性动力人工边界参数:

切向:

(3)

法向:

(4)

式中:Kbn、Kbt分别为法向与切向的弹簧系数;,r为散射源至人工边界点的距离,在场地反应中,一般将地表中心点假定为散射源;G为剪切模型;αT与αN为人工边界参数,本文中分为取值为0.5和1.0;Cbt、Cbn分别为法向与切向的阻尼系数,cS与cP分为S波和P波波速。

一致黏弹性人工边界单元的刚度矩阵为:

(5)

(6)

直接将式(5)、(6)的单元刚度以及阻尼矩阵组装到原结构整体刚度矩阵中,便可以完成黏弹性人工边界的施加。

2.3 方法验证

二维有限元模型计算尺寸为200 m×400 m,顶端为自由表面,单元网格尺寸为5 m×5 m。模型介质材料参数列于表1。在底部垂直向上入射x方向单位脉冲剪切位移波,入射波位移时程及其傅里叶幅值谱见图2。图3给出了基于黏弹性人工边界的显式有限元方法计算得到的模型底部、中部、顶部3个观测点的水平向位移时程曲线与理论解的比较。由图3可知,入射波由底部向上传播在自由地表发生反射,自由地表处的位移幅值为输入波幅值的两倍,下行波从底边界,没有发生反射现象。本文的计算结果与理论解吻合得很好,证明了本文计算方法的正确性和有效性。

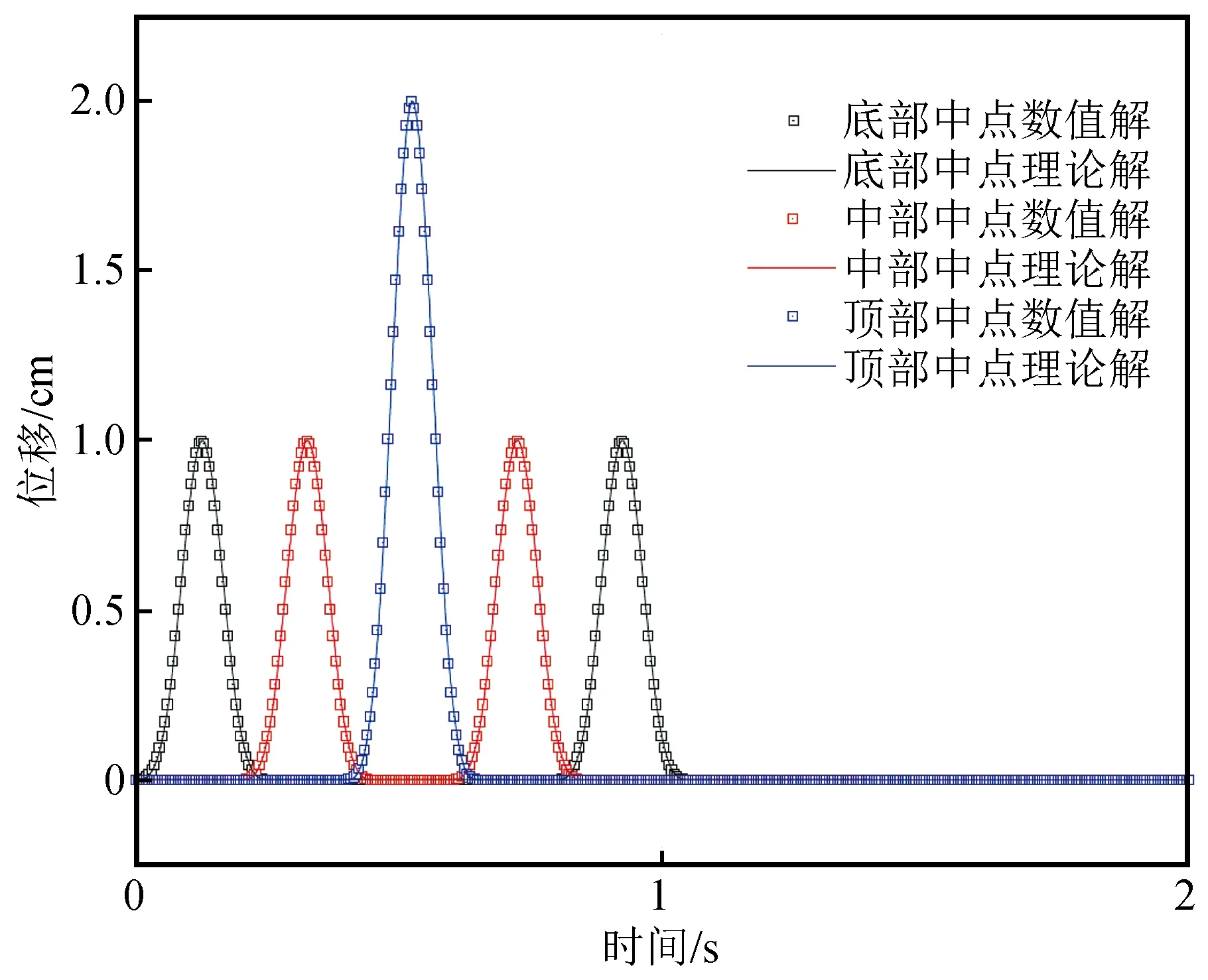
图3 数值计算结果与理论解比较Fig.3 Comparison of numerical results and the theoretical solution

3 凸起山体地形对地震动反应谱特性的影响

首先,以单一凸起山体地形模型为例分析山体地形对地表地震动特性的影响效应。图4为单一凸起山体地形模型在SV波垂直入射的情况下地表峰值位移(PGD)分布情况,从图4可以发现:(1) 由于单一凸起山体地形是以观测点1为中心的轴对称模型,且入射波为垂直入射的SV波,因此整个模型的PGD分布情况也呈现出对称形式;(2) 从山脚至山顶处的PGD逐渐增大,但是在山顶平台处的PGD出现了降低的趋势;(3) 地表同一监测点沿着x轴方向的反应较y轴方向更为强烈。可以初步判断局部凸起的山体地形的存在使得地表各点处的地震动发生了变化,主要表现在放大了山顶的地面运动,山腰和山脚处的地面运动有所减小。

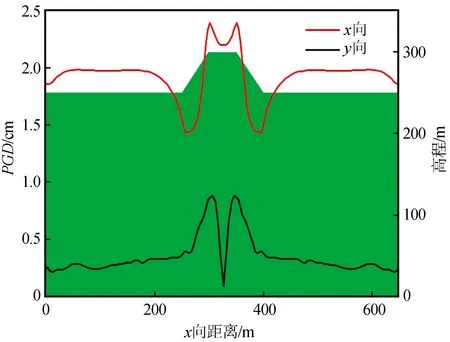
图4 单一突起山体模型地表PGD分布图Fig.4 Distribution of surface PGD of the model with single hill

为了进一步研究地形对地表运动的影响,图5给出了4个观测点沿水平方向的位移时程、位移傅氏谱及谱比。谱比为凸起山体地形条件下观测点的地震动位移傅氏谱与均匀半空间场地自由地表的地震动位移傅氏谱的比值。从图5中可以发现观测点1在2.5～8 Hz这一频段内的谱比略小于1,在0～2.5 Hz和8～10 Hz这两个频段的谱比大于1。观测点2在0～10 Hz整个频段内的谱比均大于1。观测点1和观测点2均在山顶处,但观测点1位于山顶平台处,表明相邻地形会对地震动的频谱产生放大作用。观测点3位于山腰处,在0～1.5 Hz和5.5～7.5 Hz这两个频段内的频谱幅值有所放大。观测点4位于脚处,其放大的频段范围最小。

以下为地震动输入一致的条件下,分析相邻凸起山体地形对地表地震动的影响定义ξ=d/R。图6给出了相邻凸起山体之间距离变化时地表PGD分布图,可以发现由于两个相邻的山体具有对称性,其地表PGD的分布也具有对称性,同时可以发现沿着x轴方向的PGD数值整体上大于沿着y轴方向的PGD数值,表明沿着地震动输入方向的地表反应较其他方向的反应更为强烈,这与单一凸起山体地形条件下模拟结果类似。

图7给出了相邻凸起山体之间距离改变时对地表4个观测点的PGD影响,4个观测点的位置如图1(b)所示。由图7可知当ξ逐渐增加时,观测点1、2和点3沿着x轴方向上变化趋势很小,但是位于山脚处的观测点4呈现出先增大后不变的趋势;当ξ为2时,这4个观测点PGD的变化趋势逐渐稳定,此时这4个观测点的PGD依次减小;在y轴方向上观测点1和观测点2呈现出逐渐减小的趋势,位于山峰处的观测点3和位于山脚处的观测点4都呈现出先增大后减小的变化趋势。当这4个观测点在y轴方向的PGD逐渐趋于稳定时位于上顶平台处观测点1的PGD值最小。同时可以发现,位移在山脚处的观测点4随着ξ改变时PGD在x轴和y轴方向上的改变是最大的,分别为16%和587.5%。

图5 单一突起山体模型地表不同观测点的位移时程、频谱及谱比Fig.5 The displacement time histories, frequency spectra, and spectrum ratio at differentobservation points derived from the model with single hill

为了进一步研究相邻凸起山体之间距离的变化对地表地震动的影响,图8给出了相邻凸起山体之间距离改时模型地表4个观测点的位移时程、频谱特性以及谱比的变化。可以发现这4个观测点的位移时程曲线变化不大,但是从位移频谱中可以发现随着ξ的改变,在1～4 Hz这一频段内的变化较为明显,但是每个观测点的卓越频谱并未发生改变。从谱比中可以发现,位移在山顶平台处的观测点1放大频段与单个凸起山体地形模型的计算结果相同,然而在7～10 Hz这一频段内的谱比值明显大于单个凸起山体地形模型的计算结果。观测点2、3和4各个频谱所对应的谱比值随着ξ的改变而改变,但ξ对放大频段的影响甚微。

4 讨论与结论

基于显式动力有限元计算方法和黏弹性人工边界处理方法,探讨了局部单一凸起及相邻凸起的山地地形在垂直输入SV波的情况下对地震动参数放大效应的影响。有如下结论:

(1) 地表地震动沿着输入地震动方向的影响比其他方向的影响更大;

(2) 局部凸起地形对地表地震动有放大效应,从山顶至山脚处放大趋势逐渐减小;

(3) 与单一凸起地形相比,相邻地形的存在对地表地震动的谱比曲线形状影响不大,但是随着相邻凸起之间距离的增加,其对PGD具有显著的影响(就本文所涉及的算例而言,位于山脚处观测点沿着地震动输入方向的PGD最大可达到单一凸起放大倍数的1.16倍)。

图6 相邻凸起山体之间距离变化时地表PGD分布图Fig.6 Distribution of surface PGD with different distance between adjacent hills

图7 相邻凸起山体之间距离对地表观测点的PGD影响Fig.7 Effect of different distance between adjacent hills on the surface PGD

因此,在对局部地形对场地地表地震动的影响进行分析时,应对这种相邻地形的动力相互作用效应对分析结果的影响加以重视。

图8 相邻凸起山体之间距离变化时模型地表不同观测点的位移时程、频谱及传递函数Fig.8 The displacement time histories, frequency spectra, and transfer functions at differentobservation points of the model with different distance between adjacent hills