有限信息环境下基于学习自动机的发电商竞价策略

贾乾罡，陈思捷，李亦言，2，严 正，徐澄科

（1. 上海交通大学电子信息与电气工程学院，上海市200240；2. 北卡罗来纳州立大学电子与计算机科学系，罗利市27695，美国）

0 引言

自2015 年启动新一轮电力体制改革以来，中国电力市场化进程在各省快速推进。电力中长期交易趋于成熟，现货市场架构及市场机制设计逐渐完善。在这种情况下，市场成员的参与策略具有了实际的研究价值。

电力市场通常被认为是典型的不完全竞争市场或寡头垄断市场。在该类市场中，发电商有充分的动机开展策略性报价以提高自身收益［1］。现有对发电商投标策略的研究可大致分为以下3 类。①发电商通过预测下一阶段市场出清电价及负荷，从而制定相应的投标策略［2-4］。该类方法仅适用于价格接受型（price taker）发电商，即假定他们自身的投标策略对市场价格无影响。②通过建立市场的博弈均衡模型以得到自身的最优投标策略［5-6］。该类方法要求发电商能够获取全部的市场信息，在实际应用中存在难度。③发电商通过研究对手的报价行为并对其建模，估计对手的报价策略，从而针对性地优化自身的策略［7-8］。这类研究通常需要假设对手的行为服从某种特定分布。事实上，发电商可获得的外部市场环境信息、竞争对手信息往往较为有限，尤其是在新兴市场中可参考的历史样本数据稀少，这使得外部市场对于发电商而言类似于黑箱，发电商难以通过建立市场博弈模型或研究对手行动制定自身报价策略。

在该情形下，强化学习［9-10］成为发电商优化自身报价策略的强大工具。强化学习的基本思想是学习者通过与未知环境的不断交互来获得最佳决策。学术界已经对强化学习在电力市场方面的应用开展了较多的研究。例如:文献［11］应用Q 学习对发电商的行为进行建模，并根据模型评估市场规则；文献［12］使用模糊强化学习来优化电力市场中发电商的报价策略。此外，近年来深度神经网络的发展进一步提升了强化学习的性能。例如，文献［13］提出了一种深度强化学习方法，并结合优先级经验回放策略来优化发电商的报价行为。文献［14］将深度强化学习算法应用于负荷聚合商的最优报价和定价策略。

然而，需要注意的是，现有研究在以下2 个方面仍存在改进空间。

1）现有研究通常笼统地将发电商报价和市场出清这一过程描述为马尔可夫博弈（或随机博弈）［15］。马尔可夫博弈是马尔可夫决策在多智能体环境下的扩展，它假定系统的当前状态与过去状态以及所有参与者的共同行动相关联。然而，马尔可夫博弈对于状态转移的严格定义，使得它依赖于特定的适用场景。在系统中可再生能源占比较高，火电机组灵活性不足的情况下，当前市场状态，例如节点边际电价（locational marginal price，LMP）会一定程度上关联上一时刻的LMP，该场景下的发电商博弈进程可通过马尔可夫博弈表示；而在系统中火电机组占比较高，且灵活性较强的情况下，当前的市场状态，仍以当前系统的LMP 为例，主要取决于负荷和发电商在当前时段的联合投标行为，而与上一时刻的LMP关系较弱，该场景下发电商的博弈进程更适合用重复博弈［16］描述。

2）虽然多数研究认可“发电商不能对整个外部环境进行完整建模”的前提，但是仍默认发电商能够获取大部分对手的历史投标信息或系统物理参数。在成熟的市场中，这种假设有一定的合理性。但是在市场启动初期，这些外部数据的获取难度将大大提高，甚至变得不可行。因此，本文假设发电商在市场初期无法获取除了自身信息（即自身历史投标、所在节点电价和利润数据）以外的任何对手和系统信息。

本文聚焦于现货市场中的实时市场，以期从发电商的角度优化其单时段报价策略。

1 重复博弈模型

1.1 发电商、用户和市场运营商模型

市场成员通常包括3 个主要部分:发电商、用户和市场运营商。古诺模型和供应函数模型是描述发电商竞价博弈的2 种经典模型。古诺模型中，发电商只报发电量；供应函数模型中，发电商报自身边际成本函数。供应函数模型更加符合市场的运作规律，在描述电力市场成员博弈中得到了广泛的应用［17］。

1）发电商

本文假设每个发电商拥有一个注册火电机组，其成本函数以二次形式表示［18］，具体如下:

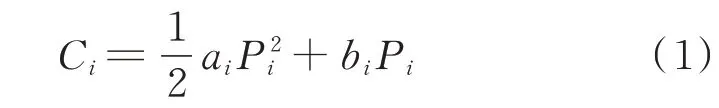
式中:i 为发电商编号；Ci为发电商i 的成本函数；bi和ai分别为发电商i 的一次项和二次项系数；Pi为发电商i 的出力。

在供应函数模型中，发电商提交给系统运营商的是自身的边际成本函数。实际上，发电商提交给市场运营商的边际成本和真实的边际成本往往存在偏差，即

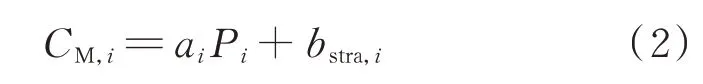
式中:CM，i为发电商i 的策略性边际报价；bstra，i为策略性因子，即可变的边际成本截距。该边际成本函数称作发电商i 的报价曲线，即为文中所指的报价。报价策略即为边际成本函数中截距的取值。

对于发电商i 而言，其目标在于最大化利润:

式中:Ji为发电商i 的利润；λi为发电商i 所在节点的节点电价。

2）用户

用户j 的效用函数也可以写成二次形式:

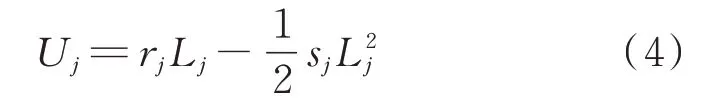
式中:j 为用户的标号；Uj为用户j 的效用函数；rj和sj分别为用户j 的一次项和二次项的系数；Lj为用户j的负荷需求。

由于本文关注发电商的报价策略，故假定用户提交真实边际效用:

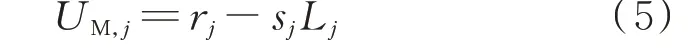
3）市场运营商

市场运营商收集发电商和用户提交的边际成本和边际效用函数，并出清市场。本文使用直流最优潮流算法实现经济调度，在联营模式下，市场运营商的目标是最大化社会福利［19］，即

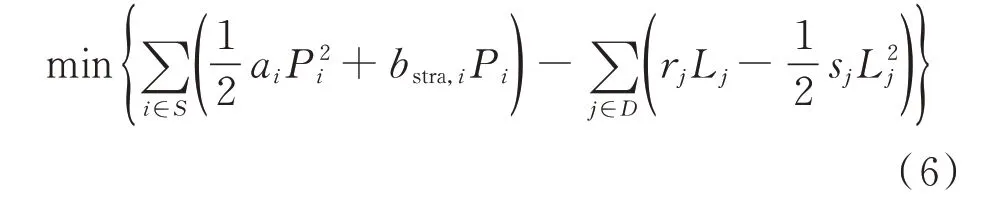
式中:S 为发电商集合；D 为用户集合。

优化问题的等式约束是发用电平衡，可表述为:

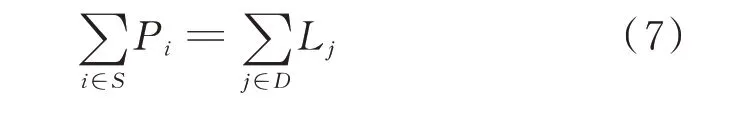
优化问题的不等式约束为线路潮流约束、发电机出力上下限约束和负荷上下限约束，可表述为:

式中:lv为传输线v 的容量；Fv为传输线v 的功率流；V 为 传 输 线 的 集 合；Pmin，i和Pmax，i分 别 为 发 电 商i 的功 率 输 出 的 下 限 和 上 限；Lmin，j和Lmax，j分 别 为 用 户j的负荷下限和上限。每条线的潮流可以根据节点负荷和潮流传输因子［20］来计算。

1.2 重复博弈

基于供应函数模型的重复博弈市场框架如图1所示，在实时市场中，发电商和用户分别将下一个小时的策略性边际成本函数和真实边际效用函数提交给市场运营商。市场出清完毕后，市场运营商计算所有发电商的发电量、用户的负荷值以及系统的节点电价［21］，并反馈给相应的市场参与者。

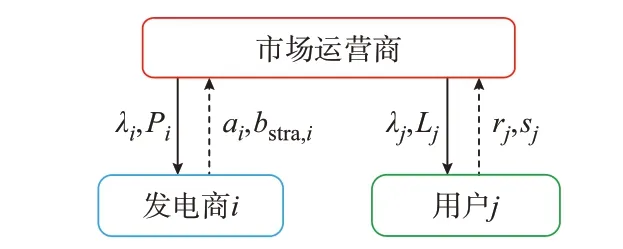
图1 基于供应函数模型的重复博弈市场框架Fig.1 Framework of repeated game market based on supply function model

在与市场的反复互动过程中，发电商可以逐渐了解市场并得到最佳的报价策略。所有发电商以该种形式参与市场竞争的博弈进程即称为重复博弈。

2 发电商策略性报价的强化学习自动机算法

连续动作强化学习自动机（continuous action reinforcement learning automata，CARLA）由 文 献［22］提出，并解释和证明了其收敛性。CARLA 算法是本文所提出的实用强化学习自动机（practical reinforcement learning automata，PRLA）的基础，本文将CARLA 的动作选取和概率密度的更新过程进行简化处理，避免复杂的符号运算和积分方程求解，在不改变算法收敛性的前提下使整个算法更加实用。

CARLA 采用非参数化概率模型。在每次迭代中，算法使用者根据动作概率密度函数随机选择动作，在与环境交互后，依照反馈信号的强弱提高或降低该动作及相邻动作的概率密度值。其本质是不断地强化更好的动作被选中的概率。经过多次与环境的交互，最终得到稳定集中在最优动作附近的概率密度函数，从而完成整个学习过程。CARLA 算法的优势在于智能体不需要过多的先验知识和复杂的超参数调整。但是该方法在实际应用中仍面临较大问题:概率密度函数的更新涉及大量的符号运算，且动作的选取涉及复杂的积分方程求解。随着迭代次数的增加，其计算时间和难度将呈指数级数上升，这使得计算代价很高甚至难以求解［23-24］。文献［22］虽然使用了插值的思想处理这一困境，但是并未深入介绍具体流程。

针对该问题，本文结合离散化和梯形法积分的思想，改进了CARLA 算法（见附录A）的选择动作和更新概率密度函数的方法，使整个算法的时间复杂度大大降低。其核心思想为:将概率密度函数离散化，以存储空间和计算精度换取计算时间的减少和计算复杂度的降低。

改进后的PRLA 算法的具体流程如下，其中步骤2 至步骤4 为循环执行阶段（当连续若干次动作的变化值小于设定阈值，循环终止）。

步骤1:初始化动作空间概率密度函数及历史收益缓存区。

对于某个发电商而言，其报价策略取值的动作范围x∈［xmin，xmax］（xmin即为b 取值下限bmin，xmax即为b 取值上限bmax）。发电商对不同策略的选择偏好通过在动作空间上概率密度函数的形式表示，记作f（x，n），其中n 表示发电商与市场之间的迭代次数。由于在初始阶段，发电商没有关于市场的先验知识，其不同行为的选择偏好相同，一般采用在动作空间上的均匀分布表示初始概率密度:

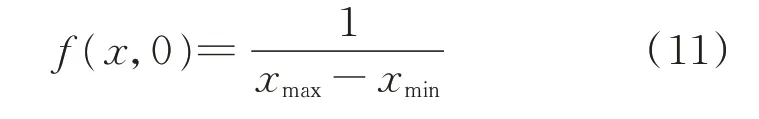
同时，发电商初始化历史收益缓存区，用于存放每轮迭代的收益，缓存区初始存放数据为0。

步骤2:选择动作。

在第n 次市场出清，发电商根据最新的概率密度函数选择动作。首先，生成符合在［0，1］区间上均匀分布的随机数z（n），并根据z（n）和概率密度函数选择动作x（n）。

具体做法是，PRLA 算法将动作区间m 等分，记为{ x0，x1，…，xm}，每段长度为xd，称为1 个子区间。这里用概率密度函数在m+1 个区间端点的离散值代替原连续概率密度函数参与运算，即在第n 次迭代 ，离 散 概 率 密 度 函 数 值 为 { f (x0，n)，f (x1，n)，…，f (xm，n)}。

根据梯形法［25］，计算任意子区间k 的面积:

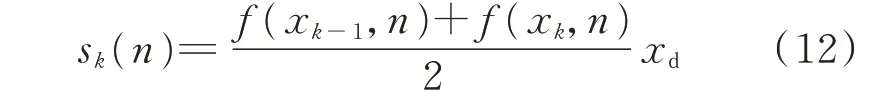
计算动作累积概率S，即子区间面积的递加:

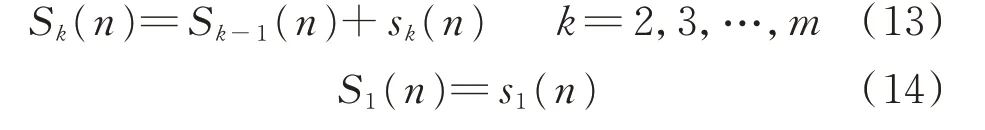
在选择动作时，首先根据累积概率确定z（n）所在子区间u，则x（n）可表示为:

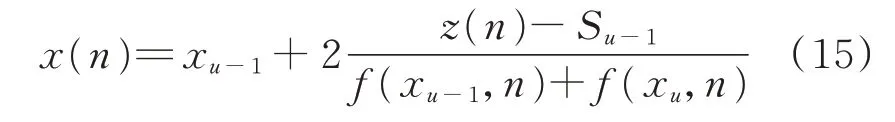
附录B 举例说明该动作选取过程。在选择边际成本的截距之后，发电商将报价提交给市场运营商。

步骤3:对环境反馈做出评估。

在所有发电商和用户分别提交自身边际成本和边际效用函数后，市场运营商执行市场出清程序。市场出清完毕后，发电商根据式（3）得到出清收益J（n），并执行强化信号评估:

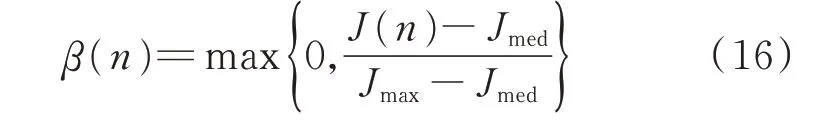
式中:Jmax和Jmed分别为历史收益缓存区中的最大值和中位数。

该步骤的作用是评估强化信号的强弱:β（n）越大，奖励信号越强；反之，则惩罚信号越强。在执行完评估后，将J（n）存入缓存区。为了避免过多消耗存储空间，同时使学习过程跟上环境的不断变化，算法设定只能将最新的L 个数据保存到数据缓存区中。

步骤4:更新概率密度函数。

首先，引入对称高斯邻域函数h（n）（见式（17））作为更新信号，其目的是在每次迭代中，强化表现好的动作及其周围动作被选择的概率。

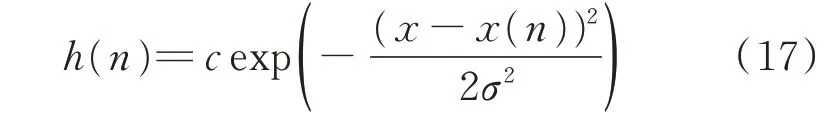
式中:c 和σ 分别为高斯分布的高度和宽度，其值可以决定学习速度和分辨率。通常c 越大，学习速度越快，但是学习结果往往越不准确。σ 越大，概率密度变化越平缓，但是学习结果分辨率越低。

同样地，将更新过程离散化。在第n 次迭代，离散概率密度函数的更新可以表示为原离散概率密度函数和离散高斯邻域函数在子区间端点处离散值{h(x0，n)，h(x1，n)，…，h(xm，n)}的线性运算，即

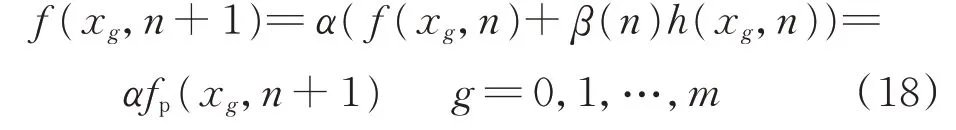
式中:α 为归一化因子，可使概率密度函数的积分保持为1。α 值可由式（19）所示复化梯形公式确定。

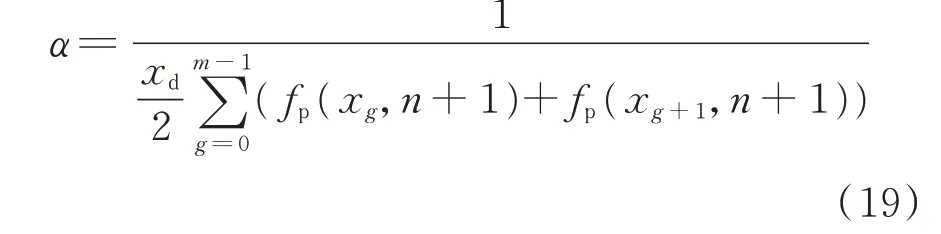
附录C 举例说明了该概率密度函数更新过程。在迭代过程中，概率密度函数始终以离散的形式储存和运算。上述离散化处理由于未改变其整个算法的迭代逻辑，故并不影响算法的收敛性。算法的伪代码见附录D。

3 算例分析

仿真软件为MATLAB 2020a，运行环境为搭载Intel Core i7TM的16 GB RAM 的服务器。算例的主要目标在于验证所提出PRLA 算法在平稳和非平稳环境［26］下的有效性，并通过重复试验评估算法的稳定性。

测试系统的拓扑结构如图2 所示。每个节点都有一个发电商和一个用户。表1 列出了所有参与者的参数。

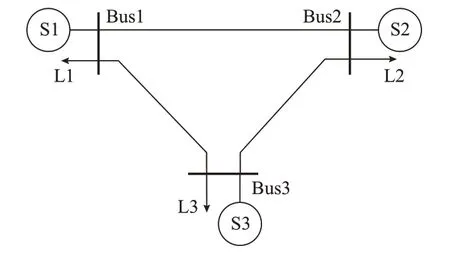
图2 3 节点测试系统拓扑Fig.2 Topology of 3-bus test system

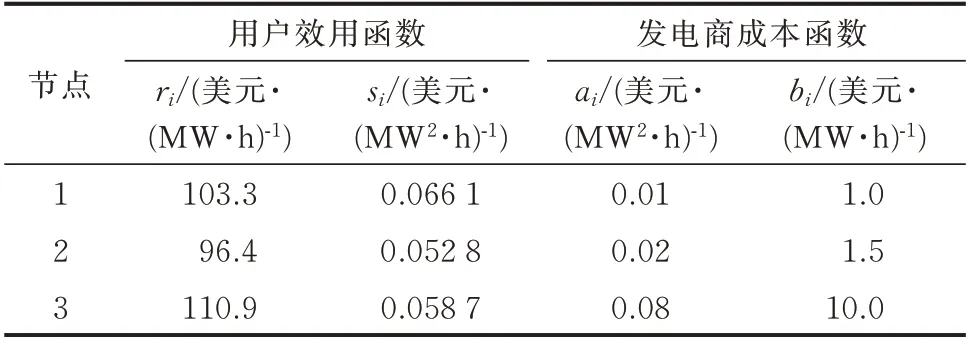
表1 测试系统中的发电商和用户参数Table 1 Parameters of power suppliers and consumers in test system

发电商3 的成本参数设置较大，这是为了突出不同发电商的市场力。此外，本文采用直流潮流模型，每条传输线的电抗设为0.1 p.u.。为了更好地反映PRLA 算法的有效性，将Bus1-Bus3 线路的传输极限设置为100 MW，以造成系统阻塞。表2 显示了在完全信息下的迭代方法［27］计算的报价策略纳什均衡点，这是理想情况下发电商的最优报价策略。

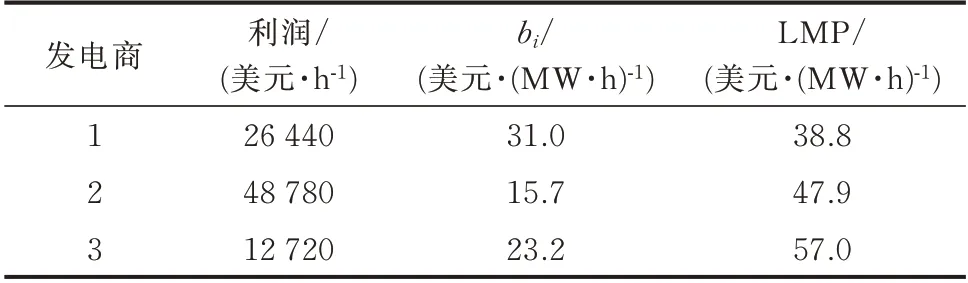
表2 解析纳什均衡点Table 2 Analytical Nash equilibrium point

本文将通过PRLA 算法求得的数值解（记为SL）与表2 中的解析解（记为SA）进行对比，并计算百分比误差（DPE）作为衡量指标:

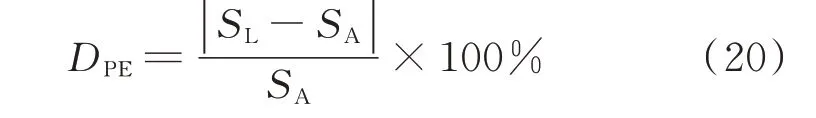
3 个发电商从开始博弈到报价策略收敛到纳什均衡为一轮完整的学习过程。为了更好地反映算法的性能，本文取100 轮完整学习过程的平均数据计算百分比误差，以平抑单轮学习过程中的不确定性，增强了结果的可信度。

本文假设机组的灵活性充足，并根据此假设给出报价上下限bmax和bmin分别为50 美元/（MW·h）和0 美元/（MW·h），同时，设区间数M 为500 个，c 和σ分 别 为0.1 美 元/（MW·h）和0.5 美 元/（MW·h）（c 和σ 的 灵敏度分析见附录E），收敛判据ε 设定为1 美元/（MW·h），数据缓存区的长度L 设置为10。需要指出的是，本文虽设定了收敛判据，但是每轮迭代中，发电商在策略收敛后仍迭代至400 次，以保证不同收敛曲线的起始点与终止点对应。

3.1 平稳环境

本算例中，平稳环境是指假定发电商2 和发电商3 具有全局视角，直接以其各自的纳什均衡最优解固定边际成本，而发电商1 则需要使用PRLA 学习其最优报价策略。在这种情况下，若发电商1 能够同样收敛到其纳什均衡解，则证明算法的有效性。

发电商2 和发电商3 分别固定截距为15.7 美元/（MW·h）和23.2 美元/（MW·h）。发电商1 通过学习将报价策略优化为31.0 美元/（MW·h），与解析解31.0 美元/（MW·h）一致，证明了平稳环境下算法的有效性。

平稳环境下，发电商1 的学习过程经过约130 次迭代后逐渐稳定，其报价策略概率密度函数的峰值逐渐稳定在纳什均衡解（31.0 美元/（MW·h））附近。发电商1 的报价策略曲线如图3（a）所示，报价策略概率分布变化过程如图3（b）所示。

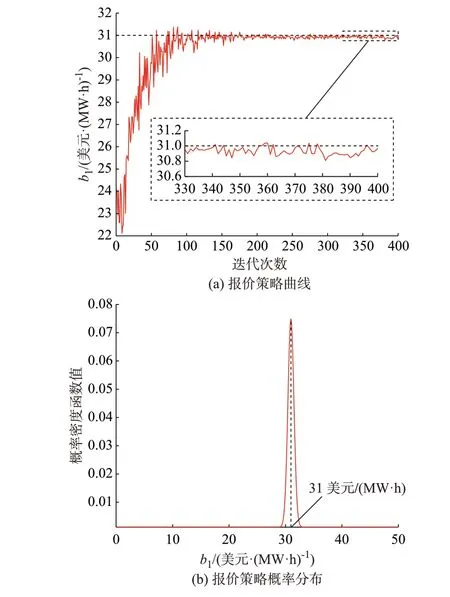
图3 平稳环境下发电商1 的报价学习过程Fig.3 Bidding learning process of power supplier 1 in steady environment

3.2 非平稳环境

本算例中，非平稳环境是指所有发电商均需要通过学习以获得自身策略。简便起见，假定所有发电商均采用PRLA 算法。在这种情况下，若所有发电商仍能够收敛到纳什均衡解，即可证明算法的有效性。3 个发电商所使用的PRLA 算法的参数与上文相同。

表3 列出了这3 个发电商的学习结果。

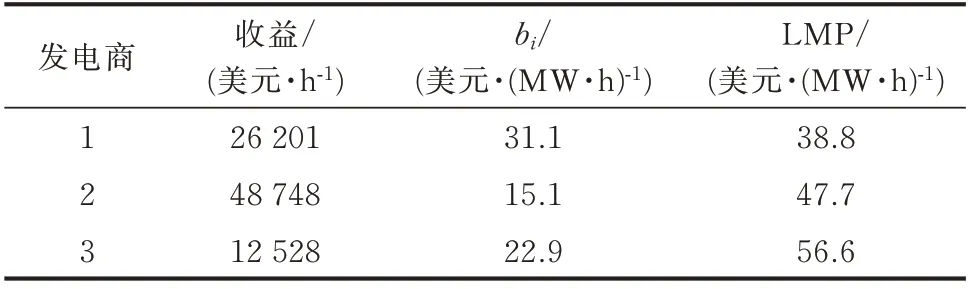
表3 非平稳环境学习结果Table 3 Learning result in the non-steady environment

3 个发电商学习到的最佳报价策略分别约为31.1、15.1、22.9 美 元/（MW·h），其 百 分 误 差 均 在4%以内，证明了非平稳环境下的算法有效性。

非平稳环境下，发电商1 的学习过程经过约245 次迭代后逐渐稳定。随着迭代次数的增加，发电商1 报价策略概率分布的峰值逐渐稳定 在31.1 美 元/（MW·h），与 纳 什 均 衡 解 析 解（31.0 美元/（MW·h））的误差为0.32%。发电商1的报价策略曲线如图4（a）所示，报价策略概率分布变化过程如图4（b）所示。

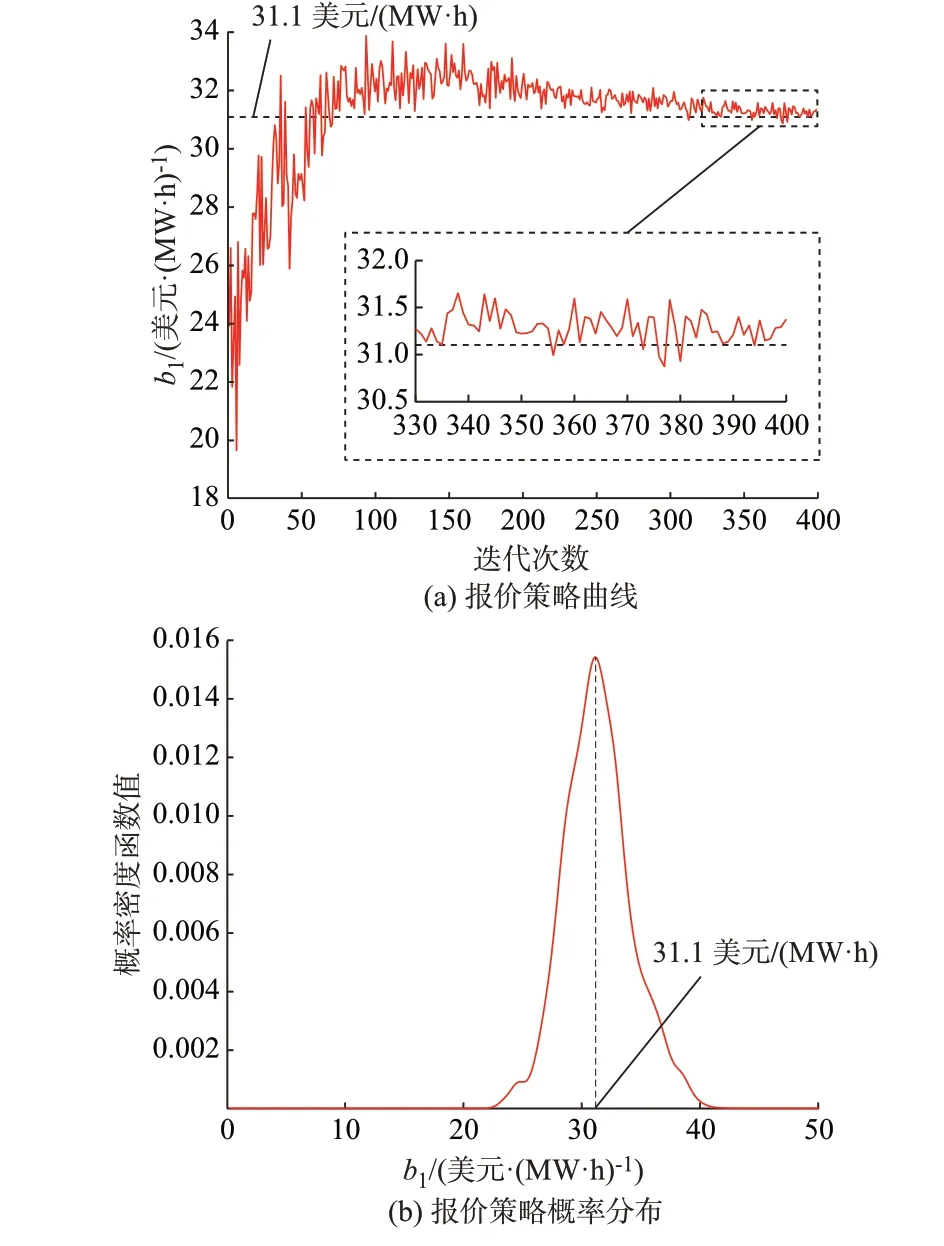
图4 非平稳环境下发电商1 的报价学习过程Fig.4 Bidding learning process of power supplier 1 in non-steady environment

4 结语

本文着力于解决有限信息环境下发电商的策略性报价问题。首先，将发电商的博弈过程建模为重复博弈。进一步，提出了一种PRLA 算法，以帮助发电商在信息不完全的情况下优化报价策略。该算法在平稳环境和非平稳环境下学习结果的百分比误差均在4%以内，其有效性得到验证。该方法适用于在电力现货市场启动初期指导发电商的策略性报价行为，在中国电力市场改革的背景下具有一定的借鉴意义。

本文的报价方法的基础是供应函数模型，但也可以拓展到其他模型下，如分段报价模型。未来的工作将集中在以下几个方面:对环境不确定性的更加准确的建模；算法实际使用过程中效率的提高；考虑发电商多时段报价的优化问题，并涉及机组组合。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。