小波分析法在海拉尔地震台前兆数据处理中的应用研究

曲浩鑫，王 怡，堵伟鹏

(内蒙古自治区地震局海拉尔地震台，内蒙古 海拉尔 021000)

0 引言

小波分析是一种包含尺度伸缩和时间平移的双参数函数分析方法，能将一个信号分解成对空间和尺度的独立结果, 同时又保留原信号所包含的信息[1]。基于小波变换能分离出不同频带的信号，目前，小波分析法广泛应用于天然地震震相识别，重力、大面积形变测量和定点形变测量等地震异常分析中[2-7]。宋治平等研究表明，小波分析法对形变数字化资料中的干扰识别与消除、不同频率潮汐波的分离、趋势异常与短期异常的提取等方面都具有较强的功能[8]；张军等应用小波分析法对地下流体资料进行研究，得出较好抑制流体数据中随机噪声的方法，并通过重构小波系数达到消除降雨干扰的目的[9]；刘建明等研究得出小波分析可作为提取定点形变异常的一种有效方法，通过将定点形变观测数据分解成不同频段，对提取异常信号有较好的效果，提高了识别地震信息的能力[6]；倪友忠等通过小波变换法对面应变日均值进行分析，发现在海域大震前，小波变换第三阶细节部分在震前出现持续数月以上的高频脉冲，且面应变有鼓包现象[10]。

因此，在小波变换理论基础上，运用小波分析法对海拉尔地震台(以下简称海拉尔台)前兆数据进行处理，总结小波分析在前兆资料中的应用经验，以期为识别、提取及去除前兆异常信息提供新思路。

1 小波分析理论基础

此时称Ψ(t)为一个基本母小波，将母函数Ψ(t)经伸缩和平移后得到如下公式：

式中：a为伸缩因子；b为平移因子。称其为一个小波序列。在实际运用中，连续小波必须加以离散化。任意函数f(t)的离散小波变换可表示为：

为区分不同分量信息，引入构造正交小波的方法和小波变换的快速算法—Mallat。应用Mallat算法不必知道具体的小波函数，同时，也使小波变换在计算上变得可行。Mallat一维分解算法可表示为：

式中：Cj+1f与Dj+1f是在分辨率为j时的近似部分和细节部分。对于Mallat一维重构算法可表示为：

Cj-1[n]=∑nh(n-2k)Cj[k]+∑ng(n-2k)Dj[k],

式中：Cj[k]为低频系数；Dj[k]为高频系数；h，g分别为低通和高通滤波器。

2 小波基函数的理论选取

在Mallat算法中小波基函数的选择不是唯一的，所有满足小波条件的函数都可作为小波函数，不同的小波基函数使信号的分解和重构有不同的结果。因此,选取合适的小波基函数就显得较重要。目前，常用的小波基函数有：Haar小波、Daubechies(dbN)小波系、Biorthogonal(biorNr.Nd)小波系、Coiflet(coifN)小波系、SymletsA(symN)小波系、Morlet(morl)小波、Meyer小波等。常用小波基函数的主要特点如表1所示，选取的小波基函数既能突出异常信号又能最大限度地保留前兆资料的固体潮信息。

表1 常用小波基的主要特点Table 1 Main characteristics of commonly used wavelet bases

根据小波函数的定义和常用小波基的特点，结合前兆信号资料的特征及研究目的，综合考虑小波基函数的对称性、正则性、紧支撑性及消失矩的阶数[6,12-16]。理论上，Daubechies(dbN)小波系中的db4小波基函数能满足前兆资料处理的要求。db4小波的尺度函数和小波函数如图1所示，较好地兼顾了紧支撑性和正则性，同时，消失矩的阶数也较合适，能在保留固体潮信息的基础上较好地反应异常信号。

为检验db4小波在实际前兆数字化资料处理中的效果，选取2020年1月24日海拉尔台垂直摆NS分量数据进行小波变换，图2为应用db4小波基函数进行离散小波变换的结果。可以看出，2020年1月24日15点09分塔吉克斯坦5.6级地震的信号在高频分

图1 db4小波尺度函数及小波函数Fig.1 db4 wavelet scaling function and wavelet function

解中变得突出，同时，应用近似5阶小波重构消除了该地震波对垂直摆正常波形的影响，垂直摆的固体潮信息被较好地保留。由此可见，应用db4小波基函数进行离散小波变换对海拉尔台前兆异常信号的识别、提取及消除是适用的。

图2 垂直摆NS分量曲线Fig.2 NS component curve of vertical pendulum

3 小波分析剔除干扰

海拉尔台目前共有5套数字化前兆观测仪器，前兆资料信息量大且不同仪器会受到不同程度干扰，在原始曲线中不易识别和区分。小波变换理论具有较强的干扰识别和排查能力，因此，选取海拉尔台受气压干扰和场地环境影响的典型事件，采用小波分析法进行识别和消除干扰。

3.1 气象干扰

第22页图3a为2020年8月2日至12日伸缩仪NS分量原始数据曲线，第22页图4a为2020年7月1日至3日水管仪NS分量原始数据曲线，从图中难以识别出具体的干扰时段。应用小波变换法对图3a、图4a原始数据曲线进行细节8阶分解，分解细节部分如图3d、图4d所示。可以看出，d1-d2未见明显异常，从d3开始曲线出现明显异常(图中方框部分)，上下波动幅度超过2倍中误差。通过与同时段气压变化曲线进行对比发现，d3-d6明显的上下阶跃部分与气压异常波动时段一一对应，因此，可以判定伸缩仪和水管仪的异常变化由气压突变引起。

在小波分解d1-d8中，d1-d4主要是高频信号段部分，d5-d8为低频信号段部分，气压影响在d3-d6部分清晰显示，d8频带部分明显过滤了异常变化，显示的是固体潮信息。综上所述，海拉尔台形变仪受气压干扰在小波分解d3-d6部分较明显。

图3c为通过小波重构剔除受气压影响后的曲线，与原始曲线图3a相比，在保留原始信息的情况下，较好地去除了气压影响造成的固体潮畸变，证明小波分析法对排除气压干扰具有较好效果。

图3 伸缩仪2020年8月2日至12日NS分量曲线Fig.3 NS component curve of extensometer from August 2 to 12, 2020

图4 水管仪2020年7月1日至3日NS分量曲线Fig.4 NS component curve of water tube instrument from July 1 to 3, 2020

3.2 场地环境干扰

由第23页图5a看出,从2018年10月25日10时30分左右至27日8时30分左右，伸缩仪受干扰出现固体潮畸变，经核查为体应变钻新井工程影响所致，属于典型的场地环境干扰。通过小波细节8阶分解显示有3个异常时间段(见图5c)，分别为25日10时至16时、26日 13时至22时、27日7时至8时，三个时间段与三次钻井时间相吻合。从图5a原始曲线中较难判断出具体受干扰的时段，小波分解d3-d6部分压制了其余信息，将场地环境干扰凸显出来，其中细节5阶最为明显。将场地环境干扰信息提取之后对原始曲线进行干扰剔除，剔除结果如图5b所示。与原始曲线相比，曲线光滑度高，高频干扰信号基本被抑制。

图5 伸缩仪2018年10月25日至27日NS分量曲线Fig.5 NS component curve of extensometer from October 25 to 27, 2018

4 小波分析地震与爆破

4.1 小波分析近震与远震

海拉尔台不同前兆仪器识别地震的能力不同，多种手段互补观测可以清晰地记录到远震、近震以及地方震的同震效应[8，10]。对于前兆分析来讲，这种同震效应幅度大，夹杂在观测曲线中，过大的振动幅度会压制前兆仪器正常的固体潮信息，也属于一种干扰。因此，采用小波分析法对同震效应造成的突跳进行识别和处理是必要的。

图6a为海拉尔台2017年5月12日重力潮汐观测值原始曲线，可以看出，呼伦贝尔市鄂伦春旗3.7级地震明显，中美洲沿岸远海6.2级地震难以辨别。从图6c中看出，d1-d8中有两处明显异常，是由19时11分的中美洲沿岸远海6.2级远震和22时19分的呼伦贝尔市鄂伦春旗3.7级近震造成的，在原始曲线上难以辨别的中美洲沿岸远海地震经过小波变换后清晰可见。第24页图7a为海拉尔台2019年9月30日垂直摆EW分量原始曲线，其中，智利中部沿岸近海地震为远震，呼伦贝尔市新巴尔虎右旗地震为近震，近震在原始曲线中不明显，经过小波变换后可轻易识别。

由图6c、图7c看出,近震和远震在小波变换细节分解中具有完全不同的特征，远震在d3-d5阶中异常明显；近震在d1-d3、d6-d8阶中较明显，d1-d3阶异常幅度逐渐减弱，d6-d8阶异常范围的宽度逐渐增加。图6b、图7b为去除干扰后的重力潮汐观测曲线，比原始数据曲线清晰，日变形态正常显现。通过以上分析可以得出，小波分析对同震效应的识别、提取及干扰消除均具有较好的效果。

4.2 小波分析爆破

第24页图8a为海拉尔台垂直摆NS分量2019年6月10日原始数据曲线，可以看出，11时左右北南分量数据形态表现为上下阶跃，难以判断此阶跃是由地震还是爆破引起。因此，对曲线进行小波细节8阶分解，结果如图8b所示。对比图8b、8c发现，爆破与地震两种信号在小波细节分解上有明显区别。爆破信号在小波分解d1-d8阶中均清晰可见，异常的宽度和幅度变化不大；地震信号在d1-d8阶中的某几部分异常明显，同时，地震类型的不同，异常的宽度和幅度变化呈现不同的态势。这是由于地震信号比爆破信号复杂，信号的频带范围更宽所致。第25页图9为海拉尔台2020年4月7日垂直摆EW分量记录到的爆破，通过做小波分解发现与图8具有相同的规律，即在小波分解d1-d8阶中爆破信号的宽度和幅度变化不大。由此可见，利用小波细节分解辨别原始信号异常是由地震还是爆破引起具有较好的效果。

图6 2017年5月12日重力仪曲线Fig.6 Gravimeter curve of May 12, 2017

图7 2019年9月30日垂直摆曲线Fig.7 Vertical pendulum curve on September 30, 2019

5 结论与讨论

通过以上分析，得出如下认识：

(1) 小波变换可将不同频带的信号较好地分离，实现对各频段小波系数的逐一分析，从而达到提取前兆异常、去除特定频段干扰的目的。

(2) 通过对不同小波基函数特征的归纳分析,并对前兆资料进行处理，验证了db4小波是海拉尔台前兆数字化资料处理较适合的小波基函数，能满足在保留固体潮信息的基础上检测前兆异常。

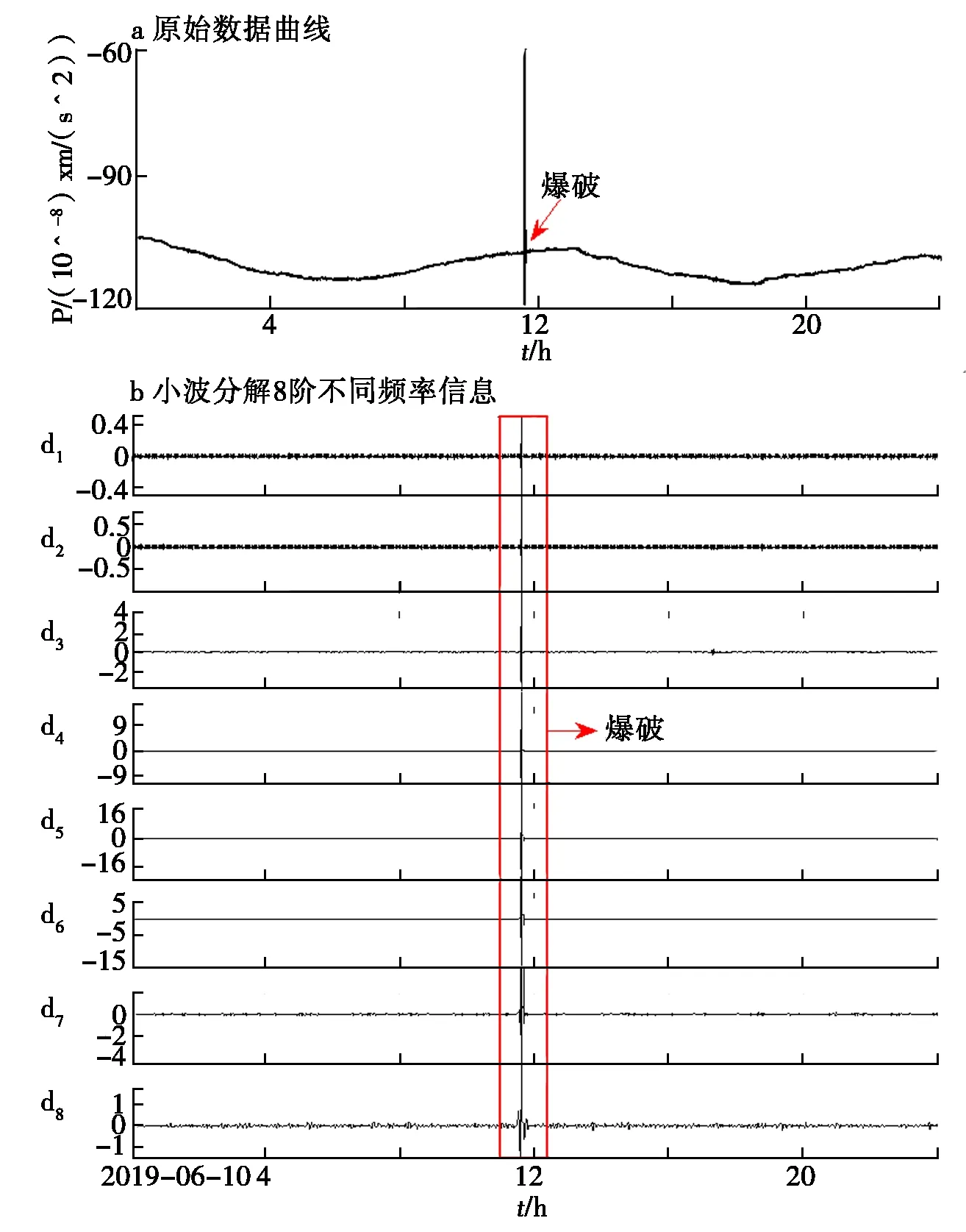
图8 垂直摆2019年6月10日NS分量曲线Fig.8 NS component curve of vertical pendulum on June 10, 2019

图9 2020年4月7日垂直摆EW分量曲线Fig.9 EW component curve of vertical pendulum on April 7, 2020

(3) 由海拉尔台形变仪器小波分析结果可知，小波分析法对气压、场地环境干扰的识别和剔除具有较好效果。气压、场地环境干扰均在小波细节分解d3～d6部分异常显著，其中d5阶最明显，d8阶表征的基本是固体潮信息。应用小波变换重构信号基本去掉了气压、场地环境对原始信号的影响，去噪效果显著，信号曲线光滑度高，基本抑制了噪声信号。

(4) 小波变换法在海拉尔台同震效应的识别、提取和去除具有较好效果。通过对比远震和近震小波变换结果得出，远震在小波细节分解d3-d5部分异常显著，近震在小波细节分解d1-d3、d6-d8部分明显，且d1-d3部分异常幅度逐渐减弱，d6-d8部分异常范围的宽度逐渐增加。

(5) 利用小波细节分解法可对原始异常相似的地震和爆破信号进行辨别。地震信号只在小波细节分解d1-d8阶中的某几部分异常明显，同时，地震类型的不同，异常的宽度和幅度变化呈现不同的态势；爆破信号在小波细节分解d1-d8阶中均清晰可见，异常的宽度和幅度变化不大。