堆石混凝土坝渗透系数浅析

龙召福，唐晓玲

(贵州大学土木工程学院，贵州 贵阳 550025)

堆石混凝土(Rock Filled Concrete，RFC)是利用具有高流动抗离析性能的自密实混凝土(Self-Compacting Concrete，SCC)，依靠自重填充到预放堆石体空隙中而形成的新型混凝土[1]。堆石混凝土具有施工速度快、施工成本低、综合性能较高、节能环保[2]、水化热温升低[3]等优点，因此正在被广泛应用于具有大体积混凝土的坝体建设中[4- 8]。用堆石混凝土浇筑而成的大坝，其抗渗性能是一项关键的检测指标，直接影响到大坝的耐久性，抗渗性能太差甚至还会引发坝体的大量渗漏。而渗透系数是评定坝体透水性能的指标之一，也是进行渗流计算过程中的一个重要参数，对此研究具有重要意义。

由于堆石混凝土具有独特的成型方式，以及坝体块石粒径一般大于30cm，使其各项性能区别于普通的混凝土。已有学者对其进行了多种性能的试验，金峰、安雪晖等[9]用钢模制做了边长分别为600mm和500mm的立方体堆石混凝土，以及相应尺寸和标准尺寸的自密实混凝土，通过抗压试验，得到对应的强度值。李友彬、朱柏松等[10]在现场同条件浇筑了边长为2.2m的试验仓，通过绳据切割成边长为450mm的立方体及边长为450mm、高为900mm的长方体试块并对其进行了抗压、劈裂抗拉和静力弹性模量等试验。而在堆石混凝土抗渗的研究中，刘昊[11]把堆石混凝土简化为单元混凝土，对其进行了抗渗等级试验，用粒径大小为10～15cm，直径450mm、高450mm的混凝土试件进行全级配渗透试验，以及对其进行室内的压水试验，得到了渗透系数。秦根泉、梁必块[12]实地浇筑2m的立方体试块，通过钻孔得到芯样并进行渗透试验而得到渗透系数。文献[13- 14]在室内浇筑大试件，通过切割、打磨和填补形成标准截头圆锥试件，然后进行渗透试验。

以上学者通过制做大于常规尺寸的堆石混凝土试件，在力学性能试验中较真实地反映了试验结果。而对于渗透试验，目前所用的试件尺寸都较小，虽然全级配渗透试验所用的尺寸较大，但目前试验次数少。本文通过对堆石混凝土坝体钻孔压水所得到的数据进行理论换算为渗透系数，再对室内、现场渗透试验、理论公式和计算结果进行分析比较，进一步揭示了堆石混凝土的渗透性能。

1 理论分析

根据SL 352—2006《水工混凝土试验规程》[15]的要求，在室内进行混凝土渗透渗透系数测定时有两种方式：全级配混凝土渗透系数试验和混凝土相对渗透试验。由于我国工程上习惯用抗渗标号来表示大坝混凝土的抗渗性，一般后者应用得较多。

对于全级配混凝土渗透系数公式，其公式是根据达西定律变形而得到：

(1)

式中，K—岩体渗透系数，cm/s；Q—压入流量，cm3/s；H—试验水头，cm；L—试段长度，cm；r0—钻孔半径，cm。

在由钻孔压水推求来的渗透系数公式中，根据水的流动形态，通常有两种假设模型[18]。一种为辐射流型，该模型假定水流垂直钻孔轴线对称流动，并限制在压水孔段内，如图1所示。

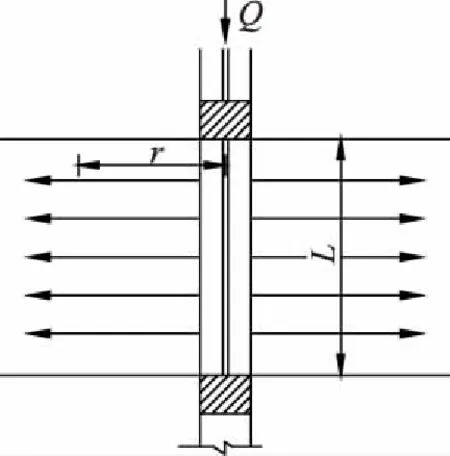
图1 辐射流型简图

文献[19- 20]中假定岩层内的透水性为各向同性，当压入钻孔内的流量和压力相对稳定时，对于任意以钻孔轴心为半径的圆柱断面的流量相等[19- 20]。由达西定律：

Q=KJA

(4)

距离钻孔轴心任意微段出的水力坡度及该处的断面面积为：

(5)

在钻孔半径r0和距钻孔轴心R段内，由式(4)—(5)对其积分：

(6)

式中，r0—钻孔半径，cm；R—影响半径，cm；H0—钻水孔内的总水头，cm；HR—距钻孔轴心R处的总水头，cm；其余同上。

另一种为椭圆体流型，该模型假设水流以钻孔轴心为线源均匀向四周流出，如图2所示。

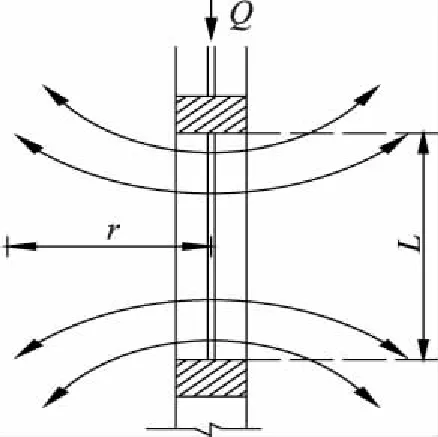
图2 椭圆体流型简图

其渗透系数计算公式为：

(7)

由钻孔压水试验转换到渗透系数的公式比较多，文献[21]中的巴布什金经验公式：

(8)

式中，a—与试段位置有关的系数，当试段底至隔水层的距离大于L时为0.66，反之为1.32。

文献[22]中，在吕荣值Lu小于20时，公式如下：

(9)

近似的计算：

1Lu=(1～1.3)×10-5cm/s

(10)

或者用C·库兹纳尔推荐的曲线查吕荣值Lu与渗透系数K之间的关系。

2 试验计算方法的分析

2.1 室内试验方法分析

在SL 352—2006中混凝土渗透系数的测定方法有两种，即在1.1节对应的相对渗透系数试验测定和全级配渗透系数试验测定。对于第一种试验，文献[11]中在试模中预先放置一块粒径约为10cm的块石，然后浇筑自密实混凝土，不对其振捣，用单元堆石混凝土来模拟堆石混凝土。但是从作者试验中得到的堆石率(见表1)看，其远远低于实际工程通常55%～60%的堆石率[9]。文献[13]中浇筑了2m×1m×1.8m的堆石混凝土试块，并切割成尺寸为12cm×12cm×15cm的试件，在四周打磨后，用自密实砂浆进行填补成试验的标准尺寸进行渗透测定，但试验结果表明：与砂浆结合处渗漏较多。而文献[14]中通过浇筑好的试块切割成20cm×20cm×15cm的试件，然后直接打磨成标准尺寸的圆台体进渗透试验。但两者由于标准试模尺寸的限制，切割后的尺寸不具有代表性。

表1 单元堆石混凝土堆石率

对于第二种试验，文献[11]中在试模中预先放置粒径约为10～20cm的块石，然后浇筑成形进行试验[11]。其试件的堆石率(见表2)接近实际工程通常的堆石率，粒径虽然不能达到工程上通常的30cm，但相对于第一种试验，其更具有代表性。

由以上的分析可以得出：采用全集配混凝土的渗透试验方法较相对混凝土渗透系数试验方法更加合理。

表2 全集配堆石混凝土堆石率

2.2 现场计算方法分析

对于大坝的渗透检查，国内外通常采用钻孔压水的方法，并据此来计算坝体混凝土的渗透系数[23]。由钻孔压水推导出的渗透系数公式很多，文献[24]和SL 31—2003《水利水电工程钻孔压水试验规程》中的条文说明均指出其计算结果大致相差±20%之内。在1.2节中由假定辐射流型推导出的公式(6)可知，当影响半径R等于钻孔试段长度L，并且此时影响半径处的水头HR=0时，式(6)即转化为式(3)。对处于非饱和状态的大坝混凝土来说，钻孔压水后，水流总体形式为一饱和圈逐渐扩大的非恒定渗流过程，但压水稳定后，饱和圈中的水流可以看成为饱和稳定渗流并且饱和圈外的压力水头为0[25]；尽管在一般的压水历时内，稳定渗流难以达到，但是通过文献[26]对岩体稳定和非稳定渗流的计算可知两者相差不大，见表3。

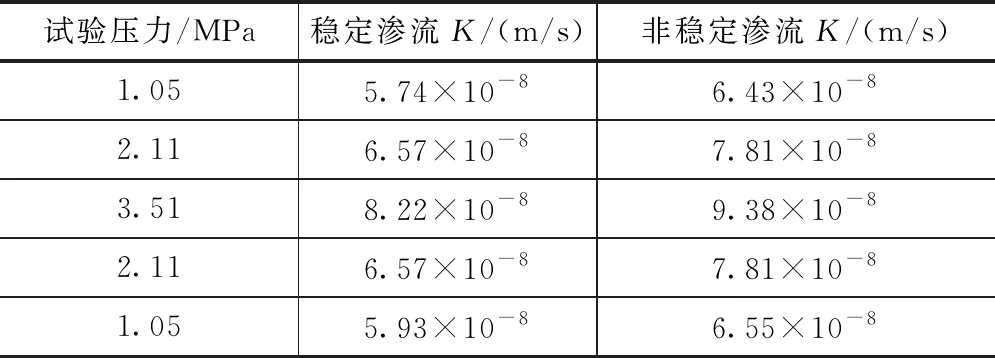
表3 渗透系数计算对比

此外，文献[18]对于非饱和区中：HR=0、R的值很小，一般可用钻孔试段长度L取代；由此可以看出，这样的简化假设是合理的。但是对于混凝土中的钻孔压水，渗流的形态并不是水平的，辐射流型这种假设模型并不理想，而椭圆体流型这种模型较为合理。从1.2节中的式(7)可以看出：当试段长度L远远大于钻孔半径r0时，其式(7)可以转换为式(6)，那么以椭圆体流型这种假设来考虑就是我们希望看到的。一般对于试段长度是远大于钻孔半径的，但一直以来人们都未能见到该公式的具体的推导过程，缺乏考证[27]，笔者也未能找到，所以理论上较为清楚的是辐射流型这种模型。

对坝体渗透系数，也可以通过1.2节中的式(8)—(10)计算或查C·库兹纳尔曲线图。对于式(9)中的吕荣值Lu，由于钻孔直径的不同而存在一定的误差，但影响微小可以忽略不计[17]。而式(3)可以通过一定的转换，变成式(9)，两者是等同的，式(9)中渗透系数的单位为cm/s。

由以上的分析可以得出：现场渗透系数的计算方法较多，且都存在近似性，理论较为完备的是辐射流型模型，对于堆石混凝土的渗透系数公式可采用简化后的式(3)。

3 实际数据计算

3.1 室内试验的渗透系数

在室内对堆石混凝土进行的渗透试验，目前笔者收集到的资料中主要有4种形式：①全集配混凝土渗透试验；②相对混凝土渗透试验；③现场取芯(芯样直径150mm)然后拿到室内试验；④室内钻孔压水(试件为直径450mm、高450mm的圆柱体)。

对第1种采用式(1)计算渗透系数，见表4。

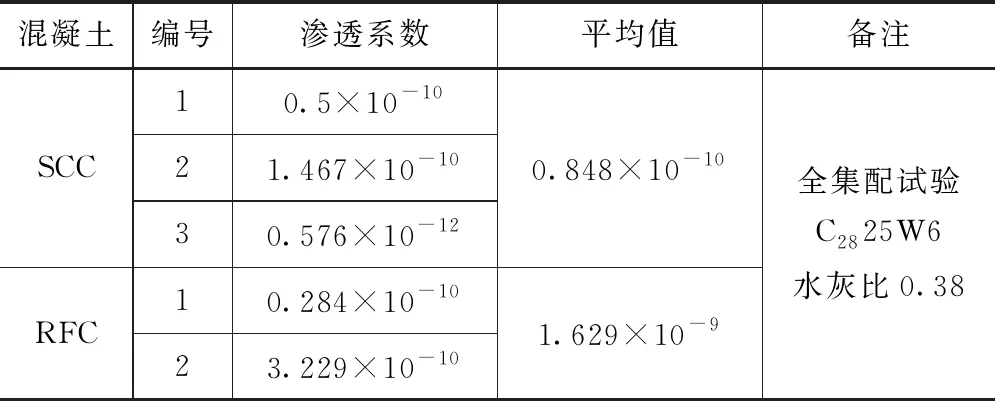
表4 全集配混凝土渗透数据 单位：cm/s

第2种试验相关学者只是进行了抗渗等级测定而得出抗渗标号，笔者采用文献[16]中抗渗标号换算为渗透系数的近似公式进行换算，见表5。

第3种试验由于收集到的资料中没提及采用什么形式的试验，只能得到用芯样测得的渗透系数值。在文献[12]中，采用实地浇筑2m的立方体试块(SCC设计等级为C2815W4、水灰比为0.3)，进行钻孔取芯后得到的渗透系数为4.01×10-8cm/s。

第4种试验文献[11]首次尝试在室内用直径450mm、高450mm的圆柱体试验进行室内压水试验，其采用式(3)计算，见表6。

3.2 现场试验的渗透系数

在贵州打鼓台水库，对坝体进行钻孔压水试验得到的数据，经过式(9)或式(3)计算得到渗透系数，见表7。同理对贵州另外4座堆石混凝土坝的渗透系数进行计算，把5座水库计算的结果分别以平均渗透系数方式表示，结果见表8。

为使在堆石混凝土坝体得的渗透系数更具有延伸性，通过文献[28]在云南地区某水库(自密实混凝土设计标号C15W6、水灰比0.39)钻孔压水所得数据，笔者再利用式(3)计算，得到该坝的平均渗透系数为2.915×10-5cm/s。

4 试验结果分析

4.1 总体结果分析

在室内试验中：①从全级配混凝土渗透试验结果(见表4)可以得到：SCC和RFC混凝土渗透系数的平均值为分别为0.848×10-10、1.629×10-9cm/s，两者相差约1个数量级，在排除其它因素影响的前提下，说明块石对该试件的渗透系数有影响；②从相对混凝土渗透试验结果(见表5)可以看出：序号1中，换算得到的SCC渗透系数值小于1.97×10-10cm/s，RFC为0.558×10-9cm/s，两者与①中结果变化不大，也可说明SCC抗渗作用被块石削弱。序号2中，RFC中的普通部位和热缝渗透系数的平均值为1.990×10-10cm/s，较序号1和①中的RFC提升了一个数量级；③由现场芯样得到的RFC渗透系数为4.01×10-8cm/s，比①、②分别相差了1、2个数量级；④通过室内钻孔压水得到的SCC和RFC渗透系数平均值分别为1.131×10-9、2.008×10-9cm/s。

表5 相对混凝土渗透数据

表6 室内压水数据

表7 坝体渗透系数

表8 坝体平均渗透系数 单位：cm/s

由以上可知室内的多种试验中，SCC渗透系数：0.848×10-10～1.131×10-9cm/s，变化不大，由①、④得到其总体平均值为6.079×10-10cm/s。而RFC的渗透系数：1.990×10-10～4.01×10-8cm/s，变化较大，可能是由于试件形成方式对其影响导致。由①—④得到其总体平均值为8.899×10-9cm/s。

在现场试验中：由表8可知贵州5座水库RFC渗透系数相差不大，与省外一座水库计算渗透系数对比也相差不大，说明地区差异所造成RFC渗透系数变化较小，也进一步证实RFC渗透系数的数量级为5的可靠性。

由以上，得到6座水库RFC渗透系数的平均值为1.777×10-5cm/s，3座水库SCC渗透系数的平均值为3.899×10-6cm/s。

4.2 对比结果分析

(1)从室内、现场的总体平均渗透系数来看，两者存在差距，见表9。相关资料也指出室内和现场所得的渗透系数存在差异，对于碾压混凝土两者相差1～2个数量级[29- 30]。但从表9中可以看出SCC与RFC相差的数量级明显大于碾压混凝土。对于SCC，从表9可看出现场SCC与RFC渗透系数值相差不大，这可能是由于钻孔压水水时防渗层比较薄，笔者认为应参照室内的渗透系数。

对于RFC，笔者认为渗透系数相差较大的主要原因是室内、现场块石粒径差异大导致。虽然全集配混凝土试验有一定的代表性，试验结果应当与现场试验接近，但其与相对混凝土渗透试验结果接近，这需要进一步研究。但总的来说，目前现场压水得到的渗透系数有较大的可信度。

表9 总体平均渗透系数差异 单位：cm/s

(2)在1.2节中，对于现场压水试验计算渗透系数的公式较多，为比较公式之间的差异，通过采用文献[28]中坝顶段的6个钻孔压水数据进行计算，得到表10。从表10可以看出：式(8)计算结果较另外3个公式结果大，总体看差别不是太明显，但笔者还是建议采用理论较为清楚的式(3)或(9)进行计算。

5 结语

本文对堆石混凝土渗透系数的计算及试验方法进行了分析，提出了通过钻孔压水换算得到堆石混凝土的渗透系数，为堆石混凝土坝渗透系数的确定和渗透性能的评价提供参考价值。本文主要结论如下：

(1)从实际工程钻孔压水数据中得到的RFC重力坝坝体渗透系数总体平均值为1.968×10-5cm/s，其量级为1×10-5cm/s。对比室内渗透系数结果，相差4个数量级，较碾压混凝土所得的1～2个数量级高。导致差异较大的主要原因可能是：室内试件尺寸较小，块石粒径受限，而现场块石粒径大，两者骨料粒径悬殊差距所导致。对比目前的室内试验所得到的堆石混凝土渗透系数，笔者认为现场压水试验换算得到的渗透系数更具有代表性。

(2)基于现有测定渗透系数的常规试验设备来说，全集配混凝土渗透试验较为合适，而现场测定可采用钻孔压水试验。但两者所得的渗透系数结果差异还是较大，需要对全集配混凝土渗透试验进一步探究。

表10 现场公式计算值比较 单位：cm/s

(3)对于RFC渗透系数的计算，现场计算公式较多，建议采用式(3)或(9)试进行计算。