基于FGG NUFFT的穿墙成像雷达快速BP算法
李家强,陈焱博,徐才秀,陈金立,刘 然,朱艳萍
(1. 南京信息工程大学气象灾害预报预警与评估协同创新中心,江苏南京 210044;2. 南京信息工程大学电子与信息工程学院,江苏南京 210044;3. 江苏北斗卫星导航检测中心有限公司,江苏南京 210032)
0 引言
穿墙成像雷达(Through-Wall Imaging Radar, TWIR)利用电磁波良好的穿透特性,能够对建筑物、堡垒、草丛等隐蔽物后目标进行探测,其硬件成本低、质量轻、体积小、便携性好,并且能够进行实时目标定位、分类与识别,因此被广泛用于军用与民用领域,诸如执法行动、反恐斗争、刑事侦查、抢险救援等[1-5]。
穿墙雷达常用的成像方法有压缩感知(Compression Perception,CS)成像算法[6]、逆散射层析(Diffraction Tomography,DT)算法[7]、边界估计(Shape Estimation Algorithm Based on BST and Extraction of Directly Scattered,SEABED)算法[8]、后向投影(Back Projection,BP)算法[9]等。CS成像对稀疏或可压缩的回波信号,通过求解带约束的l1范数最优化问题,利用远低于Nyquist采样定理所需采样数重构原始回波信号成像,虽然CS成像应用前景广阔,但仍存在加性噪声和模型误差干扰求解过程以及图像结果等问题。DT算法能够对成像场景的图像准确重构,但其需要多次迭代运算,计算量巨大,在工程上难以应用。利用目标边界形状与接收脉冲延时之间存在逆边界散射变化的SEABED算法,可以对目标边界进行清晰成像,但存在障碍物时电磁波的传播路径和时延会发生变化,该算法不再满足逆边界散射变换,从而不能对目标进行精确成像。近年来,BP算法通过将雷达回波数据投影到成像区域的各个像素点,计算雷达回波在雷达天线和图像像素之间距离的时延,在时域上进行相干累加来实现高分辨率成像。由于BP算法计算过程简单易于工程实现,且能精确补偿墙体对信号产生的影响,因此被广泛应用于穿墙成像雷达中,但该算法运算数据量较大,存在冗余现象,从而导致计算复杂度较高,并且对计算机内存需求大,为此,国内外学者提出了一些相关加速BP算法的方法。文献[10]提出了一种快速因子分解后向投影算法,该方法将子孔径信号投影到局部极坐标下的成像网格上,通过距离维数的偏移和角度维数的旋转来校正得到粗糙的子图像,再将子图像进行融合得到最后的成像图,随后Moon等人提出了一种新的分解BP成像方法[11],该方法把图像分割成单独处理的列,将子图像连贯地相加。该算法容易实现并行化,由于每一列都可以独立于其他列形成,因此能够降低计算复杂度。以上方法都是通过分割子图像后进行融合,虽然在计算复杂度上有所降低,但同时也降低了成像精度。文献[12]提出了一种迭代子图像的BP成像算法,该方法迭代子图像进行图像重构降低复杂度,但不适用于大规模的雷达成像。文献[13]提出了一种快速BP算法,其原理是将成像区域分块划分,通过分级相干累加的方式减小BP算法的运算量,该算法虽然有效降低了一定的运算量,但是难以满足现阶段实时成像的需求。基于非均匀快速傅里叶变换的BP成像算法[14]利用BP算法中像素点幅值表达式满足非均匀傅里叶变换表达式,采用快速傅里叶变换进行计算,降低计算复杂度且保证成像质量,适用于大规模实时成像,但该算法需要重复计算幅值表达式中的系数,对计算机内存需求大。
针对上述问题,本文提出了一种基于快速高斯网格化的非均匀的快速傅里叶变换加速BP算法。该算法将BP算法中像素点幅值表达式与高斯核函数反卷积消除高斯平滑的影响,其次对均匀数据进行快速傅里叶变换,最后对得到的数据进行卷积运算平滑输出数据。仿真结果表明,所提算法能够避免重复计算和存储BP算法中像素点幅值表达式中的系数,从而快速计算像素点幅值矩阵,并且在不改变成像质量的同时,大大降低计算复杂度和内存需求,适用于大规模成像和实时处理。
1 穿墙雷达成像模型

图1 穿墙雷达探测场景模型
穿墙成像雷达模型如图1所示:前墙与后墙的墙体厚度为d,相对介电常数为εw,探测目标为半径r的理想电导体,置于两面墙之间,圆心与前墙的垂直距离为δ。设置平行于前墙体的两组间距极小的收发共置天线,其距离墙体分别为h1和h2,两组天线分别先后发射电磁波。电磁波首先穿透前墙体,经过墙体另一侧空气传播,到达目标物体后按原路散射回天线,两组天线具有相同的回波信号模型:
e(t)=et(t)+ew(t)+ea(t)
(1)
式中,et(t)为所需探测的目标信号,ew(t)为前墙体与后墙体的反射信号,假定天线为理想天线,那么噪声信号ea(t)=0。
2 基于FGG NUFFT的穿墙雷达快速BP成像
穿墙雷达探测过程中受墙体引起的强烈杂波信号干扰,往往目标信号会被淹没,无法进行目标检测及成像,因此成像之前必须通过算法消除墙体杂波信号的影响。
2.1 联合熵值法抑制墙体杂波
本文采用两组天线阵元分别平行于墙体进行全向扫描得到两组回波信号。对N个天线阵元回波信号分别进行采样,记采样次数为M,两组回波信号数据分别可组成M×N维矩阵e1,e2:
e1=[y1,y2,…,yN]
(2)
(3)

将式(2)与式(3)相加,能够得到
e=e1+e2=[z1,z2,…,zN]
(4)
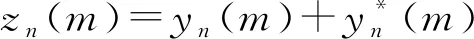
计算矩阵e1,e2中每个采样点值的概率:

n=1,2,…,N,m=1,2,…,M
(5)
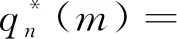
n=1,2,…,N,m=1,2,…,M
(6)
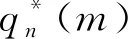
(7)
(8)
根据联合熵值定理[15],统计独立信源的联合熵值等于各信源熵之和,这里两组回波信号前后分别获得,可以视作相互独立,因此两者的联合熵值表示如下:
(9)
由于天线阵元不同扫描位置的变化,目标回波信号的变化强度较大,而墙体杂波的变化强度较小,因此目标回波信号熵值较小,墙体杂波熵值较大[16]。根据联合熵值定理[15],统计独立信源的联合熵值等于它们分别熵值之和,且大于其任何一个信源的熵值,即墙体杂波的联合熵值大于目标回波的联合熵值,可通过设置适当的门限值Z*能够滤除墙体杂波的影响,对回波数据e中每个元素进行处理:
Zn(m)=Z*·zn(m)
(10)
式中,Zn(m)为去除墙体杂波后所需的目标回波信号,而Z*定义为
(11)
式中,log(N)为联合熵值H的最大值,β为门限可调节因子,其调节范围为(0,2)。根据最大离散熵值定理[15],在离散信源等概率出现的情况下,信源的平均不确定性为最大,熵值将达到最大,即联合熵值取得最大值。
2.2 基于FGG NUFFT的快速BP成像
图2为穿墙雷达成像区域像素点网格化分,将整个探测场景划分为P个像素网格点,l1,l2,l3分别表示发射电磁波天线阵元与前墙体的斜距、电磁波在墙体传播的距离以及电磁波穿过墙体后到达目标的距离,则穿墙雷达BP成像可表示为
(12)
式中,I(xp,yp)为第p(p=1,2,…,P-1)个像素网格点的复幅度值,fm=f0+mΔf为第m(m=1,2,…,M)个工作频点,f0为发射信号的起始频率,Δf为频率间隔,τp为成像像素网格点p和第n(n=1,2,…,N)根天线之间的双程时延:
τp=2(l1+l3)/c+2l2/v
(13)
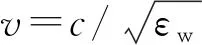
NUFFT能够直接对非均匀数据进行快速处理,即可将均匀采样数据变换到非均匀采样数据[17]。对于均匀采样序列F(k)∈C,k=0,1,…,K-1,K∈,则非均匀采样序列的离散傅里叶变换定义为
(14)
式中xj∈[0,2π]。gτ(x)是[0,2π]上的一维周期高斯核函数,其表达式如下:
(15)
式中,τ为高斯核函数参数,决定高斯核函数的指数衰减速率。
对高斯核函数gτ(x)进行傅里叶变换得到Gτ(k),令Gτ(k)与均匀数据F(k)反卷积消除高斯平滑的影响,得到辅助函数F-τ(k):
(16)
进一步对式(16)进行离散傅里叶反变换得到f-τ(x):
(17)
式中,Kr=R×K,Kr为过采样网格数,R为过采样系数。由于f-τ(x)满足均匀性,分布在均匀的网格点上,因此,可以用快速傅里叶变换对其进行计算。
对f-τ(x)进行卷积实现平滑输出,得到期望值f(xj):
f(xj)=f-τ*gτ(xj)=
(18)
在求解式(18)时,每次计算非均匀采样点xj时都要遍历所有的均匀网格点,因此计算量巨大,由于高斯函数的指数衰减特性,对远离xj的网格点忽略不计,因此可设置网格扩散范围,仅考虑xj附近的Ksp个点,Ksp为高斯核函数单边可延伸覆盖的网格点数量(Ksp=6表示单精度,Ksp=12表示双精度)。
式(18)中f-τ、gτ可表示为

(19)
(20)

E2·E3σ′·E4(σ′)
(21)
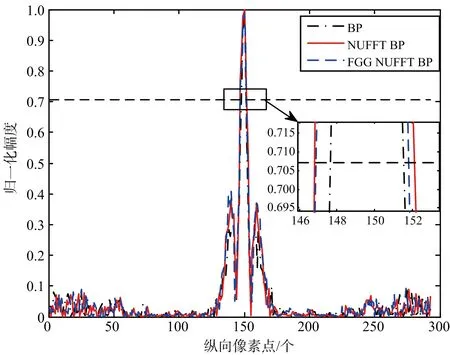
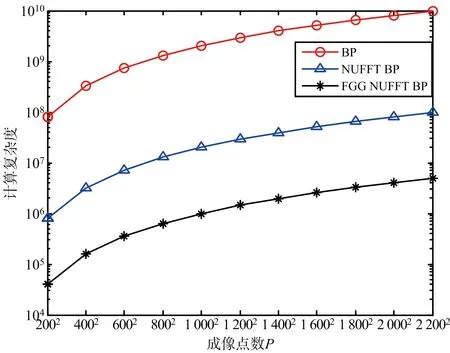
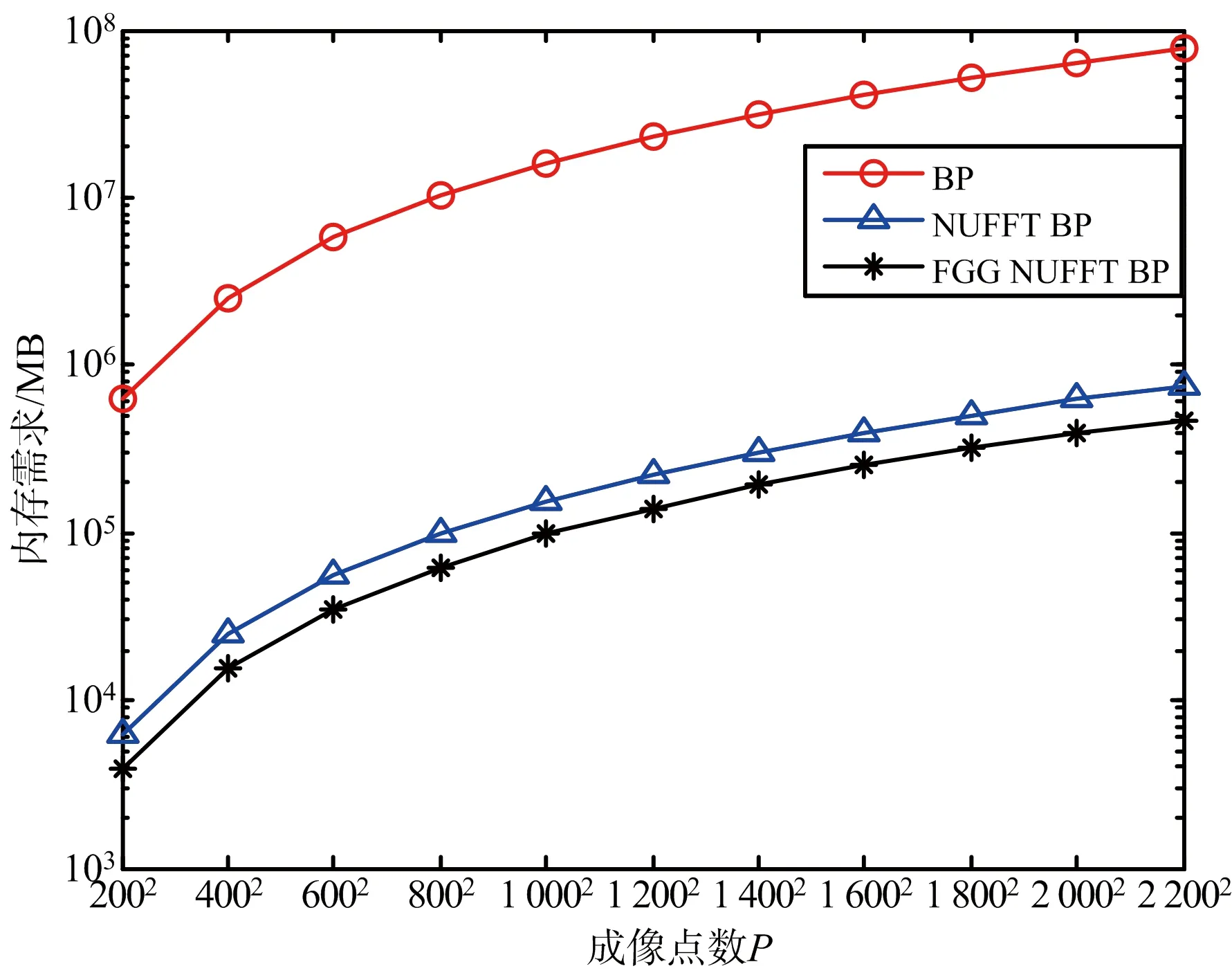
式中,-Ksp<σ′ 由于目标回波数据Zn(m)是均匀数据,时延τp对于单个像素点的幅值I(xp,yp)是非均匀的,无法直接用快速傅里叶变换进行计算,而本文所提FGG NUFFT算法适应非均匀性,能够对非均匀数据进行快速傅里叶变换。该算法的主要思想就是将均匀样本与高斯函数反卷积消除高斯平滑的影响,其次进行快速傅里叶变换,最后将样本卷积高斯函数实现平滑输出。因此,运用FGG NUFFT算法对像素点的幅值I(xp,yp)进行快速计算。 式(12)中BP成像算法可变形为 (22) 其中, (23) 式(23)能够通过FGG NUFFT来计算,式中每个像素点的幅值In(xp,yp)对应式(14)中的非均匀采样点f(xj),均匀目标回波数据Zn(m)对应式(14)中的均匀采样点F(k),频率间隔与双程时延的乘积2πΔfτp对应式(14)中的非均匀数据xj。 为了验证所提算法的有效性,本文利用基于FDTD的正演数值模拟软件GprMax2D/3D模拟穿墙雷达场景。模型设置如图1所示:天线阵元距离墙体分别为h1=0.05 m,h2=0.04 m;沿水平方向等间距扫描N=50次,扫描范围为0.1~2.1 m;天线发射电磁波的时间窗为24 ns。墙体为均匀介质,其厚度d=0.2 m,相对介电常数εw=6.4;理想电导体目标的半径r=0.1 m,其圆心距离墙体δ=1.0 m。图3为经过联合熵值抑制墙体杂波后得到的目标时域回波图。 (a) 基于BP算法成像 分别运用BP成像算法,NUFFT BP成像算法[17]和本文所提算法对穿墙雷达探测区域进行成像。选取电磁波频段范围为1~2 GHz,频率间隔Δf=0.49 MHz,频率点M=2 036。成像区域设置横向距离2.2 m,纵向距离2.1 m,按照横向的和纵向划分279×293个像素点。图4为3种算法的成像结果,其中图4(a)为基于BP算法成像、图4(b)为基于NUFFT BP算法成像、图4(c)为基于FGG NUFFT BP算法成像。为了比较3种算法的成像分辨率,对像素点矩阵进行归一化幅值,图5为3种算法的成像像素点归一化幅值曲线图。取成像最大幅值下降-3 dB处的像素点宽度,BP成像为3.8个像素点,NUFFT BP成像为5.3个像素点,本文算法成像为4.9个像素点,3种算法的宽度相差较小,均能对目标区域进行精确成像,且本文算法保持较好效果的同时优于NUFFT BP成像。 图5 成像点归一化幅值 分别对BP成像、NUFFT BP成像和本文提出算法成像的计算复杂度进行简要的分析。假设忽略天线根数的影响,取N=1,由于天线的采样点远远小于像素点个数,即M≪P。BP算法的计算复杂度为C0=MP,NUFFT BP的计算复杂度为C1=MlogM+|logε|P≈|logε|P,其中ε为理想计算精度[18-19]。本文设置高斯核函数单边可延伸覆盖6个网格点,即运算精度Ksp=6;过采样系数R=2,取值细节见文献[20]。本文所提的算法中E,E1,E2,E3,E4能预先被计算和存储,不需要重复计算,因此本文算法的计算复杂度为C2=(Ksp+1)M+(KrlogKr)+P≈P。图6为3种算法的计算复杂度与像素点网格点变化的曲线图,通过比较可以发现在同等条件下,对于同样的像素点本文算法计算复杂度要远低于其他两种算法计算复杂度,各类算法复杂度见表1。 表1 各类算法的计算复杂度比较 图6 计算复杂度 分别对BP成像、NUFFT BP成像和本文提出算法成像的内存需求进行简要的分析。实部和虚部都用浮点数表示,每个实部的内存需求为4 Byte,每个虚部的内存需求为8 Byte。BP的像素点幅值矩阵I∈CM×P,因此直接计算BP成像的内存需求为S0=8MP。 NUFFT BP成像的内存需求为S1=8(MlogM+|logε|P)≈8|logε|P。本文算法成像只需要存储系数E∈RP,E1∈C2Ksp×M,E2∈R2Ksp×P,E3∈R2Ksp×P,E4∈C2Ksp,则S2=4P(1+4Ksp)+8Ksp(1+2M)≈100P。图7为3种算法的内存需求与像素点网格点变化的曲线图,通过比较可以发现在同等条件下,对于同样的像素点本文算法内存需求要低于其他两种算法内存需求,各类算法内存需求见表2。 表2 各类算法的内存需求比较 图7 内存需求比较 传统的BP成像算法需要计算每个回波数据与图像像素之间双程并进行相干累加,因此存在计算复杂度高,内存需求量巨大,需要重复计算等问题。本文在对墙体杂波进行联合熵值法抑制的基础上,将FGG NUFFT算法运用到传统的BP成像中,首先将BP算法中像素点幅值表达式与高斯核函数反卷积消除高斯平滑的影响,其次对均匀数据进行快速傅里叶变换,最后对得到的数据进行卷积运算实现对数据均匀平滑输出。仿真实验结果表明,本文的方法在保证成像质量的情况下,解决了计算复杂度和内存需求随着工作频点、天线数量、像素点的增加而增加的问题,为穿墙雷达大规模成像与实时成像提供了新的思路与解决途径。3 实验结果与分析
3.1 穿墙雷达探测场景成像

3.2 计算复杂度分析

3.3 存储需求

4 结束语

