计及变压器铁芯饱和的LCC-HVDC输电系统谐波不稳定性评估与应用

刘 对，李晓华，蔡泽祥，蔡苏斌

（华南理工大学 电力学院，广东 广州510640）

0 引言

随着电力电子装备在电力系统中的广泛应用，谐波问题已成为电网中较为突出的问题之一［1］。作为电力电子技术的实际应用，基于电网换相换流器的高压直流（LCC-HVDC）输电系统谐波问题尤为严峻［2-4］。

近年来，电网中出现了多起因谐波导致直流保护误动的事件，严重影响了LCC-HVDC 输电系统的安全稳定性［3］。事故分析表明谐波经换流器及直流线路的转化、传递和放大后造成保护系统的误动。目前，已有文献针对LCC-HVDC 输电系统谐波进行了相应的研究。文献［5］对LCC-HVDC 输电系统变压器铁芯饱和的不稳定性问题进行研究，并且提出了稳定性的相应判据，但是该计算方法较为复杂；文献［6］提出了互补谐振的概念，分析了交、直流间相互影响产生的谐振。然而在实际LCC-HVDC输电系统中一旦发生谐波不稳定问题，上述2 种现象往往同时存在。文献［7］分析了不同短路比对谐波不稳定性的影响，其采用的频率扫描方法虽然可以得到计及换流器交流侧频率的阻抗特性但并不能揭示谐波不稳定性的产生机理。文献［8］通过时域仿真分析LCC-HVDC输电系统谐波，该方法计算准确，但时域仿真通常具有较大的计算量且效率较低。文献［9］利用开关函数对换流器的调制作用进行了相应的推导，并构建了LCC-HVDC 输电系统送端谐波不稳定问题的判据，然而在该判据中并没有考虑变压器铁芯饱和问题，具有一定的局限性。文献［10］在文献［9］的基础上加入变压器铁芯饱和因素，构建了更加贴近实际的谐波不稳定性判据。文献［11-13］利用文献［10］的判据分别研究了单一LCC-HVDC输电单侧系统、双回并行LCC-HVDC 输电系统以及多桥换流器LCC-HVDC 输电系统的谐波稳定性，并分析了影响谐波不稳定性的因素。文献［14］提出衰减因子来判断LCC-HVDC输电系统的谐波稳定性。然而文献［11-14］中的判据仅考虑了LCC-HVDC 输电系统的单侧换流器。由于LCC-HVDC输电系统通常包含送、受两端，每座换流站谐波的相互作用不仅受到自身的影响，还受到其他换流站影响，如果仅将某侧系统用一个理想电压源或电流源代替，通常会忽略其相应的阻抗频率特性对整个系统谐波不稳定性的影响。因此在分析LCC-HVDC输电系统谐波不稳定性时需要同时计及送、受两端的换流器对系统谐波不稳定性带来的影响［15］。文献［15］推导了同时考虑送、受端交流系统与直流系统间交互影响的LCCHVDC 输电系统的谐波不稳定性判据。该判据虽然同时考虑了送、受端交流系统与直流系统之间的影响，但在直流侧没有考虑平波电抗器及直流滤波器，且在直流线路方面考虑得过于简单，没有计及直流线路的耦合关系以及谐波在线路的传输与放大情况［16］。

鉴于此，本文基于端口理论建立了LCC-HVDC输电系统的谐波计算模型。该模型对LCC-HVDC输电系统进行了全系统建模，其中详细地介绍了变压器、换流器这2 个非线性设备的建模过程以及直流输电线路的线性传输模型。在该分析模型的基础上推导了基于2次谐波，并同时考虑送、受端交流系统与直流系统间交互影响以及变压器铁芯饱和的LCCHVDC 输电系统的谐波不稳定性判据。将该模型与基于PSCAD／EMTDC 的时域仿真结果进行对比分析，验证了所提方法的正确性。在不同运行工况及网络参数下利用该判据进行谐波稳定性判断，可用于LCC-HVDC 输电工程规划初期稳定性的评估，为直流的规划与运行提供了相应的参考。

1 LCC-HVDC输电系统谐波不稳定性机理及判据

LCC-HVDC输电系统通常包含整流侧、逆变侧2座换流站，每座换流站的谐波相互作用不仅受其自身的影响，而且受其他换流站的影响［15］。因此在分析LCC-HVDC输电系统谐波不稳定性时必须要考虑整流侧、逆变侧换流器对系统的影响。

1.1 LCC-HVDC输电系统谐波不稳定性机理

典型的LCC-HVDC 输电系统的结构见附录A 图A1。图中，Rgr、Rgi分别为整流侧、逆变侧的接地极电阻；Ri(i=1，2，3，4)、Ci(i=1，2，3，4)和Li(i = 1，2)分别为整流侧及逆变侧的电阻、电容和电感；L 为平波电抗器的电感；Qrj、Qij(j=1，2，3，…)分别为整流侧、逆变侧的断路器；Uac2、Iac2分别为交流系统的2 次谐波电压、电流；Yac2为交流侧的等效2 次导纳；Ycon2为从换流变压器端口看入的包含直流侧正序2 次谐波的等效导纳。

根据附录A 图A1，如果在换流器交流侧存在2次谐波电压扰动，该扰动电压经过换流器调制作用将在直流侧产生工频电压，从而在直流侧产生工频谐波电流；直流侧的工频电流经换流器调制后将在换流变压器阀侧产生正序2 次谐波电流分量和直流电流分量。而直流电流在流过换流变压器时可能会使变压器铁芯饱和，产生大量的各次谐波电流，包括正序2 次谐波电流。上述2 次谐波电流共同作用于换流变压器网侧2次谐波阻抗，产生正序2次谐波电压，从而形成1 个双向正反馈［5，15］，如附录A 图A2 所示。经过上述正反馈激励，谐波放大导致LCC-HVDC输电系统的谐波不稳定问题［15］。因此，在分析谐波不稳定性时重点需要解决变压器的饱和非线性、换流器的传递与放大以及直流输电线路的传输作用。

1.2 LCC-HVDC输电系统谐波不稳定性判据

利用电路的基本等效变化，附录A 图A1 所示输电系统可以等效为图1 所示电路，图中Is、V 分别为等效电流源、等效电压。

图1 交直流系统的等效并联电路Fig.1 Equivalent parallel circuit of AC／DC system

阻抗稳定性分析方法［17］的本质是将系统分为电源和负载子系统。电流源电流Is及交流系统导纳Yac2保持恒定，即：

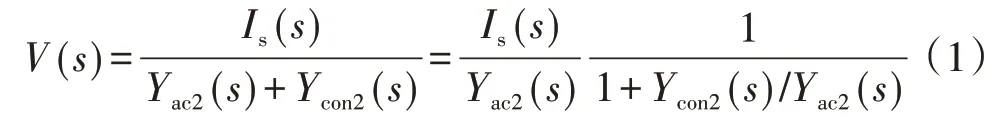
则系统的稳定性取决于传递函数G(s)：

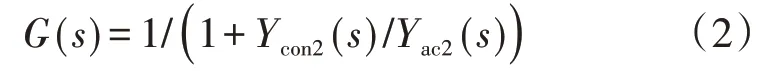
式（2）相当于包含1 个负反馈的闭环控制系统，该负反馈的前向通道增益是1，同时反馈通道增益为Ycon2(s)/Yac2(s)。根据线性控制理论分析可知，当Ycon2(s)/Yac2(s)满足奈奎斯特不稳定判据时，G(s)是不稳定的。则系统谐波不稳定的充要条件为：

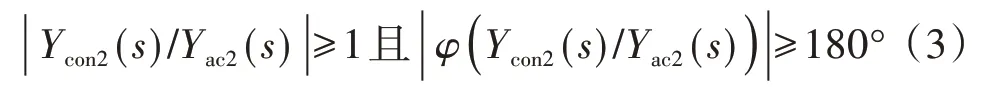
从上述判据中可以看出，判断谐波不稳定的关键在于得到从换流变压器端口看入的包含直流侧正序2 次谐波的等效导纳。而此部分包含了变压器、换流器、直流输电线路等直流输电系统的关键设备。鉴于此，本文采用端口等效模型计算等效导纳。

2 LCC-HVDC输电系统谐波建模关键技术

由附录A 图A1 可知，LCC-HVDC 输电系统可以分解为不同的部分，图中的虚线部分表示端口网络，则可得到LCC-HVDC 输电系统的等效端口原理图，如附录A 图A3所示。根据直流输电的原理，需将交流系统连接到端口的末端。为了得到LCC-HVDC输电系统的等效电路，需要对各部分进行建模，得到相应的端口网络。由于存在变压器铁芯饱和造成的非线性问题、换流器的非线性传递与放大作用及输电线路的传输作用这3 个方面的问题，需重点对LCCHVDC输电系统的这3个部分进行建模。

2.1 变压器等效模型

变压器是LCC-HVDC输电系统中不可缺少的设备。以Y-y 接线方式为例，换流变压器等效为二端口网络［18］，如图2 所示。图中，n 为变压器变比；IA、Ia和UA、Ua分别为变压器高压侧、低压侧电流和电压；XT为变压器等效电抗；TT为变压器等效矩阵。

图2 换流变压器的等效二端口网络Fig.2 Equivalent two-port network of converter transformer

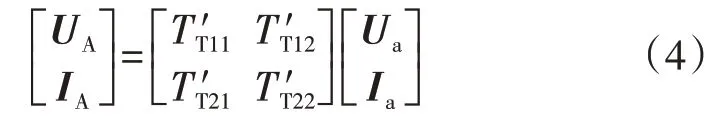
当考虑变压器的铁芯饱和造成的直流偏磁效应所产生的谐波电流分量时，需要对等效的端口矩阵进行修正。现有文献［19］已证明：随着绕组中注入直流电流的增加，励磁电流的各次谐波呈逐渐增长趋势，谐波次数越高，增长幅度越小。其中2 次谐波的线性程度最为明显且增长幅度明显高于其他各次谐波，因此本文着重考虑2次谐波分量的影响［19］。

仅考虑变压器铁芯饱和时，采用经验转换矩阵J 描述由于阀侧绕组直流电流注入而引起的正序2次谐波电流i0s2+［14］：

结合前文推导，考虑变压器的铁芯饱和造成直流偏磁效应所产生的2 次谐波电流分量修正公式见式（6），详细推导过程见附录B式（B3）—（B5）。

考虑变压器的铁芯饱和造成的直流偏磁效应所产生的2次谐波电流分量时，变压器的等效模型为：

2.2 换流器等效模型

换流器可以看作调制开关电路，用来连接直流系统和交流系统［20］。通过调制的开关函数能将交直流系统中的电压与电流进行相应的转换。直流系统存在的高次非特征谐波的幅值比低次小得多［21］，因此只考虑低次非特征谐波电压即可。

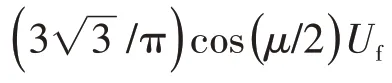
根据分析交流与直流的对应关系，利用交直流侧之间的关系式，当n=1时，可得换流器等效二端口电路的变换参数，详细推导见附录B式（B6）—（B8）。则换流器等效模型为：

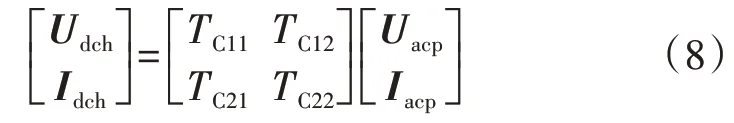
2.3 直流线路传输模型

实际的LCC-HVDC 输电线路通常为多条平行架设的导线组成，每条导线之间存在电磁耦合，电磁过程也较为复杂，求解时应先将其解耦。本文采用频率相关的模型［22］，以两相互感支路为例说明相间去互感原理，两相互感支路分别接于节点p、q 和节点r、w 之间，如图3 所示。图中，Zpq、Zrw和Ypq、Yrw分别为支路的自阻抗和自导纳；Zm、Ym分别为两相间互阻抗、互导纳；Ui(i=p，q，r，w)为节点电压；Irw、Ipq为支路电流。

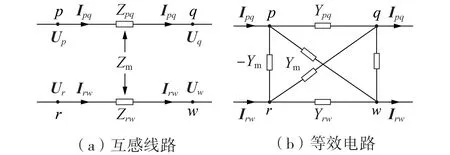
图3 两相互感支路及其等效电路Fig.3 Mutual inductance circuit and equivalent circuit of two phase inductance

图3（a）中2条互感支路的支路电压方程为：

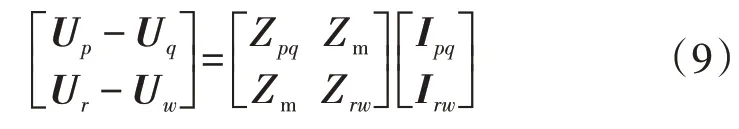
通过变换可以得到：

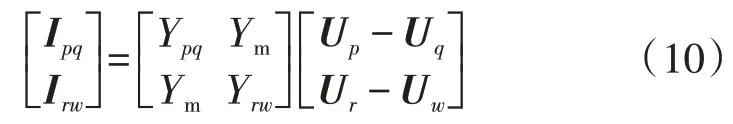
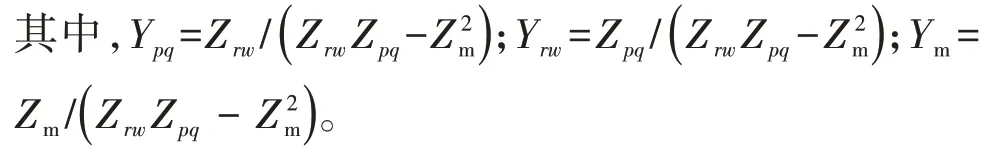
根据式（9）、（10）可得消去互感的无互感等效电路，如图3（b）所示。其由4 个节点和6 条支路组成，各支路导纳值分别为Ypq、Ym、Yrw。通过无互感的等值电路，可采用节点电压法列出对应的节点电压方程为：

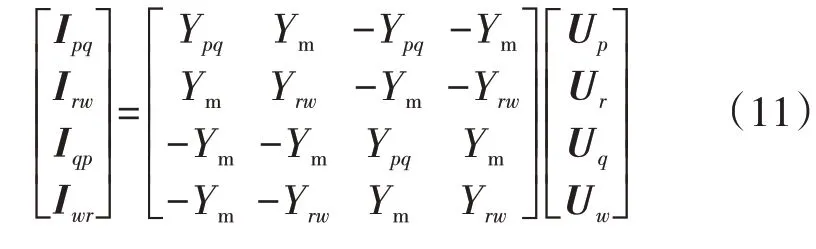
3 变压器和换流器的等效端口网络

变压器和换流器2 个端口的级联如图4 所示。图中，TT、TC分别为第一、第二端口网络的Τ 参数；T1为二端口网络级联后的Τ参数。

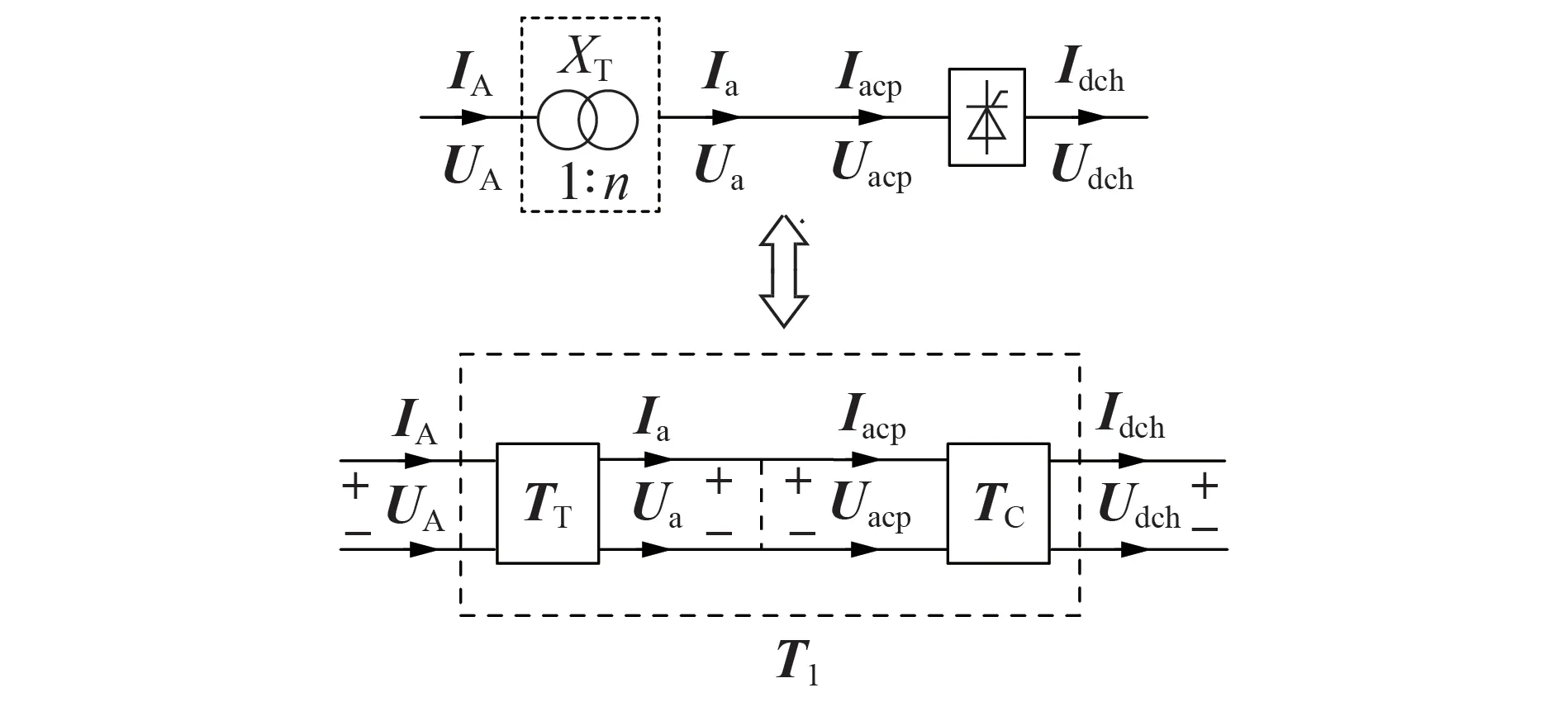
图4 端口级联Fig.4 Port network cascading

利用电路理论的基本原理［23］，可以得到2 个级联端口的等效表达式为：

即对于6 脉动的直流输电系统，可得变压器和换流器的等效端口参数。此外，12 脉动直流输电相当于2 个6 脉动系统的组合，如图5 所示，其左侧为并联，右侧为串联。

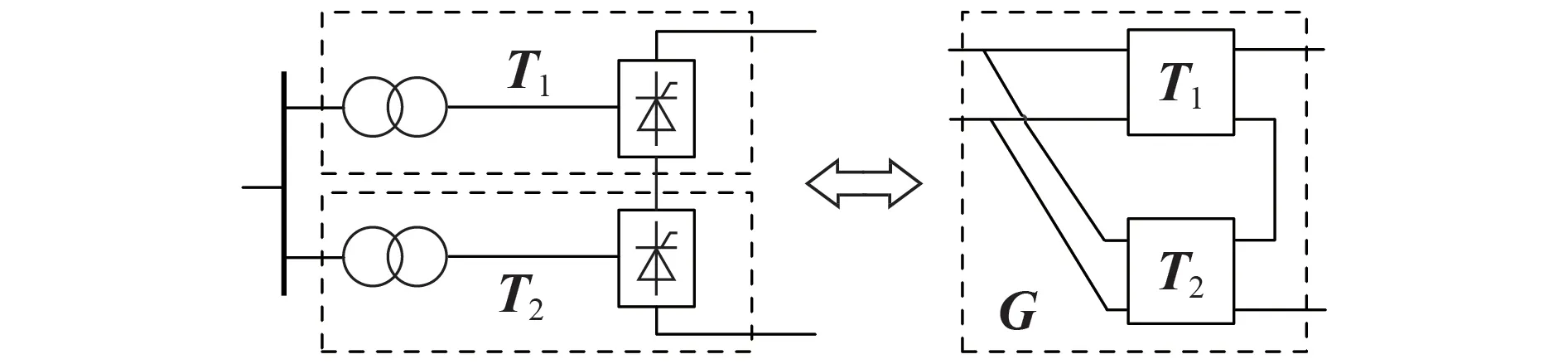
图5 串并联二端口网络Fig.5 Two-port network in parallel and in series

为了便于计算，必须将2 个端口的Τ 参数转换为对应的G 参数。假设端口网络的等效Τ 参数T0见式（13），则端口的等效G参数G0见式（14）。

其中，ΔT=TATD−TBTC，TA、TB、TC、TD为Τ 矩阵中的元素。

根据式（13）、（14），可得与12 脉动系统相对应的2 个端口网络的G 参数。2 个端口网络在左侧并联，在右侧串联，则连接参数见式（15）。

其中，G1、G2分别为矩阵T1、T2转化成的G矩阵参数。

逆变器端采用类似的方法，唯一的区别是端口连接方式不同。采用该网络参数来表征变压器和换流器的准确性见附录C表C1。

根据各部分的等效端口网络，可得整个直流输电系统的等效端口模型。如果交流侧存在谐波电压Uac2，采用等效端口模型可以计算出电流Iac2的大小，从而可以得到Ycon2=Iac2/Uac2。由于Yac2是已知的，这样结合式（3）就可以判断系统谐波的稳定性。

4 仿真分析

为了验证本文所提方法的正确性与有效性，将判据结果与PSCAD／EMTDC仿真结果进行对比。

4.1 LCC-HVDC输电系统仿真模型与谐波不稳定性仿真

利用PSCAD／EMTDC 电磁暂态仿真软件，基于CIGRE Benchmark标准测试系统［24］，结合文献［5］的测试系统搭建了如附录A 图A1 所示的双极1 000 MW 的LCC-HVDC 输 电 系 统 模 型。LCC-HVDC 直 流系统参数、交流系统参数见附录D 表D1，交流滤波器参数与文献［24］相同。系统运行稳定后，在整流侧交流母线上添加100 Hz 的电压扰动（0.1 s 后扰动消失）。若扰动消失后，直流电流不衰减，即认为LCC-HVDC输电系统发生谐波不稳定现象。

在PSCAD／EMTDC 电磁暂态仿真中，采用上述参数LCC-HVDC 输电系统的直流电流波形如图6 所示。从图中可以看出，直流系统的电流出现较大的振荡，不能恢复到原来的稳定状态，说明发生了谐波不稳定现象。

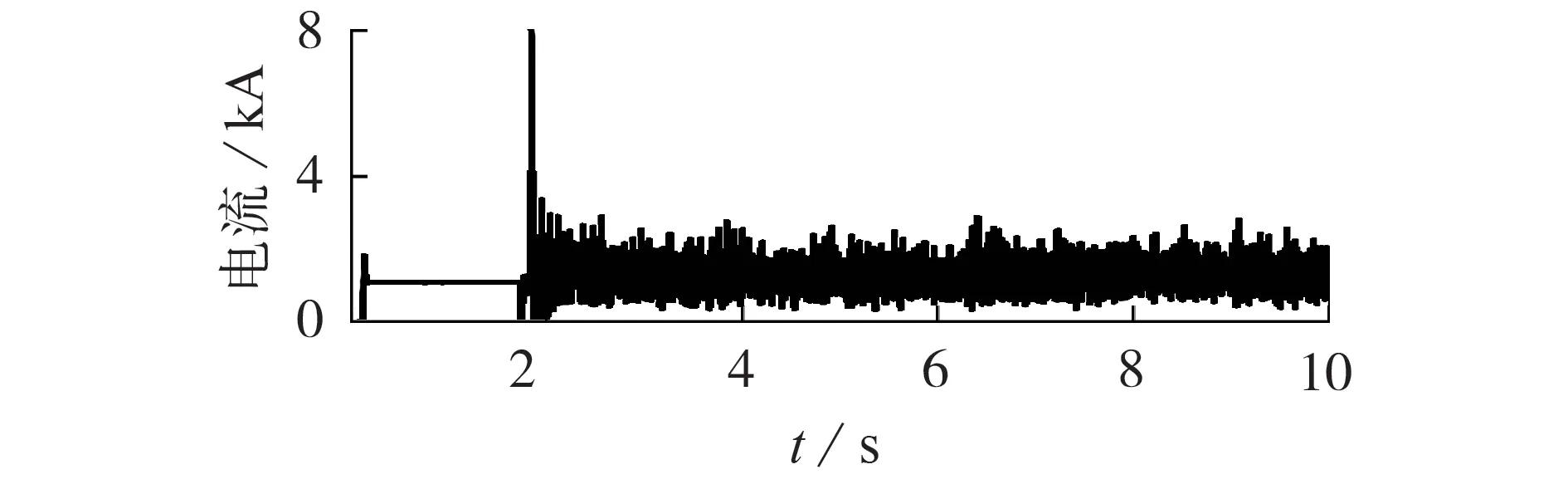
图6 LCC-HVDC输电系统的直流电流Fig.6 DC current in LCC-HVDC transmission system

同样，根据上述参数采用本文所提判据对LCCHVDC 输电系统进行谐波不稳定性判断；按照判据的计算步骤，分别计算出该算例在计及变压器铁芯饱和、不计及变压器铁芯饱和2种情况下的幅值ζ与相角δ参数，利用这2个参数值判别系统谐波的不稳定性。同时，结合在PSCAD／EMTDC 中记录的仿真波形进行验证。判据值与仿真结果如表1所示。

对比表1 中数据可以发现，在计及变压器铁芯饱和的情况下，本文的判断结果与PSCAD／EMTDC的仿真结果相吻合；而忽略变压器铁芯饱和时判断结果与仿真结果出现一定偏差，说明了计及变压器铁芯饱和的LCC-HVDC输电系统谐波不稳定性判断的准确性与有效性。

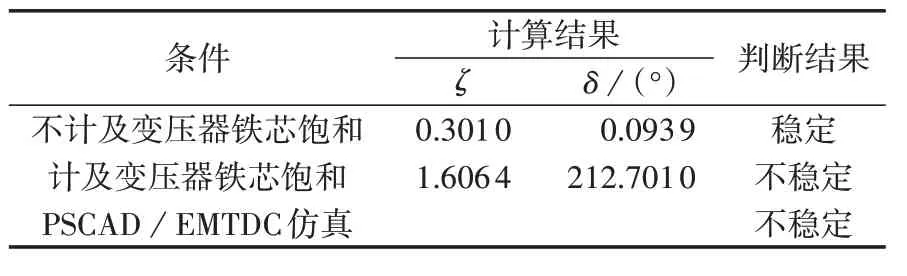
表1 谐波不稳定性判别值与仿真结果Table 1 Discriminant value of harmonic instability and simulative results

此外，从图6 及表1 中的结果可知：扰动电压在经过换流器调制作用后，在直流侧引起工频电压，进而在直流侧产生工频谐波电流；直流侧的工频电流经换流器调制后将在换流变压器阀侧产生正序2 次谐波电流分量和直流电流分量；而直流电流流过换流变压器使变压器铁芯饱和，产生正序2 次谐波电流；上述正序2 次谐波电流分量共同作用于换流变压器网侧2 次谐波阻抗，并产生正序2 次谐波电压，从而形成了一个双向正反馈，导致谐波不稳定。

4.2 LCC-HVDC输电系统谐波不稳定性的影响因素

在不同的运行工况以及网络参数（给出的参数为相应改变量）下利用该判据进行谐波不稳定性判断，并与PSCAD／EMTDC 仿真平台中建立的验证模型仿真结果进行对比，对比结果见附录E 表E1。所设置的仿真算例参数及算例仿真波形见附录E 图E1。通过表E1的分析结果可知，不计及变压器铁芯饱和时判别结果与实际情况相比存在一定的误差；而计及变压器铁芯饱和时判别结果与实际仿真结果基本一致。这也说明了本文方法的准确性与有效性。下面将针对附录A 图A1 所示的系统从不同方面进行谐波不稳定影响因素分析。

4.2.1 送端系统对谐波不稳定性的影响

算例1、2 在附录D 表D1 参数所示的算例（后文将称为基本算例）的基础上，修改电阻参数R1进行验证。对比这3 个算例可以发现，在减小送端系统的R1时，系统发生谐波不稳定现象。算例3、4 在基本算例的基础上修改电容参数C1进行验证，同样对比这3 个算例可以发现，在减小送端系统C1时，系统出现谐波不稳定现象。上述算例表明送端系统的阻抗值对系统的谐波稳定性有较大的影响。在实际工程设计中可通过合理设计送端系统参数，避免系统不稳定现象的发生。

4.2.2 直流平波电抗器对谐波不稳定性的影响

算例5、6 在基本算例的基础上修改直流系统的平波电抗器电感值进行验证，对比这3 个算例可知，平波电抗器对LCC-HVDC输电系统的谐波稳定性同样具有一定的影响。在减小平波电抗器电感值的过程中，系统会发生谐波不稳定现象。因此，在选择平波电抗器时应计及其平波的效果与直流动态响应性能等因素加以权衡。

4.2.3 受端系统对谐波不稳定性的影响

算例7—10为受端系统参数R3、C3变化的结果，通过分析可以发现，受端系统对谐波稳定性有较大的影响，且其影响关系与送端系统表现出一定的差异性；故仅考虑直流输电系统单端的谐波不稳定判据将会具有一定的片面性，应综合考虑送、受端共同影响且更加贴近工程实用的谐波不稳定性判据。

4.2.4 传输功率对谐波不稳定性的影响

算例11、12 在基本算例的基础上修改直流传输功率进行验证。对比这3 个算例的结果可知，降低直流系统的传输功率有利于减小谐波对系统稳定的影响，因此在LCC-HVDC 输电系统运行过程中发生谐波不稳定现象时，可降低传输功率以提高系统的稳定性。

5 结论

针对LCC-HVDC 输电系统的谐波不稳定问题，本文基于端口理论建立了LCC-HVDC输电系统的完整端口模型，重点介绍了变压器、换流器这2 个非线性设备的建模过程以及直流输电线路的线性传输模型。该端口模型综合考虑了直流系统两端变压器、换流器、平波电抗器以及交流滤波器的影响，并在此基础上构建了谐波不稳定性判据。在不同的运行工况以及网络参数下进行谐波稳定性判断，并与PSCAD／EMTDC仿真结果进行对比，结果表明：

（1）本文基于端口模型构建的计及变压器铁芯饱和的判据判别结果与电磁暂态仿真结果相吻合，说明了本文方法的准确性与有效性；

（2）该判据能用于评估LCC-HVDC 输电系统谐波不稳定性风险，对影响因素的分析可以为LCCHVDC 输电系统的设计以及避免运行阶段谐波不稳定现象的发生提供相应参考；

（3）本文提出的计及变压器铁芯饱和的LCCHVDC 输电系统谐波不稳定性评估方法可以推广应用到更复杂的多端高压直流输电系统中。

本文所提的判据由于没有考虑直流控制系统的影响而存在一定的误差，后续研究将集中在控制系统对LCC-HVDC输电系统的影响方面开展。

附录见本刊网络版（http：//www.epae.cn）。