基于系统动力学的干旱区植被生态需水量预测算法

曹晓磊

(河北省石家庄水文勘测研究中心，河北 石家庄 050051)

在所有的生态环境危机中，对人类生产和生活有重大影响的问题就是水资源问题，水资源作为可持续利用资源，支撑着所有生命[1]。在人们的生活中对于水资源的利用应做到不影响生态系统的可持续性，如果忽视生态系统与水资源之间关系，将直接导致森林退化、生态环境恶化等诸多问题[2-4]。特别是干旱区域，由于干旱地区降水稀少，可利用的水资源比较少，研究该地区的植被生态需水量有着重要意义[5]。

植被作为生态系统中的生产者，对维持生态平衡有很大作用，对于干旱地区的生态建设首先需要解决的就是植被需水问题[6]。在20世纪80年代初期美国研究的生态和环境需水分析已初具雏形；90年代后，在许多专家学者和研究机构的研究下，针对不同类型的生态系统，分析植被和水资源利用之间的相互关系，推动了生态环境和植被需水量的研究与发展。国内的研究中，对于植被生态需水量的研究还不够深入，从目前的研究现状可知，现阶段对于干旱区植被需水量的预测还没有特别成熟的技术，使用的较为常见的预测算法有基于水量平衡的需水量预测算法和基于分数阶灰色模型的需水量预测算法。以上两种预测算法在实际应用中，并没有将各个变量之间的反馈关系考虑到，导致算法可靠性差，预测结果不能满足生态环境发展策略，算法经济效益低、污染负荷大。因此，研究基于系统动力学的干旱区生态需水量预测算法，利用系统动力学模型建立能够表现出水资源配置的模型，预测出需水量最优解，解决传统算法中存在的问题。

1 基于系统动力学的干旱区植被生态需水

量预测算法设计

1.1 建立水资源动力学模型

干旱区植被生态需水量的预测与该地区整个水资源的配置有紧密联系，利用系统动力学建立水资源动力学模型，将具有因果关系的要素通过箭头的形式连接起来，形成因果反馈回路图，表示出水资源动力学模型内部各部分之间的关系。水资源因果关系反馈回路如图1所示。

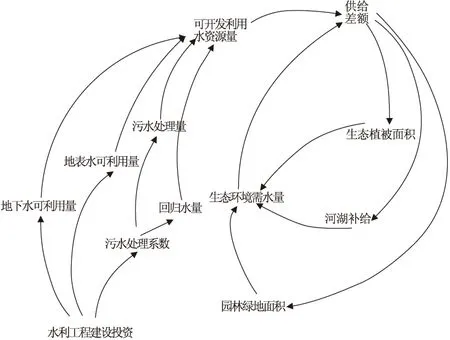
图1 因果关系反馈回路图

根据图1中显示的因果关系，建立水资源供给子模型。水资源供给子模型主要包括地表水、地下水可供水资源量、污水处理量和回归水量。相关的系统动力学方程如下：

W地表=Lookkupfunction1(time)

(1)

W地下=Lookkupfunction2(time)

(2)

Whg=Wws×αhg

(3)

Wws=Wsh+Wgy

(4)

以上方程中Wdb表示地表水量；Wdx表示地下水量；Whg表示回归水量；Wws表示污水处理量；Wsh和Wgy分别表示生活和工业上的污水处理量；αhg表示回归系数。生态环境需水量子模型相关参数为园林绿化用水量、湖泊补给量、水面蒸发量和植物蒸腾量。相关系统动力学方程为：

Mhp=Mzf+Mzt

(5)

Mlh=Mld-Whg

(6)

上列方程中Mhp表示湖泊补给量；Mzf表示水面蒸发量；Mzt表示植物蒸腾量；Mlh表示园林绿化用水量；Mld表示绿地用水量。将水资源供给子模型和生态环境需水量子模型结合在一起，建立水资源动力学模型，利用水资源动力学模型预测干旱区植被生态需水量。

1.2 计算生态需水量相关参数

使用CN3型传感器测定土壤热通量和土壤温度，传感器探头分别安置在地表不同埋深距离处，每隔一分钟采集一组数据，自动保存干旱地区的土壤数据。传感器布置如图2所示。

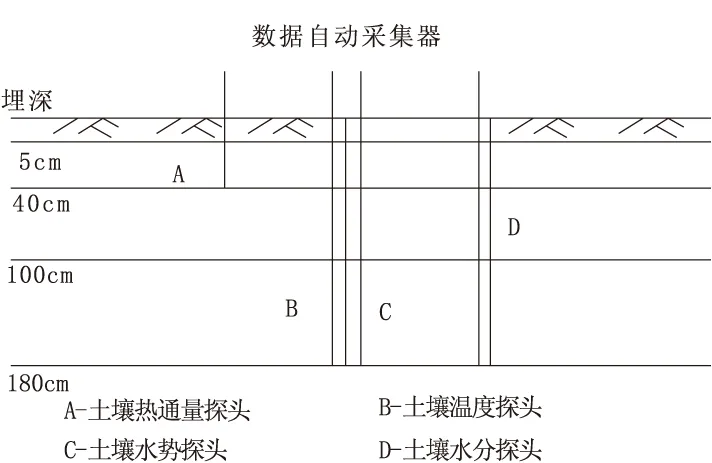
图2 土壤参数测量装置布置示意图

同理测定土壤水分和土壤蒸发量。根据测定的相关参数，确定蒸发系数与埋深的关系为：

mc=0.50exp(-2.11L)

(7)

式中：mc表示蒸发系数；L表示埋深距离。

测定的土壤水分蒸发量见表1所示。

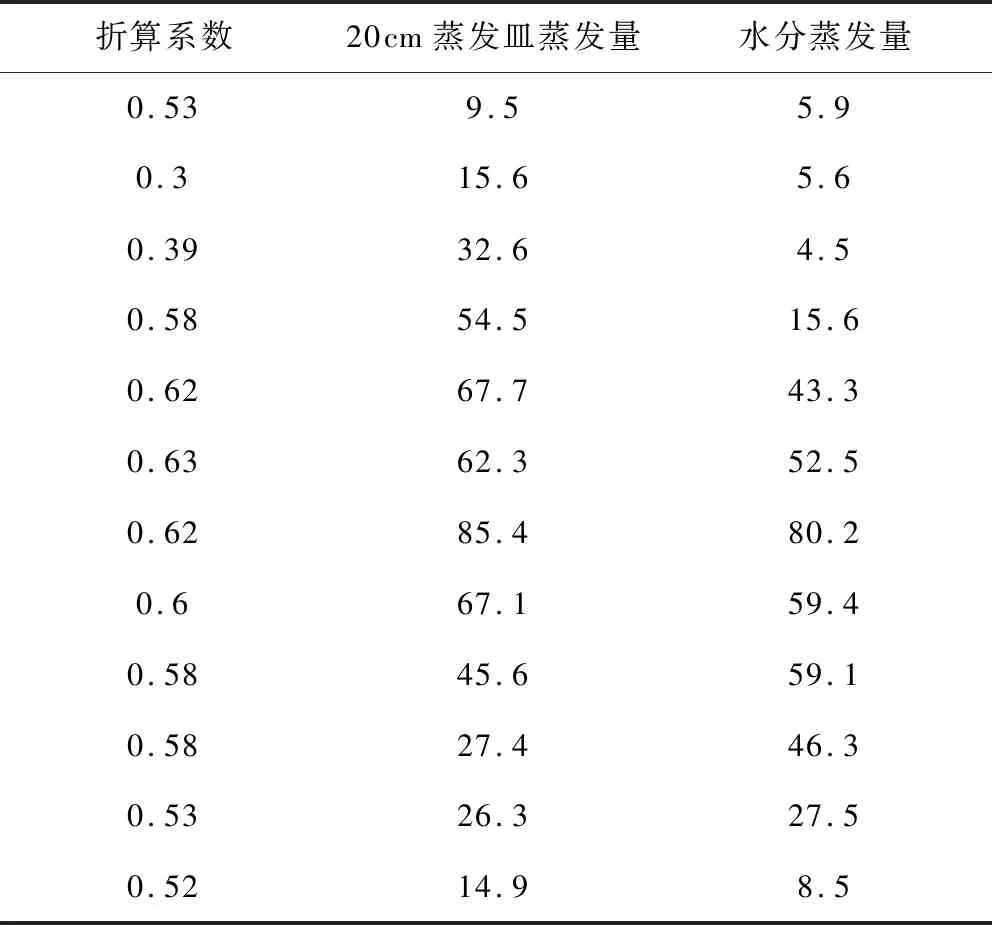
表1 土壤水分蒸发量

通过折算系数可知植被生长状况比较好的情况下，植被系数φ与埋深的关系：

φ=2.52exp(-0.174L)

(8)

对于比较稀疏的植被，需要根据盖度进行修正，修正后的植被系数为：

φc=1+λ[2.52exp(-0.174L)-1]

(9)

公式中λ表示修正系数，当植被系数等于1时，修正系数为0，反之修正系数等于1。根据干旱区不同植被类型的盖度确定修正系数。如表2所示。

表2 不同类型植被的修正系数

通过以上过程确定蒸发系数和植被系数，利用这两个系数预测干旱区植被生态需水量。

1.3 预测干旱区植被生态需水量

在给定气候条件下，以保证干旱区具备适宜土壤水分，使植被达到完全生产能力为目的，计算植被蒸散量：

Mzt=φcmc

(10)

式中：φc表示作物系数；mc表示参考作物蒸腾量。在非标准情况下，土壤含水量会影响植被生长状况，当土壤含水量低于阈值，植被受到水分的胁迫。植被受到影响的程度主要由土壤水分限制系数决定，在这种情况下，植被蒸散量的计算公式为：

Mzt-a=φtφcmc

(11)

式中：Mzt-a表示非标准条件下的植被蒸散量，mm/d；φt表示土壤水分限制系数。在干旱地区，降雨量稀少，土壤水分不能达到植被最适合的程度，在这种情况下，植被覆盖率低。面对非完全覆盖的天然植被，生态需水量的预测需要在非标准情况下进行，假设不同种类植被的覆盖面积为Sp，则植被生态需水量预测结果为：

M0=Spφtφcmc×10-3

(12)

式中：Sp表示植被分布面积，单位为m2。通过以上公式即可预测出干旱区植被生态需水量，基于系统动力学的干旱区植被生态需水量预测算法设计完成。

2 干旱区植被生态需水量预测算法实验研究

2.1 实验准备

在干旱区植被生态量预测算法实验中，需要大量的空间数据和属性数据，利用GIS软件对选择的实验区域进行投影变换等操作，转换成需水量预测所需要的Grid格式，根据实验地区的实际情况，建立需水量预测算法需要的属性数据库。转换后的实验区域内土壤粒径组成如表1所示。

基于以上数据，以经济效益和污染负荷作为研究目标，设计对比实验，主要验证不同预测算法的实际应用水平。

2.2 经济效益实验及分析

实验中使用天气发生器模拟实际的天气，输入的数据以实际干旱地区的每月气象数据为主。实验结果如下所示。

表4中显示的经济成本是在预测结果的基础上进行水资源规划所需要的成本，表中算法1为基于水量平衡的预测算法，算法2表示基于分数阶灰色模型的预测算法，算法3为基于系统动力学的预测算法。从表中结果可以看出，当月降雨量大于月蒸发量时，需要消耗的成本为负数，三组结果对比来看，在月降雨量小于蒸发量时，所需要的经济成本最少，在月降雨量大于蒸发量时，带来的经济效益最高。综上所述，设计的基于系统动力学的干旱区植被生态需水量预测算法经济效益更高。

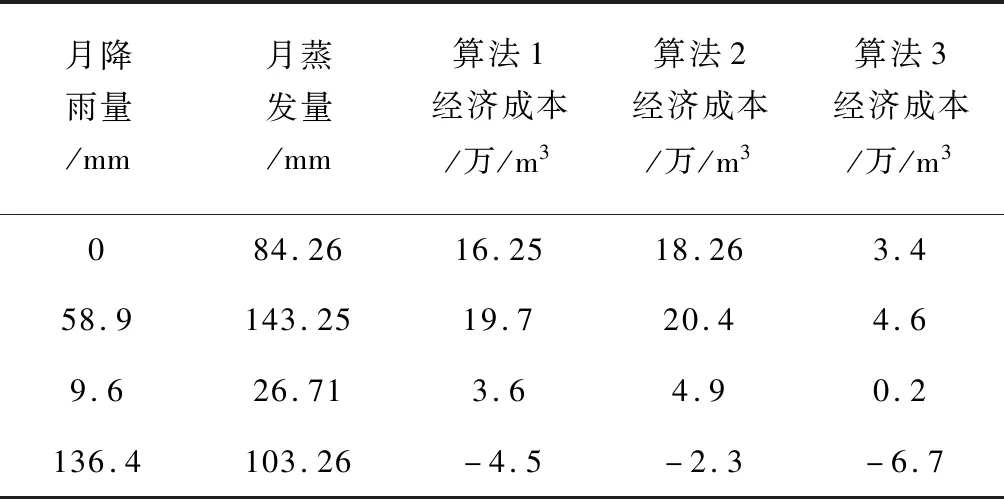
表4 不同预测算法经济效益实验结果

2.3 污染负荷实验及分析

干旱地区的污染来源主要包括点源污染和非点源污染，点源污染主要是排放出的污染气体，这种污染已经得到了控制；非点源污染主要包括农业施肥、农药的使用等造成的污染。因此，在污染负荷实验中，主要是使用不同的预测算法，基于表3中数据，根据预测结果获得实验区域的污染负荷情况。实验结果如图3所示。

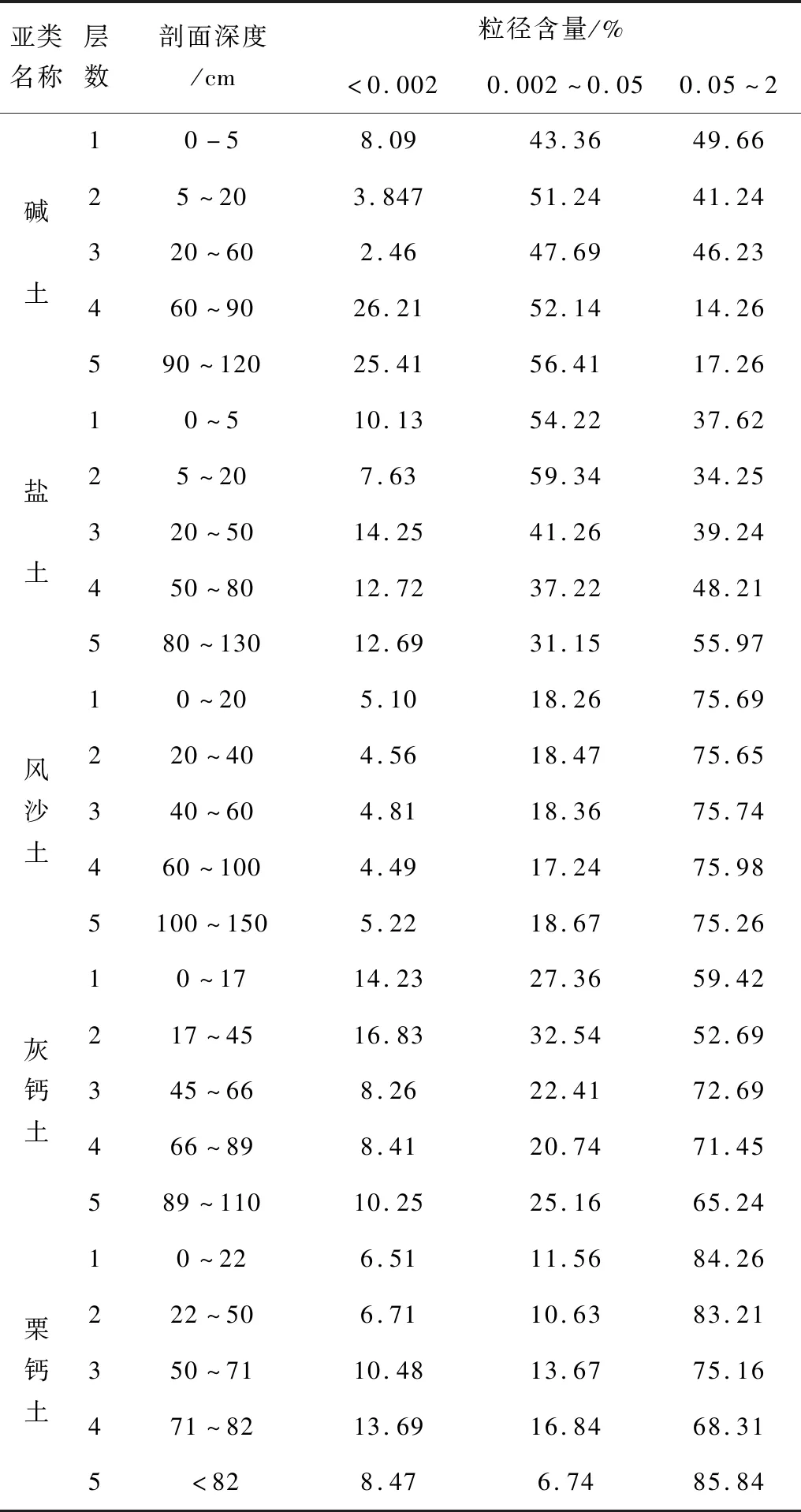
表3 实验区域的土壤粒径组成

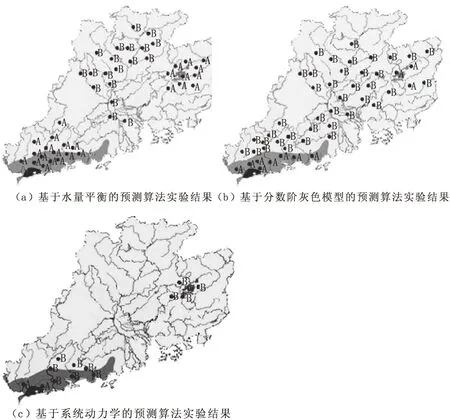
图3 不同预测算法的污染负荷实验结果

图中显示的深色为比较严重的干旱地区，浅色地区表示半干旱地区，标记A表示污染负荷高，标记B表示污染负荷低。对比观察图中结果，从中可以看出，图a中结果污染情况相对集中，在干旱区污染负荷较高，在其它区域污染负荷低；图b中结果显示，污染情况比较分散，干旱区污染负荷高、半干旱区污染负荷较低，整体污染范围比较广；图c中显示，污染范围较小，只在小区域内存在，从整体上看，污染负荷比较低，污染程度在可控范围内。结合经济效益实验结果可知，设计的基于系统动力学的干旱区植被生态需水量预测算法经济效益高、污染负荷少，符合生态环境发展的策略，该算法优于传统的植被需水量预测算法。

3 结语

在干旱地区，植被通常不能将土壤表面完全覆盖，在干旱季节更为严重。本文结合干旱区土壤和水文观测资料，设计基于系统动力学的干旱区植被生态需水量预测算法。利用系统动力学建立水资源动力模型，挖掘出更深层次的因果关系，为后续植被生态需水量的预测提供强有力的支撑。通过设计的对比实验，验证了设计的预测算法解决了传统算法中存在的问题。但是由于时间、数据等条件的限制，在确定参数过程中，没有对参数的精度进行处理，这可能对最后的植被生态需水量的预测产生一些影响，希望在后续的研究中，能够对这一方面重点展开，为干旱区植被生态需水量的预测提供更好的预测结果，满足更高的精度需求。