Spatial heterogeneity of dead fuel moisture content in a Larix gmelinii forest in Inner Mongolia using geostatistics

Heng Zhang · Shihao Ma · Ping Kang · Qiuliang Zhang · Zhiwei Wu

Abstract Spatial heterogeneity of fuel moisture content determines the spread rate and direction of a forest fire. Research on the spatial heterogeneity of the moisture content of dead fuel of Larix gmelinii Rupr. showed that: (1) fuel moisture content in litter layer < semi-humus layer < humus layer, and the coeffi cient of variation decreased with sampling depth; (2) the sill value of the semi-humus layer was highest, the humus layer moderate, the litter layer the smallest, overall, the spatial heterogeneity of the semi-humus layer was the highest. The humus layer in the slant direction and three layers in a vertical direction showed strong spatial correlation with the lowest nugget coeffi cient of 0.0968; (3) the fuel moisture content of the humus layer showed strong spatial anisotropy; and, (4) estimating the total moisture content of the sampling site by stimulated sampling reasonable control of the sampling interval, and increasing the sampling intensity can reduce the error. When the sampling intensity is increased to more than 16 and the sampling interval 3 m, the standard error is < 15%. The spatial heterogeneity of fuel moisture content is best revealed by increasing sampling density, sampling in different fire seasons, and in different slope directions and positions. The results can provide a scientific basis for forest fire prediction and prevention.

Keywords Forest combustibles · Spatial heterogeneity · Analog sampling · Standard error

Introduction

The moisture content of forest fuels determines the diffi culty of fire control and rate of spread (Li et al. 2015) and is a key factor in fire risk and fire behavior prediction (Zhang et al. 2018). It has strong spatial heterogeneity, i.e. horizontal and vertical distribution, and will change the distribution of fire spread rate and direction (Wang et al. 2012). To accurately estimate the probability of the occurrence of forest fires and the spatial characteristics of fire spread, understanding fuel moisture content and its spatial heterogeneity is necessary. Spatial heterogeneity refers to the complexity and variability of system or system elements, including the spatial composition, configuration and correlation of system elements (Bi et al. 2006). Geostatistics is an effective tool for studying spatial heterogeneity ofenvironmental factors and was first proposed in the 1960s (Matheron 1963). It was first applied in the mining and petroleum sectors (Zhang et al. 2009) and widely used in the analysis of spatial patterns ofenvironmental factors and simulation ofecological processes, especially in geology, ecology, water resources and soil science (Wang et al. 2001). In recent years, there have been studies of spatial heterogeneity using geostatistics (Shi 2012; Jing et al. 2016), mainly of soil nutrients and soil water content (Liu 2013; Fu et al. 2014; Zhang 2016; Song et al. 2019). There have been few studies on the spatial heterogeneity of water content of forest fuels. Ivanov et al. ( 2010) studied the spatial heterogeneity of soil water and found that its heterogeneity index had a lag dependence on the average water content. This characteristics can inhibit the spatial heterogeneity of soil water after rainfall affected by topography, thereby enhancing the spatial heterogeneity of soil content. In terms of the spatial heterogeneity of the moisture content of forest fuels, field sampling intervals and methods have considerable impact on the estimation of fuel moisture content. Mao et al. ( 2012) noted that it was important to determine the appropriate sampling interval and sampling method for reducing errors. Ettema and Wardle ( 2002) analyzed using geostatistics how the spatial distribution of soil organisms affected plant growth and plant community structure. The results were dependent on the spatial resolution as defined by sample size, sampling interval, and analysis variables. Liu and Shao ( 2012) studied the spatial heterogeneity of soil water content in reclaimed grasslands in the loess area, and analyzed the impact of sampling interval and concluded that a small sampling interval could represent the real spatial heterogeneity of soil water content, but with an increase of sampling interval, the variation of spatial heterogeneity smaller than the sampling scale may be hidden. Traditional statistical methods are diffi cult to spatially characterize the impact of field sampling intervals and methods on the estimation of fuel moisture content. In contrast, geostatistics can effectively address this problem.

In this study, the dead fuel of a Larix gmelinii forest in the Saihanwula Nature Reserve was sampled in the litter layer, semi-humus layer, and humus layer in three directions to measure moisture content. Geostatistics was used (1) to reveal the spatial heterogeneity of the dead fuel moisture content and to analyze factors influencing spatial heterogeneity; and (2) to estimate total water content of the sample area by simulated sampling and to analyze the influence of sampling interval and sampling intensity on the standard error of the moisture content, making the statistical data closer to reality. The results of this study will be important for preventing forest fires and for understanding the dynamics between surface and underground fires.

Materials and methods

Study area

The Inner Mongolia Saihanwula Nature Reserve is in the northern part of the Bahrain Right Banner, Chifeng City, Inner Mongolia Autonomous Region, China (118° 18′–118° 55′ E, 43° 59′–44° 27′ N) (Fig.1). The average elevation is 1000 m.a.s.l., and the climate is mid-temperate semi humid. Annual average precipitation is approximately 400 mm, annual average temperature is 2 °C (Yan et al. 2017). The area belongs to the forest steppe ecotone with the vegetation dominated byforests with a coverage of 61.9%. The main tree species are Xing’an larch ( Larix gmelinii), aspen ( Populus davidiana Dode), white birch ( Betula platyphylla Sukaczev) and Mongolian oak ( Quercus mongolica Fisch. ex Ledeb.) (Zhang et al. 2008).

Fig.1 Location of the study area

Field sampling

During the autumn fire prevention period in mid-September 2017, a typical area of a Larix gmelinii forest was selected in the Reserve and a 100 m × 100 m sample area established on a sunny slope at 1890 m.a.s.l. Three transects were taken in three directions: V (vertical) transect was from the top to the bottom of the slope, H (horizontal) transect was perpendicular to it, and O transect was on the angle between them. The length of each transect was 96 m, the distance between the two points of the first 20 points was 0.3 m, 6 m in total, the distance between the two points of the last 60 points was 1.5 m, 90 m in total in three directions (Fig.2). In the absence of precipitation for five consecutive days, three layers—litter layer, semi-humus layer and humus layer, were sampled in three directions, one sample from each sampling point, numbered and weighed (wet weight) on site, placed in an envelope and taken to the laboratory for drying.

Calculation of fuel moisture content

Samples were dried to a constant weight after 8 h at 105 °C, and the moisture content in each layer was calculated using the following formula:where M is the absolute fuel moisture content (%), WHthe fuel wet weight (g), WDthe fuel dry weight (g).

Fig.2 Schematic diagram of the sampling site

After calculating the fuel moisture content, the maximum, mean, variance, standard deviation and coeffi cient of variation of the moisture content were analyzed to reveal spatial heterogeneity.

Calculation of spatial heterogeneity of fuel moisture content

Heterogeneity is the product of continuous interaction of basic ecological and physical environmental processes on spatial and temporal scales (Han and Wang 2002). A semivariogram is a graph of how semi-variance changes as the distance between observations changes. In this study, semivariogram analysis and GS + 9.0 geostatistical analysis software were used to establish the theoretical model of the semivariogram. The moisture content and its spatial heterogeneity are described by the sill value (value on the y-axis), nugget coeffi cients and fractal dimensions.

The variation function describes the spatial heterogeneity of the moisture content, indicating changes at different sampling intervals. The calculation formula is:

where γ( h) is the semivariogram; N( h) is the sample logarithm at a sampling interval of h; Z is the regionalized random variable; Z( xi) and Z( xi+ h) are measured values of moisture content at xiand xi+ h, respectively.

Semivariogram models include spherical, exponential, Gaussian, and linear (Hernandez-Stefanoni and Ponce-Hernandez 2006). In this study, the dead fuel moisture content and sampling interval were fitted with spherical, exponential, Gaussian and linear semivariogram models. Figure 3 is a schematic diagram of an ideal semivariogram curve.

Fig.3 Schematic diagram of an ideal semivariogram curve

a is the sampling interval at which the variation reaches the sill value, indicating the spatial correlation scale of the random variables; when h ≤a , any two points have a correlation and the correlation decrease with the increase of h; when h > a, there is no correlation (Bi et al. 2006); C0is the nugget value, indicating when h is very small, the change in values between two points reflect the possibility of the randomness within the regionalized variables Z( x); C1is arch height, indicating the spatial heterogeneity caused by correlation factors (Li et al. 2012); C0+ C1is the sill value, indicating the intensity of variations of regionalized variables within the scope of this study is the largest variation of the observed indicators; the greater the value, the higher the degree ofoverall spatial heterogeneity (Hao 2005); C0/( C0+ C1) is the nugget coeffi cient, indicating the degree of spatial correlation of system variables. The nugget coeffi cient is the ratio of the nugget value to the sill value. If the ratio is less than 25%, the system has a strong spatial correlation, if between 25 and 75%, the system has moderate spatial correlation. If the ratio is more than 75%, the spatial correlation of the system is very weak (Yang et al. 2009). The size of the fractal dimension D represents the curvature of the semi-variogram curve, and the comparison between the D values of different variables can determine the degree of spatial heterogeneity (Wang et al. 2000).

For the regionalized variable fuel moisture content, the semivariogram γ( h) is not only related to the interval distance h, but also to the direction (Webster 1985). When a variogram is constructed in a particular direction, it is called an anisotropic variogram expressed as γ( h, θ), and γ( h) is called isotropic variogram (Li et al. 1998). The anisotropy ratio f K( h) describes the anisotropic structure of the moisture content. If K( h) is equal to or close to 1, the spatial heterogeneity is isotropic, otherwise it is anisotropic (Li et al. 1998).

The anisotropic equation is:

where γ( h, θ1) is the semi-variogram in θ1direction; γ( h, θ2) is the semi-variogram in θ2direction.

Error statistics of fuel moisture content data by different sampling methods

The moisture content measured by sampling is used for simulated sampling analysis. There are controlled, uncontrolled, and random sampling methods (Mao et al. 2012).

In the simulated controlled sampling, the moisture content data was sampled at intervals of h = 1, 2, …, 4 m; sampling intensity is the number of sampling points, indicated by m, m = 1, 2, …, 20, αh,mis the standard error when sampling intensity is m and the sampling interval is h. The equation is:

where xiis the sample moisture content at i;̄x is the average sample moisture content; n is the number of samples.

In the simulated uncontrolled sampling, the smaller the sampling interval, the more samples that can be taken. The moisture content error is calculated by the maximum value of the sampling intensity m; the maximum value of m is n/ h. In the simulated random sampling, m samples are randomly taken from the moisture content data ofeach layer in each direction, m = 1, 2, …, 24, to calculate the average standard error.

Results and analysis

Statistical description of moisture content of fuel material

The average moisture content in each layer was: litter layer < semi-humus layer < humus layer, and the water content of the H litter layer was the lowest (11.3%). From the coefficient of variation, the variability of the moisture content in the litter layer was highest in all directions (4.2–8.8%), in the semi-humus layer moderate in all directions (4.3–6.0%), and in humus layer lowest in all directions (3.3–4.6%) (Table 1).

Geostatistics spatial on heterogeneity of fuel moisture content

The three H layers and O litter layer are linear models; the V litter layer, V semi-humus layer and O humus layer are exponential models; the O semi-humus layer is a Gauss model; and, the V humus layer is a spherical model. Figure 4 is a variation function model curve of the moisture content. According to the fitting model, the minimum coeffi cient of the V litter layer is 0.0350, the minimum coeffi cient of the H semi-humus layer is 0.0190, and the minimum coeffi cient of the O humus layer is 0.0520.

According to the parameters from the semivariogram fitting model, the sill value of the litter layer in three directions from high to low is V (0.0155) > H (0.0120) > O (0.0067); the sill value of the semi-humus layer from high to low is O (0.1592) > V (0.0736) > H (0.0497); and, the sill value of the humus layer from high to low is V (0.0753) > O (0.0532) > H (0.0276). The variation ranges of the V litter layer, V humus layer and O humus layer is from 3.5 to 5.5 m, indicating aspatial correlation of fuel moisture content at this distance (Table 2).

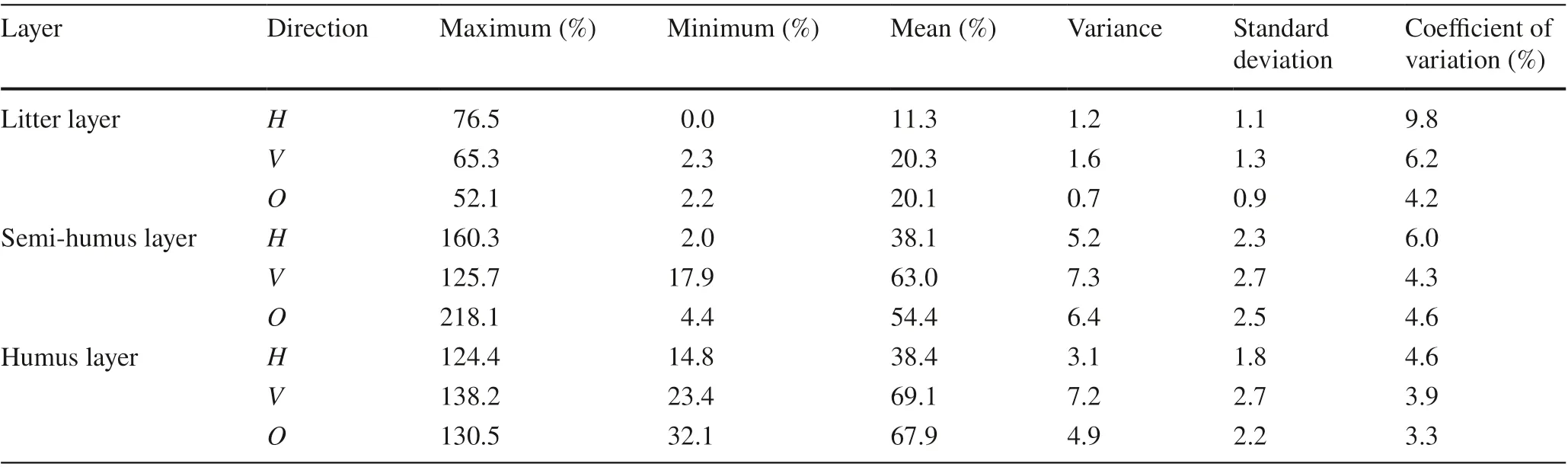
Table 1 Dead fuel moisture content in a Larix gmelinii forest

Fig.4 Semivariogram model curve of fuel moisture content

For the high or higher spatial correlations, there are O semi-humus layer, O litter layer and V three layers, and the lowest nugget coeffi cient is 0.0968. The fractal dimension of fuel moisture content in three directions is higher, ranging from 1.8640 to 1.9930 and the highest fractal dimension is the V litter layer, which is 1.9930. The lowest fractal dimension is the O semi-humus layer, which is 1.8640. The difference of the fractal dimension ofeach moisture content is relatively small, but the degree of spatial heterogeneity caused by spatial correlation can still be seen.

Anisotropy of the fuel moisture content

Samples were taken in three directions and the data were subject to anisotropic analysis and compared. K( h) values deviated from 1 (Fig.5). According to the anisotropy curveof litter layers, the variation of O was less than that of H and V. Comparing the variation of H and V anisotropy, the variation of H was greater than that of V in the range of 34–47 m, otherwise the variation of V was greater than that of H, indicating the complexity of variation of surface fuel moisture content in both directions. The anisotropy of the semi-humus layer is complex or there is no anisotropy; in comparing the variation of V and O, the anisotropy ratio ranged from 0.55 to 1.55, indicating a more changeable trend; the anisotropy curves of the humus layer showed strong spatial anisotropy, and the anisotropy comparison result was V > O > H. This shows that the anisotropy of the moisture content of the semi-humus layer in this Larix gmelinii forest was insignificant or changeable.

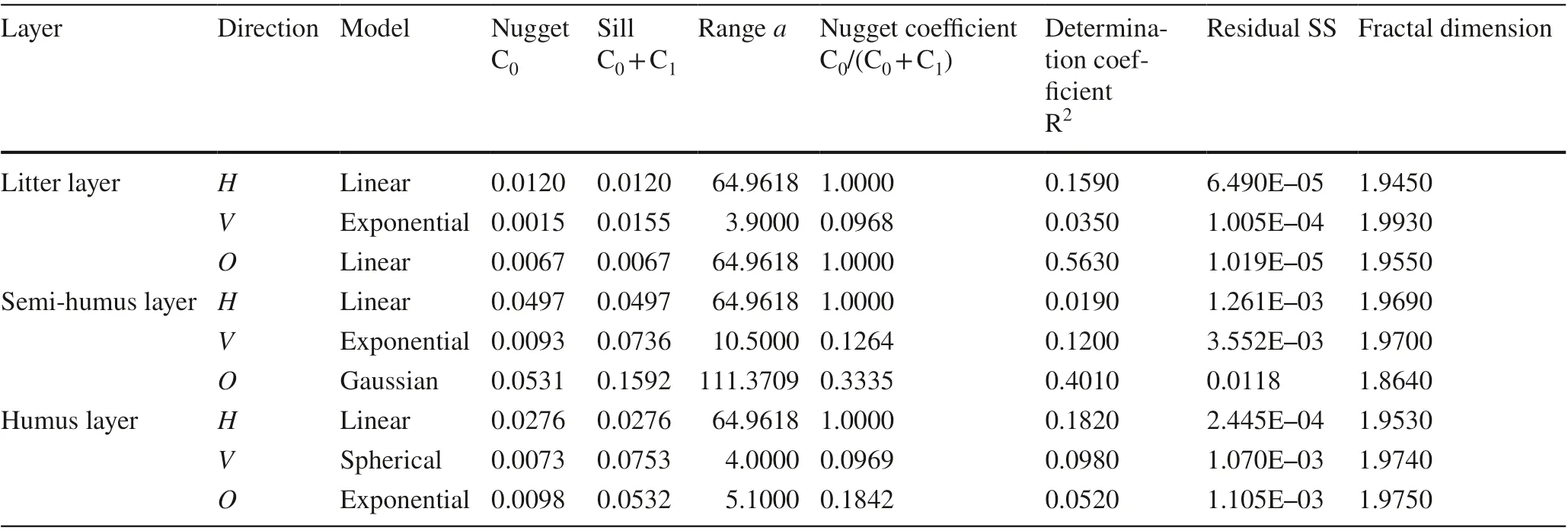
Table 2 Semivariogram model and related parameters of fuel moisture content in a Larix gmelinii forest

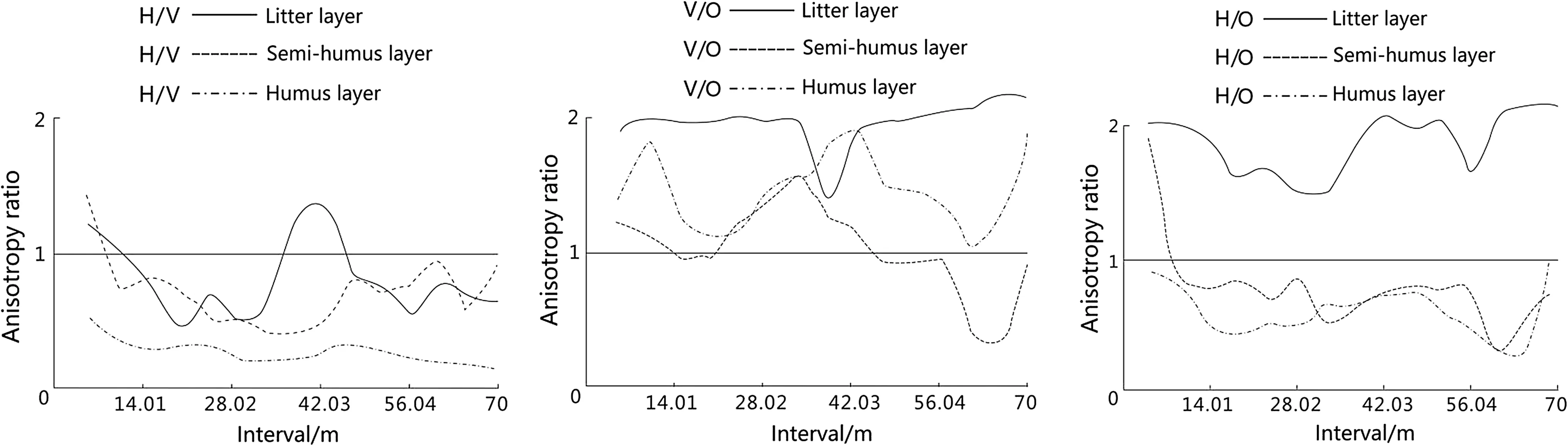
Fig.5 Anisotropy ratio curve of dead fuel moisture content in three transects

Error analysis of the estimation of the fuel moisture content

The analysis of simulated sampling data shows that the sampling error will increase with an increase of sampling interval in uncontrolled sampling (Fig.6). Therefore, reducing the sampling interval and increasing sampling intensity as much as possible can reduce the error but it has little practical significance.

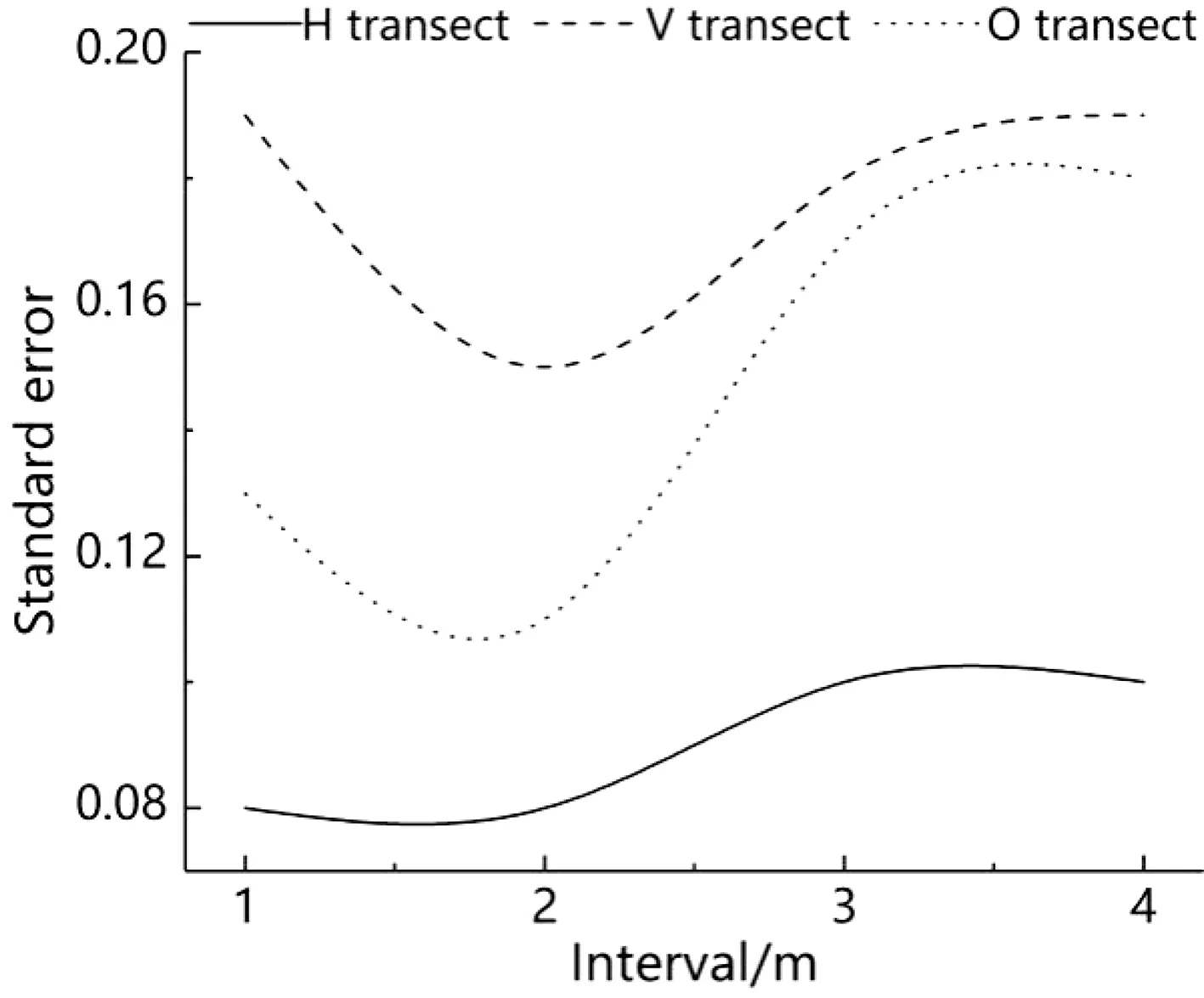
Fig.6 Simulated uncontrolled sampling error analysis

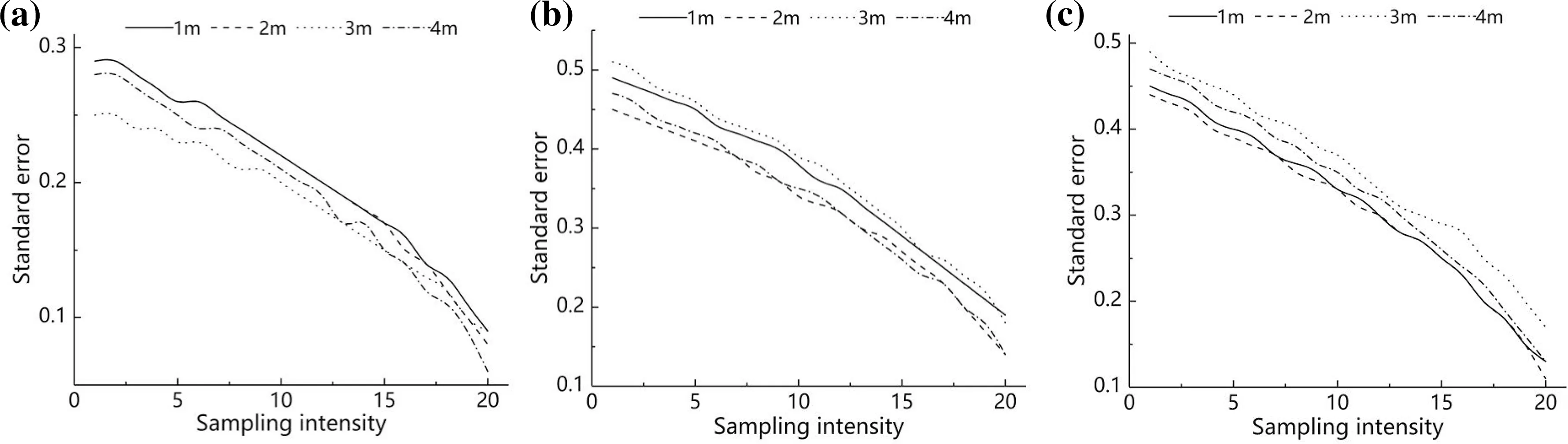
Fig.7 Simulated controlled sampling oferror analysis in a H direction, b V direction, and c O direction

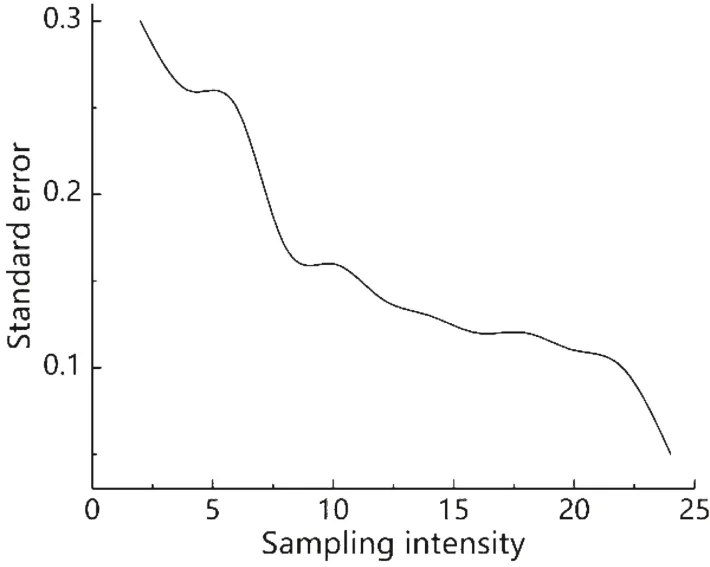
Fig.8 Random sampling simulation error analysis

The results of simulated controlled sampling (Fig.7) can be observed from the error analysis in H, V, O directions: when the sampling interval is 1‒4 m, the error decreases but not obviously with an increase of sampling interval; when the sampling intensity in three directions increases, the standard error decreases finally to 0.1. In the H direction, when the sampling interval is 3-m and the sampling intensity 16, the standard error is reduced to 14.1%; in the V direction, when the interval is 4-m and sampling intensity 20, the standard error is 13.9%; in the O direction, when the interval is 2-m and the intensity 19, the standard error is 14.6%.

Error analysis of simulated random sampling shows that the standard error decreases with the increase of sampling intensity (Fig.8). Within the sampling intensity, m = 1, 2, 3, …, 24, more than eight samples are required to keep the standard error below 15%. Due to the randomness of the sampling interval and the large range oferror variation during random sampling, the results are not representative.

Discussion

Effects of general statistics and geostatistics on spatial heterogeneity of fuel moisture content

Different statistical methods were used to study spatial heterogeneity of the dead fuel moisture content. The average water content in the litter layer, semi-humus layer and humus layer was 17.2%, 51.8%, and 58.4%, respectively. The closer to the surface, the lower the water content of the fuel. This is consistent with Man et al. ( 2019) on the dynamic moisture content changes of three layers surface fuel. The moisture content of the surface fuel is most related to climatic factors of the day or the previous day. These have a significant impact on the moisture content of the litter layer, then on the semi-humus. The surface litter layer has the lowest water content, possibly because the litter layer fuel has more and larger pores and water permeability is strong, promoting downward infiltration. In field sampling, as sampling depth and fuel moisture content increase, the coeffi cient of variation decreases, which is similar for soil moisture in the Taiyueshan small watershed in Shanxi (Wang et al. 2017) and for soil water content (Owe et al. 1982). This indicates that moisture content in the litter layer is more affected by external conditions than lower layers (Yin et al. 2013), and that the spatial distribution of the fuel moisture content in the lower layers is relatively homogeneous and stable, while the spatial variation of the moisture content in the litter layer is more active (Qiu et al. 2016). In terms of directional variation, the coeffi cient of variation of H and V moisture content is largest in the litter layer, indicating that the variation of fuel moisture content in litter layer is the largest in these two directions, while in the O direction, the coeffi cient of variation was largest in the semi-humus layer is the largest, which indicates that the variation of fuel moisture content in semi-humus layer is the largest in this direction. The standard deviation of fuel moisture content of three layers in three directions is the largest in the V direction, indicating that the data are more discrete and that there are significant differences among different sampling points. These statistical results may be related to soil structure, vegetation status, sampling method, and climate factors.

This study used the principles and methods of geostatistics, combined with ground survey data, to visually describe the spatial distribution of dead fuel moisture content (Liu et al. 2008). Mao et al. ( 2012) investigated the spatial heterogeneity of surface fuel moisture content in a Larix gmelinii forest and reported that the maximum sill value of the litter layer in the O direction was the highest (0.1632), followed by the value in the V direction, and the value in the H direction was the smallest. The humus layer of the H direction was the largest (0.1276). Generally, the spatial heterogeneity of the litter layer is higher than that of the humus layer (Mao et al. 2012). In this study, the order of sill value of the litter layer was V > H > O, the semi-humus layer O > V > H, and the humus V > O > H. Overall, the spatial heterogeneity of the moisture content of the semi-humus layer was the highest, that of the humus layer moderate, and lowest in the litter layer. It can be seen that the total spatial heterogeneity of fuel moisture content at different depths was different.

Effects of sampling methods on fuel moisture content

The spatial heterogeneity of fuel moisture content is closely related to factors of sampling methods and to natural processes. In estimating the total moisture content of the sampling area by stimulated sampling reasonable control of the sampling interval, and increasing sampling intensity can reduce error. When the sampling intensity is increased to more than 16 times and the sampling interval is 3 m, the standard error is < 15%. At the same sampling interval, with an increase in the number of sampling points, the rate oferror reduction is increased (Yan et al. 2019). Zhang et al. ( 2017) studied the spatial heterogeneity of soil moisture in the slope land reconstruction and natural grassland reconstruction in degraded red soil area and concluded that increasing sampling density and scale could better reveal the spatial heterogeneity of soil moisture. Xing et al. ( 2015) considered that increasing the sampling points could improve the accuracy of soil moisture monitoring. These are consistent with the results of this study.

Compared with Mao et al. ( 2012) on the spatial heterogeneity of fuel moisture content, the results in this study may better reflect the spatial heterogeneity of fuel moisture content. This may be because the selected samples were taken in three layers and the sampling intensity was greater, the results were more representative. The optimal sampling intensity depends on sampling interval, the degree of variation and the variation rate of the indicators (Conen et al. 2005). By controlling the sampling interval, sampling intensity can be appropriately reduced within a certain interval limit, thereby obtaining a more accurate estimate of fuel moisture content.

Conclusion

The spatial heterogeneity of the dead fuel moisture content in the litter, semi-humus and humus layers in three directions, vertical, horizontal and slant in a Larix gmelinii forest was analyzed using geostatistics. The spatial heterogeneity of fuel moisture content was highest in the semi-humus layer. This has practical bearing for a statistical study of dead fuel moisture content and lays the basis for the prediction of the spread rate of a surface fire to underground fire when forest fires occur. In addition, it has a role in predicting the fire risk level and the forest burned area to provide a basis for the development of firefighting plans.

In this study, only the dead fuel in a sample area in a L. gmelinii forest was selected and only during the autumn fire prevention period, and the selected plot was on a sunny slope. Therefore, in future research, it will be necessary to establish multiple experimental plots in different fire seasons and on different slope directions and positions. This will improve the accuracy of moisture content measurement, reduce experimental errors, increase the accuracy of fire risk prediction and provide a theoretical basis for effective prevention and control of forest fires.

AcknowledgementsData measurement and analysis were provided by the Saihanwula Forestry Ecosystem Positioning Research Station in Inner Mongolia.

References

Bi HX, Li XY, Liu X, Li J, Guo MX (2006) Spatial heterogeneity of soil moisture using geological statistics method in the loess region of west Shanxi Province. J Beijing Forest Univ 28(5):59–66 (in Chinese)

Conen F, Zerva A, Arrouays D, Jolivet C, Jarvis PG, Grace J, Mencuccini M (2005) The carbon balance of forest soils: detectability of changes in soil carbon stocks in temperate and boreal forests. SEB Exp Biol Ser 2005:235–249

Ettema CH, Wardle DA (2002) Spatial soil ecology. Trends Ecol Evol 17(4):177–183

Fu TG, Chen HS, Zhang W, Gao P, Wang KL (2014) Spatial variability of soil moisture content and its influencing factors in small Karst catchment during dry period, China. Trans Chin Soc Agric Eng 30(14):124–131 (in Chinese)

Han YZ, Wang ZQ (2002) Spatial heterogeneity and forest regeneration. Chin J Appl Ecol 5:615–619 (in Chinese)

Hao JX (2005) The study on spatial heterogeneity of soil water and salinity in oasis and transition between oasis and desert of Zhangye City. Doctoral dissertation. Northwest Normal University (in Chinese)

Hernandez-Stefanoni JL, Ponce-Hernandez R (2006) Mapping the spatial variability of plant diversity in a tropical forest: comparison of spatial interpolation methods. Environ Monit Assess 117(1–3):307–334

Ivanov VY, Fatichi S, Jenerette GD, Espeleta JF, Troch PA, Huxman TE (2010) Hysteresis of soil moisture spatial heterogeneity and the “homogenizing” effect of vegetation. Water Resour Res. https ://doi.org/10.1029/2009W R0086 11

Jing S, Tian J, Wang JY, Wang QF, Yang GD, Guo DL, Yu GR (2016) Small-scale spatial heterogeneity of soil organic matter fractions within an original broad-leaved Korean pine forest in Changbai Mountain. Acta Ecol Sin 36(20):6445–6456 (in Chinese)

Li HB, Wang ZQ, Wang QC (1998) Theory and methodology of spatial heterogeneity quantification. Chin J Appl Ecol 6:93–99 (in Chinese)

Li M, Duan WB, Chen LX, Wei L, Feng J, Wang SQ (2012) Geostatistical analysis on spatiotemporal distribution pattern of soil water content of forest gap in Pinus koraiensis dominated broadleaved mixed forest. Acta Ecol Sin 32(5):1396–1402 (in Chinese)

Li YD, Cui X, Wen P, Yan JX (2015) Research progress on water content of forest fuel. For Fire Prevent 4:39–41 (in Chinese)

Liu L (2013) Patial variability of soil organic carbon and nutrients in typical forestlands in low mountain area of Changbai Mountain. Beijing Forestry University, Beijing (in Chinese)

Liu BX, Shao MA (2012) Soil water content heterogeneity at smallscale on degraded grasslands on Loess Plateau. Sci Soil Water Conserv 10(4):60–65 (in Chinese)

Liu ZH, Chang Y, Chen HW, Zhou R, Jing GZ, Zhang HX, Zhang CM (2008) Spatial pattern of land surface dead combustible fuel load in Huzhong forest area in Great Xing’an Mountains. Chin J Appl Ecol 19(3):487–493 (in Chinese)

Man ZY, Hu HQ, Zhang YL, Liu FC, Li Y (2019) Dynamic change and prediction model of moisture content of surface fuel in Maoer Mountain of northeastern. J Beijing For Univ 41(3):49–57 (in Chinese)

Mao WX, Tong DH, Zhang C, Zhao DD, Ding YY, Jin S (2012) Spatial heterogeneity of moisture content of land surface dead fuel in larch stand and effects of sampling methods on moisture estimation. J Northeast For Univ 40(5):29–33 (in Chinese)

Matheron G (1963) Principles of geostatistics. Econ Geol 58(8):1246–1266

Owe M, Jones EB, Schmugge TJ (1982) Soil moisture variation patterns observed in Hand County, South Dakota. J Am Water Resour Assoc 18(6):949–954

Qiu BG, Li YX, Yang XL, Ma HP (2016) Distribution pattern of soil moisture spacetime of forestland in semi-arid valley of Lhasa, southwestern. J Beijing For Univ 38(11):9–15 (in Chinese)

Shi LL (2012) Study on the spatial heterogeneity of soil physical and chemical properties of primary tropical montane rainforest in Jianfengling. Chinese Academy of Forestry, Hainan Island (in Chinese)

Song D, Li H, Liu SJ, Zou GY, Liu DS (2019) A geostatistic investigation of the comprehensive evaluation of fertility and spatial heterogeneity of forest soil nutrients in hilly and mountainous regions of southern China. Arab J Geosci 12(9):292

Wang J, Fu BJ, Qiu Y, Chen LD (2000) Spatiotemporal variability of soil moisture in small catchment on Loess Plateau—semivariograms. Acta Geogr Sin 4:428–438 (in Chinese)

Wang J, Fu BJ, Qiu Y, Chen LD, Wang Z (2001) Geostatistical analysis of soil moisture variability on Da Nangou catchment of the loess plateau. China Environ Geol 41(1–2):113–120

Wang QH, Yu XS, Li SY, Tong YM, Liu B, Ruan DZ (2012) Study on dynamic characteristics of forest fuel. For Invent Plan 37(5):40–43 (in Chinese)

Wang T, Kang FF, Han HR, Cheng XQ, Bai YC, Ma JY, Guo ZH (2017) Factors influencing spatial heterogeneity of soil moisture content in a small catchment of Mount Taiyue, Shanxi Province. Acta Ecol Sin 37(11):3902–3911 (in Chinese)

Webster R (1985) Quantitative spatial analysis of soil in the field. Adv Soil Sci 3:61–70

Xing XG, Zhao WG, Liu Y, Ma XY (2015) Spatial variability of soil moisture in kiwi field under different sampling density conditions. Trans Chin Soc Agric Mach 46(8):138–145 (in Chinese)

Yan BL, Zhao QG, Zhang B, Li YL, Zhao PW, Zhang H (2017) Effects of different vegetation types on soil physicochemical properties and soil respiration. Ecol Environ Sci 26(2):189–195 (in Chinese)

Yan JX, Sun Q, Li JJ, Li HJ (2019) Effect of the sampling scale and number on the heterogeneity of soil respiration in a mixed broadleaf-conifer forest. Environ Sci 40(1):383–391 (in Chinese)

Yang YJ, Zhu JH, Liu SH, Tang Y, Liu YZ, Feng WJ (2009) Spatial statistic properties of agronomic parameters and soil moisture content in wheat jointing stage. Trans Chin Soc Agric Mach 40(S1):159–164 (in Chinese)

Yin H, Li H, Jiang ZC, Yang QY, Wang Y (2013) Spatial heterogeneity of soil moisture in typical karst areas. Jiangsu Agric Sci 41(7):332–336 (in Chinese)

Zhang XG (2016) Spatial distribution of soil moisture in southern slope of Qilian Mountains. Qinghai Normal University, Xining (in Chinese)

Zhang SL, Yong WY, Yang YX, Lu ZX, Zhang F, Li GL (2008) Study on the vegetation classification in Saihanwula mature reserve. J Inner Mongolia Univ 01:74–79 (in Chinese)

Zhang HW, Ma JY, Zhang ZW, Sun T, Lv GH (2009) Utilization of and research on geostatistics in soil science. J Lanzhou Univ (Nat Sci) 45(6):14–20 (in Chinese)

Zhang ZJ, Liu LY, Liu YQ, Wu CS, Qiu MY, Guo JR, Deng WP (2017) Spatiotemporal variation of soil moisture in summer season during process of vegetation restoration in degraded red soil region. J Southwest For Univ 37(3):88–94 (in Chinese)

Zhang H, Dong CC, Niu S, Zhang YL, Jin S, Wang YX (2018) Effects of different sampling methods on forecast model accuracy of predicting fuels in forests in Pangu forest farm, China. J Cent South Univ For Technol 38(5):33–39 (in Chinese)