多任务学习正则化模型对患者的分类研究

（长安大学，陕西 西安 710000）

0 引 言

神经成像技术已成为大脑结构和功能研究的重要工具，这一技术也被应用于研究精神分裂症患者（SZ）的脑结构和功能。遗传因素在精神分裂症患者的大脑发育中具有重要作用。结合神经影像学和遗传学研究技术，可以探索和评价与脑相关基因多态性对脑功能的影响，了解这些基因对精神分裂症行为的影响。

近年来，精神分裂症的组学研究也在不断发展，包括基因组学、表观基因组学、转录组学、蛋白质组学和代谢组学。然而，精神分裂症的病因是由多种因素引起的，且多种因素之间相互作用[1-2]。单一组学研究只能对造成紊乱的因素提供部分解释，而多组学数据的整合适合多种因素的研究。事实上，已有相当多的研究致力于通过多组数据集成来研究各种疾病。之前的工作主要集中在一种成像模式上（如静止状态或任务fMRI）。在神经影像学研究中，通常从相同的实验对象中获取多模态影像以提供补充信息。最近，人们在多任务学习框架中引入了多种模式以预测大脑认知分数，并对SZ和阿尔茨海默病（AD）的诊断进行分类[3-5]。

受文献[6]方法的启发，本文使用随机森林策略计算模型中样本之间的相似度，通过联合学习少量的共同特征，吸收来自多种模式的互补信息；采用新的流形正则化器来保存模内和模间数据的结构信息。从机器学习的角度看，正则化项可以提取更多的判别特征，从而提高后续预测的性能。本文利用该算法结合单核苷酸多态性（SNP）、DNA甲基化和功能磁共振成像（fMRI）三种不同类型的数据，对SZ进行分类任务，展示模拟数据和真实数据分析（fMRI，SNP和Methylation）的实验结果，并与其他现有模型进行比较，所设计分类方法的分类精度为86.07%。结果表明，在均方根误差和相关系数的度量下，我们提出的模型与其他竞争模型相比，性能得到了改善。

1 模型的算法设计

多任务学习（MTL）的目的是通过利用多个任务之间的关系来提高其性能，特别是当这些任务具有一些相关性或共时性[7]。本文提出了一种多重正则化的多任务学习模型，用于从多个模式中联合选择少量的共同特征，并在分类中取得优异的性能，其中每个模式都被视为一个任务。重要的是，与经典的多任务学习模型相比，该模型加入多个正则化器，考虑了各模态内数据的结构信息。

1.1 经典多任务学习模型

假定给出M个学习任务（M组模态数据），我们表示第m个模态为：

式中：M=1, 2,...,m；代表了第i个样本在第m个模态下的特征向量；d和N分别表示特征的个数和样本数量。令y∈RN为样本数据的响应向量，w(m)∈Rd为第m个模态的回归系数向量。式（2）给出了经典多任务学习模型求解优化问题：

1.2 多任务学习正则化模型

经典的MTL模型只考虑了数据与响应值之间的关系，忽略了数据的结构信息，很可能导致较大的偏差。为了使相似的样本具有相似的响应值，可以通过计算样本之间的距离并转换到相似性度量来依次描述样本之间的相似程度。使用权值和大小为N×N邻接矩阵L来表示样本之间的相似度，其中，L(m)(a,b)用于表示样本a与样本b在第m个模态下的相似度。相似度矩阵L可以用不同的方法计算，常用的方法为利用欧几里得距离计算一对样本之间的距离，并对其进行规格化，形成相似度矩阵。随机森林可以提取多种形式的相似性度量对，通过提供一致的方式组合不同类型的特征数据。基于样本相似度矩阵，定义样本相似度正则化如式（3）所示：

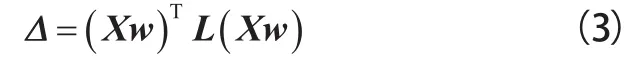
我们希望将数据的全局结构信息保存在原始特征空间中，并使用随机森林生成的相似度矩阵来表示。在每个模态中构造一个相似矩阵来表示数据的远近关系结构。可以定义基于样本相似性的多模态特征选择目标函数，如式（4）所示：

在上述模型中，使用多任务的多组数据关联分析，不仅可以共同选择不同类型数据中的共享信息，也可保持相似性信息渐变样本在每个任务中的样本相似性。现有的多模式特征选择算法仅考虑成对样本之间的关系或只考虑信息之间的几个点样本的邻域，只使用局部信息而忽略了样本集之间的全局相似性关系[9]。

2 模型的优化与求解

由于目标函数不可微且不光滑，没有办法计算某些点的梯度，所以目标函数不能直接采用梯度下降法求解。在此类问题上有很多方法可以求解目标函数式（4），如交替方向乘数法（ADMM）[10]和加速近端梯度法（APG）[11]。本文使用APG算法解决上述目标函数的优化求解问题。

首先，将目标函数划分为两部分，即f(w)+g(w)，分别如公式（5）和公式（6）所示：

式中，f(w)为凸可微，g(w)为凸不可微。迭代更新w，并用公式（7）近似f(w)+g(w)：

式中：表示矩阵X1TX2的迹；||·||F表示弗罗贝尼乌斯范数（Frobenius norm，F-范数）；Δf(w(t))表示f(w)在第t次迭代时在w(t)处的梯度；l表示迭代的步长。由APG算法可以得到关于系数权重矩阵w的迭代公式：

训练得到权重矩阵w，之后得到计算结果的响应值，将其中每个元素与阈值0进行比较，如果测试响应值大于0，则样本i的标号预测为+1；否则，预测为-1。分别在各测试子集上验证，最后计算分类精度。

3 实验结果与分析

3.1 模拟数据的测试

在真实集测试之前，本文在仿真数据集上对算法进行了验证。首先按照双螺旋模式生成单视图数据集。每个数据集包含200个具有二元表型和二维测量的受试者。在模拟数据集中，每个螺旋的度数设置为540°，噪声水平逐渐提高，使得缠绕的螺旋更加接近。将数据集导入本文算法中，同时将数据集导入具有径向基核函数（RBF）的SVM中进行比较。

首先使用80%～90%的整体数据作为训练数据来测试分类性能。当噪声等级K≤1时，该模型和SVM的分类准确率均超95%；当K≤3时，两者的分类准确率均超90%。针对这些情况，两种算法的分类准确率无显著差异（p值<0.05）。基于有限标记训练数据的分类精度，本文的多任务学习正则化模型在所有噪声水平上都优于SVM。随着噪声水平的提高，该模型与SVM的分类准确率均下降。

模拟数据实验结果表明，多任务学习正则化模型的鲁棒性优于SVM，在分类性能上效果较好，实验结果如图1和图2所示，分别展示了SVM随噪声等级提高的误差率和多任务学习正则化模型随噪声等级提高的误差率。

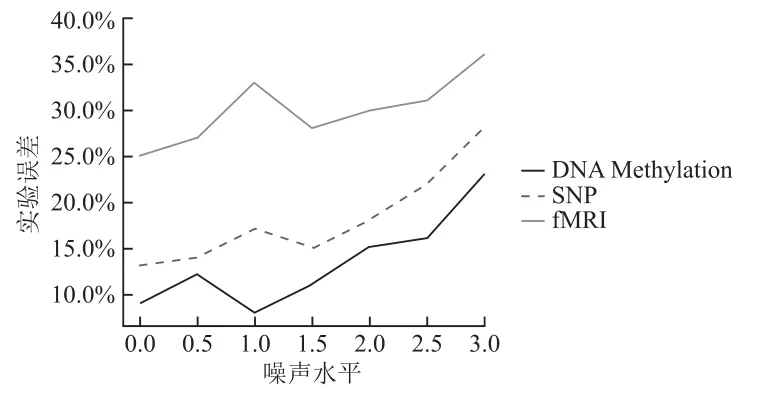
图1 SVM在仿真数据上的误差

图2 多任务学习正则化在仿真数据上的误差

3.2 真实数据的测试

本文采用数据集大小为SNP：184×722 177，fMRI：184×41 236，DNA甲基化：184×27 508。首先使用随机森林策略分别计算3组数据样本之间的相似度，通过十折交叉验证（CV）技术评估模型的分类性能。即首先将整组被试集随机分为10个大小相近的不相交子集，然后依次选取每个子集作为测试集，其余9个子集用于训练预测模型，利用训练后的模型对测试集中的受试者进行分类，重复10次，以减少CV中抽样偏差的影响。最后，分类精度达到86.07%。所有正则化参数模型的正则化参数γ和λ在训练集上通过网格搜索各自范围，即γ，λ∈{0.001，0.003，0.01，0.03，0.1，0.3，1，3，10}。

将多任务学习正则化模型与其他分类方法进行比较，结果如图3所示。

图3 多种方法的分类精度比较

测试的其他分类方法包括基于单个组学数据图、多数邻域平均融合（MMN）[12]、基于相似网络融合的支持向量机（SSVM）[13]。在分类精度方面，本文提出的模型对SZ的分类精度高于其他集成方法。此外，与任何单一组学数据进行分类方法对比，将三种类型的数据与优化权重集成多任务学习正则化模型具有更高的准确性，这进一步验证了该模型在数据集成方面的优越性。

4 结 语

本研究的重点是多任务学习正则化算法，利用随机森林的策略度量样本之间的相似性，如果用其他方法构造相似矩阵，分类性能会发生变化。例如，子空间聚类也可用于构建高维数据的相似矩阵[14-15]。相似度度量方法的选择取决于数据集，特别是在先验特征选择方面[16-17]。除使用组稀疏正则化联合选择多个模态（任务）一组小的共同特征外，还设计了新的流形正则化以保存模态内部和模态之间的结构信息，此举提高了后续分类的准确性，实现了对精神分裂症患者分类的目的，为现代医学区分慢性疾病提供了有效的解决思路。本文在模拟数据和真实数据上分别进行了测试，证明了该模型具有较强的鲁棒性，并在真实数据分类的分类精度上达到了86.07%，与其他算法相比具有明显优势。