关于Smarandache LCM函数的方程的可解性

姜莲霞，傅 湧

*姜莲霞1，傅 湧2

(1.喀什大学数学与统计学院，新疆，喀什 844008；2. 宜春学院数学与计算机科学学院江西，宜春 336000)

令()为Smarandache函数，()为Smarandache LCM函数，2()为广义欧拉函数。讨论方程((14))=2()和((36))=2()可解性，利用初等方法并结合函数2()与函数()的性质，给出了这两个方程的所有正整数解。

广义欧拉函数；Smarandache函数；Smarandache LCM函数；正整数解

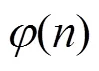
1 相关引理

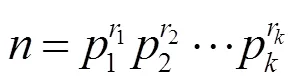
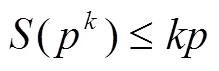
2 定理及其证明

定理1方程

又因

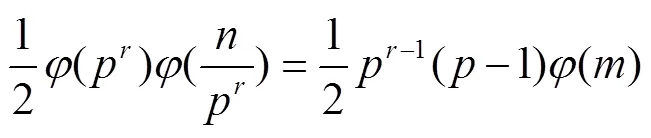
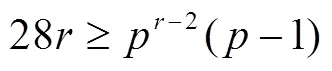
定理2方程

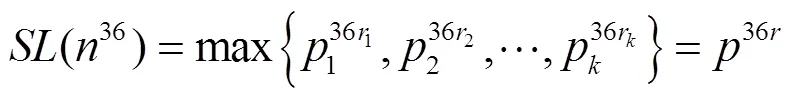
又因

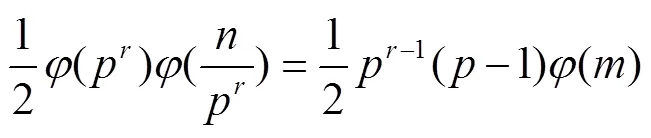
综上所述，可得方程（5）的正整数解为=15987，21316，31974，1920。定理2证毕。

[1] Smarandache F. Only Problems ,Not Solutions[M]. Chicago: Xiquan Publishing House,1992．

[2] Sandor J.On a dual of the Pseudo Smarandache Function[J].Smarandache Notion Journal,2002,13:18-23.

[3] Richard P.Some properties of the Psedo Smarandache function[J].Scientia Magna,2005,1(2): 167- 172．

[4] Kenneth Ireland,Michael Rosen.A classical introduction to Modern Number Theory[M]．New York:Springer- Verlag，1990.

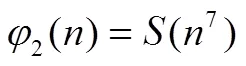
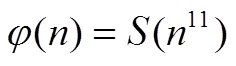
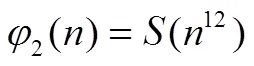
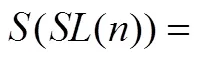
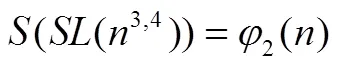
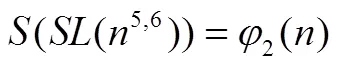
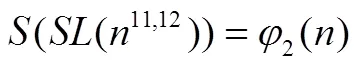
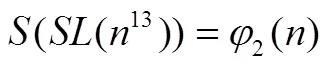
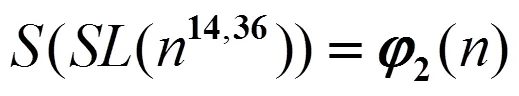
*JIANG Lian-xia1, FU Yong2

(1. College of Mathematics and Statistics, Kashi University, Kashi, Xinjang 844006, China; 2. School of Mathematical and Computer Science, Yichun University, Yichun, Jiangxi 336000, China)

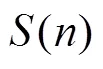
Generalized Euler function; Smarandache function; Smarandache LCM function; positive integer solutions

O156

A

10.3969/j.issn.1674-8085.2021.02.001

1674-8085(2021)02-0001-06

2020-10-20；

2020-11-23

喀什大学校内一般课题项目（(19)2652）

*姜莲霞(1987-)，女，河南驻马店人，讲师，硕士，主要从事代数与数论研究(E-mail:1210981614@qq.com);

傅湧(1963-)，男，江西新干人，副教授，主要从事非线性泛函分析研究(E-mail:1010064326@qq.com).