海洋可控源三维电磁响应显式灵敏度矩阵的快速算法*

陈博 汪宏年† 杨守文 殷长春

1) (吉林大学物理学院， 计算方法与软件国际中心， 长春 130012)

2) (吉林大学地球探测科学与技术学院， 长春 130026)

1 引 言

海洋可控源电磁测量(marine controlled-source electromagnetic measurement， MCSEM)主要应用于海底构造勘探、油水特征识别和海上油气储层定量评价， 以便于降低海上盲钻率和勘探成本.其典型测量方式是用随船拖曳移动的低频(0.1—10 Hz)水平电偶极子发射天线， 通过布设在海底的接收机测量电磁场强度， 并根据多频、多源距接收信号变化特征判断地下电导率空间分布情况[1，2].由于海底地形构造复杂以及地层横向电阻率分布不均匀， 在海洋可控源电磁采集方案设计以及海洋电磁资料处理和解释过程中， 往往需要进行大量的数值模拟、灵敏度计算以及反演成像等工作.因此，近几十年来， 围绕着海洋可控源电磁响应的正演模拟、灵敏度矩阵计算以及反演成像技术均得到快速发展[3，4].

在正演模拟方面， 各种解析和数值方法在海洋可控源电磁理论中均得到广泛研究与应用， 例如一维水平层状地层中的解析法[5-8]、三维有限元法[9，10]、三维有限体积法[11-14]、三维积分方程法[15]以及2.5 维混合法[16]等.在反演成像方面， 主要以高斯-牛顿算法或共轭梯度算法等迭代反演算法为主， 原理是通过逐步修改地层电导率参数实现理论合成数据与实际输入资料的最佳拟合， 其中包括:一维Occam 反演[17]和一维多参数迭代反演[18-21];以积分方程为基础的二维、三维迭代反演[22]以及以有限体积法或有限元法为基础的二维、三维反演成像[23-27]和参数化反演技术[28-30]等.

在整个反演成像中均涉及到电磁响应显式灵敏度的计算， 以便确定目标函数下降方向.通过研究不同接收、不同收发距电磁场灵敏度矩阵的变化特征， 也能够为接收点位置以及收发距优化提供理论依据， 并有助于提高数据采集效率以及减少反演工作量等.因此， 如何快速有效地计算海洋可控源电磁响应的显式灵敏度已发展成为一个专门的研究问题[31，32].在电磁反演成像的所有算法中， 除了一维层状地层和含井眼的轴对称电导率地层中的Fréchet 导数可以通过电磁场解析解[17-22]或半解析解[29，30]进行有效计算外， 在其他的二维和三维电磁反演技术中， 电磁响应的Fréchet 导数只能够通过数值方法近似计算.目前主要有两种不同的计算路线: 直接法和伴随法[31].伴随法主要利用电磁场伴随方程的Green 函数与一阶Born 近似， 将电导率摄动产生的电磁场变化表示成体积分的形式，从而得到电磁场微小变化与电导率摄动量间的线性关系[32-34].在二维和三维反演问题中， 由于伴随方程的Green 函数通常没有解析解， 需要通过数值计算技术确定各个接收点上的伴随Green 函数，当接收点很多时会大大增加Fréchet 导数的计算工作量.直接法则是通过各种数值方法求解摄动方程， 建立相应的电磁场微小变化与电导率摄动量间的关系， 目前应用最多的方法是对电场离散方程=S 进行摄动处理， 并通过迭代法求解摄动方程确定电磁响应的Fréchet 导数[23，24，32]， 显然随着摄动电导率单元数量的不断增加， 灵敏度矩阵计算的工作量也会线性增加.为了提高三维电磁反演效率， 利用地层电导率空间分布特点， 可以分别采用像素反演或参数化反演两种不同方法[28，35]， 因而迫切需要为像素反演或参数化反演建立一套统一高效的灵敏度矩阵计算技术.

本文将借助电场耦合势Helmholtz 方程的三维有限体积法， 结合直接法求解技术与严格的偏微分方程摄动理论， 为海洋可控源电磁三维像素反演或参数化反演问题研究建立一套显式灵敏度矩阵的准确高效算法.首先， 利用Yee 氏交错网格节点和有限体积法对电场耦合势Helmholtz 方程进行离散[10，11]， 建立移动源耦合势离散方程， 并将直接法求解器与三维线性插值技术结合， 给出同时计算多移动电磁场的一种新算法.在此基础上， 进一步针对像素电导率模型(假定电导率空间连续变化)和分块常数电导率模型(参数化模型)， 将电导率函数和其摄动量表示成Yee 剖分网格 Vi，j，k上分片块状函数组合形式， 借助一阶Born 近似与多移动源电场耦合势正演结果， 将电导率摄动产生的一次空间散射电流定量表示为各个剖分单元上散射电流的叠加， 再利用有限体积法对所有散射电流进行离散处理， 得到表征电导率摄动量与耦合势微小变化之间关系的大型离散方程组.为快速求解摄动方程并建立显式灵敏度矩阵表达式， 进一步引入插值算子和投影算子确定离散方程的解， 这样能够同时计算所有发射天线在各个接收器上电场与磁场的显式灵敏度.最后， 针对参数化电导率模型与像素电导率模型分别给出灵敏度矩阵的计算结果， 研究考察海洋可控源电磁测量的空间探测特征.

2 基本原理

本节主要研究电场耦合势海洋可控源电磁响应三维有限体积法离散与直接法求解、插值算子和投影算子、摄动方程离散与求解技术以及像素电导率模型和分块常数电导率模型空间中显式灵敏度快速算法.

2.1 三维有限体积正演与投影算子

引入满足库仑规范条件 ∇ ·A=0 的矢势A 和标势 φ 后， 可以将非均匀各向同性地层中海洋可控源电磁响应数值模拟表示为求解如下耦合势的Helmholtz 方程(时间变化关系假定为 eiωt)[11，12]:

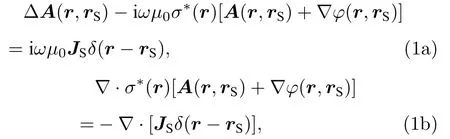
空间任意位置 r 处的电场与磁场强度可以应用如下公式通过方程(1)中的耦合势得到:

为用三维有限体积法求解方程(1)， 选择足够大的计算区域Ω 并在区域外边界 ∂ Ω 上选择简单的截断边界条件×E(r，rS)|∂Ω=0 ， 这时相应的矢势与标势截断边界条件为

基 于Yee 氏 交 错 网 格 Vi+1/2，j，k， Vi，j+1/2，k，Vi，j，k+1/2及Vi，j，k(i=1，··· ，Nx; j =1，2，3，··· ，Ny;k =1，2，··· ，Nz)对计算区域Ω 进行剖分， 同时在各个交错网格的中心分别定义离散矢势分量和以 及 标 势 φi，j，k，并借助三维有限体积法对方程(1)进行离散， 得到如下离散耦合势 A (r，rS) 和 φ (r，rS) 的线性代数方程组[12，14]:

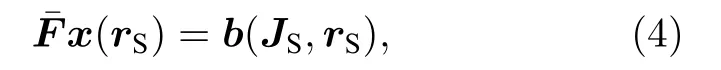
海洋可控源电磁勘探往往采用移动源测量方式， 在同一计算区域Ω 中包含多个不同位置的发射源 JSδ(r-rS，k)，(k =1， 2， ··· ，K) ， 为提高多发射源电磁场数值模拟效率， 将计算区域Ω 内所有不同位置 rS，k发射源产生的右端项b(JS，rS，k)，(k =1， 2， ··· ，K) 进 行合并， 形成一个 N ×K 阶的稀疏带状矩阵B¯ =(b(JS，1，rS，1)，b(JS，2，rS，2)，··· ，b(JS，K，rS，K))， 同时将所有发射源产生的离散耦合势A 和φ也组合起来， 即 X ¯ =(x(rS，1)，x(rS，2)，··· ，x(rS，K)).因为在同一个计算区域中， 每个发射源对应的方程(1)左边的离散矩阵完全相同， 利用方程(4)的离散结果可以得到所有移动源耦合势满足的方程为

利用直接法求解器PARDISO[36]计算出离散矩阵的逆并代入方程(5)， 可以同时计算出所有发射源离散耦合势X¯ =(x(rS，1)， x(rS，2)，··· ，x(rS，K))的数值解:

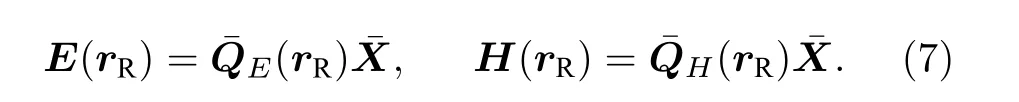
将方程(6)代入方程(7)中并整理， 得到由方程(5)右端项直接计算接收点 rR处的电场与磁场强度的转换公式:

其中，

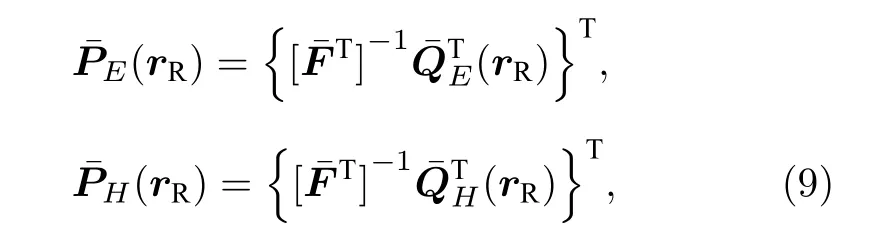
分别称为电场和磁场投影算子.

在海洋可控源电磁勘探中 L ≪K (即接收器个数远少于发射源个数)， 由方程(9)计算投影算子所花费的时间远远小于直接应用方程(7)计算离散耦合势的时间， 因此， 通过引入投影算子(9)能够有效提高整个的正演模拟效率.

2.2 摄动方程求解与显式灵敏度

为计算海洋可控源电磁响应显式灵敏度矩阵，应用摄动原理可以由方程(1)得到电导率微小摄动量 δ σ(r) 引起的耦合势变化 δ A(r，rS) 和δφ(r，rS)满足的方程:

图1 地层模型、像素和分块电导率模型示意图 (a)非均质地层模型与剖分网格; (b)像素电导率模型; (c)分块常数电导率模型Fig.1.Formation model and two different model spaces: (a) Inhomogeneous formation model and grids; (b) pixel model; (c) block model.

以及截断边界条件:

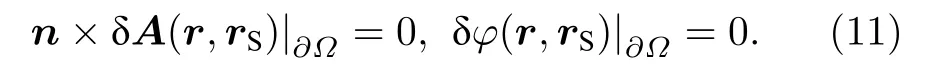
方程(10)的右端项δJ(r，rS)=δσ(r)E(r，rS)是电导率微小摄动产生的散射电流密度.对比耦合势摄动方程(10)与耦合势正演方程(1)可以看出，除右端项不同外， 两者其他部分完全相同， 因此，在散射电流密度已知的情况下， 可采用与方程(1)完全相同的方法求解方程(10).

为便于研究散射电流密度对电磁场的影响、有效计算显示灵敏度矩阵， 假定地层模型由已知电导率为 σS(r) 层状地层形成的围岩和多个电导率不同的异常体组成.图1 是非均质地层模型、Yee 剖分网格上像素电导率模型与分块常数电导率模型示意图.其中， 图1(a)表示电导率为 σS(r) 的围岩和多个电导率分别为 σBlock，γ(r)，(γ =1， 2，··· ，Γ) 、空间分布范围为 Vγ，(γ =1，2，··· ，Γ) 的三维块状异常体.图1(b)和图1(c)分别是像素电导率模型和分块电导率模型在Yee 氏交错网格上电导率的空间分布情况， 在像素电导率模型中(图1(b))， 每个像素单元 Vi，j，k均有一个独立的电导率， 而在分块电导率模型中(图1(c))， 每个块状体内的所有像素单元的电导率完全相同.下面针对图1(b)和图1(c)两种不同的电导率模型， 分别研究建立方程(10)右端项的离散方法以及相应的显式灵敏度快速算法.

2.3 像素电导率模型中的显式空间灵敏度

对于图1(b)中的像素电导率模型， 为简单起见， 将Yee 氏交错网格中的整数网格作为基本像素单元， 并假定围岩电导率保持不变， 而电导率异常体中的所有基本像素单元由M 个整数剖分网格组成， 即 Viα，jα，kα，(α=1， 2，··· ，M) ， 其像素电导率为 σiα，jα，kα，(α=1， 2，··· ，M) ， 这时在像素电导率模型中， 各个异常体上电导率摄动量的空间分布可以表示为如下分片常数函数形式:

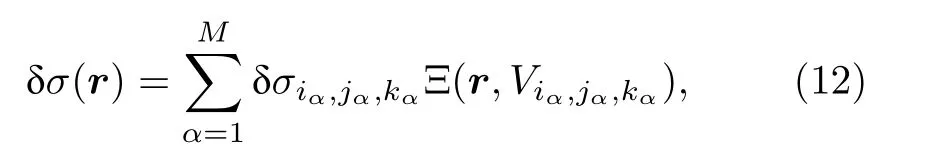
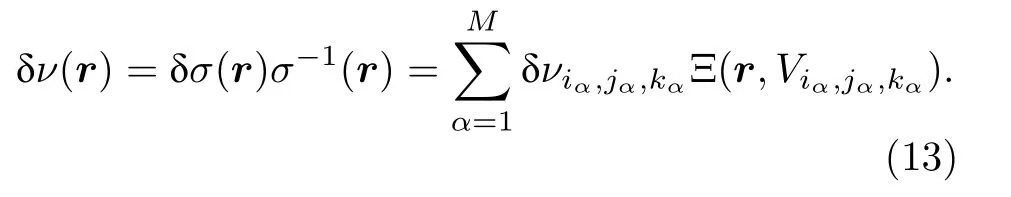
这时， 因电导率摄动产生的散射电流可以看作是如下一系列电偶极子元的叠加:

将方程(14)代入方程(10a)中， 并分别在半整数单元 Vi+1/2，j，k， Vi，j+1/2，k和 Vi，j，k+1/2上计算其体平均，则得到右端项离散向量的各个分量[12]:

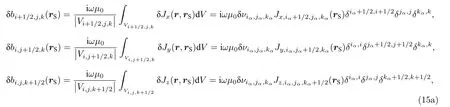
对(15)式的离散结果进行适当整理并将其右端项的离散向量表示成矩阵的乘积形式:， 其 中， h 是 对 应 单 元 的 宽 度，δν=(δνi1，j1，k1， δνi2，j2，k2， ··· ， δνiM，jM，kM)T是M 个像素电导率相对摄动量组成的M 维列向量，是 (15)式中的离散系数经过适当组合后得到的N × M 阶矩阵.这时， 方程(10)在(11)式的边界条件下的离散结果可表示为如下线性方程:

这里， δ X(rS) 是像素电导率相对摄动向量 δ ν 引起的离散耦合势微小变化， 为N × M 阶未知矩阵， 而是方程(10)左端的离散矩阵， 并且与方程(5)中的离散矩阵完全相同.利用方程(9)中的电场和磁场投影算子， 从方程(16)可以得到电磁场强度微小变化与像素电导率相对摄动向量间的线性关系:

这里

是 3 ×M 阶复矩阵， 表示 rS处的发射天线在接收点rR处电场强度与磁场强度像素显式灵敏度矩阵， 灵敏度矩阵中每个元素反映出单元 Viα，jα，kα中电导率相对变化量 δ νiα，jα，kα，(α=1， 2， ··· ，M) 对电磁场各个分量的定量影响.

这里特别需要指出的是， 在进行像素灵敏度矩阵计算或进行像素反演时， 像素单元总数M 可能达到十万次以上的量级， 而网格节点上未知离散矢势和标势总数N 达到百万次的量级.例如若像素总数 M =40×40×56=89600 个， 离散矢势和标势总数 N =1857844.如果直接从线性化方程(16)出发， 确定 δ X(rS) 和像素电导率相对摄动向量 δν 间的显式线性关系再通过插值方法计算各个接收器上电场和磁场显式灵敏度， 则必须先计算出N × M 阶的大型复矩阵和N × M 阶复矩阵的 乘积计算工作量是十分巨大的， 消耗的CPU 时间往往也是难以承受的.而通过方程(9)的投影算子以及(18)式计算电场和磁场的显式灵敏度， 只需要进行3 × M 阶复矩阵与离散右端项N × M 阶复矩阵的乘积， 大大减少了中间的计算过程.此外， 需要说明的是投影算子只与接收点的位置有关， 因此， 可以根据接收点位置事先计算出并反复使用， 而复矩阵只需要利用各个像素单元上电流密度值通过方程(15)就能够快速确定， 所以在正演过程中只需增加一项复矩阵的计算， 然后通过方程(8)和方程(18)就能够同时得到各个测点上的电磁场与电磁场的显示灵敏度， 这种显式灵敏度的快速算法为三维非线性反演建立了非常有利的研究基础.

2.4 分块常数电导率模型中的显式灵敏度

对于图1(c)中分块常数电导率模型， 各个块状异常体 Vγ，(γ =1，2，··· ，Γ) 内部的电导率假定为常 数 σBlock，γ， 其电导率相对摄动量 为δνBlock，γ=δσBlock，γ/σBlock，γ， 这时由于各个异常体电导率摄动导致的地层电导率相对摄动量的空间分布也可表示分片常数函数形式:

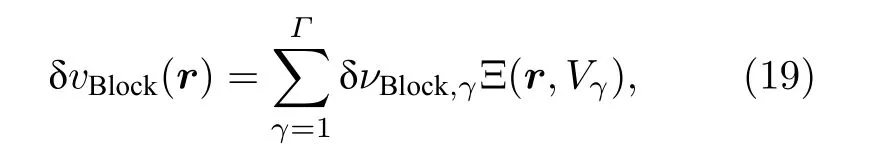
这里 Ξ (r，Vγ) 是块状异常体 Vγ上的特征函数.此外， 为了便于计算， 因为块状异常体电导率摄动对电磁场的影响， 假定异常体 Vγ中包含的像素单元为这时方程(10)右端的散射源可近似表示为

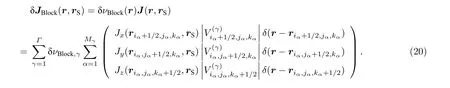
采用与方程(14)类似的离散方法， 可以得到块状体模型中右端项的离散公式:

与方程(14)右端项类似， 方程(21)的离散结果也可表示成矩阵形式:其中， δ νBlock=(δνBlock，1， δνBlock，2， ··· ， δνBlock，Γ)T是Γ 个块状异常体上电导率相对摄动量组成的Γ 阶列向量，是 (21)式中的离散系数组合形成的 N ×Γ 阶已知矩阵.因此， 分块常数电导率模型中各个异常体电导率相对摄动对离散耦合势微小变化影响也可以表示为线性代数方程:

其中， δ XBlock(rS) 是 N ×Γ 阶未知数矩阵， 其每个列向量对应于单个块状体电导率相对摄动量引起的离散耦合势的微小变化.采用与方程(17)和方程(18)类似的方法， 引入分块常数电导率模型中显式灵敏度矩阵( 3 ×Γ 阶复矩阵):

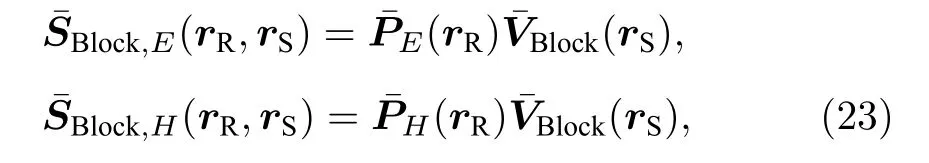
则得到电磁场强度微小变化与块状体模型中各个异常电导率的微小相对摄动量间的线性关系:

2.5 电磁场振幅与相位显式灵敏度

在海洋电磁测量中， 往往以电磁场的振幅与相位作为输出结果， 如x 方向的电场强度常表示为其中AEx(rR，rS)和 θEx(rR，rS) 分 别是 Ex(rR，rS) 的振幅与相位， 可证明电场强度微小变化与其振幅和相位微小变化间的关系为进一步结合方程(17)， 可以得到像素电导率模型空间中电场强度 Ex(rR，rS) 的振幅与相位显式灵敏度矩阵:

以及像素电导率摄动模型空间中电场强度Ex(rR，rS)振幅与相位的线性化响应:

对于磁场强度 Hy(rR，rS) 的振幅与相位的显式灵敏度矩阵与线性化响应， 以及分块模型中电磁场振幅与相位的显式灵敏度矩阵与线性化响应也可以用类似方法得到.

3 数值结果

本节首先将前面的高效直接求解方法(efficient direct method， EDM)得到的显式灵敏度与有限差分方法(finite different method， FDM)[31]得到的灵敏度进行对比， 验证灵敏度快速算法的有效性.在此基础上利用数值模拟结果进一步研究考察不同收发距情况下分块常数电导率模型空间与像素电导率模型空间中电磁场水平分量 Ex和 Hy的振幅和相位灵敏度， 同时也将进行主测线与旁测线上 Ex振幅相位灵敏度的对比.在下面的数值结果中， 工作频率为0.25 Hz， 发射天线离海底的距离为50 m， 发射源间距为100 m.模型电导率是各向同性的， 包含空气层、海水、沉积层以及异常体， 空气层电阻率为 1 06Ω·m， 海水层厚度为1 km、电阻率为0.3 Ω·m， 沉积层电阻率为1 Ω·m.整个计算区域大小为(100， 100， 100) km， 并且x， y 和z 三个正交方向的离散网格数分别为74， 74 和84 个，离散矢势和标势总数 N =1857844 ， 在整个考察区域内采用均匀网格， 而考察区域外到计算区域边界间的网格间距按对数增加.3 个接收器R1， R2 和R3 分别位于x = —6， —4， —2 km 的海床面上， 发射源在x 轴上的变化范围是—8—8 km， 间距250 m，每条测线有65 个不同位置的发射源， 天线的电偶极矩假定等于1 A·m， 图2 是y = 0 的垂直截面上等间距整数网格、接收点和发射源位置示意图.其中， 异常体在x， y 和z 方向的长度分别为3， 3和0.3 km， 其中心位置为 (0， 0， 1) km， 电阻率为100 Ω·m， 3 个接收点位置固定不动.下面的所有数值结果均是在惠普Z820 工作站上运行的， 内存配置为256 Gb.

3.1 灵敏度快速算法验证

首先对图2 中层状背景电导率中单一异常体模型， 利用EDM 和FDM 两种方法分别计算电场振幅和相位相对于整个异常体的灵敏度.图3(a)和图3(b)是3 个不同位置接收点上电场水平分量Ex振幅与偏移距(magnitude versus offset， MVO)正演曲线和相位与偏移距(phase versus offset，PVO)正演曲线.可以看出， 在3 个接收器位置， 因为源的奇异性， 振幅响应强度最大， 由于电磁场的传播效应， 电场振幅随源距的增加快速衰减， 相位随源距增加也呈现出快速变化.然而， 在高阻异常体的上方及右边附近， MVO 衰减曲线产生轻微的波动效应， 距离异常体更近的接收线圈(R3)上的波动效应更加明显， 此外PVO 衰减曲线也显示出类似的波动效应， 这些都是因为高阻异常体的影响.

图2 三维MCSEM 检验模型与网格剖分示意图(y = 0 截面)Fig.2.Verification model and mesh grid of three-dimensional MCSEM (cross-section of y = 0).

图3 3 个不同位置接收器上电场 E x 分量的MVO 和PVO 曲线以及由EDM 和FDM 计算得到的振幅与相位灵敏度对比图 (a)Ex的MVO 正演结果; (b) E x 的PVO 正演结果; (c) E x 振幅灵敏度对比; (d) E x 相位灵敏度对比Fig.3.The E x magnitudes (MVO) and phases (PVO) of 3 receivers at different positions and comparison of Fréchet sensitivity obtained by two different algorithms of EDM and FDM: (a) MVO of E x ; (b) PVO of E x ; (c) comparison of E x amplitude sensitivity; (d) comparison of E x phase sensitivity.

为了定量考察高阻异常体微小摄动引起的水平电场振幅以及相位变化， 同时用EDM和FDM 计算了块状体模型中水平电场振幅显式灵敏度与相位差显式灵敏度这 里 的表 示 异 常体电导率的相对摄动量.图3(c)和图3(d)分别是EDM 和FDM 计算得到的MVO 和PVO 灵敏度变化曲线.其中， EDM 得到的灵敏度结果由3 种不同类型的线表示， FDM 得到的灵敏度结果由3 种不同类型的离散符号表示.从图3(c)和图3(d)可以看出， 两种不同方法得到的灵敏度曲线符合得非常好， 两种方法最大相对误差不超过2%， 从而证明了EDM 在计算显式灵敏度方面的有效性.此外， 从显式灵敏度曲线可以清楚看出接收点位置与发射天线的偏移距对水平电场灵敏度的影响非常明显， 例如R1 接收器由于离异常体的水平距离最远， 其灵敏度值明显小于另两个离异常体较近的接收器R2 和R3 上水平电场灵敏度.此外， 从灵敏度曲线的大小可以看出， 发射天线位于异常体中心右上方0—5 km 范围内， 灵敏度最大， 应用这个区段的测量结果进行异常体反演或对异常体电导率变化进行检测， 效果会更好.

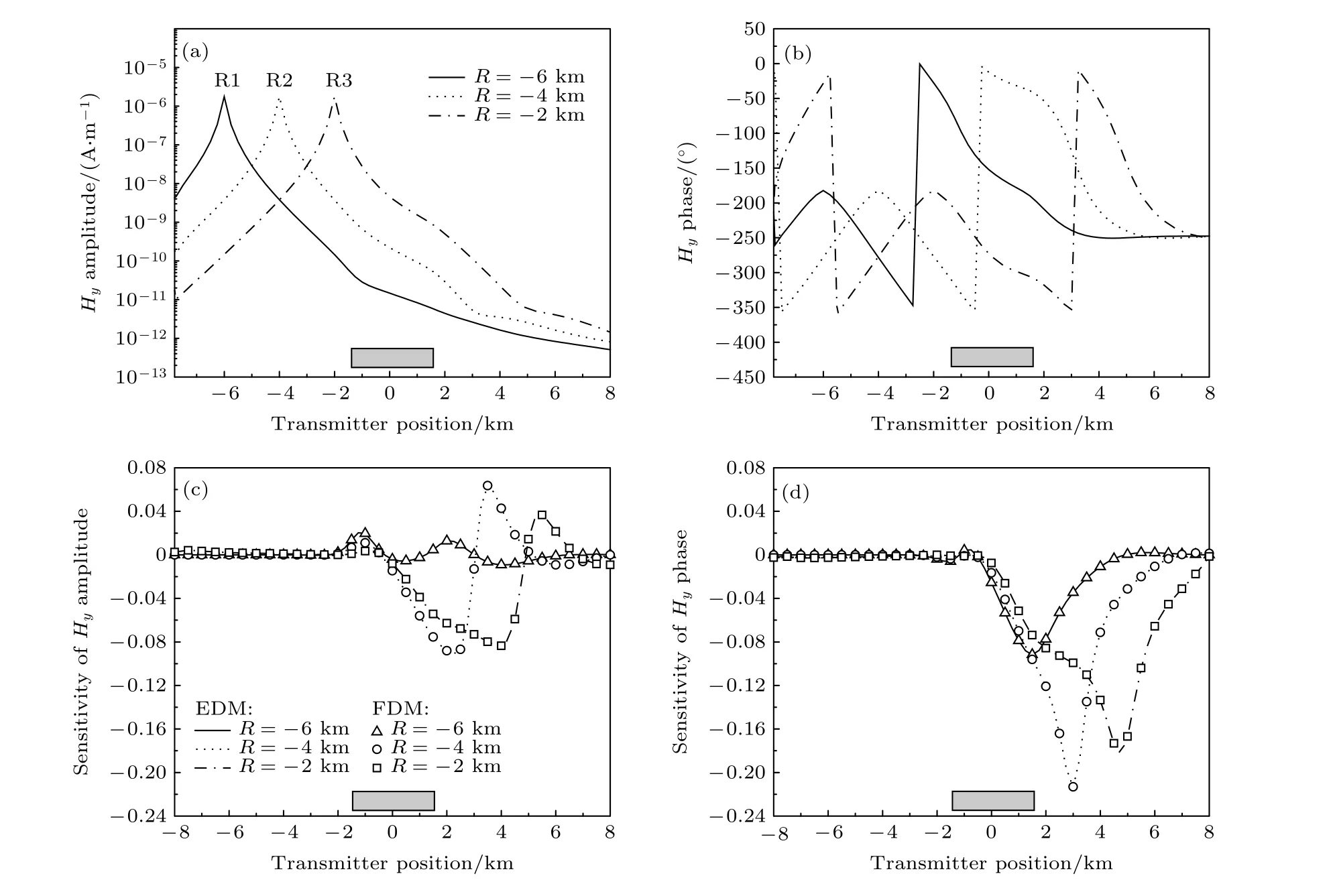
图4 3 个不同位置接收器上磁场 H y 分量MVO 和PVO 曲线以及由EDM 和FDM 计算得到的振幅与相位灵敏度对比图 (a)Hy的MVO 正演结果; (b) H y 的PVO 正演结果; (c) H y 振幅灵敏度对比; (d) H y 相位灵敏度对比Fig.4.The H y magnitudes (MVO) and phases (PVO) of 3 receivers at different position and comparison of Fréchet sensitivity obtained by two different algorithms of EDM and FDM: (a) MVO of H y ; (b) PVO of H y ; (c) comparison of H y amplitude sensitivity; (d) comparison of H y phase sensitivity.

图4 (a)和图4(b)是与图3 相同位置接收点上磁场水平分量的 MVO 和PVO 正演曲线.与图3 中电场振幅与相位的变化特征类似， 随着源距增加磁场振幅快速衰减， 同时， 在异常体上方以及右边附近， 可以看到高阻异常体对MVO 与PVO的影响.为了定量考察高阻异常体微小摄动引起的水平磁场振幅与相位变化， 同时用EDM 和FDM 计算了块状体模型中水平磁场振幅显式灵敏度与相位的显式灵敏度图4(c)和图4(d)是两种不同方法计算得到的MVO 和PVO 显式灵敏度正演曲线对比图.其中， EDM 得到的灵敏度结果由3 种不同类型的线表示， 而FDM 得到的灵敏度结果由3 种不同类型的离散符号表示.从图4(c)和图4(d)可以看出， 两种不同方法得到的灵敏度曲线符合得非常好， 两者最大相对误差也不超过2%， 从而进一步证明了EDM 在计算显式灵敏度方面的有效性.此外， 从显式灵敏度曲线可以清楚看出， 接收点位置与发射天线的偏移距对水平磁场灵敏度的影响也非常明显， 例如R1 接收器由于离异常体的水平距离最远， 其灵敏度值明显小于另两个离异常体较近的接收器R2 和R3 上水平磁场灵敏度.从灵敏度曲线的大小可以看出， 发射天线位于异常体中心右上方0—5 km 范围内， 灵敏度最大.对比电场的灵敏度曲线可以看出， 在有效的偏移距范围内(6—10 km)， 磁场的振幅和相位灵敏度高于电场，电场和磁场的相位包含的灵敏度信息均稍多于振幅， 综合应用磁场和相位测量结果进行异常体反演或对异常体电导率变化进行检测， 效果会更好.

表1 列出了利用EDM 和FDM 两种算法计算灵敏度矩阵的计算耗时， 表中第1 和第2 行为3 个接收器时的两种算法的计算耗时， 第3 和第4 行为5 个接收器情况下的计算耗时对比.结果显示，随着发射器接收器的增加， FDM 的耗时明显增加，而EDM 得益于投影算子的采用， 计算耗时几乎没有增加， 所以可以快速计算多源多接收器的结果，体现了算法的高效性.

表1 两种算法的计算耗时Table 1.Computational time cost of EDM and FDM.

3.2 多块状体模型的显式灵敏度

为进一步考察多个块状体情况下， 块状体水平位置以及埋藏深度等对显式灵敏度的影响， 假定地层中存在3 个几何尺寸与电阻率与图2 完全相同的异常体， 中心位置分别为(—3.5， 0， 0.7)， (0， 0， 1.0)和(3.5， 0， 1.3) km.图5 是含3 个块状异常体模型在y = 0 垂直截面上的等效电导率分布、网格剖分以及发射与接收点位置分布图.为简洁起见， 这里仅给出位于R2 位置处的接收器上水平电场 Ex和水平磁场 Hy的振幅、相位分别相对于3 个块状体电导率灵敏度的数值结果.

图6(a)和图6(b)是位于R2 处的接收器电场水平分量 Ex的MVO 和PVO 正演曲线.可以看出， 电场振幅随源距的增加而快速衰减， 然而， 在异常体上方以及异常体右端， 由于3 个高阻异常体的作用， MVO 衰减速度变慢， 从PVO 曲线也可以看到3 个高阻异常体的影响.图6(c)和图6(d)是用EDM 计算得到的MVO 和PVO 分别相对于3 个块状体电导率(Block 1， Block 2 和Block 3)的显式灵敏度曲线.可以清楚地看出， 接收点位置与发射天线的偏移距以及异常体中心深度对水平电场灵敏度影响均非常明显， 异常体Block 1 离接收点最近且中心深度最浅， 相应的灵敏度值最大，而异常体Block 3 离接收点最远且中心深度最深，相应的灵敏度值最小.此外， 从灵敏度曲线还可以看出， 对于每个异常体的灵敏度曲线均存在灵敏度绝对值的最大值， 说明在海洋可控源探测中存在着最佳测量位置， 对应的灵敏度最强.

图5 3 个块状异常体模型在y = 0 垂直截面上的网格剖分与等效电导率分布图Fig.5.Conductivity distribution and mesh grid of computation model including three different blocks at cross-section of y = 0.

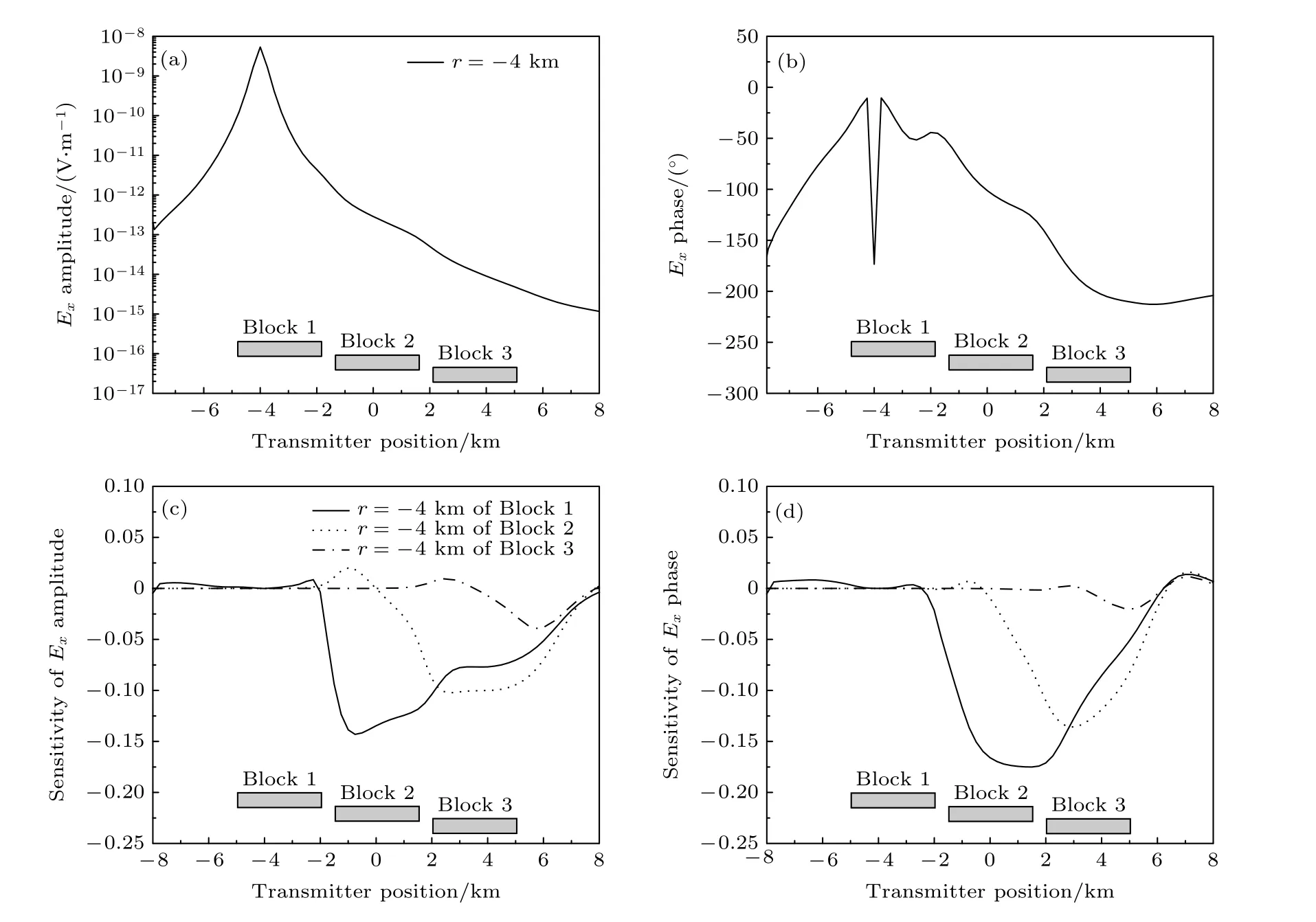
图6 位于R2 处的接收器上 E x 的MVO 和PVO 曲线以及振幅和相位相对于3 个块状体电导率灵敏度 (a) E x 振幅; (b) E x 相位; (c) E x 振幅分别对Block 1， Block 2， Block 3 的灵敏度; (d) E x 相位分别对Block 1， Block 2， Block 3 的灵敏度响应Fig.6.Magnitudes (MVO) and phases (PVO) versus offset of E x at receiver R2 and Fréchet sensitivity about three different Blocks: (a) MVO of E x ; (b) PVO of E x ; (c) sensitivity of E x amplitude about Block 1， Block 2， Block 3; (d) sensitivity ofEx phase about Block 1， Block 2， Block 3.

图7 (a)和图7(b)是位于R2 处的接收器磁场水平分量 Hy的MVO 和PVO 正演曲线.可以看出， 磁场振幅随源距的增加而快速衰减， 然而， 在异常体上方以及异常体右端， 由于3 个高阻异常体的作用， MVO 衰减速度变慢， 从PVO 曲线也可以看到3 个高阻异常体的影响.图7(c)和图7(d)是用EDM 计算得到的MVO 和PVO 分别相对于3 个块状体电导率(Block 1， Block 2 和Block 3)的显式灵敏度曲线.同样可以看出， 接收点位置与发射天线的偏移距以及异常体中心深度对水平磁场灵敏度影响均非常明显， 但有别于电场灵敏度结果， 异常体Block 1 虽然离接收点最近且中心深度最浅， 相应的磁场灵敏度也是最早出现， 但其灵敏度响应峰值小于异常体Block 2， 而异常体Block 3虽然离接收点最远且中心深度最深， 其磁场响应灵敏度值最小， 但峰值非常接近Block 1， 明显好于对应的电场灵敏度结果， 说明磁场的最佳探测深度和探测范围要大于电场.同时， 综合对比电场和磁场的数值模拟结果可以发现， 电场和磁场灵敏度的异常响应范围会随着异常体埋深、收发距的增加而逐渐减小， 磁场灵敏度的值对异常体的响应要大于电场灵敏度的值， 磁场灵敏度曲线的峰值明显大于电场灵敏度峰值， 但灵敏度曲线大于零的持续范围比电场灵敏度的范围要小.由于磁场比电场的灵敏度更大， 更快速达到最大峰值， 因此选用磁场进行电导率动态监测效果可能会更好.此外， 从灵敏度曲线还可以看出， 对于每个异常体的灵敏度曲线均存在灵敏度绝对值最大值， 说明在海洋可控源探测中存在着最佳的测量位置， 对应的灵敏度最强.

图7 位于R2 处接收器上磁场 H y 分量的MVO 和PVO 曲线以及振幅和相位相对于3 个块状体电导率灵敏度 (a) H y 的MVO曲 线; (b) H y 的PVO 曲 线; (c) H y 振 幅对Block 1， Block 2， Block 3 的灵敏度; (d) H y 相位对Block 1， Block 2， Block 3 的灵敏 度Fig.7.The magnitudes (MVO) and phases (PVO) versus offset of H y at receiver R2 and Fréchet sensitivity about three different Blocks: (a) MVO of H y ; (b) PVO of H y ; (c) sensitivity of H y amplitude about Block 1， Block 2， Block 3; (d) sensitivity ofHy phase about Block 1， Block 2， Block 3.

3.3 像素电导率模型空间中的灵敏度

下面进一步考察单一异常体模型上像素灵敏度的空间分布， 了解不同位置的像素电导率相对摄动对电磁响应的影响.限于篇幅， 这里仅给出水平分量 Ex的相关结果.图8 给出了海洋地电模型和像素变化范围， 其中图8(a)是主测线(y = 0)垂直截面上， 接收器、发射源、异常体以及x 和z 方向上的像素分布， 图8(b)是像素空间、异常体以及3 条测线在xy 平面上的投影.x 和y 方向上像素数均等于40 且尺寸均为250 m， 而z 方向的像素个数是56， 像素高度为50 m， 整个像素在x， y 和z三个方向上空间变化范围是(-5， 5)×(-5， 5)×(0.3， 3) km， 像素总数M =40×40×56=89600个.其中主测线位置为y = 0， 两条旁测线的位置分别为y = 1 km 和y = 2 km.3 条测线上接收点的位置固定不变， 坐标分别为(—4， 0， 0)， (—4， 1， 0)和(—4， 2， 0) km.计算该模型显式灵敏度与正演结果总共消耗CPU 时间是1 小时28 分， 占用的最大内存为139.61 Gb.

在计算像素灵敏度之前， 首先给出3 条测线上水平电场 Ex的MVO 和PVO 曲线(图9(a)和图9(b)).可以看出， 由于3 条测线的位置差异， 这3 条不同测线产生的MVO 和PVO 曲线在异常体右侧附近(0—4 km)产生明显偏差， 在远离异常体区域， 不同测线产生的差异逐渐减小.图9(c)和图9(d)是3 条测线上水平电场 Ex的振幅与相位的块状体显式灵敏度变化曲线， 在收发距位于2—10 km 的范围内， 主测线和旁测线上灵敏度均较为明显， 但仔细比较可以看出， 相位灵敏度受测线位置影响更明显， 这与不同测线上PVO 的差异加大完全符合.与块状体灵敏度类似， 像素灵敏度空间变化特征受收发距的影响也较大.

图8 三维MCSEM 模型像素划分与多测线位置示意图 (a) y = 0 截面; (b) 俯视示意图Fig.8.Pixel mesh and survey lines of three dimensional MCSEM model: (a) Cross-section of y = 0; (b) top view.

图9 3 条不同测线时 E x 振幅和相位以及相对于块状异常体的灵敏度对比 (a)振幅; (b)相位; (c)不同测线上振幅灵敏度;(d)不同测线上相位灵敏度Fig.9.Comparison of magnitudes (MVO)， phases (PVO) and Fréchet sensitivity versus offset of E x obtained by three different survey lines: (a) MVO of E x ; (b) PVO of E x ; (c) comparison of E x amplitude sensitivity; (d) comparison of E x phase sensitivity.

根据图9(c)和图9(d)中块状体灵敏度曲线的变化特征， 在3 条测线上均选择x = 4 km 作为发射源的位置， 利用每条测线上固定的发射与接收位置， 计算出 Ex振幅和相位的像素灵敏度， 图10 是3 条测线上电场振幅和相位的像素灵敏度在垂直截面上的灰度图， 可以看出， 发射与接收点周围的像素灵敏度最强， 产生这一现象的主要原因是发射源周围的电场较强， 其周围各个像素单元上电导率的微小摄动会产生较强的散射电流， 引起空间电磁场的更大变化， 而接收点附近的电磁场虽然并不十分强， 但由于其周围像素单元离接收点距离较近，像素单元中的散射电流对接收点上电磁场的影响也会较大.

在远离发射与接收点位置的其他像素单元上，在异常体边界附近以及高阻异常体内部的单元网格上的像素显式灵敏度明显比异常体外面低阻围岩中的灵敏度的值大， 反映出海洋可控源电磁勘探对高阻异常体具有较强的探测能力.此外， 对比3 条不同测线上像素灵敏度的空间分布可以看出，因为y = 0 和y = 1 km 的垂直截面均穿过高阻异常体， 两个不同垂直截面上空间灵敏度分布特征非常相似， 而y = 2 km 的垂直截面已经在高阻异常体的外面， 该垂直截面上灵敏度空间分布与另两个穿过异常体的截面上灵敏度存在着非常大的差异.

为进一步研究水平截面上空间灵敏度的分布情况， 图11 给出了z = 0.3， 0.6 和1 km 三个不同深度的水平截面上像素灵敏度的空间分布， 这里的发射和接收点均位于主测线且与图10 中主测线上发射和接收点位置相同.在z = 0.3 和0.6 km 的水平截面上， 由于发射与接收点位置离水平截面比较近， 发射与接收点周围的灵敏度非常大， 此外由于z = 0.6 km 的水平截面更接近高阻异常体上边界(0.85 km)， 可以看到高阻异常与边界附近单元上的灵敏度有明显显示.而在z = 1.0 km 的水平截面上， 由于发射与接收点位置离水平截面较远， 且水平截面穿过了高阻异常体， 灵敏度的空间分布充分地反映出高阻异常体的位置.可以看到， 像素灵敏度能够更好地展示灵敏度的空间分布规律和特征原因， 在灵敏度空间分布中， 发射机和接收器对灵敏度的影响等同， 灵敏度最佳区域分布在收发器之间， 并随着深度的增加逐渐衰减， 异常体由于其高阻特性， 在异常体内部区域， 灵敏度有一定程度的降低， 而在异常体边界区域， 由于感应电流的影响， 灵敏度有明显的提高， 同样地， 空间灵敏度分布也显示出相位包含的信息稍多于振幅.

图10 发射和接收天线固定在不同截面情况下， 主测线和两条旁测线在垂直截面上 E x 振幅和相位的像素灵敏度空间分布( r S =(4000， 0， -50) m 和 r R =(-4000， 0， -50) m) (a) E x 振幅灵敏度; (b) E x 相位灵 敏度Fig.10.The xz cross-sections along inline and two sidelines of E x pixel sensitivity distribution for a given source-receiver combination( r S =(4000， 0， -50) m and r R =(-4000， 0， -50) m): (a) Sensitivity of E x amplitude; (b) sensitivity of E x phase.

图11 发射和接收天线固定在不同截面情况下， 3 个不同深度的水平截面上 E x 振幅和相位的像素灵敏度空间分布(rS =(4000， 0， -50) m 和 r R =(-4000， 0， -50) m) (a) E x 振幅灵敏 度; (b) E x 相位灵敏度Fig.11.The xy cross-sections at different depth of E x pixel sensitivity distribution for a given source-receiver combination( r S =(4000， 0， -50) m and r R =(-4000， 0， -50) m): (a) Sensitivity of E x amplitude; (b) sensitivity of E x phase.

4 结 论

本文基于电场耦合势Helmholtz 方程的三维有限体积法与直接法求解技术， 并结合摄动理论研究建立了一套三维海洋可控源电磁响应显式灵敏度矩阵的快速算法， 能够针对像素和分块两种不同的电导率模型有效地确定电导率微小摄动与电磁响应微小变化间的线性关系.

在正演过程中， 利用直接求解器得到离散矩阵的逆并结合接收器位置事先计算出插值算子和投影算子， 由于插值算子和投影算子与发射源位置无关， 而仅仅与离散矩阵的逆矩阵和接收器位置有关， 通过投影算子与发射源离散向量的乘积就可以快速确定每个接收点上的电磁响应， 有效提高了多发射源电磁场数值模拟的效率.

不论是在像素电导率还是分块电导率模型中，利用Yee 氏交错网格可以将电导率摄动量表示为剖分网格上的分块常数函数， 每个剖分网格上电场强度与电导率相对摄动量的乘积可以作为散射电流元， 在一阶Born 近似情况下， 散射电磁场实质上可以看作各个剖分网格上所有散射电流元的叠加， 因此， 整个散射电磁场被转换为多发射源电磁场的叠加， 利用投影算子和每个散射电流元离散向量的乘积可以快速获得电磁场微小变化与电导率相对摄动间的线性关系， 得到显式灵敏度计算结果， 从而大大提高了散射电磁场的计算效率.

数值结果显示， 块状体灵敏度能够更好地评估接收器发射源的偏移距与异常体探测能力的变化规律， 对于单个异常体模型， 在0.25 Hz 工作频率下， 电场和磁场有效灵敏度的最大偏移距可以达到10 km 左右， 最小偏离距与接收器到异常体边界的距离有关， 变化范围为2—6 km.对于多个异常体模型， 利用块状体灵敏度可以快速分析考察不同收发距情况下电磁场响应特征、确定最佳的接收器发射机组合.此外， 多个数值模型的计算结果均显示， 在有效的偏移距范围内， 磁场的振幅相位灵敏度高于电场， 相位包含的灵敏度信息稍多于振幅.像素灵敏度能够展示灵敏度空间分布规律和特征， 从灵敏度空间分布中确定出最佳探测区域.