直升机平尾纵向气动特性计算与试验相关性分析

龙海斌，吴裕平

(中国直升机设计研究所，江西 景德镇 333001)

0 引言

直升机在飞行过程中，平尾对保持俯仰方向上的稳定性有重要作用，通常依靠平尾来保持飞行过程中的迎角和速度静稳定性[1]。同时，平尾对直升机的姿态角影响也比较大[2]。因此，在直升机研制过程中需要获得比较全面的平尾气动特性数据。其中侧滑状态的平尾纵向气动特性数据在直升机飞行品质和载荷等计算过程中应用比较多[3]。目前主要采用风洞试验和CFD计算的方法来获得平尾纵向气动特性数据[4]。风洞试验在航空航天等领域的应用时间比较长久，基于风洞试验结果的设计方法和流程也已经在多个型号中应用，具有非常高的可靠性和可信度。但是风洞试验需要设计和制造风洞试验模型，有时还需要等待风洞试验室的档期，并且在风洞试验过程中修改气动外形比较困难。随着计算机技术和数值计算方法的发展，CFD计算方法在多个领域获得了比较多的应用。在多个直升机型号研制过程中也采用CFD方法对机身、平尾和垂尾等部件的气动特性进行计算。文献[5]采用CFD计算方法对某型共轴式直升机的上平尾和下平尾的升力和俯仰力矩特性进行了计算与分析。在得到CFD计算结果之后，通常会将CFD计算值与风洞试验结果进行对比分析[6]。针对直升机平尾和垂尾等的气动特性CFD计算值与风洞试验结果的对比分析，文献[7]对AH-64直升机基本机身+“狗窝”和基本机身+“狗窝”+平垂尾等状态进行了风洞试验和CFD计算，研究了平垂尾对机身阻力的影响，并对比了阻力的CFD计算值和风洞试验结果。文献[8]采用两种CFD方法对某型无人直升机的平尾和垂尾等的气动特性进行了计算，并与风洞试验结果进行了对比分析。文献[9]分别对S-97共轴高速直升机的孤立机身和孤立机身+平垂尾的气动特性进行了CFD计算分析，并与风洞试验结果进行了对比分析，求解过程采用笛卡尔网格划分。文献[10]对两型直升机的平尾大攻角气动特性的CFD计算值与风洞试验结果之间的相关性进行了研究。CFD计算模型包括全尺寸模型和缩比模型。本文采用CFD计算方法对侧滑状态时某无人直升机的选定机身状态气动特性进行了计算，提取出了平尾纵向气动特性，并与风洞试验结果进行了对比分析。之后分别采用增量法和比值法对平尾纵向气动特性CFD计算值与风洞试验结果之间的相关性进行了分析。

1 风洞试验

某型直升机平尾气动特性试验在某回流式风洞中进行。本次风洞试验所在试验段的截面为扁八角形，主要尺寸为3m×2.5m。风洞试验过程中采用腹部支撑方式安装试验模型。靠近机身腹部一侧的支架为两根圆柱支杆，靠近风洞地板一侧的支架安装了翼型截面整流罩。受风洞试验段截面尺寸的限制，风洞试验模型采用缩比模型。风洞试验过程中采用塔式六分量机械-应变天平测量阻力、升力和俯仰力矩系数。机械-应变天平的量程比较大，运行过程中受外界电磁干扰等影响比较小。在风洞试验过程中采用增量法来获得平尾的气动特性数据。即首先进行选定机身状态的风洞试验；之后将平尾拆除，即去平尾状态，再进行去平尾状态的风洞试验；最后将选定机身状态的气动特性数据减去去平尾状态的气动特性数据，即得到平尾的气动特性数据。得到的风洞试验数据进行了支架干扰修正和洞壁干扰修正。支架干扰修正采用镜像两步法，洞壁干扰修正包含分离流和阻塞修正。

2 CFD计算

2.1 计算模型

在进行网格划分之前首先要选定计算模型。CFD计算模型以机身、平尾等部件的几何理论外形为基础，同时考虑风洞试验模型的设计特点等。对部分比较小的空和缝隙等进行修理，以方便后续网格划分。本次CFD计算模型采用缩比模型，尺寸与风洞试验模型尺寸一致。选定机身状态和平尾的CFD计算模型如图1所示。选定机身状态包括机身、主桨毂、起落架、尾梁、垂尾和平尾等部件，其中平尾布置在垂尾顶部，为T型平垂尾布局。

2.2 网格划分

网格划分是CFD计算中的一项重要工作，通常要占用整个CFD计算60%左右的人力资源和工作时间。目前常用的网格有结构网格、非结构网格等类型。由于机身外形比较复杂，因此本次计算采用非结构网格划分，划分方法为八叉树。该方法首先用一个方体覆盖整个计算域；之后不断细分为八个小的方体，直到满足相应的空间和表面网格尺寸的设定值；最后将各方体划分为四面体。为了提高CFD计算结果的准确性，对平尾前缘和后缘等区域的面网格尺寸设置得比较小，这些区域划分得到的四面体网格也比较细。平尾部分的网格划分如图2所示。

图1 选定机身状态和平尾CFD计算模型图

图2 平尾网格划分示意图

2.3 数值求解

空气流动的控制方程为N-S方程。目前求解N-S方程的方法主要有雷诺平均(RNAS)、大涡模拟(LES) 、直接数值模拟(DNS)和格子玻尔兹曼(LBM)等。其中,雷诺平均方法占用内存比较少，计算速度也比较快，同时计算结果的准确性和可靠性等都基本满足工程应用的需求,因此在直升机机身等部件的气动特性计算中应用比较广泛。

雷诺平均方法求解N-S方程的基本思想是，首先将满足动力学方程的湍流瞬时运动分解为平均运动和脉动运动两部分，之后通过雷诺应力项的模化来体现脉动运动部分对平均运动的贡献，即通过湍流模型来使得N-S方程封闭，从而进行求解。常用的湍流模型有一方程S-A模型、二方程k-ε模型、k-ε模型和SST模型等。其中S-A模型能很好地处理低雷诺数流动中粘性影响的边界层区域，在航空领域应用比较广泛。该模型增加的输运方程如下：

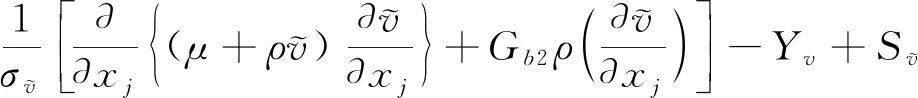
(1)

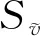
在划分网格之前对平尾部分进行单独命名，完成CFD计算之后从计算结果中取出单独平尾的纵向气动特性结果。在计算过程中设置计算域的边界为压力远场条件，设置来流速度为60m/s，与风洞试验过程中的来流速度一致。首先计算0°侧滑角时的纵向气动特性，之后不断增大侧滑角。

3 结果对比分析

采用CFD方法分别计算了无侧滑(β=0°)、小侧滑(β=8°)、中等侧滑(β=16°)和大侧滑(β=32°)状态的平尾纵向气动特性，包括阻力、升力和俯仰力矩特性，并与风洞试验结果进行了对比，如图3所示。

图3 平尾纵向气动特性计算与试验结果对比图

从整个图中可以看出，平尾纵向气动特性的CFD计算值与风洞试验结果随攻角和侧滑角的变化趋势一致。从图3(a)中可以看出，平尾阻力系数的CFD计算值随攻角的变化比较光顺，而风洞试验结果随攻角的变化有一定的跳跃。这是由于在攻角比较大时，风洞试验模型的部分区域存在流动分离，而目前CFD计算方法对这些分离流动的模拟能力比较弱。在小攻角范围内，各侧滑状态的平尾阻力系数比较接近；随着攻角的不断增大，各侧滑状态的平尾阻力系数有一定的差别。分析图3(b)中的升力系数变化趋势可以发现，在负攻角范围内，随着侧滑角的不断增大，平尾的升力系数不断增大。在正攻角范围内，侧滑角的变化对平尾升力系数的影响比较小。类似地，由图3(c)可以看出，在负攻角范围内，俯仰力矩系数随侧滑角的增大而不断减小。同样地，在正攻角范围内，随着侧滑角的增大，平尾的俯仰力矩系数基本上不变。

4 相关性分析

4.1 增量法分析

首先采用增量法研究平尾纵向气动特性CFD计算值与风洞试验结果之间的相关性，即将平尾纵向气动特性的风洞试验结果减掉CFD计算值，得到两种差值随攻角的变化情况。从图4的整体情况来看，随着攻角绝对值的不断增大，风洞试验结果与CFD计算值之间的差值不断增大。从图4(a)中可以看出，在负攻角范围内，大侧滑状态的差值比较大；而在正攻角范围内，小侧滑状态的差值相对比较大。这是由于在负攻角范围内，两者之间的差值主要是因气动分离引起的，大侧滑状态时的气动分离比较大；而在正攻角范围内，两者的差值主要是机身和主桨毂等对平尾的气动干扰引起的，小侧滑状态时，机身和主桨毂等对平尾的气动干扰比较大。由图4(b)中的升力系数差值变化趋势可以发现，随着攻角的增大，平尾升力系数的差值不断减小。在计算的侧滑角范围内(0°～32°)，随着侧滑角的增大，升力系数差值的绝对值的最大值也不断减小。这是由于平尾的截面为反装的非对称翼型，在负攻角时流动分离更严重。分析图4(c)中的俯仰力矩系数差值变化趋势可以看出，随着攻角绝对值的减小，平尾俯仰力矩系数差值不断减小。在大部分攻角范围内，中等侧滑状态(β=16°)的俯仰力矩系数差值比较小。这是由于无侧滑状态下机身和桨毂等对平尾有气动干扰作用，而在大侧滑状态，平尾处的流动分离比较大。

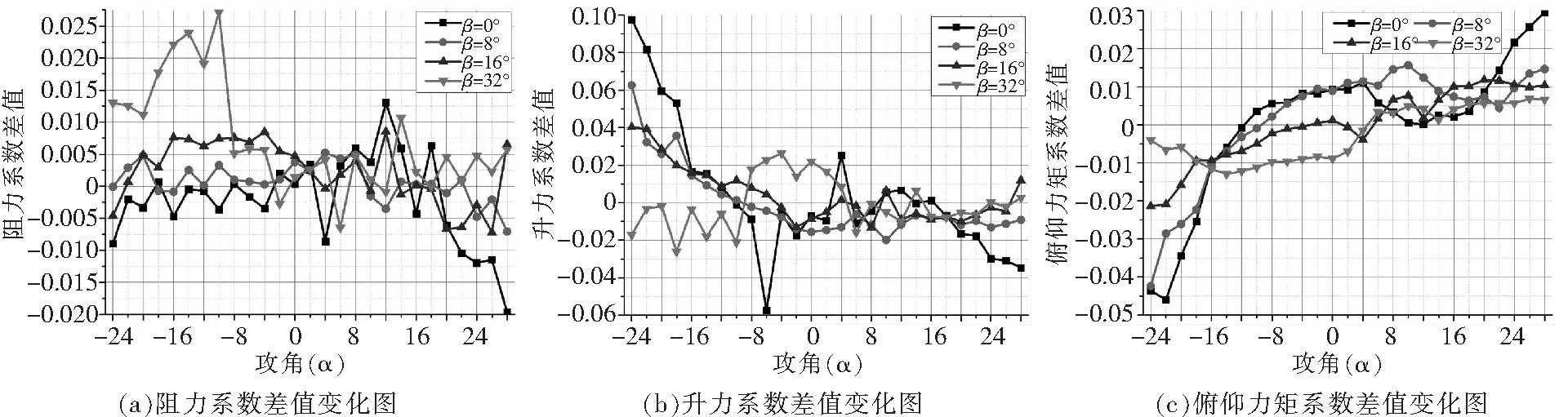
图4 纵向气动特性试验与计算结果差值对比图

4.2 比值法分析

针对CFD计算值与风洞试验结果之间的差异，采用比值法继续分析两者之间的相关性，即将风洞试验结果除以CFD计算值，分析两者的比值随攻角和侧滑角的变化情况。分析图5中的整体变化情况可以发现，在小攻角范围内，风洞试验结果与CFD计算值的比值比较大。这是由于在小攻角范围内，平尾纵向气动特性的值比较小，CFD计算过程中产生的比较小的误差都会导致比值比较大。其中小侧滑状态两者的比值比较小。这是由于在小侧滑状态，机身和桨毂等部件对平尾的气动干扰比较小，同时由于侧滑角相对比较小，气动分离还比较小。因此CFD计算值与风洞试验值比较接近，而且CFD计算结果比较稳定。分析图5(a)中平尾阻力系数的比值可以看出，在负攻角范围内，风洞试验结果与CFD计算值的比值变化大。

5 总结与讨论

通过对某型无人直升机的平尾纵向气动特性进行CFD计算，并采用增量法和比值法对CFD计算值与风洞试验结果进行相关性分析，可得出如下结论：

图5 纵向气动特性试验与计算结果比值对比图

1)目前CFD计算得到的平尾纵向气动特性的变化趋势与风洞试验结果一致，说明CFD方法具有一定的准确性和可靠性。

2)随着攻角绝对值的增大，CFD计算值与风洞试验结果之间的差值不断增大。但是两者之间的比值在小攻角范围内比较大。

3)在小侧滑和中等侧滑状态，CFD计算值与风洞试验结果之间的差值和比值都相对比较小。

4)综合考虑增量法和比值法的分析结果，采用比值法对平尾纵向气动特性CFD计算结果进行修正相对比较合适。