以主题任务驱动大单元学习的结构设计??

摘 要 在数学教学中，可以用主题性任务联结起不同领域的知识，组织新的学习单元。按照主题性任务引领的知识之间、事件之间或故事之间的驱动路径，组建的大单元可以有链式结构、辐射结构、树状结构、嵌入结构等联结方式。

关键词 主题任务 大单元学习 结构设计

崔允漷认为：“一个单元就是一个完整的学习故事，就是一种课程，或者说微课程。譬如语文教材中一个单元主题下的四篇课文，如果不是一个完整的学习方案，没有学习任务的驱动，就只是内容单位。”在数学教学中，我们可以将不同知识领域的知识通过某一主题性任务，组织成新的学习单元。以主题任务驱动大单元学习的结构设计大致有链式结构、辐射结构、树状结构、嵌入结构等联结方式。

一、主题任务驱动大单元学习的链式结构

主題任务引领的大单元设计的链式结构特点是，学生的学习在主题任务的驱动下沿着内在逻辑线或外在情景线循序渐进，形成一种链环式的套构关系，环环相扣、步步递进，引导学生不断走向知识的深处或故事的结局。

1.着眼核心概念设计大单元主题性任务

脑科学研究发现，人类学习的本质是以模块的方式进行复杂学习。“模块”，通俗地讲就是“概念”，就是以概念为核心生长出各种各样的知识链接。由此，我们可以把数学核心概念或数学基本原理设计成主题性任务，由此生长成一条联结各个“亲缘”知识的流水线，由此延伸出大单元学习。

例如，乘法解决了相同数相加的书写简便问题，乘法口诀则解决了相同数相加的计算快捷问题，当学生明白了知识原理，就可以此为核心理念构造知识，依次把2～9的乘法口诀编写出来。教师只要把起始课作为“种子课”上好，学生就可以在迁移知识的同时迁移学法，按照相同的“知识图纸”把后续乘法口诀创造出来。此时的单元看似还是原来的单元，但它已不再是要靠教师的教来推动的“内容单位”，而是学生在学会方法后主动创造内容的学习单元。这样，学生就不会出现以前那种“单元结束，思考也就结束”的封闭状态，而会继续思考“为什么学到9的乘法口诀就结束了”，进而把多位数乘法等多个知识单元收入同一学习单元，引发后续学习。

2.着眼生活场景设计大单元主题性任务

数学源于生活，又服务于生活。对学生而言，熟悉的衣食住行即是他们的生活，我们可以由此设计“与孩子的现实生活充分联系”的主题性任务，把原来不同领域的知识联结起来，构建学习大单元。

例如苏教版《数学》五年级上册编排有“负数的初步认识”“多边形的面积”“小数的意义和性质”“小数加法和减法”“小数乘法和除法”“统计表和条形统计图”“解决问题的策略”“用字母表示数”8个单元，除了“小数的意义和性质”“小数加法和减法”“小数乘法和除法”外，其他单元相对独立。但如果把它们放置于衣食住行的“真情境”，那么这些内容单位就建立了联系，可以统整于以“小明的农家乐”为主题任务情境的学习大单元：“负数的初步认识”可以与购物的收支联结，“小数的意义和性质”“小数加法和减法”“小数乘法和除法”及“统计表和条形统计图”可以与购物的标价、计价和比价联结;而“多边形的面积”可以与生活中的种植联结，如果镜头切换到种花则可接续到“解决问题的策略”单元“怎样围长方形花圃面积最大”问题。当然，“小数乘法和除法”单元也可以置身这一情境之中。至于“用字母表示数”单元，一位教师采用微信红包开启知识大门：由小明做家务后妈妈奖励微信红包5.20元引出“用具体的数表示已知数”，由未点击的微信红包引出“用字母表示未知数”，由“第三个红包比第二个红包多80元”引出“用字母式表示未知数”……

二、主题任务驱动大单元学习的辐射结构

主题任务引领的大单元设计的辐射结构特点是，以任务主题为中心，向知识空间或生活空间的四面八方伸展开去，从多方面、多角度、多层次丰富素材、丰富认识，最终圆满完成任务目标。

1.转换探究视角设计大单元主题性任务

主题性任务应该是美国康奈尔大学教授乔治·J·波斯纳在《学程设计》所说的“中心问题”，综合布卢姆、加涅、马扎诺等人，以及数学课程标准的表述，小学数学课程可将中心问题整合为技能、鉴赏、探究、创造、实践五种单元导向。

例如苏教版《数学》五年级下册“圆的认识”一课，学生对教师引用诗人但丁“圆是最美的图形”这一表述颇感兴趣也深感困惑：“为何这么说？”我们就以此为中心问题进行辐射拓展，设计以鉴赏性为导向的主题任务，构建大单元学习：（1）走进知识圈，展开“圆的认识”的知识教学;（2）走进生活圈，利用教材新授之后编排的“你知道吗？”上半部分图片，通过欣赏自然现象中大量存在的圆形事物，让学生体会到上帝创造的圆形的美;（3）走进心理圈，辐射拓展到心理学，介绍生活中“人更喜欢圆形物体”的心理学原理;（4）走进艺术圈，利用教材新授之后编排的“你知道吗？”下半部分图片，通过欣赏艺术领域中大量存在的圆形事物，让学生体会到上帝创造的圆形的美;（5）走进文学圈，辐射拓展到文学，组织学生阅读爱默生的散文《圆》……

2.转换应用范围设计大单元主题性任务

生活处处有数学，同一种事物，不同的观察角度、应用范围、研究方式都可能联结不同单元、不同领域，甚至不同学科的知识。也就是说，通过知识载体应用范围的转换也能设计主题性任务，构建大单元学习。

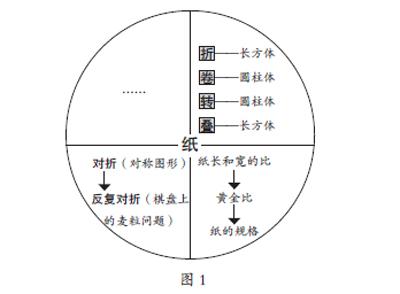
例如我们设计的主题为“纸的学问”的探究任务，通过折、卷、转、叠等操作引出长方体、圆柱体等立体图形，将“长方体和正方体”与“圆柱和圆锥”单元联结成大单元学习;转换应用范围，通过纸张长和宽的比以及纸的规格联结“比和比例”单元，转入数与代数领域的学习;如果再次转换应用范围，就可以通过对折联结到有理数乘方的中学数学知识……（如图1）

三、主题任务驱动大单元学习的树状结构

主题任务引领的大单元设计的树状结构特点是，以任务主题为根，在生长出的每一个知识节点上不断生长出新的知识“枝叶”，由此建构的学习单元越来越大，学生的认知背景越来越丰富，思想收获越来越多。

1.基于知识原点设计大单元主题性任务

学生的学习越是回到知识的源头，对知识的理解越会深刻，也更能清楚辨明知识的发展方向。所以，从知识的原点设计大单元主题性任务，有助于教师提高教学站位，有助于学生看到知识的生长起点和结构化过程。

例如“十进制”的产生很大程度是因为人有10根手指，它把原本分属两个领域的计数单位与计量单位联结起来，把小数的产生与学过的整数联结起来，把长度单位与学过的货币单位联结起来。随后，在纵向生长的一些知识节点上，又可以通过横向生长进入新的知识板块，如相邻面积单位之间的进率是10×10，相邻体積单位之间的进率是10×10×10，与学过的长度单位联结起来。这样联结而成的学习单元的体量将会越来越庞大，知识之树也越来越枝繁叶茂。

2.基于生活常识设计大单元主题性任务

教学不只是让学生学陌生的知识，还应通过拓展性学习让学生看到知识的有用，获得更多的感悟，学到更多的本领。学生的学习除了解决问题，还可以解释问题甚至预测问题。而其中的问题又不只是数学问题，很多还是与数学应用密切相关的生活问题。由此，我们把传统教学的“学以致用”逆向设计成“用以致学”，通过知识的生活应用设计主题性任务，构建新的学习单元。

例如把“为什么生活中自行车架、空调支架都做成三角形的？”这一生活常识作为“多边形的认识”单元的任务主题，学生为了能够完成解释这一问题的任务，就有了学习“三角形的认识”的需要，学完之后得到的结果还无法让人信服，于是为了寻找对比，又踏上了由“平行四边形的认识”“梯形的认识”到一般四边形直至五边形、六边形等多边形的学习之旅。如此，原本“多边形的认识”这一单元的内容便不再孤单，而在为了完美解释生活问题的主题任务引领下不断地伸展和拓展。

四、主题任务驱动大单元学习的嵌入结构

主题任务引领的大单元设计的嵌入结构特点是，在知识学习进程中，遇到障碍，引进必要的技术支援，而所需知识位于其他单元，由此整合成大单元，或为帮助学生学得更好，引进必要的工具支持，而所列知识位于其他单元，由此聚合成大单元。

1.引进关键技术设计大单元主题性任务

教材有时会把知识分解成独立的内容或单元，学生学习这些先行知识时茫然不知其为何用。为了避免这种割裂式学习，我们待到学生需要时才引进必要的知识技术，嵌入相关知识单元的学习，从而整合成一个学习大单元。

例如在“因数和倍数”单元，学生艰涩、迷惑地学习的“通分”，直至转入“分数加减法”单元“异分母分数加减”，才明白通分是其关键技术。为让学生一开始就明明白白学习，我们先教学“分数加减法”单元，在遇到“怎么可以把异分母分数转化成同分母分数”时才引进“分数的基本性质”的教学，之后在进一步思考“怎么可以快速地把异分母分数转化成同分母分数”时再引进“最小公倍数”的教学，这样在完成“异分母分数如何加减”这一主题性任务中实现“分数的基本性质”与“因数和倍数”“分数的加法和减法”等单元的统整。

2.引进辅助工具设计大单元主题性任务

除了着眼核心概念，我们还着力关键能力，设计大单元主题性任务。其中，学会利用思维工具助力知识学习也是一种关键能力。

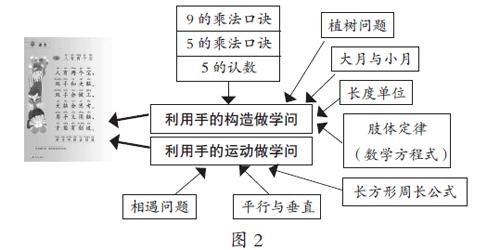
手是人身上最便携的“学习工具”，在每一次知识教学时，我们想一想是否可以借助手帮助学生理解和记忆知识，最终归结到“利用手的构造做学问”和“利用手的运动做学问”两种辅助方式。此中，通过手把原本散落各个单元看似并无关联的众多知识聚集在了一起（如图2）。我们让学生在平时或复习时，以“如何把知识‘手到擒来？”为任务主题，采用知识树或手抄报等形式，把这些内容单位联结成学习大单元，如此学生对学过的语文课文《人有两个宝》有了更深的体会，实现数学学科与语文学科的联结。

美国教师帕克·帕尔默在《教学勇气》一书中写道：“（优秀教师）能编织一个复杂的网，这张网联结着学生、课程以及他们自己。只有这样，学生才能学会为他们自己编织出一个世界。”我们期望通过主题任务驱动的大单元学习，来编织能够联结课内与课外、科内与科外的一个复杂的网，让学生能够为自己编织一个更广阔、更美好的世界。

参考文献

[1] 管国贤，严育洪. 任务驱动式教学在小学数学教学中的应用[J].江苏教育研究，2012（08）.

[2] 严育洪.课堂的突围与开放[M].福州：福建教育出版社，2013.

[3] 严育洪.让学习真正发生——小学数学任务驱动式教学解读与实施[M].济南：山东文艺出版社，2017.

[责任编辑：陈国庆]