Gravity Wave Generated by Initial Axisymmetric Disturbance at the Surface of an Ice‑covered Ocean with Porous Bed

Piyali Kundu · Rumpa Chakraborty

Abstract This paper is concerned with the generation of gravity waves due to prescribed initial axisymmetric disturbances created at the surface of an ice sheet covering the ocean with a porous bottom. The ice cover is modeled as a thin elastic plate, and the bottom porosity is described by a real parameter. Using linear theory, the problem is formulated as an initial value problem for the velocity potential describing the motion. In the mathematical analysis, the Laplace and Hankel transform techniques have been used to obtain the depression of the ice-covered surface in the form of a multiple infinite integral. This integral is evaluated asymptotically by the method of stationary phase twice for a long time and a large distance from the origin. Simple numerical computations are performed to illustrate the effect of the ice-covered surface and bottom porosity on the surface elevation, phase velocity, and group velocity of the surface gravity waves. Mainly the far-field behavior of the progressive waves is observed in two different cases, namely initial depression and an impulse concentrated at the origin. From graphical representations, it is clearly visible that the presence of ice cover and a porous bottom decreases the wave amplitude. Due to the porous bottom, the amplitude of phase velocity decreases, whereas the amplitude of group velocity increases.

Keywords Axisymmetric disturbances and ice-covered ocean · Porous bottom · Laplace and Hankel transform · Method of stationary phase · Free surface depression · Phase velocity and group velocity

1 Introduction

Ocean wave generation or propagation into or within sea ice fields is a well-established research topic that is currently getting the extensive attention of various researchers. Actually,the sea ice of the polar region bears a significant role in global climate and the conservation of marine life. In the polar region,the seawater freezes due to the very low temperature of the atmosphere. Due to less density of ice than water, ice floats on the ocean’s surface so that the ocean is covered by a continuous sheet of ice or broken ice. In recent years the scientific activities in Polar Regions are increasing day by day because,in reality, sea ice covers about 7% of the Earth’s surface and about 12% of the world’s oceans. There are usually two types of models for floating ice exit. In the first model, the ice is considered to consist of non-interacting floating particles, i.e.,broken ice, and in that case, the ocean is said to have an inertial surface (cf, Weitz and Keller 1950; Rhodes-Robinson 1984;Mandal and Mukherjee 1989). In another model, the floating ice is assumed to be in the form of a thin elastic sheet (cf. Fox and Squire 1994; Chung and Fox 2002; Squire 2007; Meylan and Squire 1996 and others). Investigations of such water wave problems have gained reasonable interest due to the effects of internal wave propagation through the marginal ice zone in the arctic regions. Bhattacharjee and Sahoo (2008) analyzed the effect of uniform current on flexural gravity waves generated due to a disturbance such as an initial impulse or an initial depression. Mohapatra and Bora (2009) considered the propagation of oblique waves in a two-layer fluid whose upper layer is bounded above by a thin uniform ice sheet and the lower layer has small bottom undulation. Sturova (2013)derived the velocity potential for a transient source of arbitrary strength in a fluid of infinite depth with an elastic solid cover.The interest behind the study of these problems arises due to their applications in several practice areas, such as large floating plate-like structures, floating airports, etc.

Generally, surface gravity waves are generated due to various kinds of initial disturbances at the surface of an ocean or within the ocean. When a non-spherical shock wave caused by a mid-air blast impinges on the surface of an ocean or some explosion occurs within or above the ocean region,surface waves are generated due to an initial impulsive pressure or initial displacement (elevation or depression). The relevant two-dimensional unsteady motion thus formed was studied in the classical treatises of Lamb (1945) and Stoker (1957), considering the linear theory of water waves.They used the method of Fourier transform and obtained the expression of free surface elevation in the form of infinite integrals, which were then evaluated approximately for large time and distance from the source of the disturbance.These results can be extended in case of any initial surface disturbances across the arbitrary region for uniform finite depth water with a rigid bottom (cf. Wen 1982). Maiti and Mandal (2005) considered the wave generation problem due to initial axisymmetric disturbances on the ice-covered surface of the water. A disturbance is said to be axisymmetric when it is identical in every plane that passes through the axis of a cylinder so that the angular component of the governing equation can be neglected. An axially symmetric disturbance was considered in brief by Kranzer and Keller(1959). They discussed the problem of water waves generated by explosions in the case of three-dimensional unsteady motion in the water of uniform finite depth due to an initial surface impulse or initial surface elevation in a circular area. They also compared their theoretical results with the available experimental results. In the recent past, Banerjea et al. (2011) discussed the wave generation problem due to a line source present in an ice-covered ocean with small bottom undulation. Recently, Das and Mohapatra (2019)considered a particular hydro-elastic model to examine a radiation problem caused by a submerged sphere beneath in an infinitely extended ice-covered sea where the lower surface is enveloped by a flexible base surface. Khuntia and Mohapatra (2020) examined the motion of the fluid in a sea,where the top surface is sealed by a floating ice floe and the bed is of an adaptable type with small distortion. In all of these problems, the authors considered floating ice as a thin elastic plate.

All the aforesaid problems were studied for the ocean with a rigid bottom. In reality, the ocean bottom is composed of porous materials such as rocks, soil, zeolite, biological tissues, etc. However, there is not much work involving the ocean surface covered with a thin ice sheet, and the bottom is composed of some porous materials. So when the water is covered with a thin ice sheet and some porous materials are present at the bottom, the corresponding water wave problems are also of some interest to ocean engineers. There are so many researchers who considered different types of modeling of the problems for the ocean with a porous bottom in the presence of ice-cover. Tsai et al. (2006) studied the problem of wave transformation over a submerged permeable breakwater on a porous slope seabed. They presented several numerical results for the verification of the model and the wave transformation over the submerged breakwater on the porous bottom. Mohapatra (2014) studied the scattering of surface waves by the edge of a small undulation on a porous bed in an ocean with covering thin elastic ice sheet at the upper surface. Paul and De (2014; 2017) considered two types of scattering of plane surface wave problems for the uneven porous bottom, one in a two-layered channel and the other in a three-layered channel. Maiti and Mandal (2014)considered the problem of water wave scattering by a floating elastic plate in an ocean with a porous bed. Gayen and Islam (2018) considered the problem of determining velocity potential due to the presence of a horizontal circular ring in the water of finite depth with a floating elastic plate or a floating membrane at the upper surface and the bottom of the fluid region is composed of the non-dissipative porous medium. Very recently Kundu and Mandal (2019) discussed the generation of surface waves in water with a porous bottom due to various types of prescribed initial axisymmetric disturbances at the free surface. In these problems, the authors consider a special type of porous bottom for which the porosity parameter is taken to be only real and has the dimension inverse of length.

In the present paper, we consider the generation of gravity waves by initial axisymmetric disturbance at the surface of an ice-covered ocean, while the ocean bed is taken to be porous in nature. The problem is formulated as an initial value problem assuming linear theory. Laplace and Hankel transform techniques are used to find the depression of the ice-covered surface in terms of a multiple infinite integral. This multiple integral is approximated by the stationary phase method for two types of initial disturbances namely initial axially symmetric depression or impulse. Finally, the asymptotic form of the ice-covered surface is depicted graphically against a nondimensional distance for a fixed time and against nondimensional time for a fixed distance and different values of nondimensionalized porosity parameter and ice-cover parameters. Also, phase velocity and group velocity of the surface gravity waves are evaluated analytically and numerically. Lastly, appropriate conclusions are drawn for the initial depression of the ice-covered surface and phase velocity, and group velocity of the surface gravity waves.

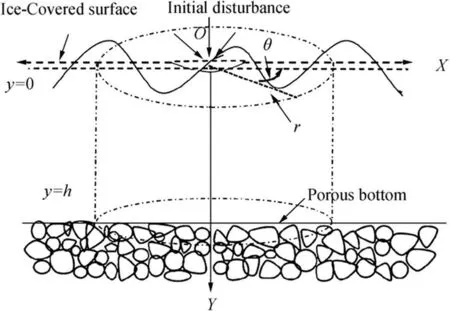
Figure 1 Sketch of physical model

2 Mathematical Formulation: Formulation of Initial Value Problem

We consider a cylindrical coordinate system (r,θ,y) in which they-axis is taken vertically downwards into the fluid region.The upper surface of the ocean is covered with a thin layer of ice modeled as a very thin elastic sheet having a uniform surface densityρ, whereis a constant having the dimension of length. Ocean fluid is considered an inviscid, incompressible,and homogeneous liquid of volume densityρ. Also, the bottom of the ocean is composed of some specific kind of porous materials which are characterized by a real parameterGhaving dimension inverse of length. The sketch of the physical model is shown in Figure 1. Wave motion is created due to a sudden initial axisymmetric disturbance at the ice-covered surface.

Since the motion starts from rest, it is irrotational and can be described by a velocity potentialφ(r,y,t), which satisfies Laplace’s equation.

whereGis the porosity parameter.

The kinematic condition arises due to the assumption of no cavitation between the ice and water. So, the condition gives

The initial conditions at ice-covered surface are

as the initial disturbance is axially symmetric depression or impulse at the ice-covered surface andζ′(r),F′(r) denote the nondimensional form of initial axially symmetric depression, impulse, respectively.

3 Method of Solution: Laplace and Hankel Transform Techniques

We use Laplace and Hankel transform technique to solve the above initial value problem. Now, let us define Laplace transform ofφ(r,y,t) in timetas

3.1 Case A (Gh<1)

WhenGh<1, the graphical behavior of,c2is shown in Figure 2. From the figure it is observed thatc2behaves well againstkfor small values of porosity parameter which may further indicate for small porosity parameter, the size of the pores in the sea bed is small.

There is a rootk=λand from graphical viewc2can be written as

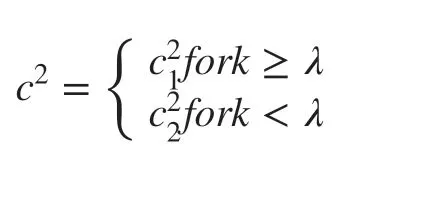
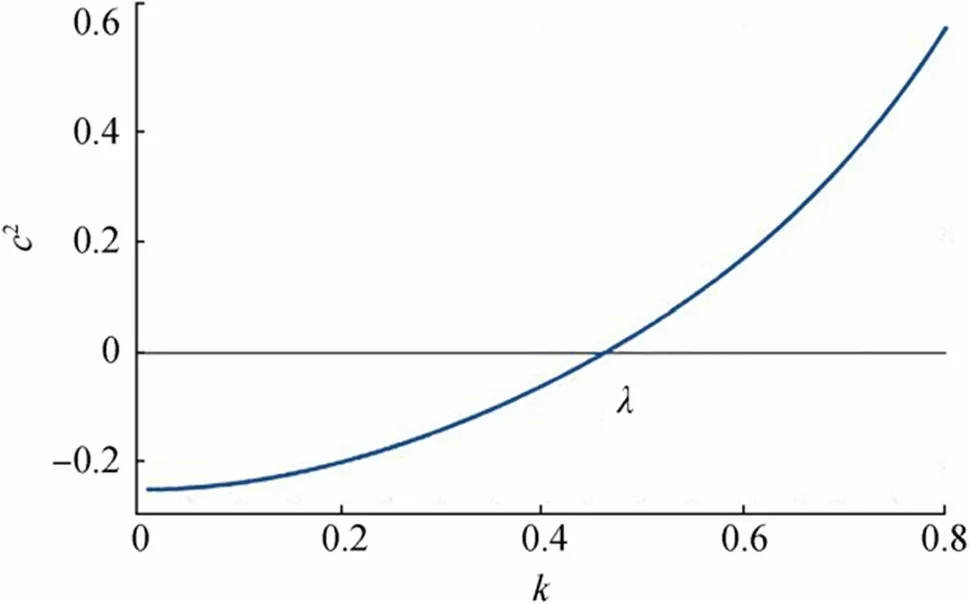
Figure 2 Graphical view of c2 for Gh=0.2,D=1.2,=0.01

So, taking Laplace inversions, we find the depression of the ice-covered surface in case of initial axially symmetric depression is obtained in the form

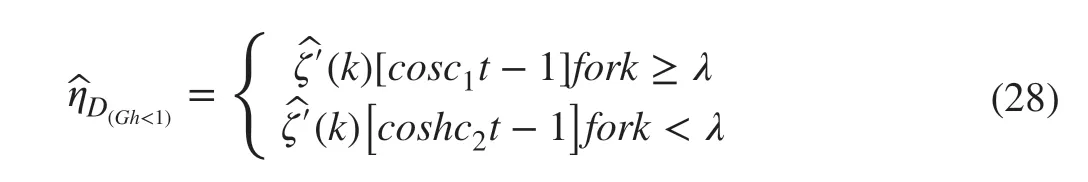
and similarly in case of initial axially symmetric depression is obtained in the form

Figure 3 Graphical view of c2 for Gh=1.2,D=1.2=0.01

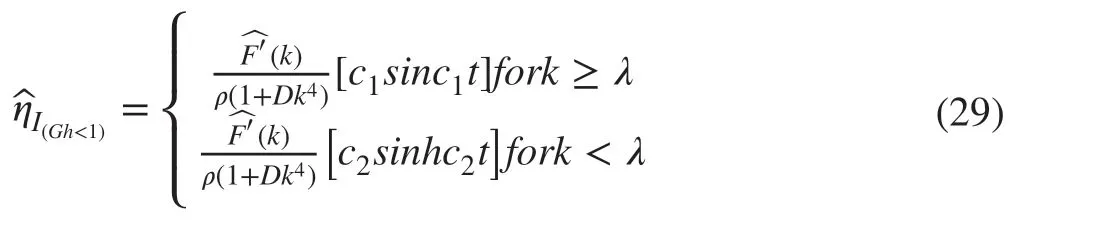
Finally, taking inverse Hankel to transform the form of ice-covered surface depression in case of initial axially symmetric depression or impulse forGh<1 are given by

3.2 Case B (Gh ≥1)

WhenGh≥1, the graphical behavior ofc2is shown in Figure 3.The denominator ofc2has a root ofk=λ1and numerator ofc2and has a rootk=λ2. From the figure, it is observed thatc2has a singularity in the domain for a larger value of porosity parameter, which may further indicate that for large porosity parameter the size of the pores in the sea bed is increasing slidely.

So, from graphical viewc2can be written as

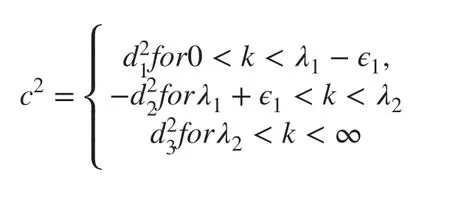
whereis an arbitrary small positive real number.

So, taking Laplace inversions using the Cauchy principal value of integrals, we find the depression of the ice-covered surface in case of initial axially symmetric depression is obtained in the form

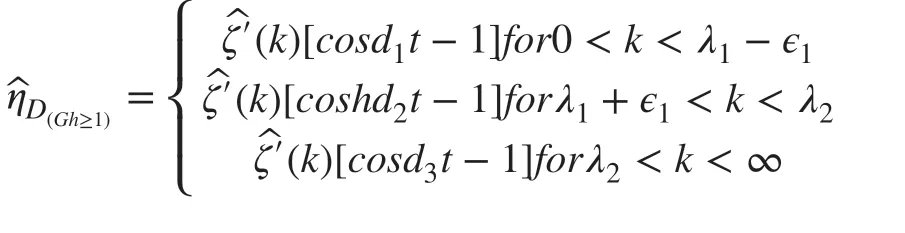
and similarly in case of initial axially symmetric depression is obtained in the form

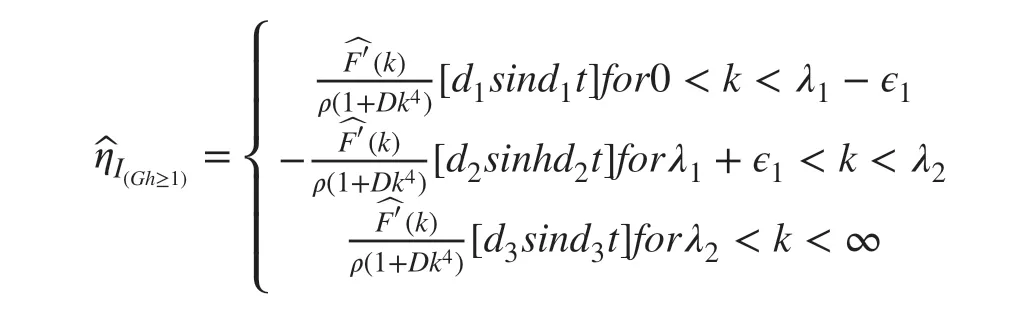
Finally, taking inverse Hankel to transform the form of ice-covered surface depression in case of initial axially symmetric depression or impulse forGh≥1 are given by

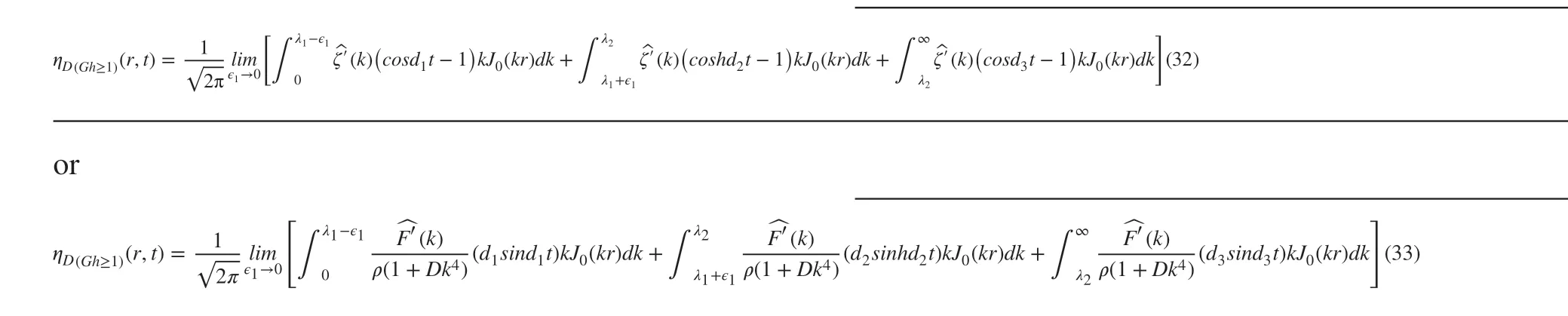
4 Asymptotic Expansion of Initial Depression of the Ice‑covered Surface:Stationary Phase Method

4.1 Case A (Gh<1)

We use the integral representation ofJ0(kr) as

Putting the approximation ofJ0(kr) on Eq. (30) we have

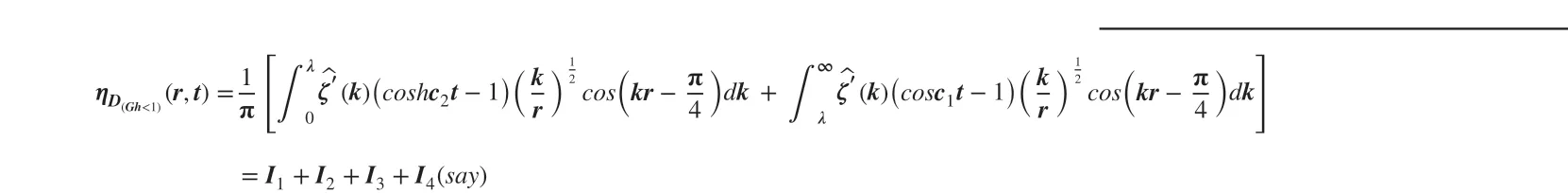
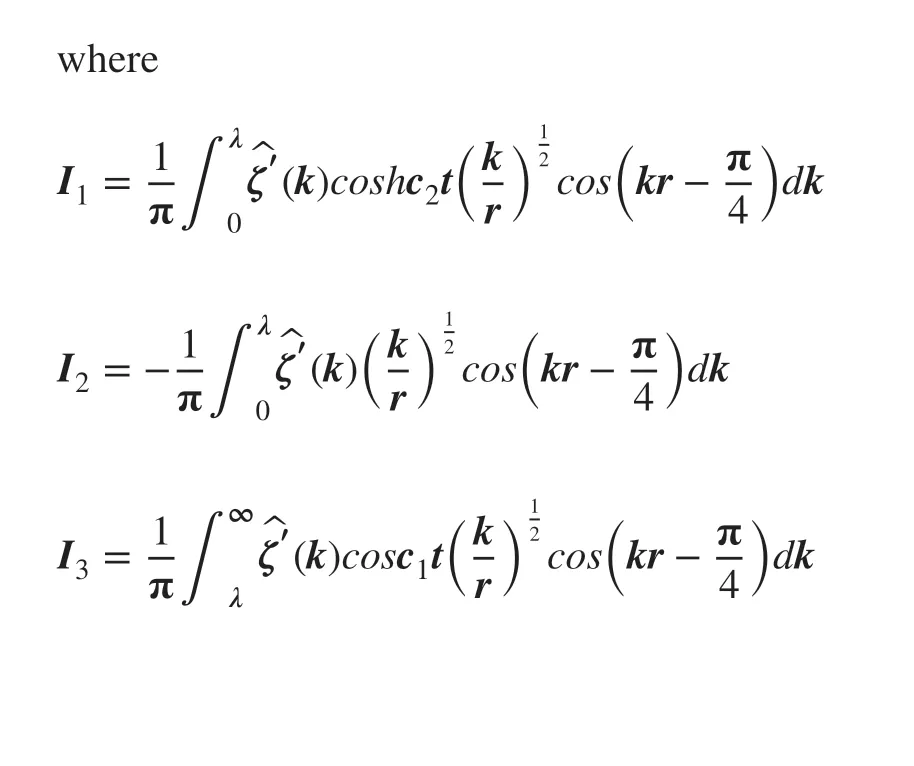
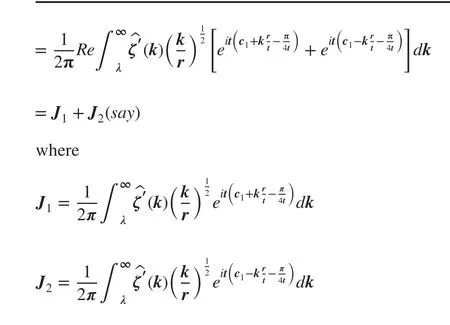
Now,J1does not contribute toI3as the phase function has no stationary point in the range of the integration andJ2can be written in the form of

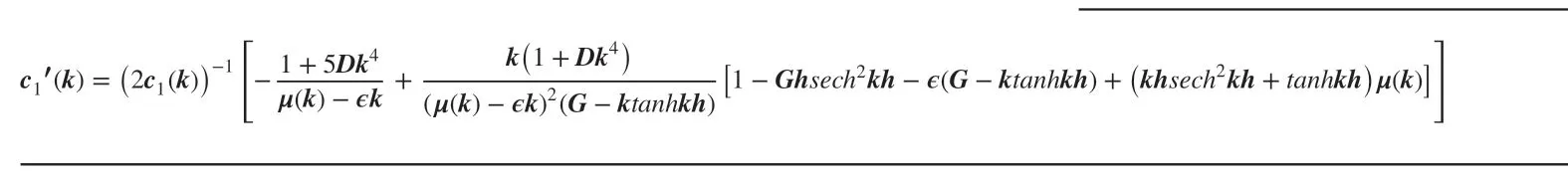
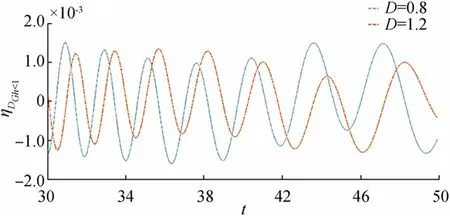
Figure 4 Wave motion due to initial depression for fixed distancer=150 and=0.01,Gh=0.5

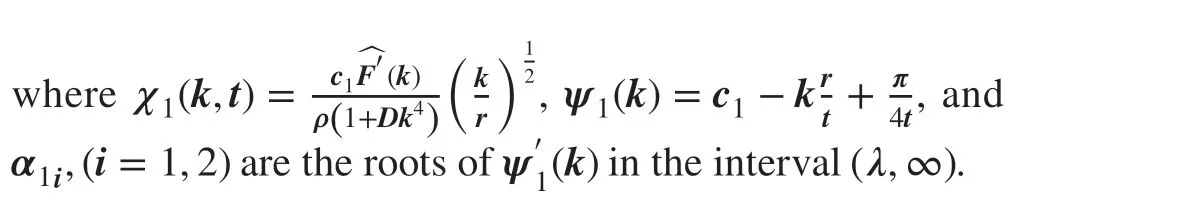
4.2 Case B (Gh ≥1)

ForGh≥1 using the approximations ofJ0(kr) the integral representation ofη(r,t) in case of initial axially symmetric depression is given by

Using the method of stationary phase to these integrals, the asymptotic form of the ice-covered surface depression, in case of axially symmetric impulse forGh≥1 is given by

4.3 Justification of the Method of Stationary Phase

We now prove how the integralsI1,I2,I4have no contributions to the ice-cover surface depression. Consider the integral

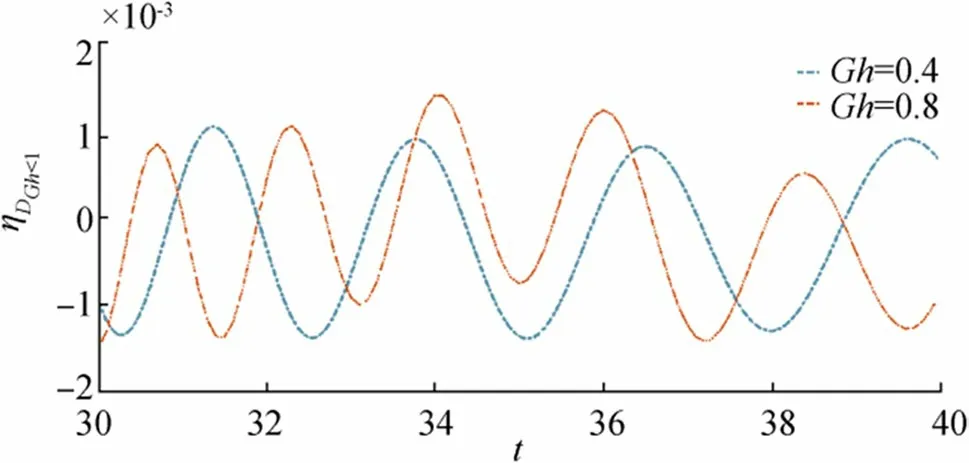
Figure 5 Wave motion due to initial depression for fixed distance r=150 and=0.01,D=1.2

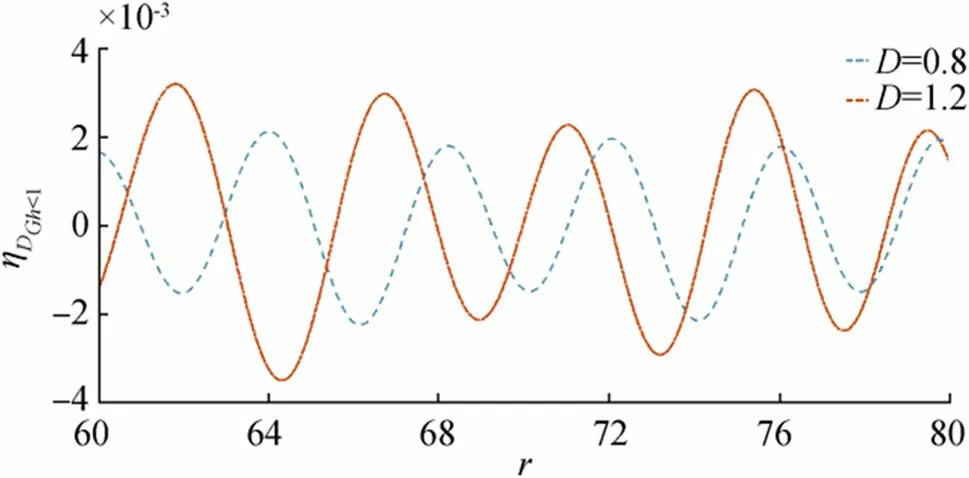
Figure 6 Wave motion due to initial depression for fixed time t=20 and =0.01,Gh=0.5

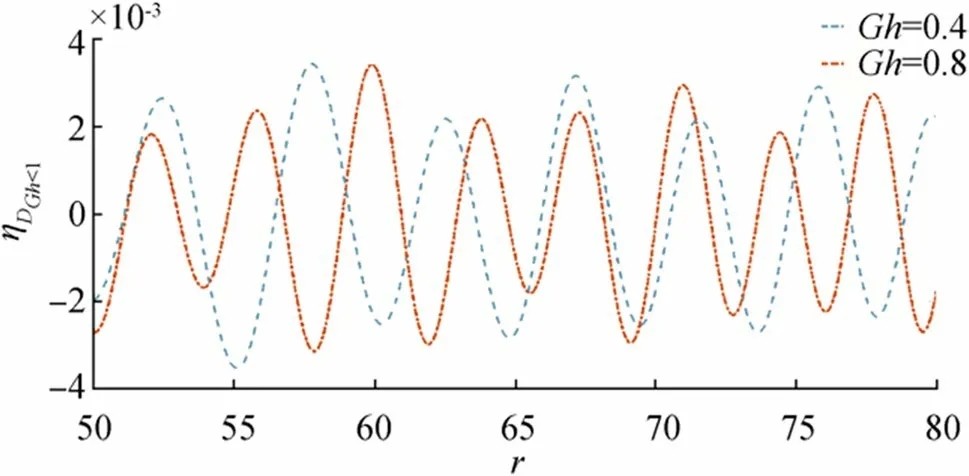
Figure 7 Wave motion due to initial depression for fixed time t=10 and =0.01,D=1.2

5 Numerical Results: Far‑Field Behavior of Wave Amplitude

In this section, to view the far-field behavior of the generation of surface wave in the presence of ice cover and porous bottom, the nondimensional asymptotic form ofη(r,t) is depicted graphically againstrfor fixedtand againsttfor fixedrin some figures for different values of porosity parameter and ice-cover parameters.

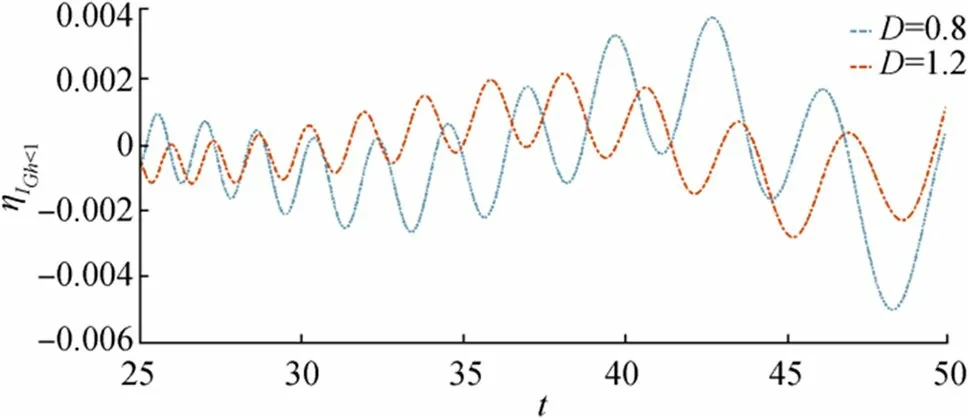
Figure 8 Wave motion due to initial impulse for fixed distance r=150 and =0.01,Gh=0.5

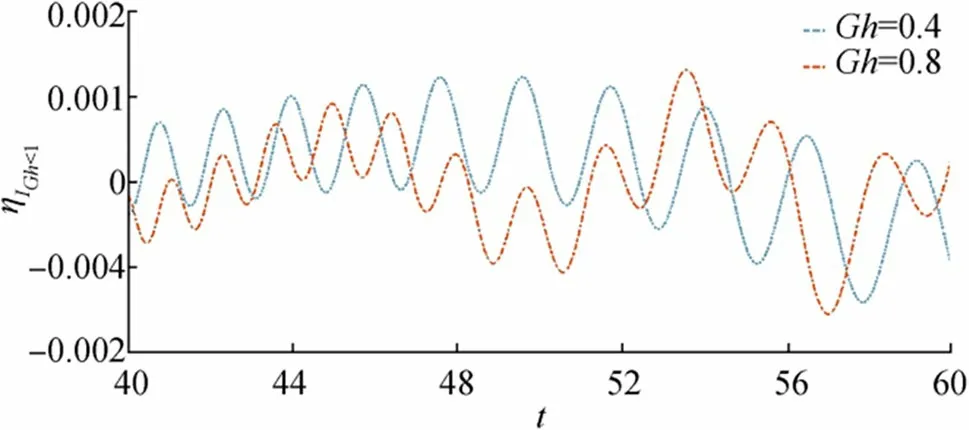
Figure 9 Wave motion due to initial impulse for fixed distance r=180 and =0.01,D=1.2

5.1 Case A (Gh<1)

5.1.1 Initial Depression

In Figure 4,ηDGh<1is displayed againsttfor different values of the ice-cover parameterDand fixedr,,Gh<1.From Figure 4 it is observed that asDincreases amplitude of ice-covered surface depression decreases from which it can be concluded that as the flexural rigidity of the ice sheet increases it can offer more resistance to the surface waves so that the oscillatory nature and amplitude of waves reduces.In Figure 5,ηDGh<1is displayed againsttfor different value of porosity parameterGand fixedr,,D.

From Figure 5, it is observed that near the time ranget=34 to 36 amplitude ofηis quite larger for large porosity parameter compared to other, although in the other regions amplitudes of both waves are nearly same.

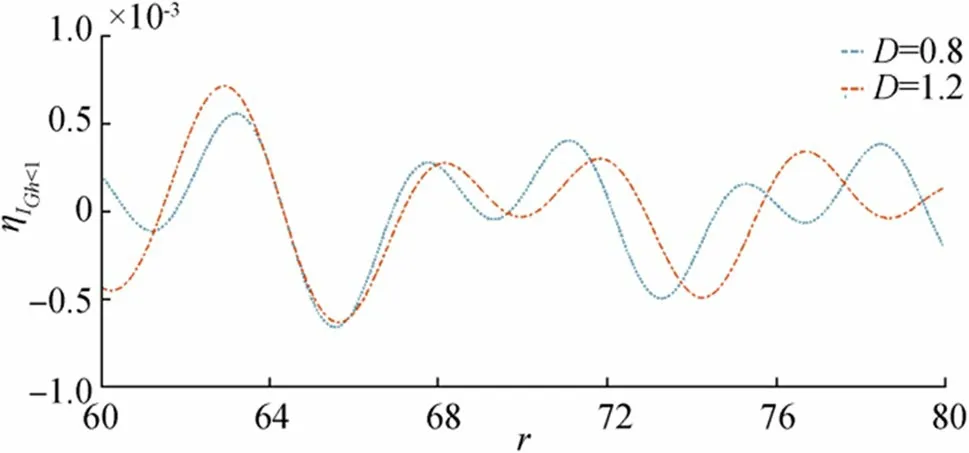
Figure 10 Wave motion due to initial impulse for fixed time t=15 and =0.01,Gh=0.5

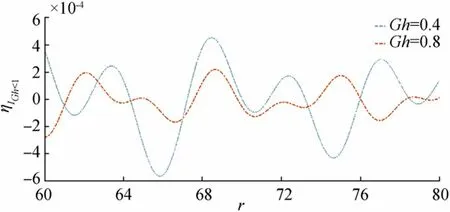
Figure 11 Wave motion due to initial impulse for fixed time t=15 and =0.01,D=1.2

In Figure 6, wave motion has been shown against distance due to initial depression for fixedt,,Ghand different values of the ice-cover parameter. Here the increase in the flexural rigidity of the ice sheet increases the amplitude of the wave motion slightly. Figure 7 shows wave motion against distance due to initial depression for fixedt,,Dand different values of porosity parameter less than 1. From this figure,it can be noted that nearr=60 amplitude wave is larger compared to the other regions for both the cases of porosity parameter.

5.1.2 Initial Impulse

In thies case, we consider initial axially symmetric impulseF′(r) as Dirac delta function or unit impulse function which is applied at a distancerfrom the origin for an infinitesimal interval of time. Figures 8, 9, 10, and 11 have shown the behavior ofηIGh<1due to initial impulse for different parametric values.

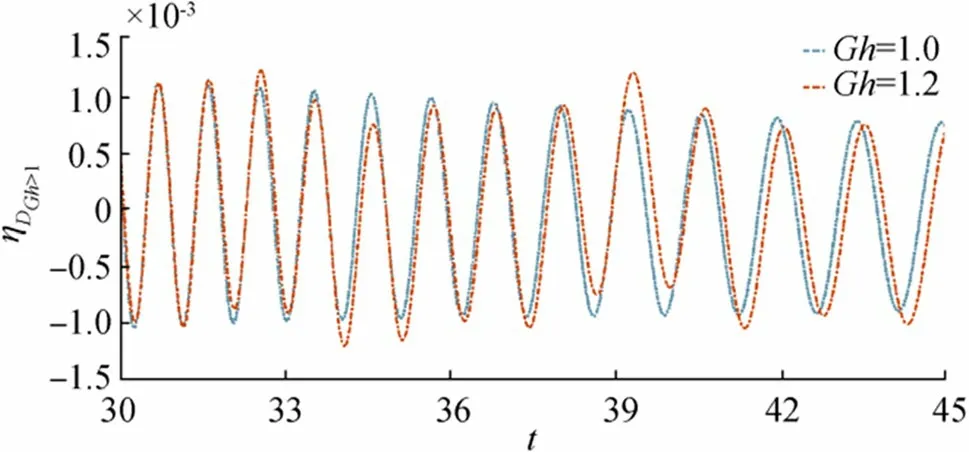
Figure 12 Wave motion due to initial depression for fixed distance r=120 and =0.01,D=1.2

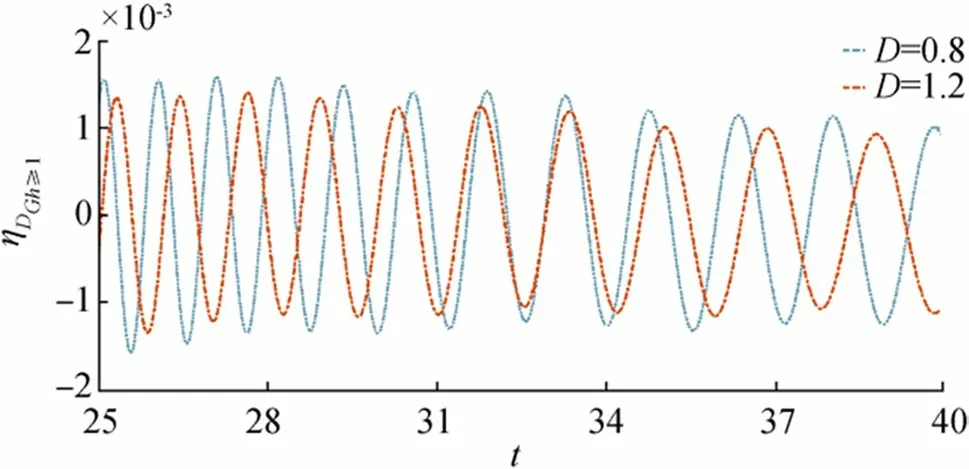
Figure 13 Wave motion due to initial depression for fixed distance r=120 and =0.01,Gh=1.2

In Figure 8,ηIGh<1is plotted againsttfor fixedr,,Ghand different values of the ice-cover parameter. The amplitude ofηIGh<1increases as time increases and as flexural rigidity of the ice sheet increases amplitude of the surface wave decreases. Wave motion due to initial impulse for fixedr,,Dis shown in Figure 9. From this figure, it is observed that surface waves show a highly oscillatory nature in this case.

In Figure 10,ηIGh<1is plotted againstrfor fixedt,,Ghand in Figure 11,ηIGh<1is plotted againstrfor fixedt,,D.From Figure 10, it is observed that the nature of surface wave is not much differing for two flexural rigidity parameters, but in the case of Figure 11, as the porosity parameter increases the amplitude of wave decreases.

5.2 Case B (Gh ≥1)

5.2.1 Initial Depression

Figures 12, 13, 14, and 15 are drawn for initial depression in case of higher porosity parameter i.e.,Gh≥1. Figure 12 shows behavior ofηIGh≥1for fixedr,,Dand Figure 13 shows behavior ofηIGh≥1for fixedr,,Gh. From Figure 12,it is observed that as bottom porosity increases the surface waves move almost the same manner and show a very slide difference between amplitude but in the case of Figure 13 wave amplitude decreases significantly asDincreases. Figures 14 and 15 show generation ofηIGh≥1againstrfor fixedt,andD,Gh, respectively.

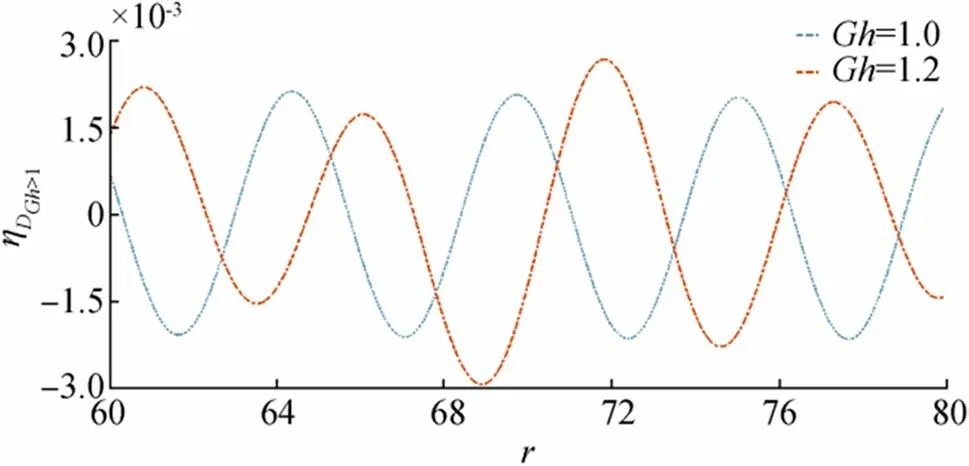
Figure 14 Wave motion due to initial depression for fixed time t=20 and =0.01,D=1.2

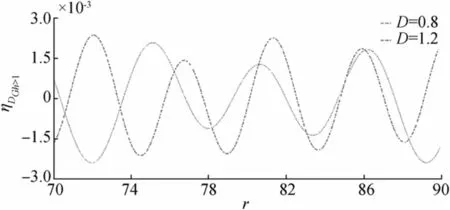
Figure 15 Wave motion due to initial depression for fixed time t=20 and =0.01,Gh=1.2

5.2.2 Initial Impulse

Figure 16 to Figure 19 show the behavior ofηIGh≥1due to initial impulse for different parametric values. In Figure 16,ηIGh≥1is plotted againsttfor fixedr,,Dand different values of porosity parameter. Amplitude ofηIGh≥1increases as time increases and variation ofηIGh≥1almost coincides for the two casesGh=1,1.2.

Wave motion due to initial impulse for fixedr,,Ghis shown in Figure 17. From this figure, it is observed that asDincreases amplitude of wave motion, it reduces considerably. Similar behavior observed in Figures 18 and 19, in whichηIGh≥1plotted againstrfor fixedt,,Dandr,,Gh, respectively.

5.3 Validation through comparison with previous results

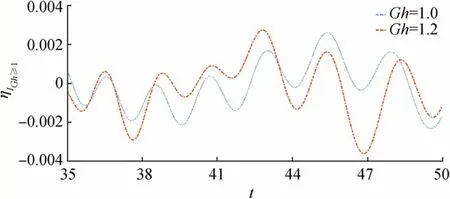
Figure 16 Wave motion due to initial impulse for fixed distance r=180 and =0.01,D=1.2

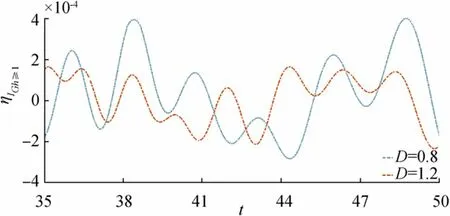
Figure 17 Wave motion due to initial impulse for fixed distance r=180 and =0.01,Gh=1.2

In this section, we compared our result with the existing result of Maiti and Mandal (2005), taking the depth of fluid region,his large and porosity parameterGis quite small.In Figures 20 and 21, graphical behavior of free surface depressionηis shown in case of initial axially symmetric depression and impulse (taken as Dirac Delta function). In both, the figures dotted curve shows the nature ofηagainsttfor the existing result of Maiti and Mandal (2005) for fixedr=60,=0.01,D=0.5 and the thick curve shows behavior ofηfor our result, againsttfor fixedr=60,=0.01,D=0.5 and takingh=50,G=0.00001. In both figures, these two curves (dotted and thick lines) represent the nature of wave motion match quite well with each other.

Here, we consider another comparison between the present result and Kundu and Mandal’s (2019) result. Kundu and Mandal (2019) considered the generation problem by an initial axisymmetric surface disturbance in presence of porous bottom. In Figure 22 we have drawn both the results side by side, which shows the clear effect of ice cover onηcurve for initial depression. The curves are drawn for fixed values oft=20,=0.01,Gh=0.5. The dotted line represents Kundu and Mandal’s (2019) data with no ice cover and the thick line shows the present result. The present result is drawn considering two different values ofD=0.5 and 1.2. From the figure, it is quite clear that the presence of ice cover shows more oscillation and amplitude in the wave depression curve.

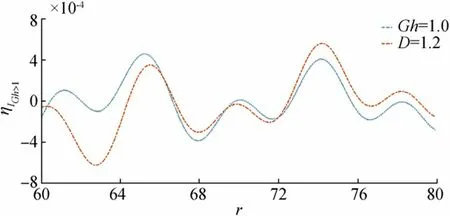
Figure 18 Wave motion due to initial impulse for fixed time t=15 and =0.01,D=1.2

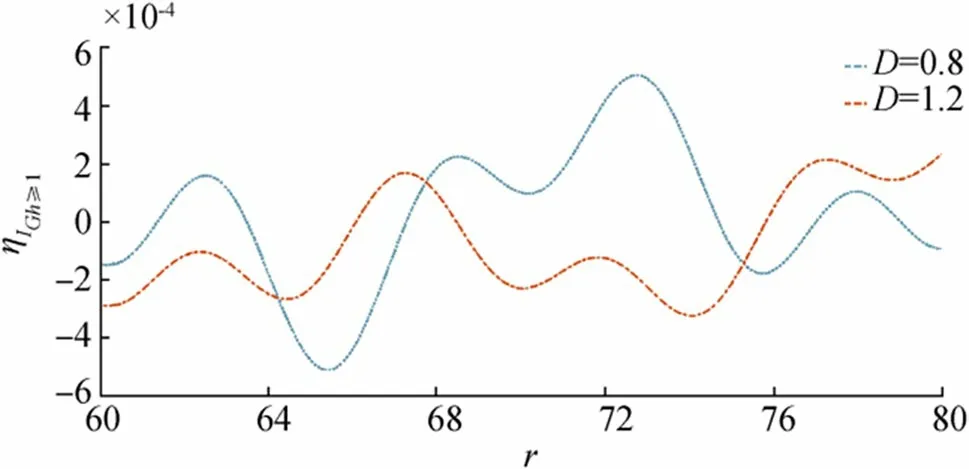
Figure 19 Wave motion due to initial impulse for fixed time t=15 and =0.01,Gh=1.2

For a clearer comparison, we have tabulated the present data and Maiti and Mandal (2005)’s data side by side in Table 1, for fixedr=60,=0.01,D=0.5.

Maiti and Mandal discussed the problem in infinitely deep water. In the present calculation, we consider very small values ofG=0.00001 and very large water depthh=100. From the table, it is clear that the present result is matched with Maiti and Mandal’s (2005) result up to 4 decimal places. This implies another check on the correctness of the results obtained here.

From these three figures and tabular values of ice-covered surface depression, it is observed that our result matches well with the existing result of the literature. This provides the desired check on the correctness of the method presented here.

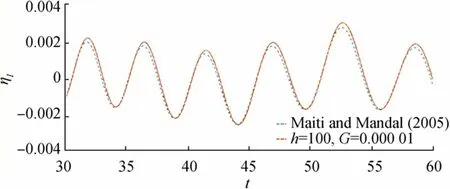
Figure 21 Wave motion due to initial depression for fixed distance r=60 and =0.01,D=0.5

5.4 Phase velocity, Group Velocity, and Wavelength

We consider the case of simple harmonic motion in time with angular frequencyσto understand the behavior of surface waves in presence of ice-cover and porous bottom. The dispersion relation for surface wave in presence of porous bottom and ice-cover at the free surface can be written as

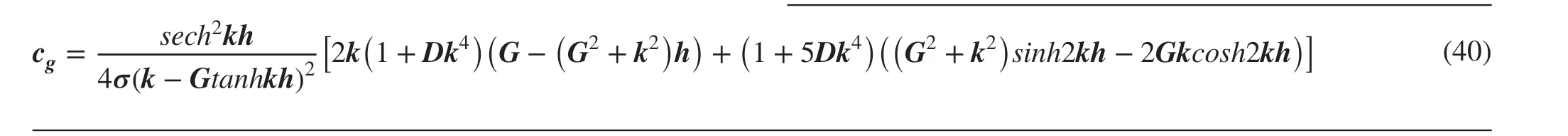
Figures 23 and 24 demonstrate phase velocity (c)against wave number, and Figures 25 and 26 demonstrate the variation of group velocity (cg) against wave number.Figures 23 and 25 show the variation of phase velocity and group velocity, respectively, for a fixed value of flexural rigidity coefficientD=1.2 and taking different values ofGh=0.4,0.8,and1.2. Increasing values of porosity parameter increase bothcandcgand it is clearly seen from the figures that for each value of porosity parameter,cg>cwith varying wave number.

Table 1 Depression of ice cover for r=60,=0.01,D=0.5

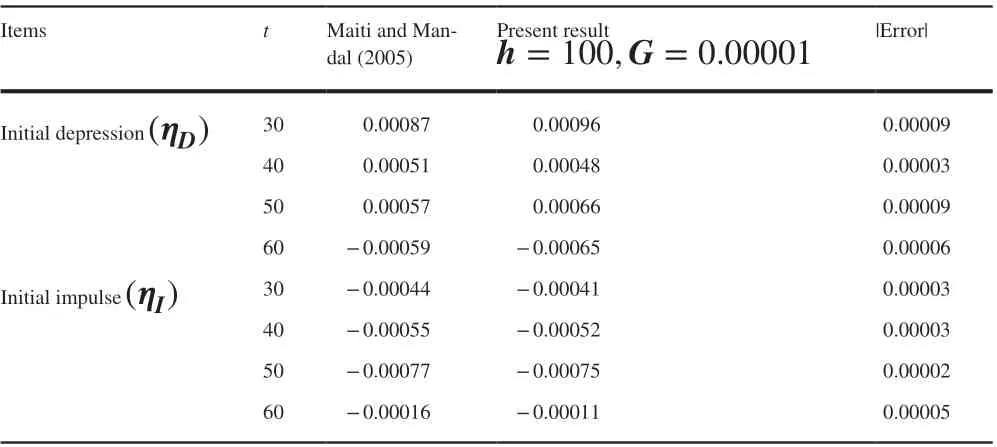
Table 1 Depression of ice cover for r=60,=0.01,D=0.5

ItemstMaiti and Mandal (2005)Present result h=100,G=0.00001|Error|Initial depression (ηD)300.000870.000960.00009 400.000510.000480.00003 500.000570.000660.00009 60−0.00059−0.000650.00006 Initial impulse (ηI)30−0.00044−0.000410.0000340−0.00055−0.000520.00003 50−0.00077−0.000750.00002 60−0.00016−0.000110.00005

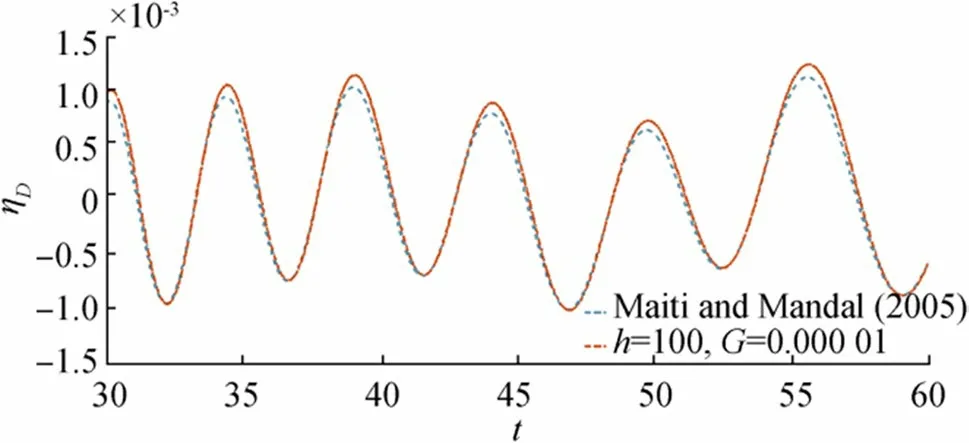
Figure 20 Wave motion due to initial impulse for fixed distance r=60 and =0.01,D=0.5

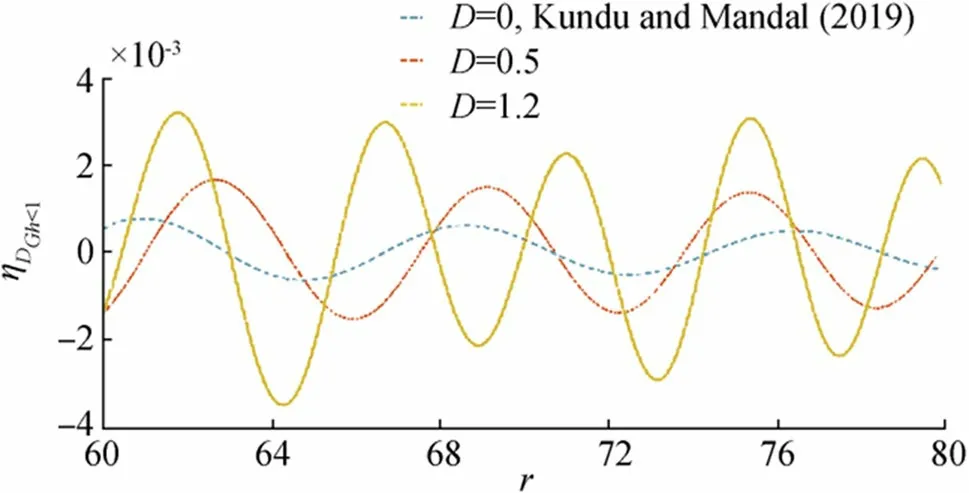
Figure 22 Wave motion due to initial depression for fixed time t=20and =0.01,Gh=0.5

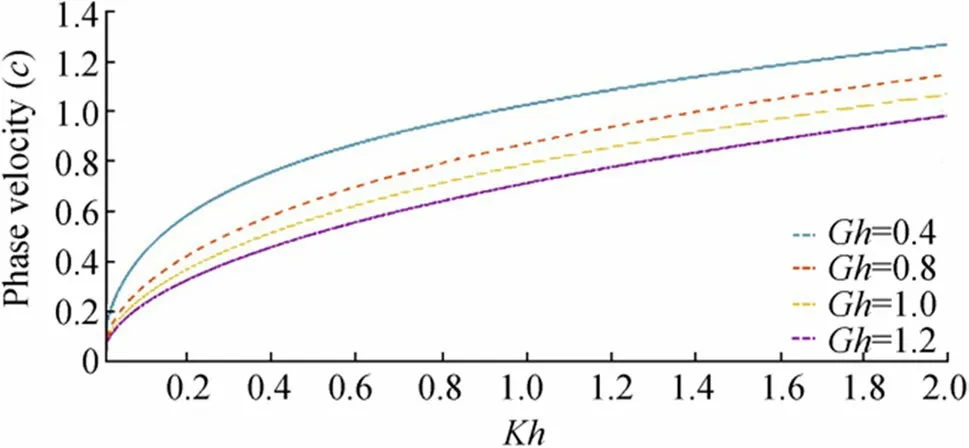
Figure 23 Phase velocity (c) against frequency Kh for fixed D=1.2

From Figure 25, it can be seen thatcgattains its maximum value for a very small wave number and eachcgcurve decreases with large values of wavenumber.

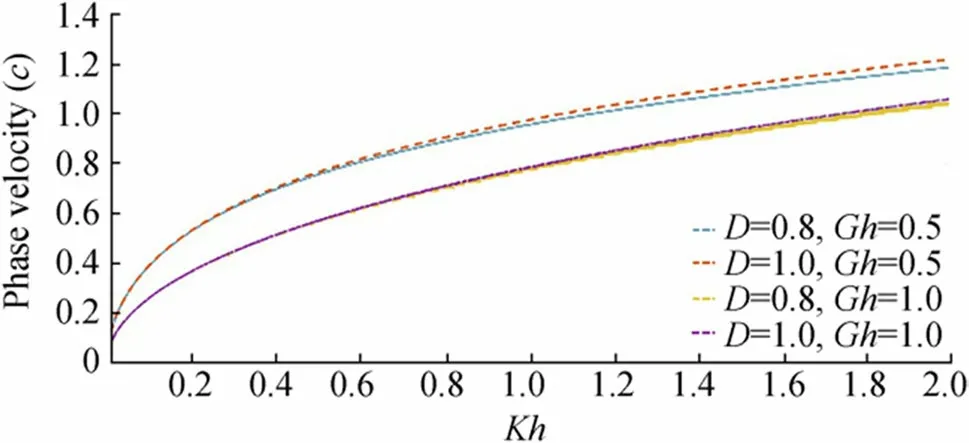
Figure 24 Phase velocity (c) against frequency Kh for fixed Gh=0.5and Gh=1

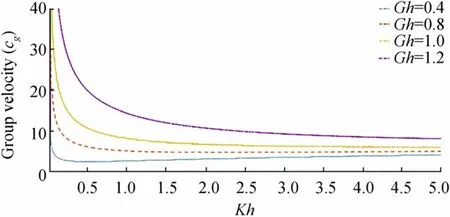
Figure 25 Group velocity (cg) against Kh for fixed D=1.2

Figures 24 and 26 depict the phase velocity and group velocity, respectively, against wave number for fixed values ofGh=0.5 and 1 and different values of flexural rigidity coefficientD=0.8,1.2. It is seen that with increasing values of rigidity coefficient magnitude of phase velocity and group velocity both increase. Comparing Figures 24 and 26, it can be observed that with each fixed value of rigidity parameter alwayscg>c. Figure 24 depicts that for small values of wave number; the phase velocity curves corresponding to different values ofDare shown nearly the same behavior whereas a more prominent increasing nature of the curves is shown for large wavenumbers. At the zero wave number,phase velocity attains minimum value, nearly zero; hence progressive wave does not propagate there.

From Figure 26, it is clear that varying porosity parameterscginitially decrease. It has attained a minimum value forKh<1 but with large values of wavenumber, it again increases.

6 Conclusions

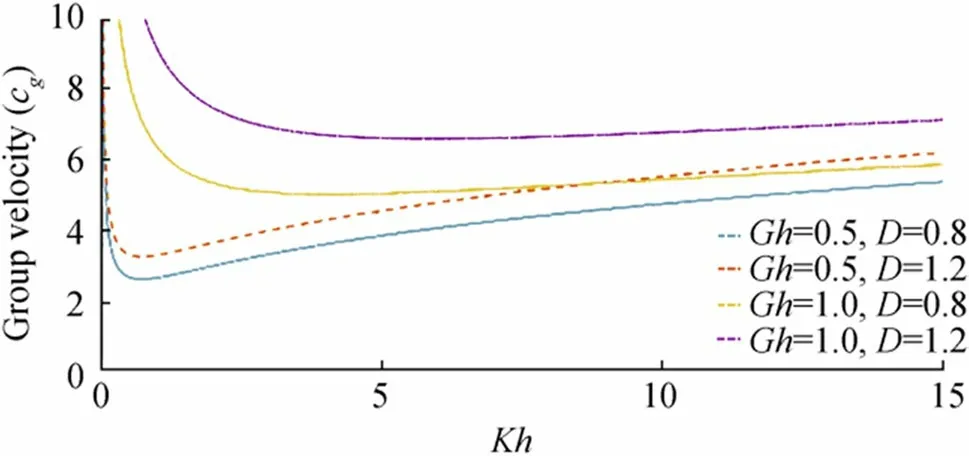
Figure 26 Group velocity (cg) against Kh for fixed Gh=0.5 and Gh=1

In the present study, wave generation due to an initial axisymmetric disturbance at the surface of an ice-covered ocean with a porous bed is studied using Laplace and Hankel transform method under the assumption of linear water wave theory. The integral representation of the upper surface elevation is approximated by using the stationary phase method. The form of ice-covered surface depression is depicted graphically in a number of figures against time for some fixed distances from the shoreline and against the distances from the shoreline for some fixed values of time for two types of initial axially symmetric disturbances. The figures are drawn with either different values of the rigidity coefficient of the thin elastic ice sheet or different values of the porosity parameter of the sea bed. Here we consider the porosity parameter real. It is observed from the figures that as the flexural rigidity of the thin ice sheet increases,the plate can resist the generation of the surface wave so that the oscillatory nature of the wave reduced significantly.Further ocean waves generating in the ice field are observed to decrease in amplitude, and this observed reduction is preferably due to the presence of both ice sheet and bottom porosity. In the presence of a porous bed and ice cover, the phase velocity and group velocity of the gravity waves are depicted graphically in some figures for time-harmonic motion.