高温下不同受火面对开洞剪力墙温度场的影响

王中强，周铮

（长沙理工大学 土木工程学院，湖南长沙 410114）

0 引言

在我国经济飞速发展和商业需求不断扩增的背景下，高层与超高层结构应用愈加广泛，常用于高层结构中的剪力墙以及筒体结构也与实际工程的联系越来越紧密。 而在实际建筑工程中，因设计功能的改变和房屋装修的需要，常常会碰到对剪力墙开洞的情况。剪力墙作为剪力墙结构、框架-剪力墙结构以及核心筒结构中的主要抗侧力构件，对其开设洞口，不仅会削弱剪力墙自身抗侧移能力，而且会影响原有结构性能。

目前，全国各地的火灾发生频率越来越高，且随着建筑物高度的增加，火灾造成的危害也更加严重。 火灾不仅会严重损害人们的生命财产，而且会对建筑结构造成不同程度的损伤，因此，对火灾后的结构使用评估尤为重要。 现阶段人们对于常温下的剪力墙力学性能进行了大量的实验及研究，但对剪力墙受火以及受火后力学性能的损伤研究较少。

本文以某实际结构中一片一字型开洞剪力墙为研究对象，采用Abaqus 有限元分析软件， 在温度场理论分析的基础上建立了开洞剪力墙模型， 并分别考虑了单面受火和双面受火的情况，通过数值计算对比受火面对开洞剪力墙温度场的影响。 分析结果可为进一步进行高温下剪力墙力学性能分析与火灾后修复加固提供参考。

1 温度场分析理论基础

1.1 计算假设

本文在对受热混凝土剪力墙温度场进行分析时，采取如下假设：

（1） 混凝土各个方向均质、同性，且内部不产生热量；

（2） 忽略混凝土内部水的迁移、蒸发以及质量密度改变的影响；

（3） 不考虑热能与机械能之间的转化耦合，即忽略材料应力、应变的机械作用转化涉及的小部分热量；

（4） 热传递时忽略钢筋影响。

1.2 高温下材料相关热工参数

（1） 质量密度

随着温度的升高，混凝土内部水分会因蒸发减少，导致混凝土质量密度有微弱减少。 本文对质量密度的变化采取文献[1]所用公式：

为简化计算，本文取为常数Pc(T)=2300 (kg/m3)

（2） 比热容

单位质量的混凝土在温度降低或者升高1℃所放出或吸收的热量即为混凝土的比热容。本文对混凝土的比热容采用文献[2]所用公式：

（3） 热传导率

热传导率又被称为导热系数，是指材料单位体积下，在单位时间和单位温度差异下传导的能量。本文对混凝土的导热系数采用文献[3]所述表达式：

（4） 热膨胀系数

随着温度的改变，物质体积会发生膨胀和收缩现象。 因此在研究混凝土受热时，本文对混凝土的热膨胀系数采用文献[4]所用公式：

1.3 边界条件

分析剪力墙受火这个物理过程时， 除了温度控制方程外，还需要给定初始条件和边界条件。 因此，本文给定初始时刻的温度分布为：

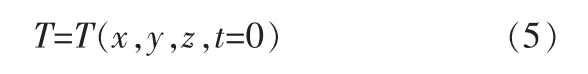
本文在温度场计算中，初始环境温度取20℃。 受火边界条件主要分为以下三类[5]：

（1） 第一类定解条件：已知构件表面的温度与时间的关系函数

（2） 第二类定解条件：已知受火面的表面热流密度大小

（3） 第三类定解条件：已知热辐射和受火面边界对流条件

本剪力墙结构模型构件的受火面采用第三类定解条件，与受火面接触的环境温度变化情况取ISO-834 标准升温曲线；背火面的初始温度不随时间改变，因此取为第一类边界条件，大小值取常温（即20℃）。混凝土表面和大气的热交换系数大小主要取决于空气流动的快慢，系数数值在20～80（W/m℃）区间内。对于本文采用的混凝土剪力墙模型，要分别考虑单双面受火。 由于空气流动速度快，受火面取 h=25（W/m℃），背火面取 h=15（W/m℃）[6]。 而对于热辐射传递，剪力墙模型受火侧的热辐射系数取0.8，背火侧取0.1。

1.4 标准升温曲线

ISO-834 标准升温曲线是在大量建筑火灾的基础上分析得到的，对火灾模拟和火灾试验有重要的参考意义，其表达公式如下：

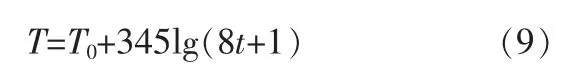
其中，T 为随受火时间变化的温度；T0为环境温度；t 为受火时间。 在Abqus 中根据标准升温曲线建立的振幅曲线如图1 所示。

图1 根据标准升温曲线建立的振幅曲线

2 有限元模型建立及结果分析

2.1 模型建立

本文建立的一字型剪力墙模型取自某高层结构中， 剪力墙的高度为 3000mm， 墙肢的厚度为 200mm， 剪力墙肢长为500mm，且设有1000mm 宽的门洞，连梁高度为 400mm，混凝土等级采用C30。受火方式分别考虑单侧和双侧受火， 受火面采用国际标准升温曲线进行升温， 背火面采用标准环境温度20℃。 具体有限元模型详见图2。

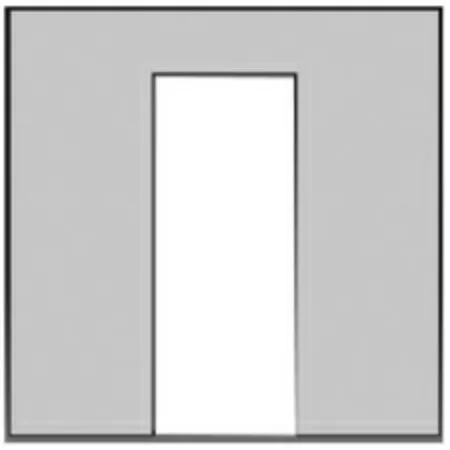
图2 剪力墙模型正面图

模型建立时， 传热单元选用混凝土 DC3D8 八节点六面体[7]。 进行有限元分析时，划分模型网格越精确， 分析结果越接近实际。 但是网格划分越密，计算效率越低，因此，本文在综合考虑精密度、计算效率等因素后， 选取10mm 的网格尺寸进行有限元分析，网格划分见图3。

图3 剪力墙模型网格划分图

2.2 温度场结果分析

2.2.1 双面受火温度场分析

双侧受火60min 后，剪力墙连梁跨中截面温度分布云图如图4 所示，受火120min 后的连梁截面温度分布云图如图5 所示。 为了进一步分析截面节点高度对温度的影响，本文以连梁跨中截面节点为对象，分析温度分布情况，其温度与时间变化的关系曲线如图6 所示。

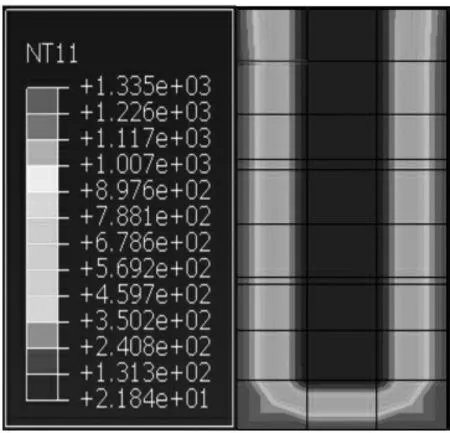
图4 60min 时连梁跨中截面温度分布云图

图5 120min 时连梁跨中截面温度分布云图

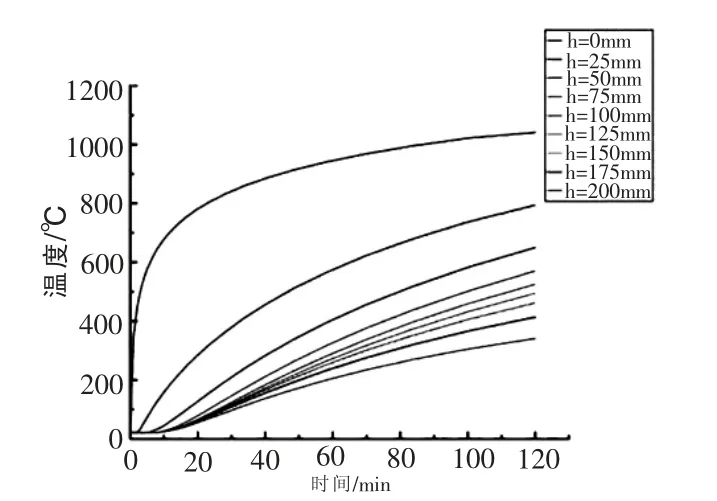
图6 剪力墙连梁处截面节点温度变化图

双面受火的剪力墙墙肢跨中截面在60min 时的截面温度分布云图如图7 所示，120min 时的截面温度分布云图如图8 所示。

图7 60min 时剪力墙竖向截面温度分布云图

图8 120min 时剪力墙肢竖向截面温度分布云图

2.2.2 单面受火温度场分析

单侧受火60min 后，剪力墙连梁跨中截面的温度分布云图如图9 所示，受火120min 时的截面温度分布云图如图10 所示。 连梁跨中截面节点高度对温度的影响与双面受火情况基本相同，因此不再重复。

图9 60min 时连梁跨中截面温度分布云图

图10 120min 时连梁跨中截面温度分布云图

单面受火的剪力墙肢跨中截面在60min 时的截面温度分布云图如图11 所示，120min 时的截面温度场如图12 所示。

图11 60min 时剪力墙肢竖向截面温度分布云图

图12 120min时剪力墙肢竖向截面温度分布云图

2.2.3 单面受火与双面受火对比分析

相同的热工条件下对有限元模型升温120min 后， 单侧受火情况下，剪力墙肢内部温度差异较大，且受火面与背火面热度差异较为明显；双侧受火情况下，剪力墙肢内部温度差异比较小，节点与受火面的距离大小与节点温度间关系密切。 对比两种受火方式的剪力墙肢中心测点温度，发现单面受火下的温度为144℃，双面受火下的温度为165℃，双面受火温度高于单面受火11℃。而在连梁处，双面受火下连梁跨中截面的中心测点温度相比于单面受火情况下，要高出24℃左右。可见在双面受火的情况下，剪力墙肢和连梁中心区域温度比单面受火更高，且两种受火情况下连梁跨中截面温度比剪力墙肢跨中截面温度差异更大。

3 结论

本文给定了温度场的计算假设，考虑了热传递的三种基本方式， 应用有限元分析软件Abaqus 对开洞剪力墙进行了温度场模拟分析，并对单面受火和双面受火两种情况进行对比，根据温度场分布情况，得出结论如下：

（1） 剪力墙在火灾作用下，墙肢内各个节点升温曲线略微滞后于标准升温曲线，但总体变化趋势与升温曲线接近。 墙肢内节点与受火面垂直距离相同时，温度基本相同。 但离受火面越近，温度梯度的差异越大。

（2） 其余条件相同，在受火时间分别取 60min 和 120min 的情况下，发现受火时间的增加，会使得墙肢截面温度梯度减小，说明受火条件对截面温度分布影响很大。

（3） 其余条件相同，取不同受火面的情况下，发现双面受火的剪力墙中心温度比单面受火的温度要高，且连梁跨中截面处的温度差异比墙肢中间的温度差异更大。