基于数据物理驱动的油藏调剖动态预测新方法
赵辉,刘邓,江厚顺,曹琳,2,张记刚,刘玉洋,王宁
1.长江大学石油工程学院,湖北 武汉 430100 2.中国科学院渗流流体力学研究所,河北 廊坊 065007 3.中国石油新疆油田分公司勘探开发研究院,新疆 克拉玛依 834000 4.海洋石油高效开发国家重点实验室,北京 100020
当前,水驱开发仍是我国大部分油田的主体开发方式,长时间开发导致注采矛盾突出,多级优势流场并存且难以识别[1-3]。目前,调剖堵水已成为注水开发中一类重要的工艺改造措施,调剖预测方法主要有矿场试验方法、统计学模型法和数值模拟法[4-6]。矿场试验法和统计学模型法主要依靠人工经验决策,没有结合地层连通认识,现场调剖堵水措施整体成功率低、见效差、失效快[7-10]。而针对调剖的数值模拟技术还不够成熟,对调剖动态的精确模拟预测比较困难,主要问题在于调剖剂渗流机理复杂,难以精细描述;数值求解困难,无法快速计算;同时,没有融合井间连通优势流道信息,很难进行精确模拟和方案优化,难以实现大规模应用[7-10]。
近年来,赵辉等[11-13]提出了一种新的数据物理驱动模型INSIM(Physics-based data-drivenmodel),不同于机器学习等驱动模型,其只需利用油水井生产数据和井位信息建模,其是在遵循物质平衡的条件下进行快速动态预测,并通过历史拟合反演井间传导率和连通体积等参数,定量表征井间连通关系。此后,一些学者在INSIM基础上开展了相关研究,建立了INSIM-FT[14]、INSIM-FT-3D[15]、INSIM-FPT[16]及聚合物驱窜聚动态预测[17]等模型。在INSIM模型基础上,笔者考虑多层油藏特点和调剖堵水作用机理,沿连通单元进行流动处理,建立了一种多层油藏调剖动态预测新方法,相比传统数模计算,该方法可提速上百倍,在满足计算精度要求下主要利用实际生产数据同步实现窜流通道识别和大规模调剖动态的模拟及优化。
1 多层INSIM模型
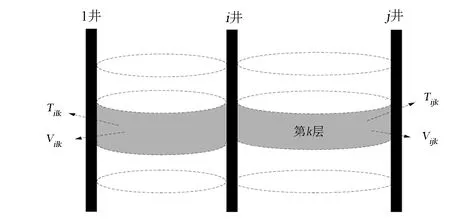
图1 连通单元体示意Fig.1 The schematic diagram of connected unit
依据INSIM模型建立方法[11-13],融合多层油藏连通信息特征,建立了一种多层INSIM模型,其基本思想是将油藏注采系统分层简化表征为一系列井与井之间由井间传导率(Tij)和连通体积(Vpij)组成的连通单元体(见图1)。其中,前者反映井间的平均渗流能力和优势传导方向,后者表征单元的物质基础,能够反映井间水驱控制范围和体积。以连通单元体为模拟对象基于物质平衡计算产出动态,再结合历史拟合反演模型连通参数。
对于i井,忽略毛管力及重力影响,建立物质平衡方程:
(1)
对式(1)进行隐式差分离散,设时间步长为Δt,得到差分方程:
(2)
(3)
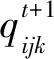
(4)
式(4)计算得到连通单元体内流量分布,以连通单元体为对象采用式(5)进行饱和度追踪计算[11]:
(5)
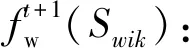
(6)
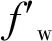
得到单井含水率后,可以进一步计算其他生产指标,如日产油量、日产水量、累计产油量等,即实现对油藏生产动态的快速预测。整个流动计算转换为一维流动处理,相比传统数值模拟速度可提高上百倍。
模型中各连通单元体的连通参数初值可依据井点物性和连井剖面信息如平均渗透率和有效厚度等进行计算[12]。同时,为了使模型计算结果与实际动态相符,通过引入计算机辅助历史拟合方法对井间传导率、连通体积等参数进行快速反演。主要采用SPSA算法[18],主要迭代公式为:
ml+1=ml-γF(ml)m=[…,Tij,Vpij,…]
(7)
式中:γ为迭代步长;F为随机扰动近似梯度;m为模型参数向量;l为步数。
2 调剖动态指标预测
应用多层INSIM模型获取井间连通信息后,考虑调剖作用机理建立调剖动态预测方法,其基本思想如下:基于历史拟合后的数据物理驱动模型计算注采井间的劈分系数及水井注水效率,优选注水效率较低的注水井作为调剖井;根据调剖井向周边连通单元体的劈分系数,计算注入堵剂后在各个连通单元体方向上堵剂的分配量;结合室内试验结果(如不同注入堵剂量下,渗流能力的下降关系),建立堵剂注入量与连通参数(如传导率)之间的关系,计算注入堵剂后的传导率,再代入物质平衡方程计算,即可实现调剖后的生产动态预测。
具体流程如下:
步1 注水劈分计算及调剖井优选。设j井为第k层的注水井,i井为与其相连的生产井,注水劈分系数定义为注水井的注入量到与其连通的生产井之间的液量分配比例,计算公式为:
(8)
注水效率定义为单位注水量能从周边生产井驱替的产油量,计算公式为:
(9)
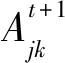
将计算得到的当前时刻所有注水井的注水效率进行排序,并与区块平均注水效率进行对比,将注水井分为高效井(注水效率高于区块平均注水效率)和低效井(注水效率低于区块平均注水效率);同时,考虑注水井注水量的大小,可优先选择效率低、注水量较大的井进行调剖,因其无效注水严重。
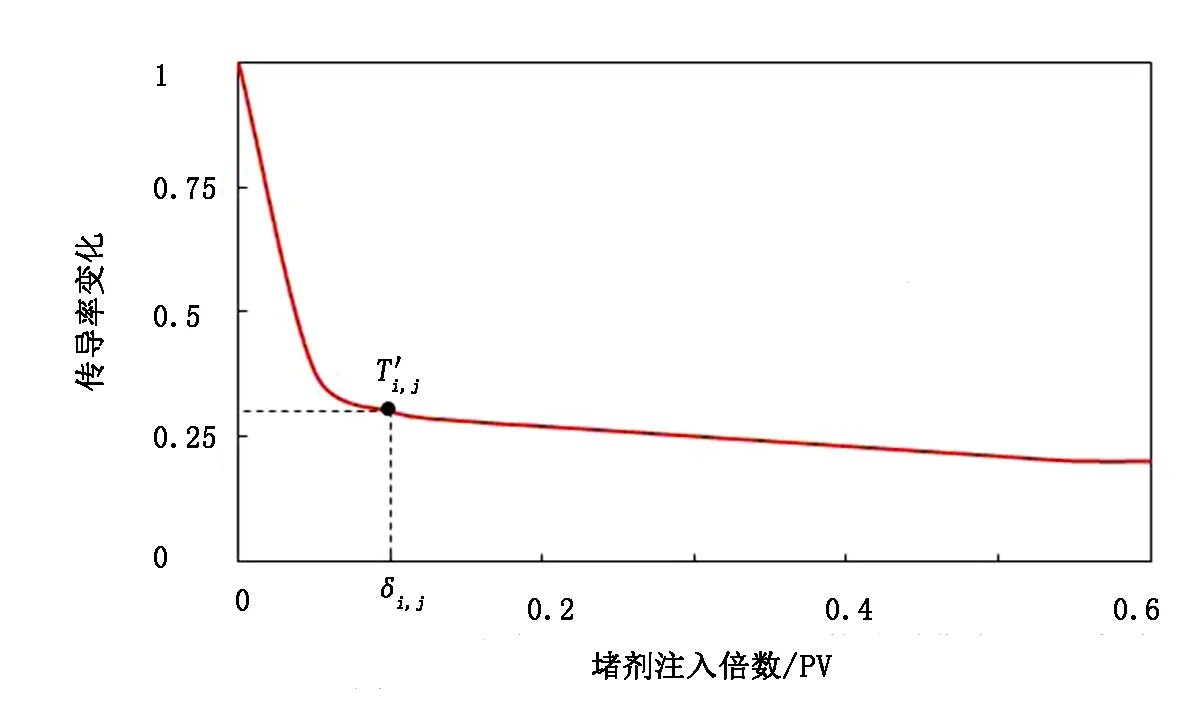
图2 不同堵剂用量与传导率的关系模型Fig.2 The relation model between injection amount of plugging agent and conductivity
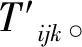
步3 注入堵剂后的动态预测。根据步2修正各连通单元体的传导率,进行物质平衡计算:
(10)
在进行调剖动态预测时,可考虑定流压生产模式,得出调剖后油水井注采量变化:
(11)
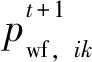
(12)
图3以某调剖井为例说明调剖动态预测过程,Ⅰ1为调剖井(注水井),与4口生产井相连,图3(a)为传导率和连通体积;图3(b)为当前时刻Ⅰ1井的注水劈分系数。设Ⅰ1井注入堵剂量为350m3,则4个连通单元体的堵剂进入量如图3(c)所示。根据图2关系曲线,得到每个连通单元体的渗流能力变化倍数,最终得到的注入堵剂后传导率分别为0.096、0.232、0.472、0.112m3/(MPa·d)(见图3(d))。可以看出,对于传导率较大、窜流严重的连通单元体,其传导率在调剖后的变化值也就越大,从而实现了各连通单元体的均衡调剖。
该方法不需要复杂地质建模过程,克服了传统数值模拟在引入调剖后繁琐的计算流程,在识别油藏高渗通道的基础上,直接沿水窜方向进行调剖模拟,实现了优选调剖井、模拟调剖动态的无缝对接,形成了一套主要利用日常生产数据即可快速进行大规模调剖动态模拟方法,更适于实际工程应用。
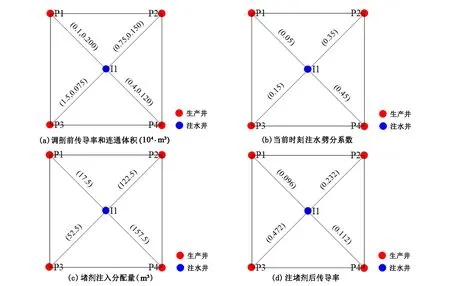
图3 Ⅰ1井调剖动态预测过程示意图 Fig.3 The process of predicting dynamic performancebased on injection profile control
3 实例应用
3.1 非均质概念油藏
利用商业数值模拟软件建立一个二维非均质双层油藏模型,采用五点法井网,共有4口注水井和9口生产井,油藏网格划分为81×81×2,X、Y和Z方向的网格尺寸为15、15和10m。模型真实渗透率场如图4所示,分布有高渗和低渗条带,第1层渗透率级差小,平均渗透率为254mD,第2层渗透率级差大,平均渗透率为450mD,平均孔隙度为0.2,初始含油饱和度为0.8,油藏初始压力为25MPa。以商业数值模拟软件模拟生产1500d的生产指标进行动态拟合优化,其模拟时间需要114.8s,笔者方法仅需0.95s,计算速度提高约120倍。
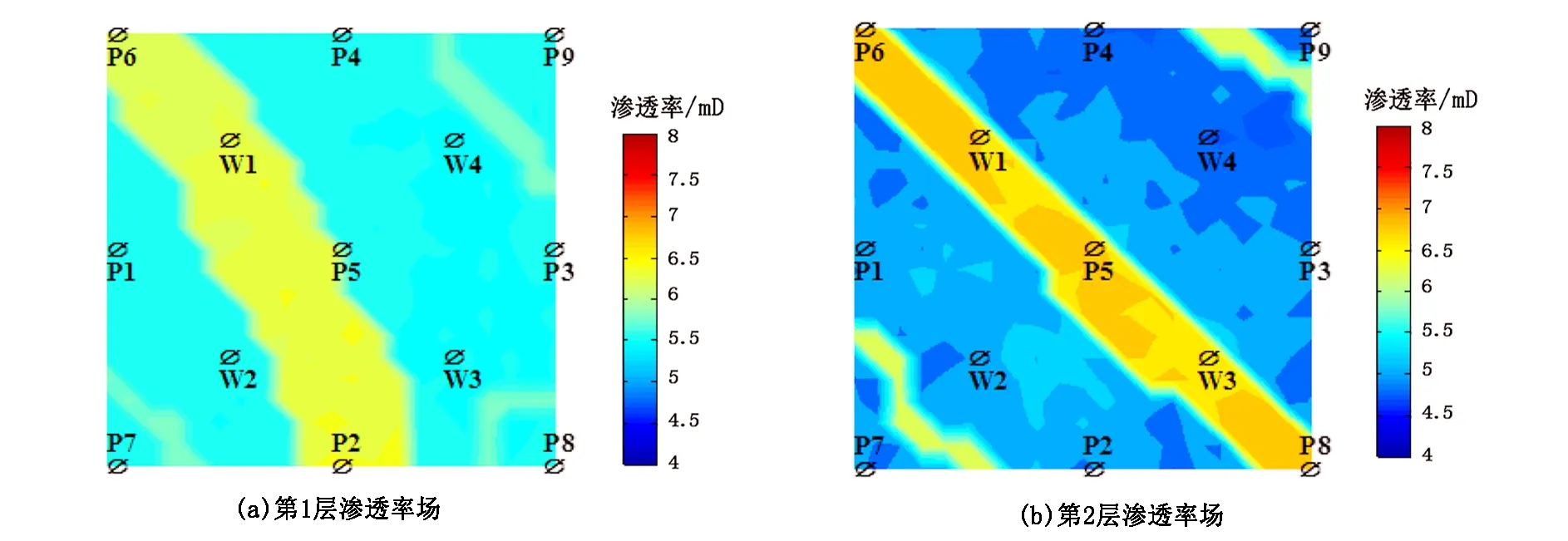
图4 非均质模型真实渗透率场(对数刻度)Fig.4 The true permeability field of heterogeneous model (logarithmic scale)
图5为含水率拟合结果,对比可以看出,笔者方法动态拟合效果较好,图6为注水井注水效率计算结果,图7为数值模拟软件计算流场与笔者方法计算注水劈分系数的对应情况,可以看出,两者对应性较好,验证了笔者方法的准确性,可用于后期调剖动态预测。历史拟合反演后的连通参数如图8(a)、(c)所示,图中数据直观地显示了各连通单元体的传导率,红色线表示优势传导方向,蓝色线传导能力一般,灰色线最差。
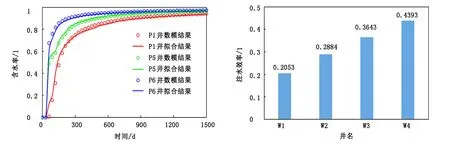
图5 部分生产井含水率拟合结果 图6 各注水井注水效率Fig.5 The comparison of water cut of some Fig.6 The water injection efficiency of each injector producers after history matching
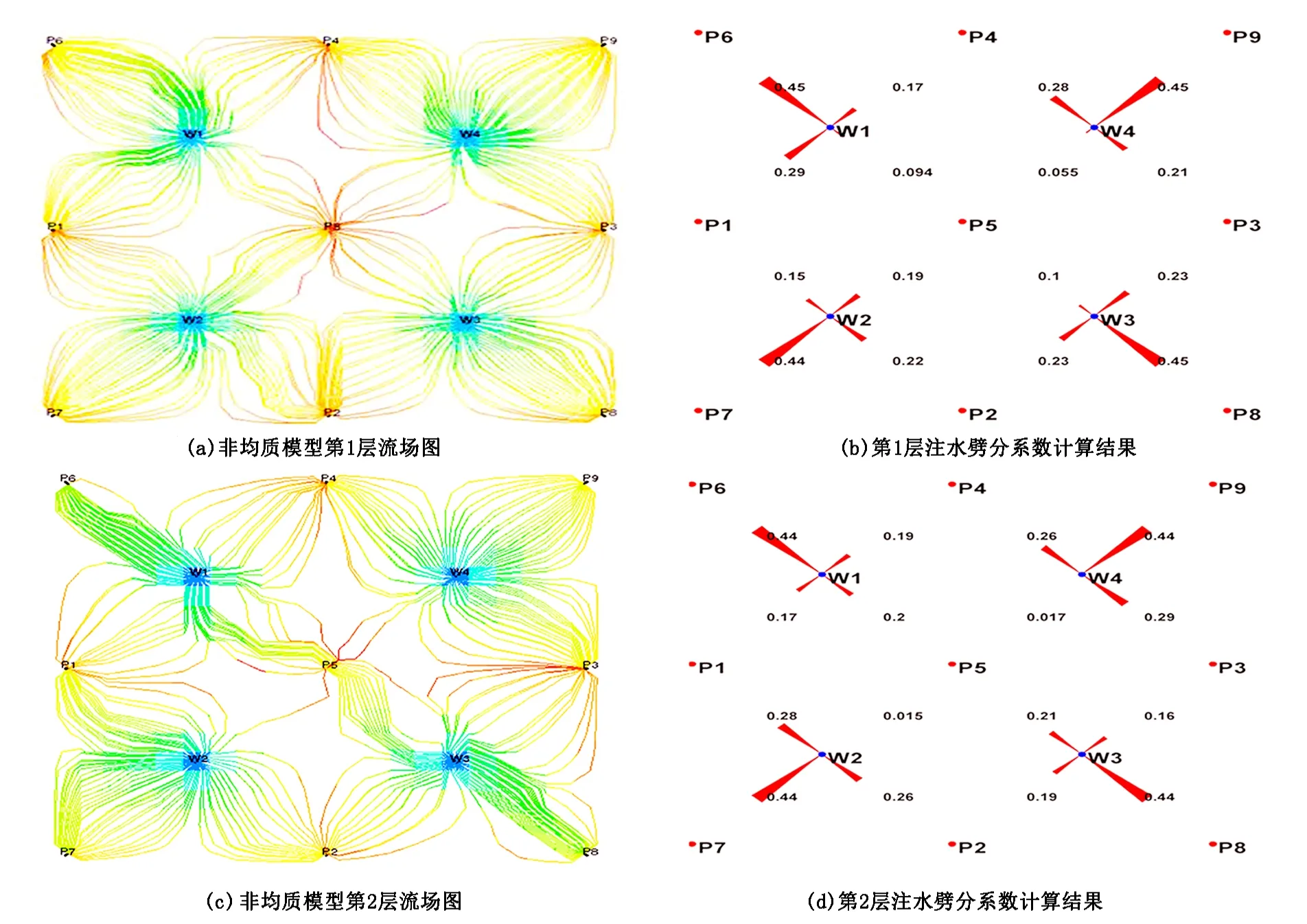
图7 模型流场与笔者方法劈分系数计算结果的对应情况Fig.7 The comparison between the flow field of the model and allocate factors calculated by methods proposed in this paper
由图6可知,注水井中W1的注水效率最低,选择W1井进行调剖预测周边生产井生产动态变化。使用图2的封堵率曲线,图8(b)、(d)为加入堵剂后的传导率场,原先优势传导方向的传导率有一定的下降,反映注入的堵剂优先对优势通道进行了封堵,1500d后开始注入堵剂,预测堵剂注入后300d的动态指标变化,堵剂初始用量为500m3,预测结果如图9所示。

图8 调剖前后传导率变化情况Fig.8 The conductivity performance before and after injection profile control
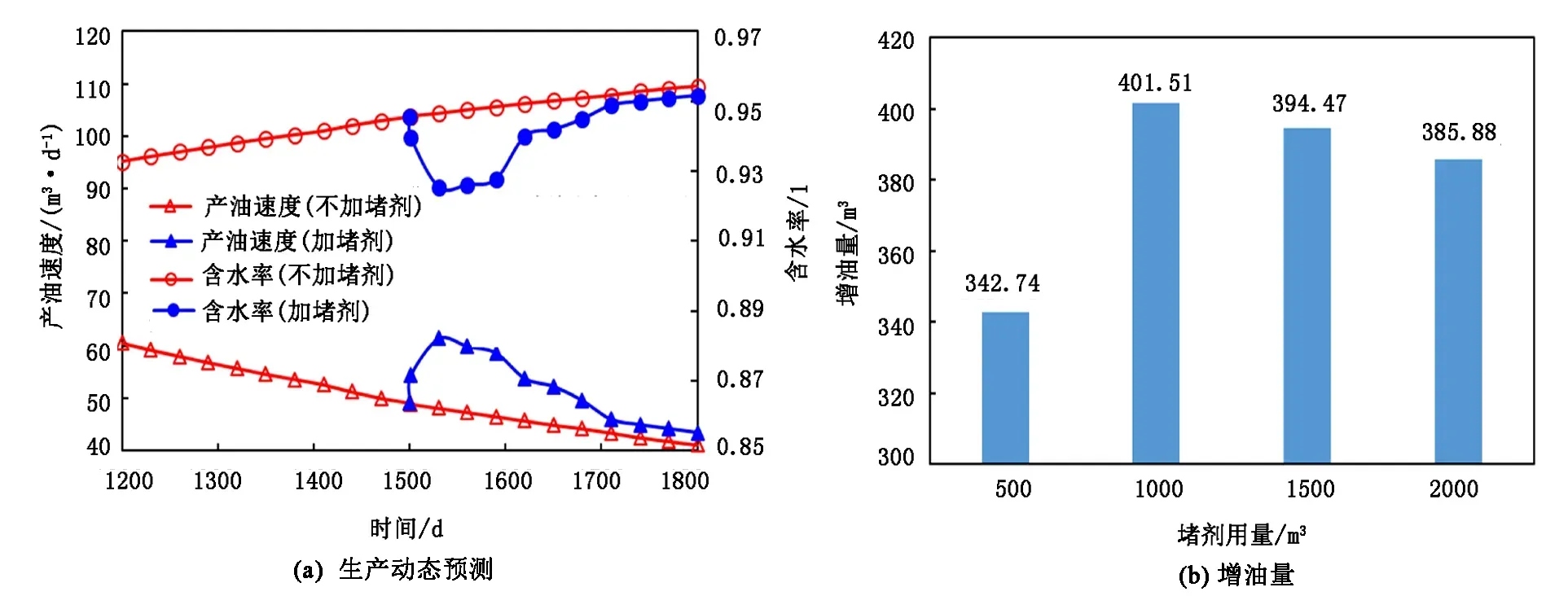
图9 注水井W1调剖后动态预测结果Fig.9 Production forecasts after injection profile control of injector W1
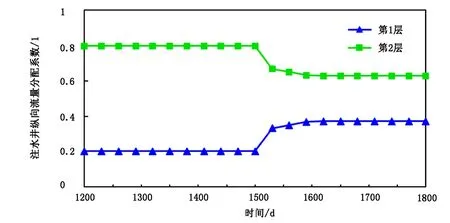
图10 注水井W1流量分配系数曲线Fig.10 The flow distribution coefficient curve of injector W1
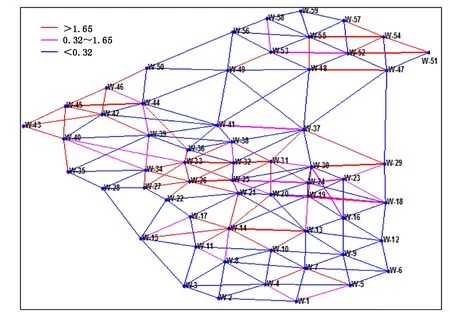
图11 某实际油藏区块主力层井间传导率反演结果Fig.11 The inversion result of interwell conductivity of main layer in a real field
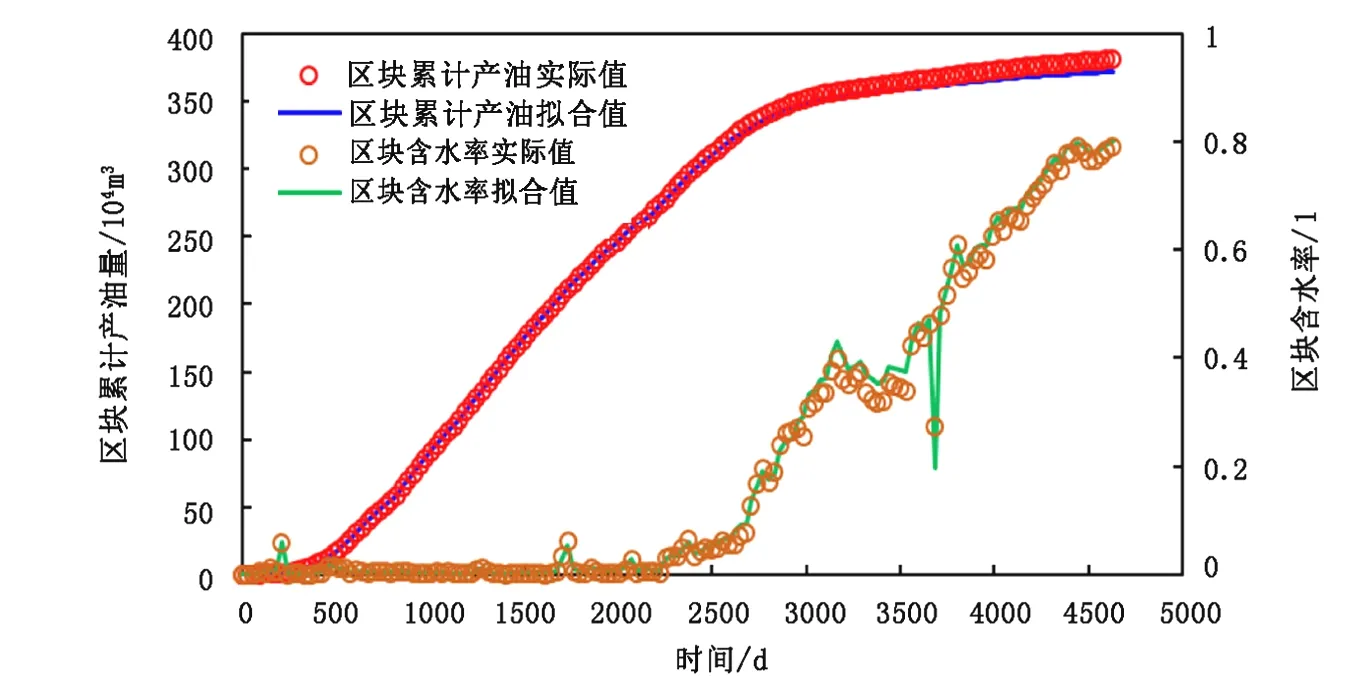
图12 区块生产指标历史拟合结果Fig.12 The history matching result of field quantities
堵剂优先进入传导率大的方向,从图9(a)看出,在注入堵剂约100d内,W1井组含水率下降,产油速度上升,之后含水率缓慢回升,产油速度下降。为确定W1井组最优的堵剂用量,需计算不同堵剂用量的单井增油效果,得出最优值。图9(b)为不同堵剂用量时W1井组增油情况,可以看出,当堵剂用量为1000m3时,单井增油最多,之后随着堵剂用量的增加而增油量下降。此时注水井W1井纵向上的流量分配系数如图10所示,随着堵剂的注入,W1井在纵向上第2层的流量分配系数降低,第1层增高,在纵向改善了驱油效果。
3.2 实际油藏
将笔者提出的调剖动态预测方法应用于某实际油藏区块,该区块于2006年开始生产,有25口生产井和24口注水井,平均渗透率为70mD,平均孔隙度为0.18,油藏初始压力为21MPa。区块主力层井间传导率反演结果如图11所示,图中蓝色线表示传导率小于0.32m3/(d·MPa),粉色线表示传导率在0.32~1.65m3/(d·MPa)之间,红色线表示传导率大于1.65m3/(d·MPa)。区块生产指标拟合结果如图12所示,区块累计产油量和含水率拟合较好。
基于连通性反演结果,优选了5口注水井进行调剖。统计矿场试验和室内试验得到的堵剂对地层渗流能力的影响数据,通过多元回归得到封堵率曲线如图13所示,极限封堵率为75%,使用该封堵曲线。根据正交试验设计计算各调剖井的堵剂用量如图14所示,平均堵剂用量为488m3。在4600d开始注堵剂,预测结果如图15所示,2年内区块产油速度平均提高15m3/d,区块含水率平均降低1.58%。其中,现场对生产井W-38实施了调剖作业,其产油速度的增加量为3.8m3/d,使用笔者方法预测该井产油速度的增加量为3.33m3/d,验证了该方法的有效性。
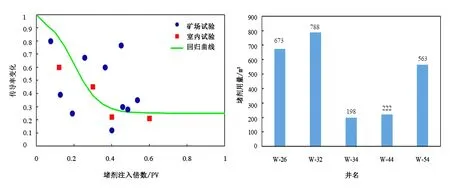
图13 堵剂注入量与渗流能力关系曲线 图14 各调剖井的堵剂用量 Fig.13 The relation curve between injection amount Fig.14 The plugging agent dosage of each well of plugging agent and seepage capacity -controlled by injection profile
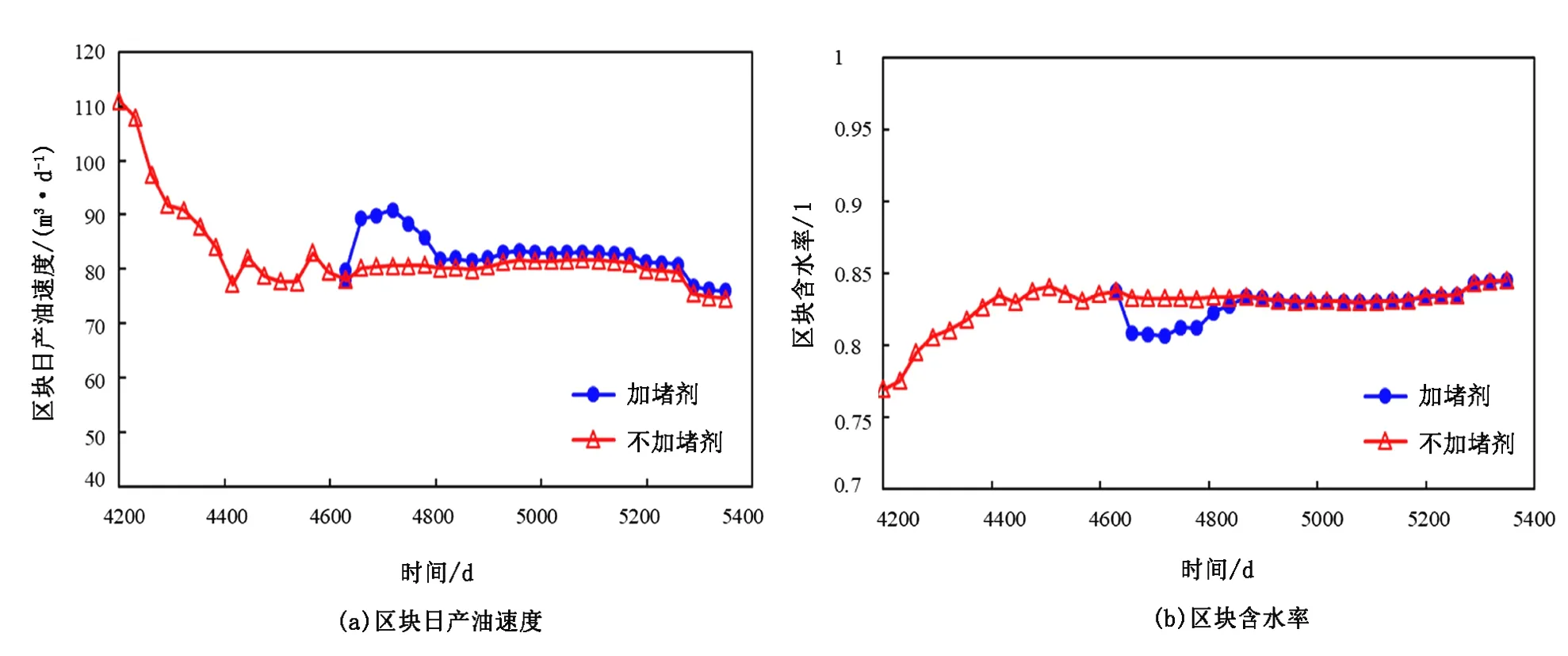
图15 调剖前后区块生产指标预测结果Fig.15 Production forecasts of field quantities before and afterinjection profile control
4 结论
1)考虑多层油藏特点,建立了一种可快速模拟油水动态的多层INSIM模型。在此基础上,考虑调剖堵水作用机理,结合调剖剂室内试验结果,建立了一种油藏调剖动态预测新方法。
2)相比于传统数值模拟方法,建立的数据物理驱动模型只需利用注采数据即可自动建模,无需复杂地质建模过程,模型直接沿着连通方向进行流动处理,不需太过精细的渗流方程,可以和油藏优势流道识别无缝对接。
3)非均质概念算例结果表明,该方法反演得到的连通性结果与数值模拟软件一致,验证了数据物理驱动模型的可靠性;实际算例应用,计算了各调剖井的最优堵剂注入量,模拟预测产油速度和含水率的变化,达到了降水增油效果,预测效果与现场实施效果较为相近,可较好地指导实际现场应用。

