基于离散趋近律与无差拍双闭环结构的单相LCL型PWM整流器控制策略

李景灏 吴爱国

基于离散趋近律与无差拍双闭环结构的单相LCL型PWM整流器控制策略

李景灏 吴爱国

（天津大学电气自动化与信息工程学院 天津 300072）

对于单相LCL型PWM整流器，传统双闭环控制以PI控制为电压外环，电流内环常采用以变换器侧电流为受控量的无差拍控制。该方案存在两个问题：①电压外环的积分器会限制系统动态性能；②无法精确实现网侧单位功率因数。为此，该文提出一种以离散趋近律控制为电压外环、以改进无差拍控制为电流内环的双闭环控制策略。对于电压外环，该文推导网侧半波电流峰值与该半波周期内直流侧电压增量之间的数学关系，在此基础上提出一种离散趋近律控制策略。对于电流内环，提出一种以网侧电流和变换器侧电流的加权和为受控量的改进无差拍算法，并给出实现精确单位功率因数所需的电流参考值。该文还讨论网侧电流欠阻尼振荡引起的电流过冲问题，并提出解决方法。仿真和实验结果表明，所提双闭环控制显著改善了系统动态性能，且实现了精确网侧单位功率因数。

单相PWM整流器 LCL型滤波器 离散趋近律 无差拍控制 欠阻尼振荡

0 引言

与传统的不控整流器和相控整流器相比，PWM整流器具有网侧接近单位功率因数、谐波注入少、可实现能量流动的双向控制等优点，已经广泛应用于不间断电源、铁路功率调节器、光伏发电等领域。在一些应用场合，对PWM整流器的动态性能有较高要求。为此，已有不少文献对PWM整流器的先进控制算法进行了研究，以期在不改变主电路参数设计的情况下实现系统动态性能的改善。

对于单相PWM整流器，通常采用电压、电流双闭环控制。一种思路是令电压外环采用PI控制器产生参考电流幅值，将该值与电网电压锁相信号相乘后得到电流内环的交流参考信号，并采用PR控制器对该交流信号实现无稳态误差跟踪。基于这种思路，文献[1]研究了在离散域中直接进行电流环PR控制器设计的方法。文献[2]基于Lyapunov方法分析了采用PR控制时单相PWM变换器非线性动态过程的稳定性，并提出了控制器参数的整定原则。这种控制思路虽然有效，但难以实现有功、无功功率的解耦控制。另一种思路是采用类似于三相PWM整流器的基于旋转坐标变换的有功、无功功率解耦控制方法。通过引入虚拟正交量，可将单相整流器模型变换为两相正交的交流系统，进而像三相PWM整流器一样实现有功、无功的解耦控制。基于这一思路，文献[3]推导了旋转坐标系下的电流环解耦数学模型，设计了∞控制器，提高了电流环动态性能和系统鲁棒性。文献[4]提出了一种基于二阶数字有限长单位冲激响应（Finite Impulse Response, FIR）陷波器和功率前馈方案的改进控制策略，提高了系统动态性能。考虑到引入虚拟变量的过程会产生1/4电网周期的控制延迟，导致系统稳定性和动态性能的下降。文献[5]利用变换器参数直接构造了虚拟正交量，避免了控制延迟的产生。文献[6]提出了一种任意相位延时算法，理论上可将控制延迟缩短至一个采样周期，但需要考虑抗干扰问题。为了进一步提高系统动态性能，一些文献将无差拍和模型预测控制方法引入到单相PWM整流器控制中。文献[7]提出了一种改进的无差拍电流预测控制方法，避免了控制延时导致的电流畸变。文献[8]提出了一种基于牛顿插值的功率前馈无差拍控制算法，改善了动态响应和电流预测精度。文献[9]提出了一种基于最小电流误差的模型预测电流控制，改善了动态响应并实现了零稳态误差。文献[10]提出了一种包含积分补偿环节的模型预测控制。文献[11]提出了一种基于调制电压矢量优化的定频模型预测电流控制。这些方法不同程度地改善了单相PWM整流器的稳态和动态性能。上述研究都是针对单相L型变换器讨论的。对于单相LCL型变换器，文献[12]利用扩张状态观测器推导了一种仅需检测网侧电流的电流环解耦控制策略。文献[13]研究了仅采用网侧电流反馈实现功率控制与有源阻尼的参数优化方法。文献[14]提出了一种利用网侧电流高频分量反馈实现有源阻尼的方法。文献[15-17]讨论了基于LCL型滤波的三相变流器的电流控制策略，其结果可为单相LCL型整流器的控制提供借鉴。

从现有文献来看，对于单相PWM整流器的控制，多数文献仅停留在对电流环的优化上，电压环仍采用传统的PI控制。实际上，PI控制器中的积分环节正是制约系统动态性能的主要因素，故有必要从电压环着手进行控制系统的优化设计。趋近律方法是一种用于设计滑模控制到达过程的方法。作为滑模控制策略的一部分，趋近律方法已经广泛应用于电力电子领域[18-24]。基于合适的趋近律设计，状态变量能够快速到达滑模面，使系统获得优良的动态性能[25]。为此，本文首先推导了网侧半波电流峰值与该半波周期内直流侧电压增量之间的数学关系，并采用离散趋近律方法设计了电压外环控制器。另一方面，对于单相LCL型整流器，现有的以变换器侧电流为受控量的无差拍控制会导致网侧偏离单位功率因数。为此，本文提出了一种以网侧和变换器侧电流的加权和为受控变量的改进无差拍控制，减小了网侧功率因数偏差，并进一步推导了实现精确网侧单位功率因数所需的电流参考值。通过进一步分析，本文指出了网侧电流欠阻尼振荡可能引起电流过冲的问题，并给出了消除电流过冲的方法。最后，通过仿真和样机实验验证了所提方法在稳态和动态性能方面的优势。

1 单相LCL型PWM整流器数学模型

单相PWM整流器拓扑如图1所示。图1中，交流侧滤波器采用了LCL型滤波器，g、分别为网侧电感和变换器侧电感，g、分别为网侧电感和变换器侧电感寄生电阻，f为交流侧滤波电容，f为无源阻尼电阻，为直流侧支撑电容，为负载电阻，S1～S4为功率开关管。

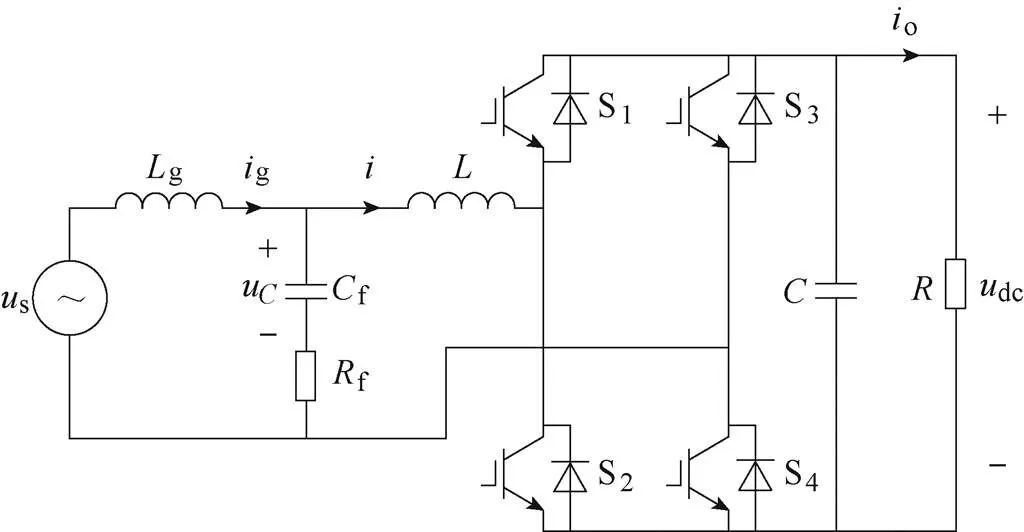
图1 单相PWM整流器拓扑

根据图1所示主电路结构，可以得到LCL型整流器的数学模型为

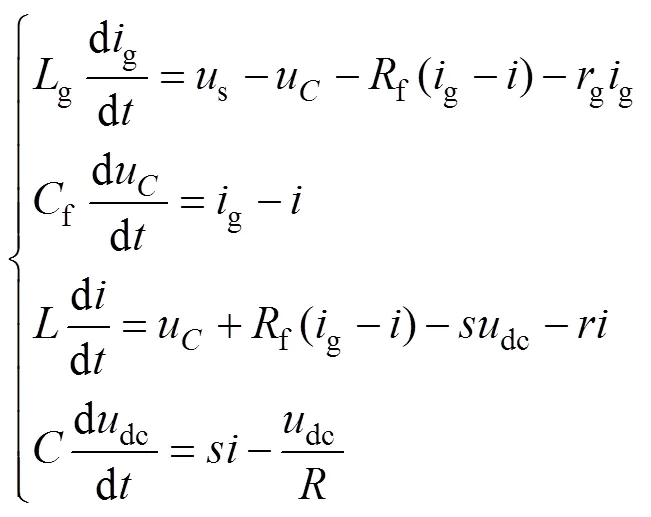
式中，g为网侧电流；为变换器侧电流；u为交流侧滤波电容电压；s为电网电压；dc为直流侧电压；为开关函数，其定义为

经过状态空间平均化处理后，为与电网电压s同频率的交流量。

2 基于离散趋近律的电压外环控制器

本节从电压外环着手，为了优化单相LCL型PWM整流器的控制性能，提出一种基于离散趋近律的电压外环控制算法。与传统的PI控制不同，该算法根据离散趋近律来确定一个半波周期内的参考电流峰值，有利于实现直流侧电压的快速调整。

根据能量守恒定律，在一段时间内由电网发出的能量应等于直流侧电容储能增量、负载消耗能量和寄生电阻损耗、开关管损耗等附加损耗之和。假定网侧电流已被控制为和电网电压同相位，则在一个半波周期内近似的能量平衡关系为

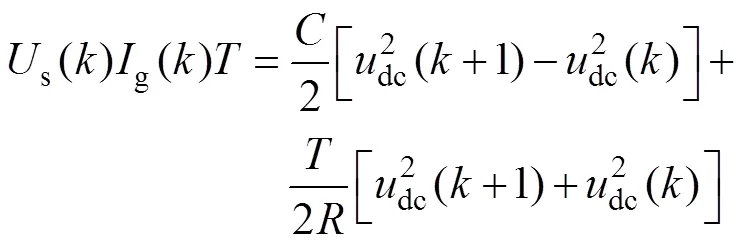
式中，s()、g()分别为第个工频半波周期（0.01s）电网电压和网侧电流有效值；dc()和dc(+1)分别为第个工频半波周期起始时刻和终止时刻直流侧电容电压的瞬时值。考虑到系统工况突变时刻（如负载突变）一般不会恰好落在电网电压过零点处，将定义为：当＞1时，=0.01；当=1时，=0.01-。这里，将突变时刻所在的半波周期定义为“第1个半波周期”，将定义为发生突变时第1个半波周期已经过去的时间。可以看出，从第2个半波周期开始，的取值始终为0.01s。

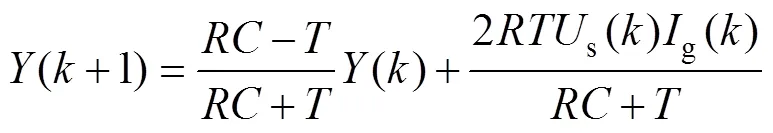
式中，等式右侧第二项与g有关，而g是可控的。因此，可将式（4）看作以g为输入，为输出的离散时间线性系统。由此，得到了反映单相PWM整流器直流侧电压动态过程的离散化数学模型。该模型形式简单，且能很好地反映不同峰值的半波交流电流产生的直流侧电压增量。

定义误差量为

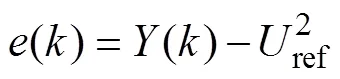
式中，ref为直流侧电压参考值。将式（5）代入式（4），可得

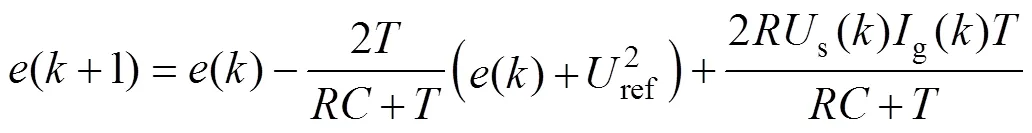
采用如下的离散趋近律，即

式中，0＜＜1。由压缩映射原理可知，当()按照式（7）规律变化时，会逐渐趋近于0。

由式（6）、式（7）可求出实现该趋近律所需的网侧电流有效值，即

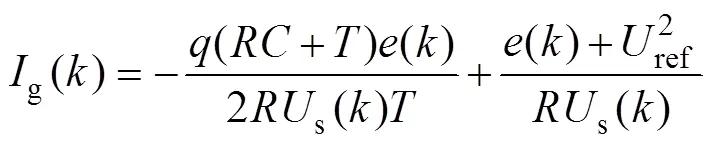
考虑到输出电压偏差较大时（如起动过程），可能出现过高的电流参考值[26]，故实际应用趋近律算法时需对电流有效值进行限制，即取

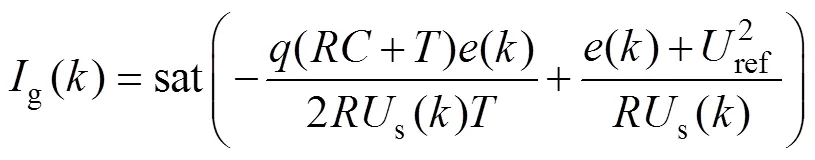
其中

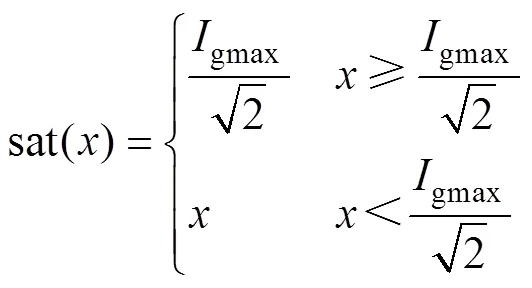
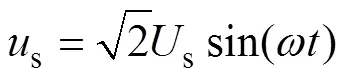
通过合理设计电流内环控制器，即可实现对网侧电流参考值的跟踪控制。第3节将具体阐述电流内环控制策略。

3 改进无差拍控制算法

无差拍控制是一种精确的电流控制算法，具有动态响应快、易于数字实现等优点，常用作单相PWM整流器的电流内环控制算法。该算法的基本思路是根据变换器的数学模型计算被控对象输入端所需控制量。本节首先指出现有的无差拍控制算法存在的不能实现精确单位功率因数的问题，并提出一种改进的无差拍控制算法。

3.1 改进无差拍控制算法的推导

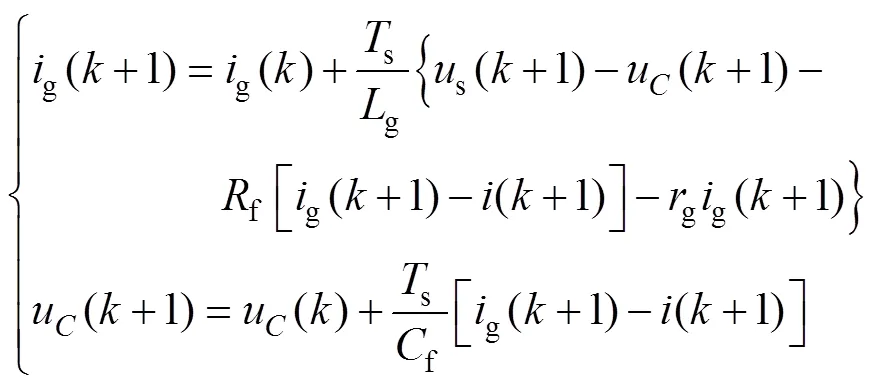
为了实现对网侧电流参考值的精确跟踪，应有g(+1)=()和(+1)=*()。其中，()、*()为时刻的电流参考值。联立式（11）的两式，消去u(+1)，可得

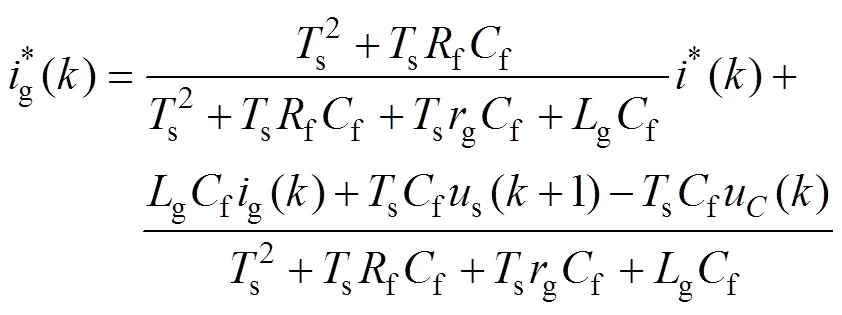
由式（12）可将网侧电流参考值转换为变换器侧电流参考值。采用前向差分法对式（1）的第三式进行离散化处理，可得

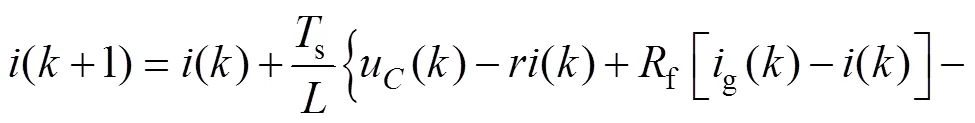
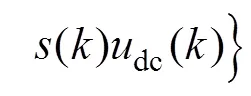
将(+1)=*()代入式（13），可得

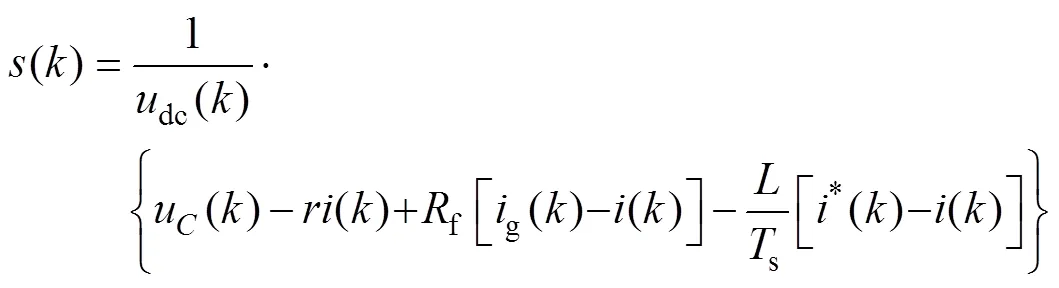
式（12）、式（14）提供了一种精确的单相LCL型整流器网侧电流无差拍控制算法。根据该算法，在第个采样周期[s, (+1)s]的初始时刻获取u()、()、g()、dc()等变量值和电流参考值*()后，即可根据式（12）、式（14）计算得到控制器作用量，使得第+1个采样周期的初始时刻的电流值与给定值相等。容易看出，该算法需要同时对g、、u进行采样，且依赖于所有变换器参数，计算过程比较复杂。

为了避免这种复杂性，考虑到交流侧滤波电容f数值很小，文献[27]采用了一种简化的无差拍算法（下文称为“简化算法”）。该算法忽略了滤波电容电流，即令=*，只使用式（14）作为控制律。与式（12）、式（14）构成的精确算法相比，简化算法不检测网侧电流g，无需参数f，对系统状态和参数的依赖较少，且计算量小，易于实现。然而，简化算法并不能直接控制网侧电流，采用该算法会使得网侧偏离单位功率因数。另外，简化算法检测变量为滤波电容电压u和变换器侧电流，无法直接获得滤波电容电流值。若要在不增加额外电流传感器的情况下实现有源阻尼，只能对电容电压作微分运算，这增加了算法实现的难度。

为了解决上述问题，本文提出一种适用于LCL型整流器的改进无差拍算法。首先，对LCL型整流器的数学模型进行变换，使其在数学模型形式上与L型整流器相似。将式（1）第一式与第三式相加后得

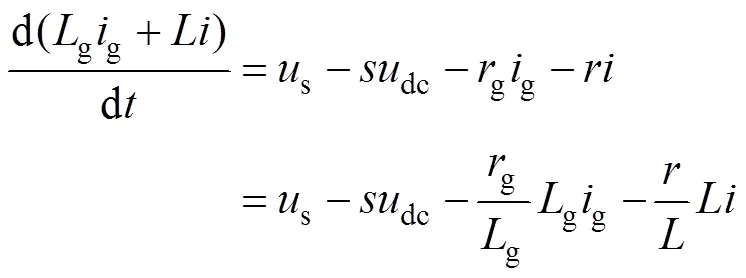
由于电感寄生电阻上的压降很小，为获得形式简单的公式，近似认为

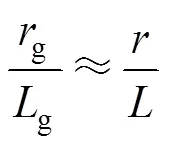
取g=，sum=g+，为网侧电感与变换器侧电感的比例因子。由此，可将式（1）变换为

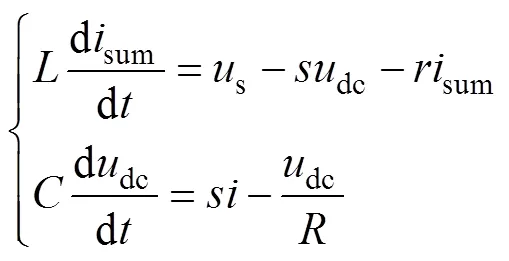
式中，交流侧电容电压作为中间变量被消除。式（17）在形式上与L型整流器的数学模型十分相似。类似于简化算法思路，暂时忽略交流侧滤波电容电流，则稳态时有g≈，即sum≈(1+)g≈(1+)，sum在稳态时近似与g、成正比。因此，对于电流内环，可令

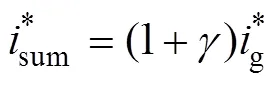
并采用sum作为受控变量来设计控制器。采用前向差分法对式（17）第一式作离散化处理，有

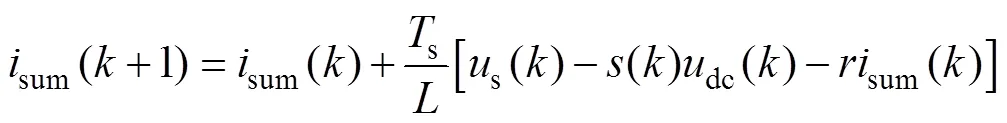
式（18）、式（20）即构成本文提出的改进无差拍控制算法。由于忽略了交流侧电容电流，改进算法会导致网侧偏离单位功率因数，但与文献[27]中的简化算法相比，改进算法引起的功率因数偏差较小。另外，改进算法的检测变量为网侧电流g和变换器侧电流，将二者相减后可直接获得滤波电容电流值，将滤波电容电流值作简单的比例反馈即可实现有源阻尼。可见，与文献[27]中的简化算法相比，改进无差拍算法不仅使系统更接近单位功率因数，且利于实现有源阻尼。

在实际实现过程中，由于DSP运算处理需要时间，由第个周期采样值计算得到的占空比直到第+1个周期才能起作用，存在一拍滞后。为了消除这种延迟的影响，可对各变量加一拍预测，即

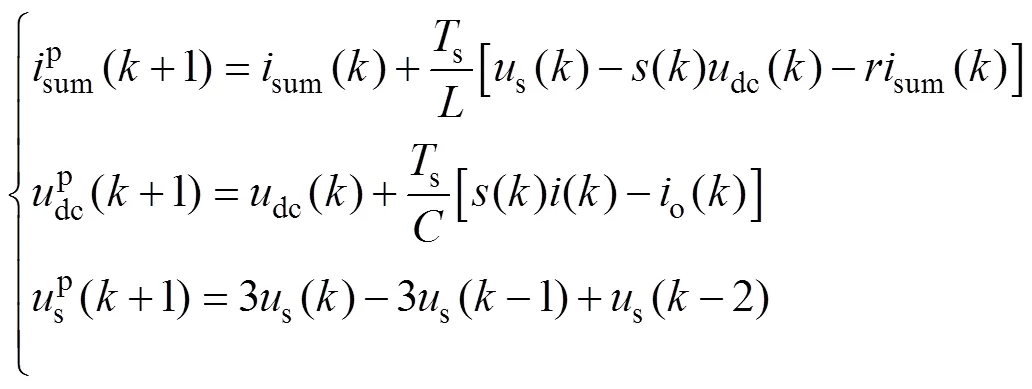
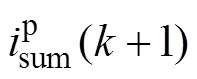
3.2 功率因数误差分析与修正

前文已指出，当采用本文提出的改进算法或文献[27]算法时，由于忽略了交流侧电容电流，稳态时网侧会偏离单位功率因数。本节将对这两种算法造成的功率因数误差进行分析，并针对本文算法提出一种功率因数修正方法。

（1）考虑本文提出的改进无差拍算法。此时sum被控制为与电网电压完全同相。令s=msin(t)，sum=g+=msin(t)，m、m分别为电网电压和sum幅值，m=(1+)，将s、sum代入式(1)第一、第二式，整理后可得

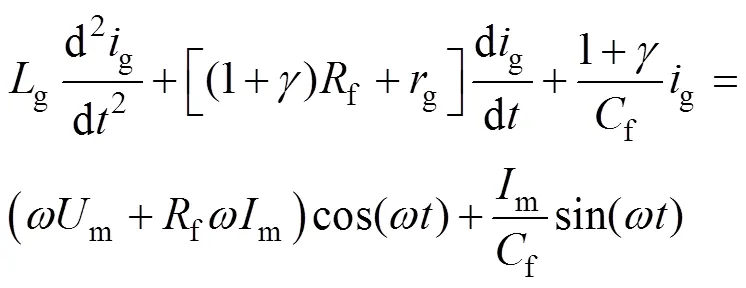
由于f、g数值较小，为了突出重点，忽略其相关项。令g=gmsin(t+g)，gm、g分别为网侧电流和幅值和相位，将g代入式（22）可得

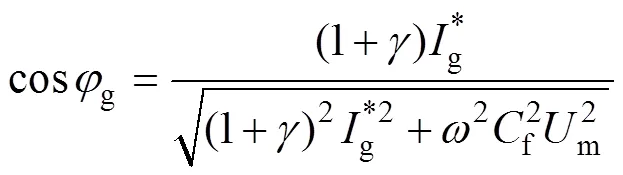
（2）考虑文献[27]中的简化算法。此时变换器侧电流被控制为与电网电压完全同相。令s=msin(t)，=sin(t)，g=gmsin(t+g)，类似地，可求得

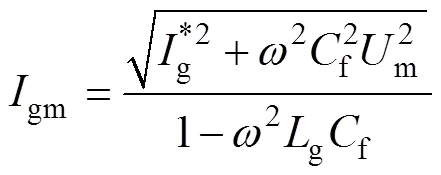
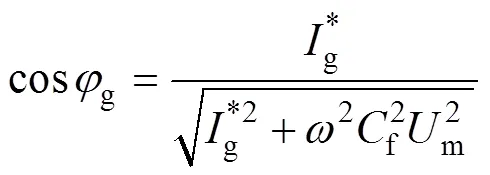
容易看出，当f=0时，对于两种算法均有=gm，cosg=1，这是期望获得的理想情况。由于滤波电容的存在，网侧电流的幅值和相位都偏离了预期，导致电网侧偏离单位功率因数。值得指出的是，比较式（24）和式（26），可以看出

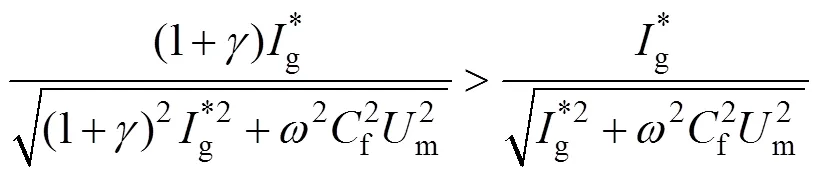
这表明，与简化算法相比，本文提出的改进无差拍算法造成的功率因数偏差较小。

为了进一步减小功率因数偏差，针对改进算法，本节给出一种功率因数修正方法。该方法通过给sum参考值加入一定补偿分量，实现精确的单位功率因数。

假定在补偿分量作用下，网侧电流与电网电压实现了严格同相位，即满足s=msin()，g=sin()。将此两式代入式（1）第一、第二式，整理后可得

令u=cmsin(t+)，cm、分别为交流侧滤波电容电压的幅值和相位，则有

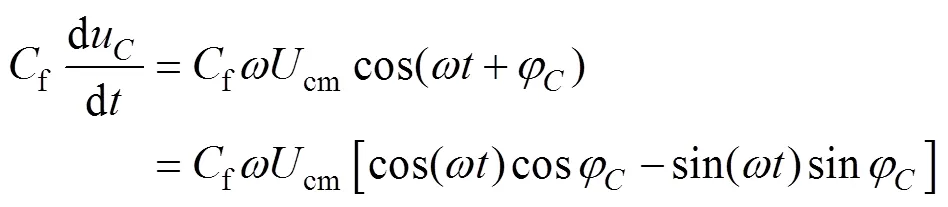
联立式（28）、式（29），可解得

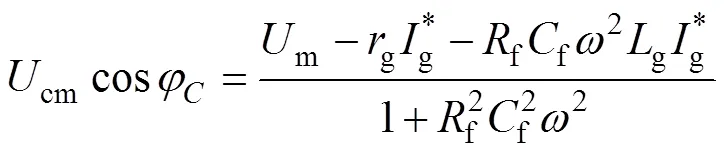
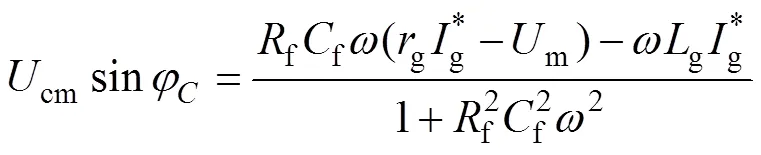
由此，可求解出

1．丹池赤水、石髓金精、山台尽五色金。王罕岭嵊县峧(gǎo)的东南坡山岙，20世纪60至70年代已筑有眠牛湾水库，库水流出的水渠中，目前依然能看到古人所说的丹池赤水这一奇观；在眠牛湾水库坝大面积的护坡块石上，同样可以看到石髓金精、山台尽五色金的壮丽场面。

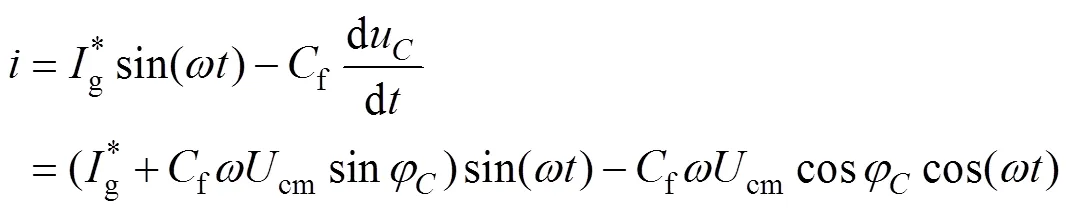
故sum的参考值应取为

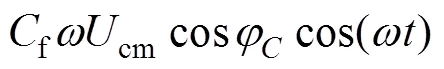
由式（33）可看出，该表达式包括一个与电网电压同相位的分量和一个超前电网电压90°（滞后270°）的分量。若按照式（33）设定sum参考值，则理论上能使g=sin(t)，即电网电压与网侧电流同相位，实现精确的单位功率因数。

将式（10）代入式（18）或式（33）即可形成加权和电流sum参考值。采用无差拍控制算法式（20）对该参考电流进行跟踪，即形成了本文提出的离散趋近律与改进无差拍双闭环控制算法。该算法不仅保留了无差拍控制高动态性能的优点，还进一步优化了电压外环的动态响应速度，有利于系统整体性能的提升。值得注意的是，式（8）给出的参考电流有效值依赖于变换器的模型参数，且该式的推导过程忽略了附加损耗。实际电路中，由于参数失配和附加损耗的影响，若完全依赖式（8）确定参考电流，可能导致直流侧电压存在稳态误差。为此，当直流侧电压接近参考值时，可以加入PI控制器对参考电流进行修正，以消除稳态误差。离散趋近律与无差拍双闭环控制算法框图如图2所示。

4 LCL型整流器系统欠阻尼分析及网侧电流过冲消除方法

由于LCL滤波器是三阶系统，在实际应用中还需考虑可能存在的谐振或欠阻尼振荡问题，保证系统安全可靠运行。本节将结合改进无差拍控制策略对系统阻尼进行分析，指出网侧电流欠阻尼振荡可能导致暂态电流出现过冲，并提出了消除电流过冲的方法。

根据式（17），可得整流器交流侧电压rec(rec=dc)到sum的传递函数为

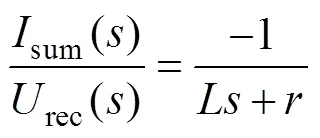
可见，若以sum为受控变量，则系统被控对象为一阶惯性环节。进一步考虑sum与g的关系，将式（1）前两式写成与sum关联的形式，有

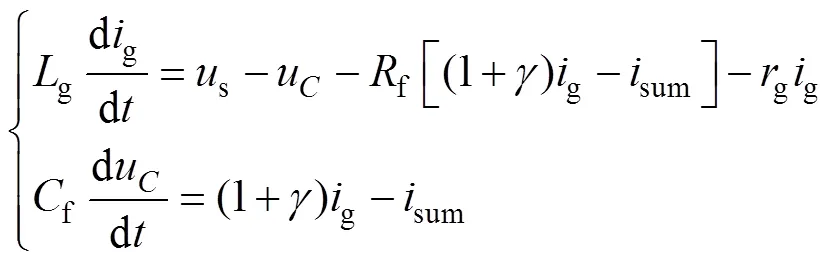
则sum到g的传递函数为

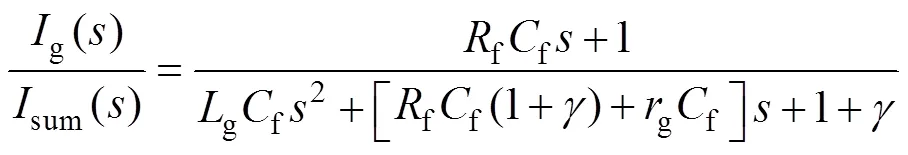
当f、g、均为零时，有

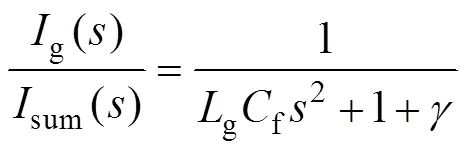
由此可见，虽然从rec到受控变量sum的传递函数没有谐振点，但sum到g的传递函数存在谐振点。这一谐振点与rec到g传递函数的谐振点相同。这表明，LCL型滤波器的固有谐振点并没有因为受控变量的改变而发生变化。进一步可看出，f能为LCL型滤波器提供额外阻尼，有效抑制谐振尖峰，这就是无源阻尼的原理。由文献[28]可知，采用电容电流比例反馈时，也可为系统提供额外阻尼，即有源阻尼方法。当采用本文提出的改进无差拍控制策略时，由于已经检测了网侧电流和变换器侧电流，可将二者作差直接得到电容电流，通过比例反馈方便地实现有源阻尼。

然而，加入无源或有源阻尼后，虽然能避免谐振的发生，但当网侧电流突变时，暂态过程中仍可能出现欠阻尼振荡现象，产生较大的暂态峰值。sum和g仿真结果如图3所示。图3a、图3b分别给出了采用改进无差拍控制策略时加权和电流sum和网侧电流g的仿真结果。单相PWM整流器参数见表1。仿真时采用150V恒压源替代直流侧电容，这样可以单独实施电流闭环控制。图3中，=0.045s时，网侧峰值电流参考值由5A阶跃至10A（对应的sum峰值由6.7A阶跃至13.3A）。由图3a可看出，当参考值突变时，加权和电流迅速跟上，暂态过程没有振荡。这表明采用改进无差拍控制算法可以实现对sum的快速、精确控制。由图3b可看出，网侧电流g为精确的正弦波形，表明改进无差拍算法能实现精确的网侧电流控制。当网侧电流在峰值处由5A阶跃至10A时，暂态过程中出现了欠阻尼振荡现象，g存在较大的过冲。这是因为在设置的仿真参数下由sum到g的传递函数式（36）为欠阻尼系统。

为了避免由欠阻尼振荡引起的暂态电流过冲，可将式（18）或式（33）给出的sum参考值做一阶低通滤波处理，以缓解参考值变化速率，避免出现振荡现象，即令

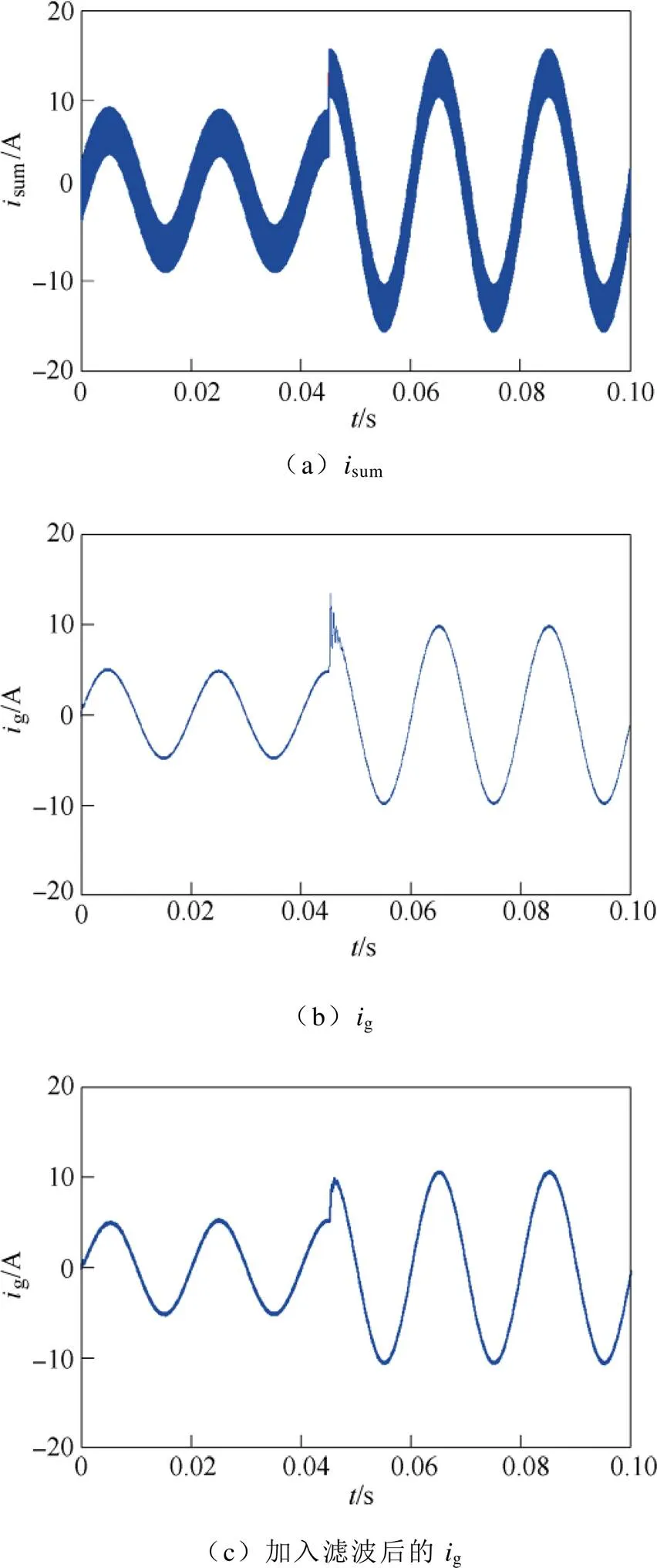
图3 isum和ig的仿真结果

表1 单相PWM整流器参数

Tab.1 Parameters of the single-phase PWM rectifier

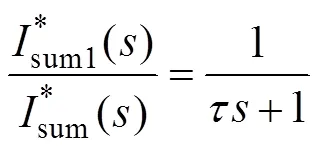
若进一步考虑滤波环节式（38）引入的相位延迟，则实现精确网侧单位功率因数的sum参考值为

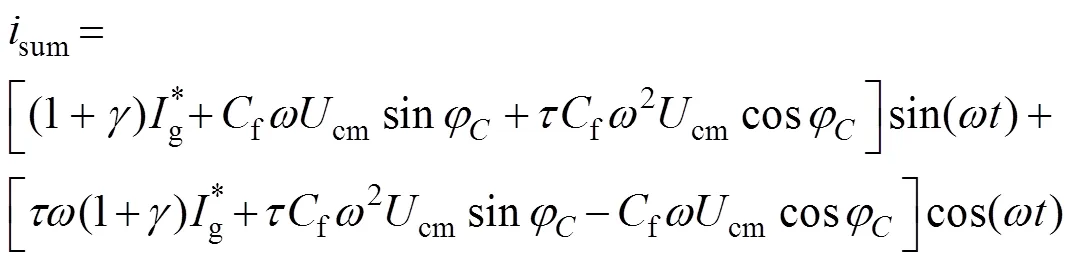
当 =0时，式（39）即为式（33）。

5 仿真分析

本节进一步对离散趋近律与改进无差拍双闭环控制策略进行仿真研究，以验证其稳态和动态性能。仿真时采用式（9）和式（20）作为控制律，采用式（39）作为sum参考值，并采用表1所示参数。

对于稳态性能，从图4～图7的仿真结果来看，无论稳态还是暂态，电网电压始终和网侧电流保持同相位，实现了精确的单位功率因数。图8给出了网侧电流谐波分析结果，可见网侧电流总谐波畸变率（Total Harmonics Distortion, THD）为2.20%，这表明网侧电流具有良好的波形质量。上述结果验证了本文提出的改进无差拍控制算法的稳态性能。

对于动态性能，本文从输出电压在大偏差下的跟随性能和负载突变时的抗扰性能两方面进行验证。相应地，考虑由不控整流突变为受控整流和负载突增两种工况，分别采用PI控制和离散趋近律控制作为电压外环控制律进行仿真（电流内环控制均采用所提出的改进无差拍算法）。

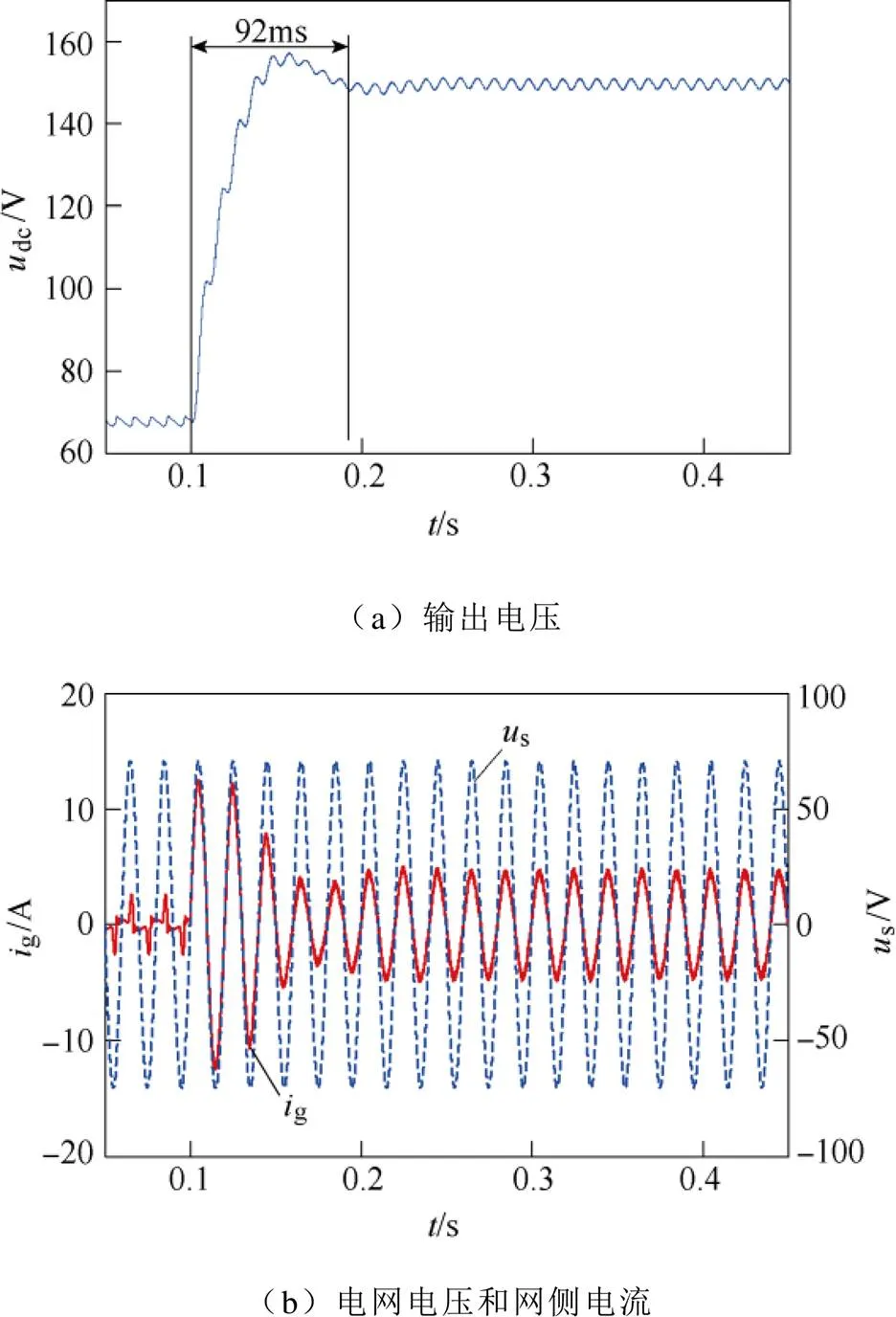
图4 不控整流突变为受控整流仿真结果（PI控制）

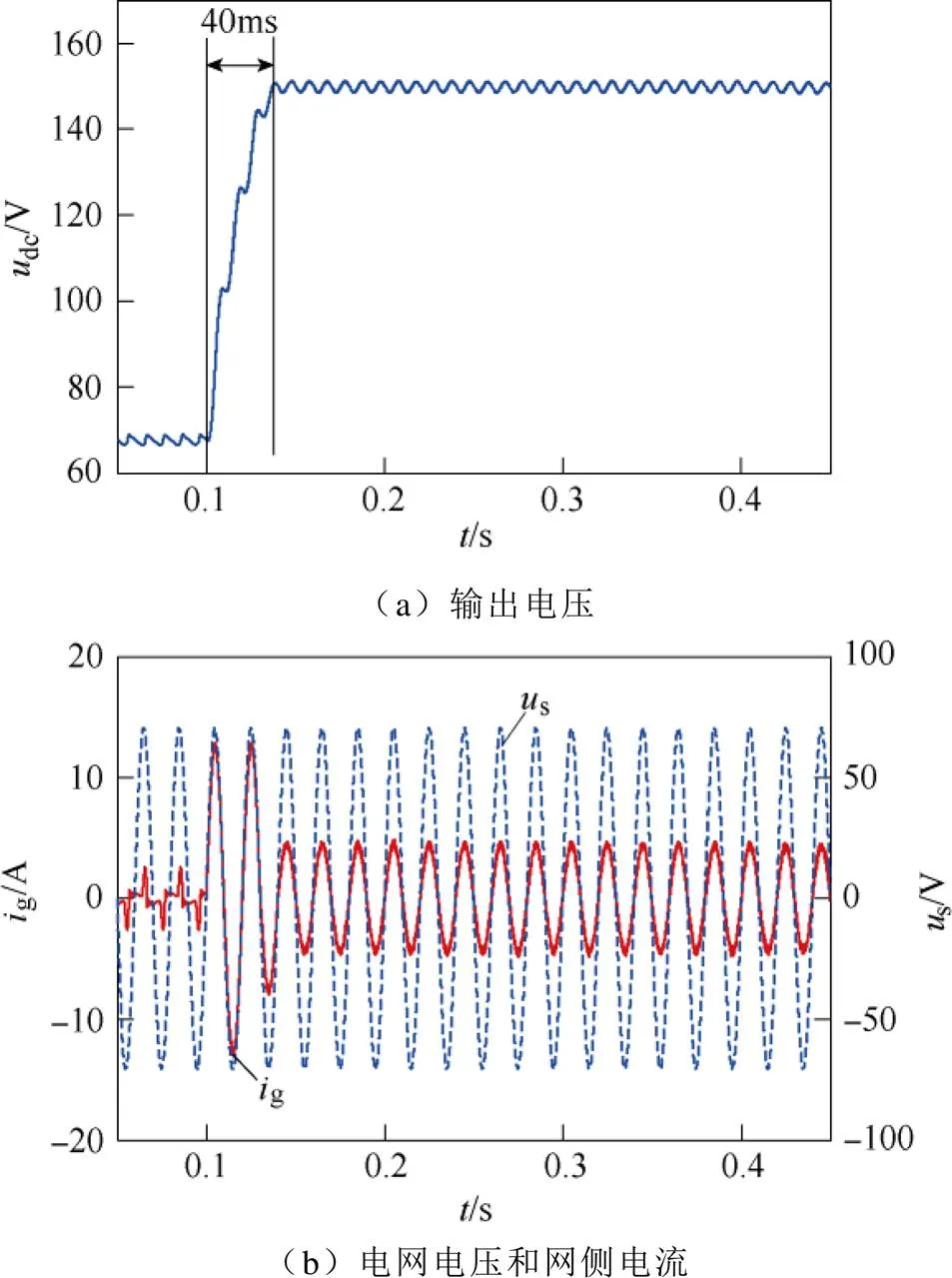
图5 不控整流突变为受控整流仿真结果（离散趋近律控制）

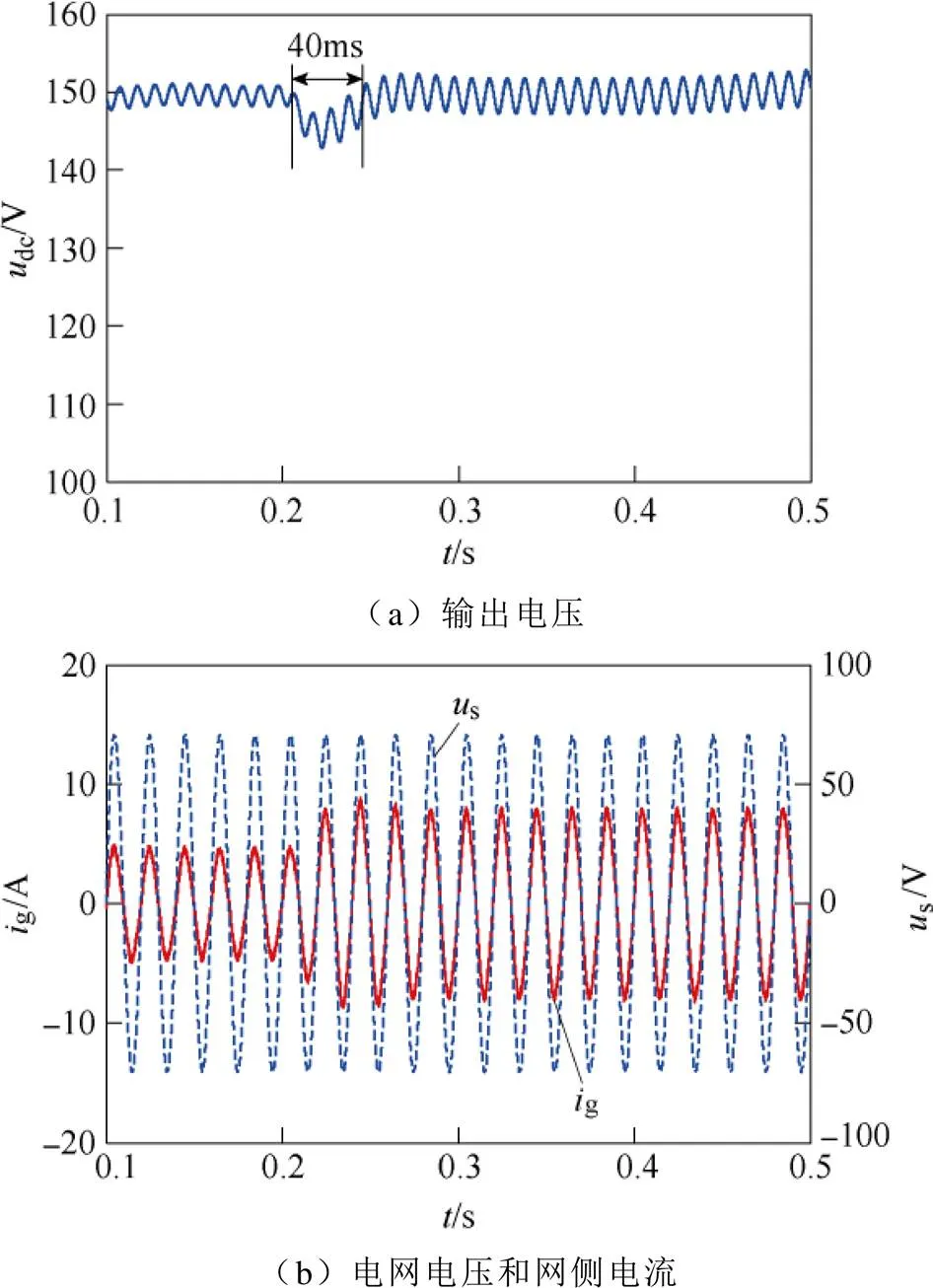
图6 负载突增仿真结果（PI控制）

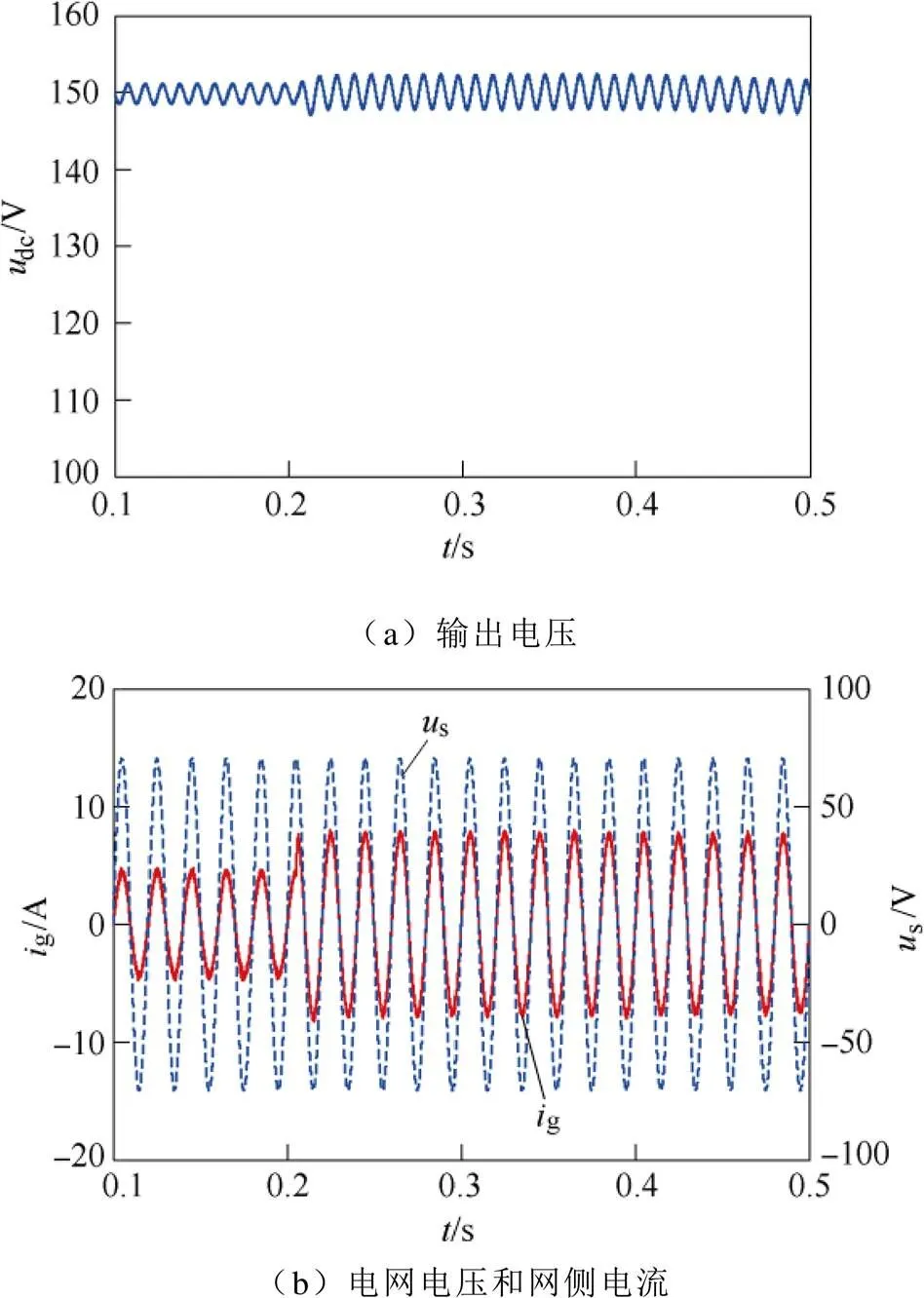
图7 负载突增仿真结果（离散趋近律控制）

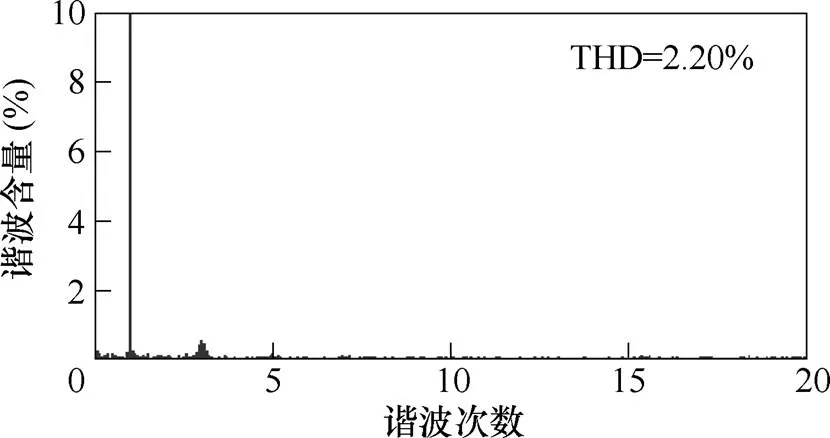
图8 网侧电流仿真数据谐波分析结果（R=86W）

图4、图5给出了两种控制方式下由不控整流突变为受控整流的仿真结果，负载电阻=150W。当=0.1s时，变换器由不控整流突变为受控整流，此时输出电压实际值与参考值之间存在较大偏差。由图4、图5可看出，采用PI控制时，输出电压调节过程大约92ms，存在一定超调；采用离散趋近律控制时，输出电压经过约40ms到达稳态值，调节过程无超调。从网侧电流暂态过程来看，采用离散趋近律控制时，在偏差最大的初始时刻，网侧电流峰值被迅速调节至所允许的最大值，系统以允许的最大功率向直流侧充电，随着输出电压偏差的减小，网侧电流峰值迅速被调节至稳态值。另外，无论电压外环采用哪种控制律，网侧电流g均与电网电压s同相位，实现了精确的单位功率因数。

图6、图7给出了两种控制方式下负载突增工况下的仿真结果。当=0.205s时，负载电阻由150W切换至86W。由图6、图7可看出，采用PI控制时，变换器输出电压出现了约40ms的短时跌落，经调节过程后重新回到稳态值；采用离散趋近律控制时，输出电压几乎没有跌落过程，始终保持为稳态值（只是在负载功率增加后二次纹波幅值增大），而网侧电流峰值则被迅速调节至新的稳态值。

从仿真结果来看，电压外环采用离散趋近律控制时，系统动态性能明显优于采用PI控制时的情况。其原因在于，离散趋近律算法能充分利用所允许的最大网侧电流向直流侧充电，且能迅速调节网侧电流给定值，故输出电压调节速度快；另一方面，离散趋近律算法能保证输出电压误差按趋近律收敛，避免发生电压超调现象，这大大缩短了系统调节时间。对比图4b和图5b可看出，两种控制策略下网侧电流峰值均为12A，意味着二者充电功率峰值相同。这一结果表明，即使在同等的充电功率峰值下，离散趋近律控制能提供的动态性能也明显好于PI控制。这一优势正是得益于离散趋近律控制能保证输出电压无超调。

6 实验结果

为了进一步验证所提算法的实用性，搭建如图9所示的单相PWM整流器实验平台进行了实验验证。控制器采用TI公司的TMS320F28335型DSP，功率器件采用三菱公司的PS21265型IPM。实验系统参数由表1给出，和仿真参数相同。

图9 单相PWM整流器实验平台

6.1 稳态实验

图10给出了采用所提双闭环控制算法时的电网电压、网侧电流稳态波形，负载电阻=86W。图11给出了相应的网侧电流谐波分析结果。由实验结果可看出，电网电压和网侧电流完全同相位，网侧电流THD＜5%，系统具有良好的稳态特性。需要指出的是，实验中测得的网侧电流THD=4.5%，高于仿真中的2.2%。这是因为实验中测得的信号受到了电磁噪声干扰，且实验中使用的网侧电压含有谐波，这些非理想因素使测得的电流波形质量有所下降，但仍满足国标要求。实验结果再次表明，本文提出的改进无差拍控制算法能够实现精确的网侧电流控制和单位功率因数运行。

图10 网侧电流稳态实验波形

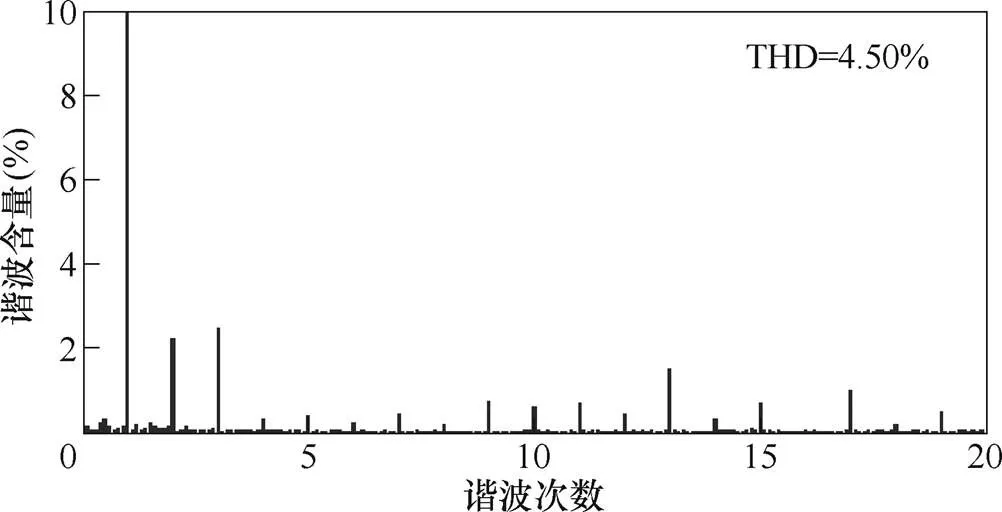
图11 网侧电流实验数据谐波分析结果（R=86W）

6.2 动态实验

为了验证所提出的双闭环算法在动态性能上的优越性，进行了不控整流到受控整流的切换实验和负载突增实验。实验中分别取电压外环控制器为PI控制和离散趋近律控制，电流内环控制器均采用改进的无差拍控制，网侧电流峰值被限制在12A以下。

图12给出了两种电压外环控制器下的不控整流到受控整流切换实验结果。可以看出，当采用PI控制时，输出电压经过约96ms的调节时间进入稳态，且暂态过程存在超调；当采用离散趋近律控制时，输出电压经过约47ms到达稳态值，暂态过程无任何超调现象。这表明，相比于PI控制，离散趋近律控制在输出电压存在大偏差时具有更好的跟随性能。从暂态波形和暂态过程持续时间来看，图12的实验结果与图4、图5给出的仿真结果非常相近。实验结果中，暂态过程持续时间稍长一些，这主要是因为实验电路与仿真模型存在一定误差。

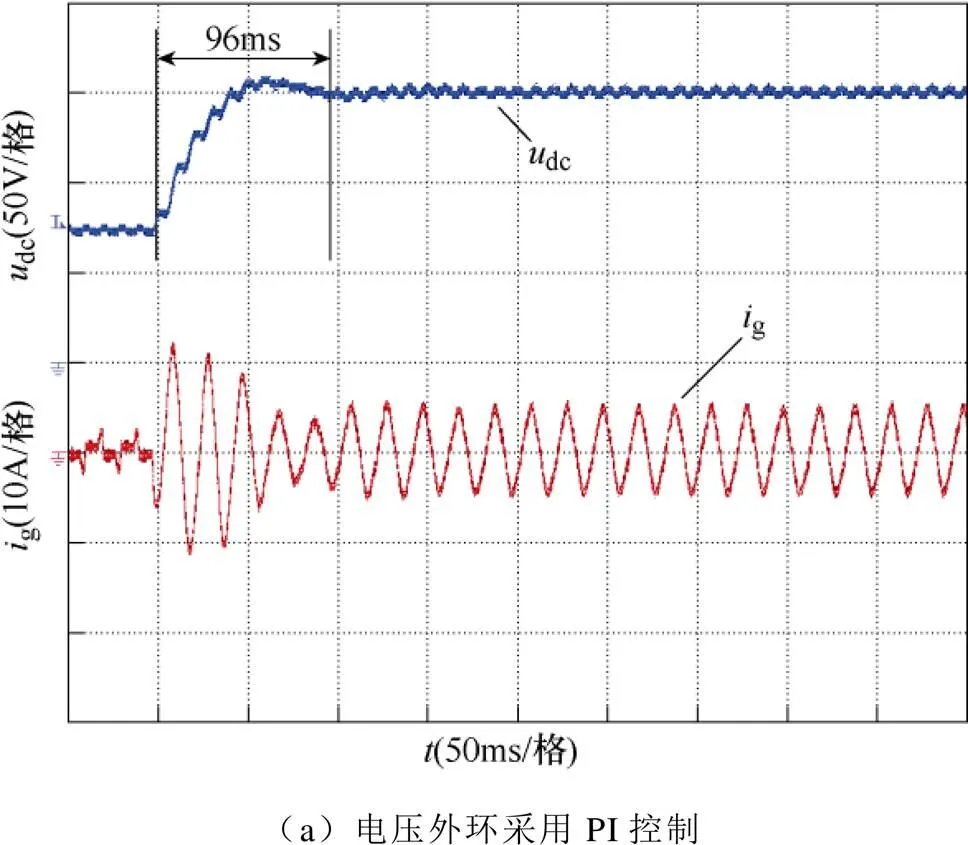
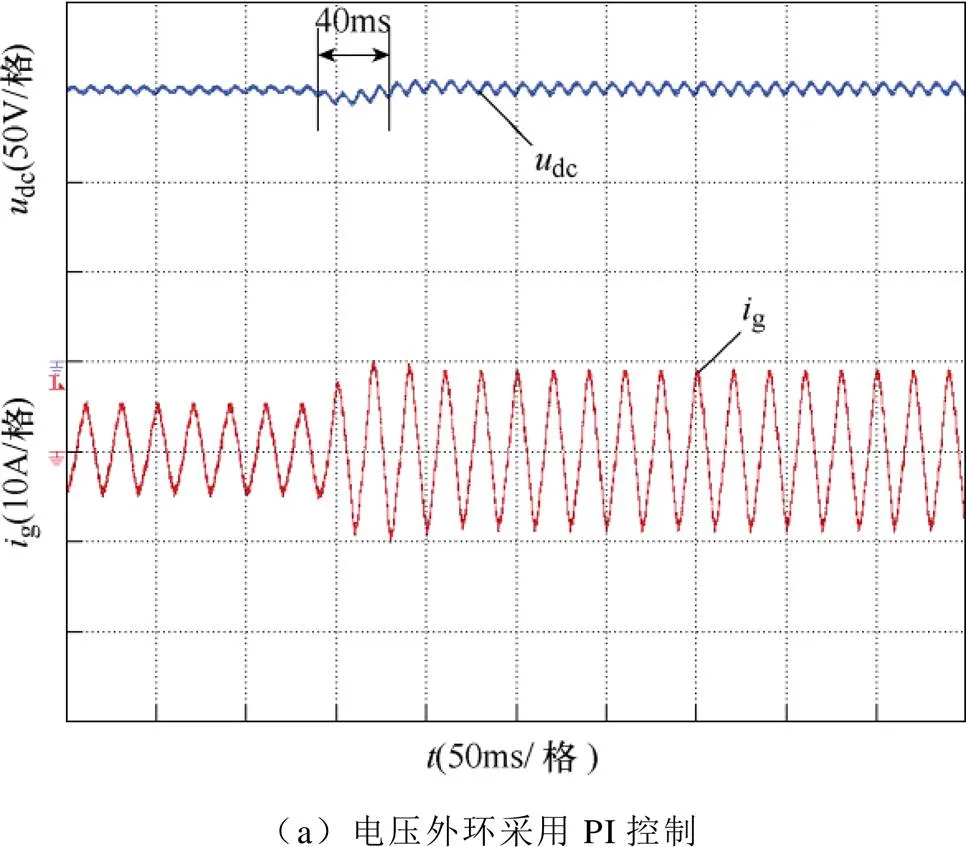
图13给出了两种电压外环控制器下的负载突增实验结果。实验过程中，负载电阻由150W切换至86W，可以看出，当采用PI控制时，输出电压在负载突增时刻出现了大约40ms的短时跌落，网侧电流经过同样的调节时间后进入稳态；当采用离散趋近律控制时，输出电压在负载突增时刻几乎没有跌落，直接进入新的稳态，网侧电流峰值迅速到达新的稳态值，基本没有调节过程。实验结果表明，相比于PI控制，离散趋近律控制具有更好的抗负载扰动能力。图13的实验结果与图6、图7给出的仿真结果非常相近，二者可相互印证。

7 结论

本文对单相LCL型PWM整流器的双闭环控制策略进行了研究。为了优化电压外环动态性能，并解决现有无差拍控制策略存在功率因数偏差的问题，本文提出了一种以离散趋近律控制为电压外环、以改进无差拍控制为电流内环的单相LCL型PWM整流器双闭环控制方法。通过仿真和小功率样机实验对以PI控制为电压外环的双闭环控制策略和所提出的双闭环控制策略进行了对比研究，结果表明，本文提出的双闭环控制策略不仅明显改善了单相LCL型PWM整流器的动态性能，且实现了精确的网侧单位功率因数。

[1] 王剑, 郑琼林, 高吉磊. 基于根轨迹法的单相PWM整流器比例谐振电流调节器设计[J]. 电工技术学报, 2012, 27(9): 251-256.

Wang Jian, Zheng Trllion Q, Gao Jilei. Design of current proportional-resonant regulator for single- phase PWM rectifier based on root-locus method[J]. Transactions of China Electrotechnical Society, 2012, 27(9): 251-256.

[2] Gasca M V, Garcés A, Molinas M. Stability analysis of the proportional-resonant controller in single phase converters[C]//IEEE Workshop on Power Electronics and Power Quality Applications (PEPQA), Manizales, Colombia, 2019: 1-6.

[3] 彭林, 马磊, 刘浩然, 等. 单相PWM整流器H混合灵敏度电流控制[J]. 中国电机工程学报, 2020, 40(14): 4580-4589, 4737.

Peng Lin, Ma Lei, Liu Haoran, et al.Hmixed sensitivity current control for single-phase PWM rectifier[J]. Proceedings of the CSEE, 2020, 40(14): 4580-4589, 4737.

[4] Li Bingzhang, Huang Shenghua, Chen Xi. Perfor- mance improvement for two-stage single-phase grid- connected converters using a fast DC bus control scheme and a novel synchronous frame current controller[J]. Energies, 2017, 10(3): 389-418.

[5] 刘秉, 宋文胜. 基于虚拟信号反馈算法的单相PWM整流器DQ电流解耦控制[J]. 中国电机工程学报, 2018, 38(15): 4504-4513, 4651.

Liu Bing, Song Wensheng. DQ current decoupling control of single-phase PWM rectifiers based on virtual signal feedback algorithm[J]. Proceedings of the CSEE, 2018, 38(15): 4504-4513, 4651.

[6] 张呈象, 葛兴来, 马俊鹏, 等. 基于任意相位延时的单相整流器dq轴电流快速计算方法[J]. 中国电机工程学报, 2017, 37(21): 6400-6409.

Zhang Chengxiang, Ge Xinglai, Ma Junpeng, et al. A fast dq axis current calculation algorithm for single- phase rectifiers based on any phase-delay method[J]. Proceedings of the CSEE, 2017, 37(21): 6400-6409.

[7] 杨立永, 杨烁, 张卫平, 等. 单相PWM整流器改进无差拍电流预测控制方法[J]. 中国电机工程学报, 2015, 35(22): 5842-5850.

Yang Liyong, Yang Shuo, Zhang Weiping, et al. The improved deadbeat predictive current control method for single-phase PWM rectifiers[J]. Proceedings of the CSEE, 2015, 35(22): 5842-5850.

[8] 宋智威, 熊成林, 黄路, 等. 基于牛顿插值的单相整流器功率前馈无差拍控制[J]. 电网技术, 2018, 42(11): 3623-3629.

Song Zhiwei, Xiong Chenglin, Huang Lu, et al. Power feedback-forward and deadbeat control of single- phase rectifier based on Newton interpolation[J]. Power System Technology, 2018, 42(11): 3623- 3629.

[9] 邓知先, 宋文胜, 曹梦华. 单相PWM整流器模型预测电流控制算法[J]. 中国电机工程学报, 2016, 36(11): 2996-3004.

Deng Zhixian, Song Wensheng, Cao Menghua. A model predictive current control scheme for single- phase PWM rectifiers[J]. Proceedings of the CSEE, 2016, 36(11): 2996-3004.

[10] 宋智威, 黄路, 熊成林, 等. 改进的单相脉冲整流器模型预测电流控制策略[J]. 电网技术, 2020, 44(5): 1845-1851.

Song Zhiwei, Huang Lu, Xiong Chenglin, et al. Improved model predictive current control strategy for single-phase pulse rectifier[J]. Power System Technology, 2020, 44(5): 1845-1851.

[11] 刘碧, 宋文胜, 孙可心, 等. 基于调制电压椭圆轨迹优化的单相脉冲整流器模型预测电流控制[J]. 中国电机工程学报, 2018, 38(17): 5177-5188, 5315.

Liu Bi, Song Wensheng, Sun Kexin, et al. Model predictive current control of single-phase PWM rectifiers with elliptic trajectory optimization of the modulated voltage vector[J]. Proceedings of the CSEE, 2018, 38(17): 5177-5188, 5315.

[12] Tang Xiongmin, Chen Weizheng, Zhang Miao. A current decoupling control scheme for LCL-type single-phase grid-connected converter[J]. IEEE Access, 2020, 8: 37756-37765.

[13] 周乐明, 罗安, 陈燕东, 等. 单相LCL型并网逆变器功率控制及有源阻尼优化方法[J]. 电工技术学报, 2016, 31(6): 144-154.

Zhou Leming, Luo An, Chen Yandong, et al. A single-phase grid-connected power control and active damping optimization strategy with LCL filter[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 144-154.

[14] 万晓凤, 聂晓艺, 廖志鹏, 等. 基于误差信号反馈的单相LCL型逆变器谐振抑制方法[J]. 电机与控制学报, 2018, 22(5): 102-109.

Wan Xiaofeng, Nie Xiaoyi, Liao Zhipeng, et al. Resonance damping method of single-phase inverter with LCL-filter based on error signal feedback[J]. Electric Machines and Control, 2018, 22(5): 102- 109.

[15] 张晓, 谭力, 鲜嘉恒, 等. LCL并网逆变器预测电流控制算法[J]. 电工技术学报, 2019, 34(增刊1): 189- 201.

Zhang Xiao, Tan Li, Xian Jiaheng, et al. Predictive current control algorithm for grid-connected inverter with LCL filter[J]. Transactions of China Electro- technical Society, 2019, 34(S1): 189-201.

[16] 程国栋, 吴玮, 夏晶晶, 等. 三相LCL并网逆变器改进模型预测控制策略[J]. 电力电子技术, 2019, 53(7): 14-17.

Cheng Guodong, Wu Wei, Xia Jingjing, et al. Improved model predictive control strategy based on three-phase LCL grid-connected inverter[J]. Power Electronics, 2019, 53(7): 14-17.

[17] 张琦, 李锐, 张永平, 等. 具有主动阻尼特征的LCL并网逆变器状态反馈控制方法[J]. 电工技术学报, 2019, 34(8): 1698-1707.

Zhang Qi, Li Rui, Zhang Yongping, et al. Active damping method based on state-feedback for grid- connected inverter with LCL filter[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1698- 1707.

[18] Rajanna G S, Nagaraj H N. Comparison between sigmoid variable reaching law and exponential reaching law for sliding mode controlled DC-DC Buck converter[C]//International Conference on Power, Energy and Control (ICPEC), Sri Rangalatchum Dindigul, 2013: 316-319.

[19] 刘斌, 粟梅, 贺建军, 等. 混合动力汽车DC/DC辅助电源轨迹规划及双积分滑模控制[J]. 电网技术, 2014, 38(4): 918-924.

Liu Bin, Su Mei, He Jianjun, et al. Trajectory planning and dual-integral sliding-mode control strategy of DC/DC auxiliary power supply for hybrid electric vehicles[J]. Power System Technology, 2014, 38(4): 918-924.

[20] 刘彦呈, 古龙瑞, 张勤进. DC-DC变换器新型趋近律滑模控制[J]. 电力系统及其自动化学报, 2018, 30(1): 64-68.

Liu Yancheng, Gu Longrui, Zhang Qinjin. Sliding mode control of DC-DC converter based on novel reaching law[J]. Proceedings of the CSU-EPSA, 2018, 30(1): 64-68.

[21] Meng Zhiqiang, Shao Wu, Tang Jie, et al. Sliding- mode control based on index control law for MPPT in photovoltaic systems[J]. CES Transactions on Elec- trical Machines and Systems, 2018, 2(3): 303-311.

[22] 李鹏瀚, 王杰, 吴飞. 双馈风电机组次同步控制相互作用的反馈线性化滑模变结构抑制[J]. 电工技术学报, 2019, 34(17): 3661-3671.

Li Penghan, Wang Jie, Wu Fei. Sub-synchronous control interaction mitigation for DFIGs by sliding mode control strategy based on feedback linea- rization[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3661-3671.

[23] 郑长明, 张加胜, 许睿, 等. Buck变换器的鲁棒离散积分滑模控制[J].电工技术学报, 2019, 34(20): 4306-4313.

Zheng Changming, Zhang Jiasheng, Xu Rui, et al. Robust discrete integral sliding mode control for Buck converters[J]. Transactions of China Electro- technical Society, 2019, 34(20): 4306-4313.

[24] 李辉, 周鑫, 陈智勇, 等. 基于重构积分滑模变结构的虚拟无穷大电容器控制策略[J]. 中国电机工程学报, 2020, 40(13): 4340-4348.

Li Hui, Zhou Xin, Chen Zhiyong, et al. The virtual infinite capacitor control strategy based on recon- structed integral sliding mode variable structure[J]. Proceedings of the CSEE, 2020, 40(13): 4340-4348.

[25] Veselic B, Perunicic-Drazenovic B, Milosavljevic Č. Improved discrete-time sliding-mode position control using Euler velocity estimation[J]. IEEE Transactions Industrial Electronics, 2010, 57(11): 3840-3847.

[26] 刘博, 贲洪奇, 白银龙. 一种抑制PWM整流器起动冲击电流的缓给定方法[J]. 电工技术学报, 2018, 33(12): 2758-2766.

Liu Bo, Ben Hongqi, Bai Yinlong. A slow given method to suppress the start-up inrush current of PWM rectifier[J]. Transactions of China Electro- technical Society, 2018, 33(12): 2758-2766.

[27] He Jinwei, Li Yunwei, Bosnjak D, et al. Investigation and active damping of multiple resonances in a parallel-inverter-based microgrid[J]. IEEE Transa- ctions on Power Electronics, 2013, 28(1): 234-246.

[28] 阮新波, 王学华, 潘冬华, 等. LCL型并网逆变器的控制技术[M]. 北京: 科学出版社, 2015.

A Double Closed-Loop Control Method for Single-Phase PWM Rectifiers with LCL Filter Based on Discrete Reaching Law and Deadbeat Algorithm

（School of Electrical and Information Engineering Tianjin University Tianjin 300072 China）

For the single-phase PWM rectifier with LCL filter, the traditional double closed-loop control method usually uses PI compensator as the voltage outer loop controller, and deadbeat control, with the converter side current as the controlled variable, as the current inner loop controller. There are two problems in this scheme: one is that the integrator in the voltage outer loop will limit the dynamic performance of the system; the other is that the unit power factor on the grid side cannot be realized accurately. Thus, this paper presents a double closed-loop control method for the single-phase PWM rectifier, which takes the discrete reaching law control as the voltage outer loop controller and the improved deadbeat control as the current inner loop controller. For the voltage outer loop, the mathematical relationship between the peak value of half wave current on the grid side and the voltage increment on the DC side is derived, and a control strategy based on discrete reaching law is proposed. For the current inner loop, this paper presents an improved deadbeat algorithm with the weighted sum of the grid side current and converter side current as the controlled variable, and derives the current reference for achieving the accurate unit power factor. This paper also discusses the current overshoot caused by the under-damped oscillation, and puts forward the solution. Simulation and experimental results show that the proposed control strategy improves the dynamic performance of the system and achieves accurate unit power factor on the grid side.

Single-phase PWM rectifier, LCL filter, discrete reaching law, deadbeat control, under-damped oscillation

TM46

10.19595/j.cnki.1000-6753.tces.200100

2020-02-04

2020-05-25

李景灏 男，1990年生，博士研究生，研究方向为电力电子与电力传动。E-mail: lijinghao@tju.edu.cn（通信作者）

吴爱国 男，1954年生，教授，博士生导师，研究方向为电力电子变换器与非线性控制技术。E-mail: agwu@tju.edu.cn

（编辑 陈 诚）