鬼成像原理与进展研究

赵生妹，赵 亮，郭 辉，王 乐，郑宝玉

(1.南京邮电大学信号处理与传输研究院，江苏 南京 210003)2.南京邮电大学宽带无线通信与传感网技术教育部重点实验室，江苏 南京 210003

鬼成像（Ghost Imaging，GI）又被称为关联成像（Correlated Imaging），是量子光学领域的前沿和热点之一[1-5]。与传统成像不同，该成像系统包括两支光路，其中一支光路经过待测物体，由桶探测器收集信息（称为信号支路），另一支光路由具有空间分辨率的点探测器收集信息（称为参考支路），通过两支光路的复合测量，能够在没有物体的参考支路中获得物体清晰的像，因而被称为“鬼”成像。由于鬼成像本身的非定域特性，使得它能够解决一些常规成像不易解决的问题，成为分布式图像处理、分布式感知及通信方案等最有力的候选。

鬼成像的思想起源于自发参量下转换（Spontaneous Parametric Down Conversion，SPDC）光子对的纠缠行为[6]。1995 年， Pittman 等[7]首次根据Klyshko的理论完成了在不包含物体的光路上获得待测物体像的实验，证实了量子鬼成像的非定域性，此时鬼成像技术被认为是一种量子关联特性。然而，Bennink等[8]于2002年成功地完成了基于经典光源随机散斑光场的鬼成像实验，该实验说明了鬼成像的实现过程并不一定需要纠缠光源，即经典光场的随机涨落同样也可以实现鬼成像。于是，鬼成像的机理和实现方案引起了人们极大的兴趣[9-17]。特别是Shapiro[18]提出了计算鬼成像理论（Computational Ghost Imaging，CGI），参考支路的光场可通过计算方式，而不是实验探测获取，极大简化了鬼成像实现方案配置。于是，Bromberg等[19]给出了基于单探测器的鬼成像实验方案。作者用一个受电脑控制的空间光调制器（Spatial Light Modulator，SLM）代替旋转的毛玻璃以产生随机散斑光场，利用桶探测器的测量、计算得到待测物体上的散斑值间的关联性，恢复出待测物体的像，因而也称为计算鬼成像。至此，鬼成像实验实现的要求被极大地降低，相关的应用也得到进一步拓展[20]。同时，为提升鬼成像质量和减少鬼成像时间，差分鬼成像[21]、归一鬼成像[22]、正（负）鬼成像[23]和对应鬼成像[24]等方案被提出。此外，信号处理中的压缩感知（Compressed Sensing，CS）技术[25]也被应用于鬼成像，出现了成像质量高、采样时间短的压缩鬼成像[26-28]。不久，计算鬼成像被认识到与单像素成像理论相一致[29]，又出现了多种基于正交变换（如傅里叶变换、正弦变换、哈达码变换等）的高质量单像素成像方法[30-32]。

与此同时，国内研究人员为鬼成像的理论、技术及实用化进程作出了巨大贡献。例如，中国科学院上海光机所韩申生研究小组[33-35]实现了三维关联雷达成像、X射线鬼成像等，极大地拓展了鬼成像研究范畴和应用领域。北京师范大学汪凯戈研究小组对热光一阶干涉和成像进行了系统研究[36]，提出了多波长复用鬼成像等多种方案[37]，拓展了对热光相干性的认识。中国科学院物理所吴令安研究小组首次利用太阳光的二阶相干性提出了日光鬼成像方案[38]，揭示了鬼成像技术从实验室走向实用化的可行性，同时提出了对应鬼成像方案[39]。上海交通大学曾贵华研究小组[40]提出了偏振鬼成像和极限环境下的鬼成像方法。国防科技大学陈平形研究小组[41]提出了基于非负指数散斑调制的快速鬼成像方法。西安交通大学李福利研究小组[42]利用压缩热光实现鬼成像，有效地提高了成像对比度。南京理工大学陈钱研究小组[43]给出了基于计算鬼成像的边缘检测方法等。

鬼成像具有广阔的应用前景和实际应用价值。相对于量子纠缠光源，经典热光源（包括赝热光源或热光源）更容易获取，具有巨大应用前景。因此，本文将以经典赝热光源为例，阐述鬼成像的基本原理，分析影响鬼成像成像质量的基本因素，简述鬼成像技术的最新进展。

1 鬼成像基本原理

图1是鬼成像系统原理示意图。激光器所发出的光经光源调制器后获得可用于鬼成像的散斑光场（常称为赝热光源），其中，散斑记作Ri（x，y），i＝ 1，2，…，N，光源调制器可以是旋转的毛玻璃，也可以是SLM、数字微镜设备（Digital Micro-mirror Device，DMD）或投影仪等，经过分束器分成A和B两支路，A支路（信号支路）在距光源z1处有一待测物体，其投射率函数为T（x，y）（也可以是反射型待测物体），光束透过待测物体（或从物体上反射）后被桶探测器接收，记为探测值Bi，i＝ 1，2，…，N。 B 支路（参考支路）在距离光源z2＝z1处有一个电荷藕合器件（Charge Coupled Device，CCD）采集光场信号，记作Ii（x，y），i＝1，2，…，N。 一方面，信号支路包含待测物体信息，但是由于不对信号支路作任何具有空间分辨的测量，因而不能获取物体的像。另一方面，参考支路的CCD可进行具有空间分辨的测量，但由于参考支路中没有待测物体，因而也不能获取待测物体的像（信息）。但是，通过信号支路和参考支路的关联测量，可以在参考支路上得到待测物体的像，因此，该技术被称为“鬼”成像。

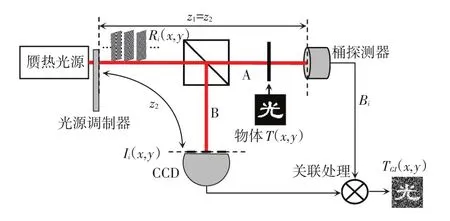
图1 鬼成像系统原理示意图

通过N个不同散斑对待测物体的一系列照射得到对应桶探测值Bi，i＝1，2，…，N，可以表示为

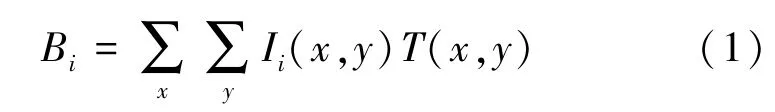
其中，Ii（x，y）可通过 CCD 测量得到，或者通过对Ri（x，y）解光场衍射方程计算获得，Ii（x，y） ＝｜Ri（x，y）*hz（x，y） ｜2，其中，*表示卷积，hz（x，y）表示距离为z处的菲涅尔衍射冲击响应。

假设散斑大小为p×q像素，则N次散斑光场可以改写成矩阵形式，即

其中，每行为一散斑光场，大小为p×q。若同时将待测物体透射系数T（x，y）也写成矩阵形式，且假设待测物体大小也为p×q，即

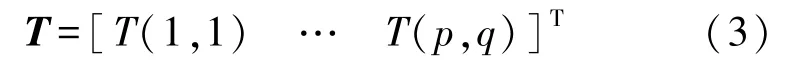
则N次散斑照射获得桶探测器值可表示为

其中，B＝[B1…BN]T为N次桶探测器值。利用两支路光场间关联，通过重构方法，在参考支路可以获得待测物体清楚的像。

2 影响鬼成像质量的关键因素

分析影响鬼成像质量的因素，可以归纳为散斑结构与产生、重构方法和系统优化等几个方面。下面，将分别从这几个方面综述鬼成像技术在相关领域的研究进展。

2．1 散斑结构与产生

鬼成像系统实现中，需要通过一系列散斑对待测物体进行一定次数的照射，从而获得对应桶探测器值。因此，散斑结构和散斑的产生影响着鬼成像系统实现和鬼成像质量。

（1）散斑结构

从目前已提出的鬼成像方案看，其散斑结构基本上可以归纳为两大类，即随机散斑和结构化散斑。

随机散斑是指散斑光场的空间强度分布服从高斯分布或者伯努利分布，其中伯努利分布是二值的随机分布。基于热光光源的鬼成像是利用随机散斑的涨落实现的。但是由于实际中热光光源相关时间很短，普通的光电探测器的响应不够快，不能测出热光瞬时强度的变化；同时普通的热光源强度很低，其光场强度的涨落就很容易被光子的散粒噪声所掩盖。因此，实际上常使用赝热光源替代热光光源进行鬼成像。赝热光源是由一束激光（相干光）被一块旋转的毛玻璃散射而获得[8-9]。毛玻璃的旋转保证了散射光场在时间和空间上都发生涨落，并且其涨落服从高斯分布，很好地模拟出热光光场的统计性质，其中光场的相干面积取决于照射在毛玻璃上光斑的大小，光场的相干时间则由毛玻璃的转速决定。此外，也可在计算鬼成像中，考虑使用SLM等设备产生涨落关系预知的随机散斑。这时，由于光场的分布关系已知，因而不再需要使用CCD探测光场强度的分布情况，而是依据已设计的散斑结构产生不同特性的随机散斑光场，如空间强度分布服从指数分布、瑞利分布、Beta分布、对数正态分布和泊松分布等随机散斑光场[4]。但是，由于 SLM和DMD等设备无法承受大功率的光强，远距离鬼成像场景还是需要通过旋转的毛玻璃实现。

结构化散斑是指散斑的空间强度分布满足特定的结构，常见的如傅里叶散斑和哈达玛散斑。2015年，钟金钢研究小组[30]通过正弦结构的傅里叶散斑照射待测物体，从而直接获得待测物体的傅里叶频谱，再应用傅里叶逆变换便可获得待测物体的图像的单像素成像。该方法的特点在于利用鬼成像建立起待测物体的空域和傅里叶频域的关系，其中，傅里叶散斑的形式可设计为

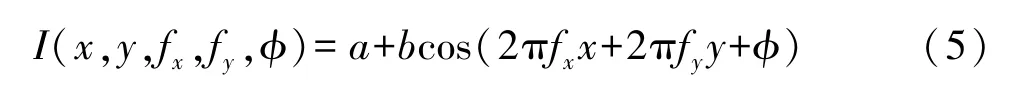
其中，a为直流偏置量，代表散斑的平均能量；b为常数，反映了散斑的能量方差；（x，y）和（fx，fy）分别表示空间坐标和空间频率坐标；φ为初始相位。此时，桶探测器测量结果应与初始相位有关，表示为

另外，笔者研究小组[32]于2016年提出基于快速沃尔什-哈达玛（Walsh-Hadamard）变换的鬼成像方案，使用哈达玛散斑照射待测物体，直接获得物体的沃尔什-哈达玛变换频谱，建立起基于鬼成像的物体空域和沃尔什-哈达玛变换频域间的关系。利用快速沃尔什-哈达玛变换的蝶形递归结构，仅需要Nlog2N次加法运算即可获得成像，极大地减少了重构所需时间。此外，由于哈达玛散斑具有二值特性，因此更易于DMD设备的实现。

通常构造哈达玛散斑的方法是先构造沃尔什-哈达玛矩阵Hk，然后将矩阵的每一个行向量重排得到哈达玛散斑。维数为2的沃尔什-哈达玛矩阵H1为

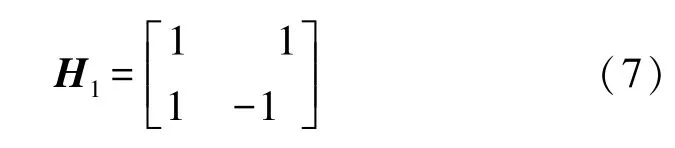
维数为2k的自然顺序的沃尔什-哈达玛矩阵Hk为

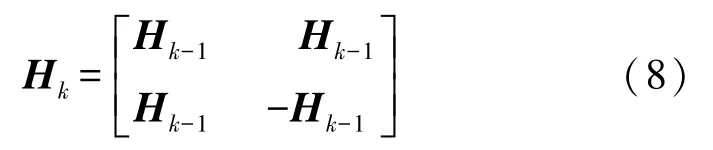
通过式（8）可以预先构造出沃尔什-哈达玛矩阵Hk。但是这种方法需要消耗较大的内存，且需要等待整个沃尔什-哈达玛矩阵构造完成后生成散斑。为此，笔者研究小组[32]给出了一种基于迭代构造哈达玛散斑的方法，以避免消耗过大的内存。其思路是将每个哈达玛散斑都拉伸为一个行向量，则第i个哈达玛散斑的第j个元素h（i，j）可以由迭代公式计算得到，表示如下

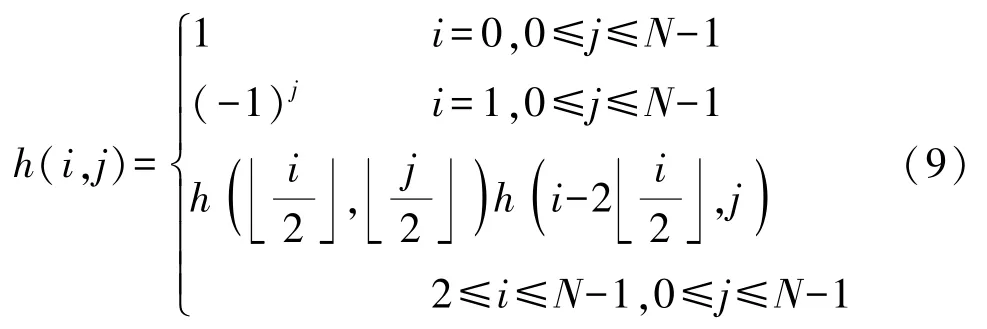
图2 不同散斑下鬼成像结构对比[32]

在此基础上，学者们提出了大量基于Hadamard散斑的构造方法。2017年，孙鸣捷研究小组[44]提出了一种基于“俄罗斯套娃”的Hadamard散光斑构造方法。2019年，李明飞等[45]给出了Hadamard矩阵的优化排序方法。

（2）散斑产生

当完成散斑结构设计后，下一步工作是如何获取这样的散斑，即散斑的产生问题。在早期鬼成像系统中，特别是赝热光源鬼成像实验中，可通过在赝热光源前放置一旋转的毛玻璃获取高斯分布的随机散斑[8]；后来，随着计算鬼成像方案的提出，出现了利用DMD、SLM及投影仪等设备获得随机或结构化散斑的方法[19]。为了进一步提升散斑制备速度，Song等[46]于 2016年设计了利用液晶显示屏（Liquid Crystal Display，LCD）产生结构化散斑的方法。随后，孙鸣捷研究小组[47]于2018年利用FPGA（Field Programmable Gate Array）控制LED阵列实现了1 000帧／s速率的散斑，进一步加快了鬼成像的成像速度。同年，Liu等[48]提出了一种基于光纤相控阵（OFPA）的方案，通过高速电光调制器，调制OFPA实现更快的产生散斑方法。与此同时，徐卓研究小组[49]于2019年利用红绿蓝三彩色 LED阵列实现了100 MHz低光照下的三彩色散斑。

2．2 重构方法

在鬼成像系统中获得桶探测器值及照射待测物体的光场散斑后，后期任务就是在参考支路上重构待测物体。根据不同的散斑，重构方法可以归纳为基于二阶关联的重构、基于压缩感知算法的重构、基于傅里叶逆变换的重构、基于矩阵运算的重构和基于机器学习的重构等几种，现分别描述如下。

2.2.1 基于二阶关联的重构方法

2.2.2 基于压缩感知算法的重构方法

2006年以来，压缩感知逐渐兴起并成为一种极具吸引力的信息采集理论，这种新的信号压缩传感理论，能够突破传统Nyquist采样定理极限，获得较高信号恢复质量的同时，极大地减少了采样次数[25]。 2009 年，Katz 等[26]首次将压缩感知方法应用于鬼成像待测物体的重构，在获得高质量成像的条件下，极大地减少了鬼成像系统中所需的测量次数。2010年，Liu等[51]基于压缩感知框架，提出了高质量的量子成像优化算法。中国科学院上海光机所韩申生研究小组分析了不同稀疏方法对鬼成像质量的影响，并提出稀疏约束下的关联成像雷达方案[52-53]。笔者研究小组也结合压缩感知重构方法，提出一些鬼成像改进方案[27-28，54]。

由压缩感知理论可知，它的基本过程表现为信号的稀疏表示、观测和重构3个方面，其具体步骤如下：

（1）设x是一个N维K稀疏的（K≪N）或是可压缩（即通过某种变换可成为K稀疏）的信号，可以得到信号x的稀疏表示

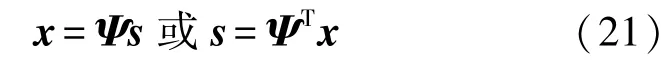
其中，Ψ是大小为N×N的正交的稀疏变换矩阵，s为N×1维K稀疏变换系数。

（2）为了保证稀疏向量s从N维降到M维的过程中重要信息不遭破坏，设计一个平稳的、与稀疏变换基Ψ不相关的M×N（M＜N）维的观测矩阵Φ，对信号x进行测量，得到向量y

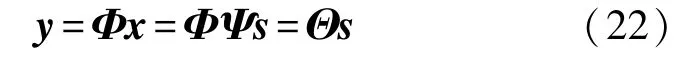
（3）设计一种快速重构算法，从线性观测y＝Φx中恢复信号，其实就是0-范数意义下的优化问题的精确求解或近似逼近值＾，表示为

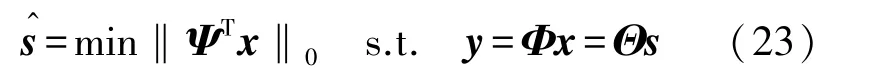
（4）将再作稀疏逆变换，得到原信号x的近似解＾。

若待测物体是可稀疏化的，将鬼成像中桶探测器值构成的向量看作是观测向量，N次散斑构成矩阵看作是观测矩阵，在散斑矩阵与待测物体不相关条件下，可以基于压缩感知算法重构出待测物体。因为基于压缩感知的重构方法，要求散斑矩阵与待测物体不相关，因此，此时散斑常采用随机散斑，如高斯随机散斑或伯努利分布散斑，且在相同稀疏基和测量矩阵条件下，不同的压缩感知重构算法获取的恢复图像质量并不相同[54]。图3是高斯随机散斑下基于增广拉格朗日法和交替方向法的全变分最小化算法（TVAL3）、正交匹配追踪算法（OMP）、压缩采样匹配追踪算法（CoSaMP）和梯度投影算法（GPSR_Basic）对鬼成像质量的影响。以均方误差（MSE）、峰值信噪比（PSNR）、匹配度（MR）和结构相似性指标（SSIM）等作为成像质量客观评价标准。研究结果表明，在压缩比为0.5时，TVAL3算法还原度最高，CoSaMP算法重建图像失真最为严重，且GPSR_Basic算法获得的重建性能要优于OMP算法。

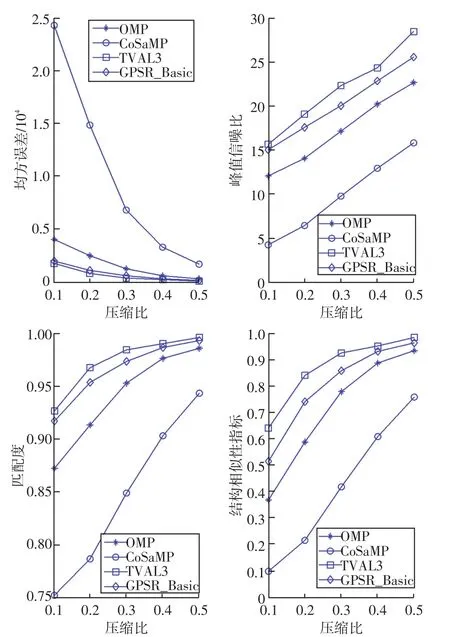
图3 不同压缩比下4种压缩感知重建算法对鬼成像重构的影响[52]

基于压缩感知算法的重构方法存在一些缺点：（1）重构算法较复杂，特别是在实现大像素的待测物体成像时，时间太长，甚至有时无法计算出结果；（2）无法克服背景光的干扰，这意味着当背景光也同时被探测器接收时，噪声信号的增加会导致信噪比降低，甚至淹没信号，极大地限制了鬼成像技术的应用。

2.2.3 基于傅里叶逆变换的重构方法

针对正弦或余弦散斑，暨南大学钟金钢研究小组于2015年提出了一种基于傅里叶逆变换的重构方法[30]，其中，鬼成像中桶探测器值获取过程被看作是获取待测物体的频谱过程，则可通过傅里叶逆变换重构待测物体。

若鬼成像中使用了正弦散斑，其数学形式为式（5），若为桶探测器则值是式（6），与待测物体信息的频谱有关。若考虑桶探测器在实验中将受到背景光的干扰，此时桶探测器的测量值可改为

从特朗普推特看新媒体对美国民粹主义政治生态的影响 ………………………………………… 章瀚夫（6.58）

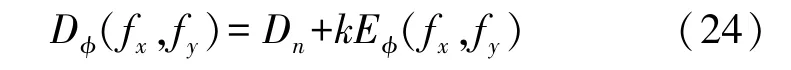
其中，k为比例因子，其值由探测器的探测面尺寸和位置决定，Dn表示探测器对背景光的响应。若对待测物体在相同空间坐标（x，y）和空间频率坐标（fx，fy）下，在不同初始相位（例如，φ＝0，π／2，π，3π／2）上连续测量4次，通过对桶探测器值处理，可以获得该空间频率坐标的待测物体频谱信息，表现为

其中，j为虚部单位。于是，通过傅里叶逆变换，可以获得正弦散斑下待测物体的信息为

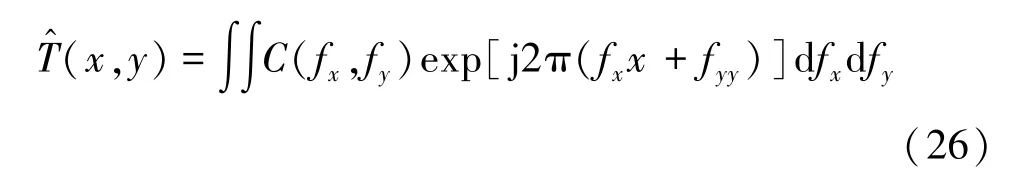
由于在该过程中采用了4个不同初始相位，因此该方法被称为四步相移。另外，在上述获取空间频谱时，可根据图像物体在傅里叶基下的稀疏性，即图像物体频谱的能量集中在中间的低频部分，可以仅设计部分的傅里叶变换矩阵，这样就会极大减少测量次数和照射待测物体的数量。

同样，若假设初始相位取值φ＝ 0，2π／3，4π／3，则可推导出

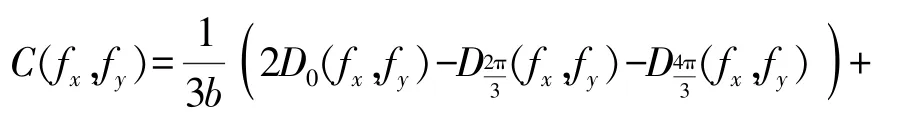
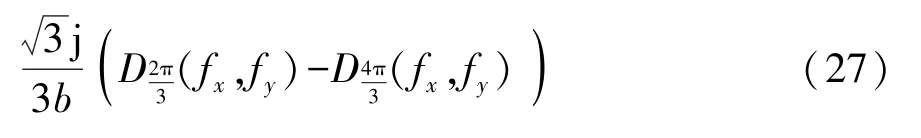
通过傅里叶逆变换可以获得正弦散斑下待测物体的信息。由于在过程中采用了3个不同初始相位，因此此种方法被称为三步相移。

在以上重构中，由于在计算中直流分量a和背景噪声Dn已通过差分测量方法去除，因此基于傅里叶逆变换的重构方法具有较好的抗环境噪声能力。图4是基于傅里叶逆变换四步相移和三步相移下的鬼成像结果。从图4中可知，四步相移与三步相移下鬼成像质量基本相同。

图4 基于傅里叶逆变换四步相移和三步相移重构[55]

2.2.4 基于矩阵运算的重构方法

2014年，郭树旭研究小组将伪逆概念引入鬼成像，提出基于矩阵伪逆的鬼成像重构方法，称为伪逆鬼成像（Pseudo-inverse Ghost Imaging，PGI）[56]。 由式（20）可知，待测物体重构信息可以进一步表示为

结合式（1）和式（2），得到

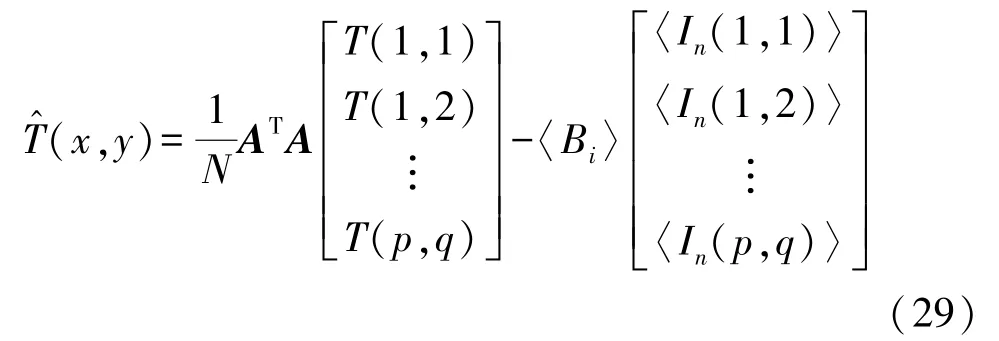
在此基础上，龚文林研究小组提出了一种高分辨率伪逆鬼成像[57]。 Yang 等[58]于 2016 年提出了基于标量矩阵的重构算法（Scalar-Matrix-Structured Ghost Imaging，SMGI）。 2018 年，基于奇异值分解的关联成像算法（Singular Value Decomposition Ghost Imaging，SVDGI）[59]和基于施密特正交化的关联成像算法（Schmidt Ghost Imaging，SGI）[60]也被提出。2018年郭树旭研究小组结合迭代去噪和伪逆鬼成像，提出了鬼成像的伪逆迭代方法，并通过实验验证了方法的有效性[61]。

2.2.5 基于机器学习的重构方法

深度学习是一种用于数据建模、数据分类和决策的机器学习方法，现已成为人工智能领域的研究热点，在图像识别、语音识别、自然语言处理、搜索推荐等领域展现出巨大的优势[62-63]。与此同时，深度学习技术也引起了国内外光学成像研究者的广泛关注。鉴于深度学习可以极大地提高散射成像、相位成像的成像质量，2017年，中国科学院上海光机所司徒国海研究小组将深度学习引入计算鬼成像，用深度神经网络学习模糊图像清晰化过程，并将低测量次数下的鬼成像实验结果输入到训练好的网络中，获得了实验采集时间少、成像质量高的鬼成像[64]。 2018 年，Shimobaba 等[65]也将深度学习应用到计算鬼成像，用深度学习网络训练鬼成像实验噪声，从而有效地改善鬼成像的成像质量。2018年，Higham等[66]使用深度学习模型实现实时视频鬼成像。2019年，司徒国海研究小组实现端到端神经网络的桶探测器值直接对目标物体的重构方法[67]。

2．3 系统优化

通过散斑照射获得一系列桶探测器值和光强分布，再通过重构方法就可以在参考支路上获得待测物体的像。然而，由于热光鬼成像在理论上存在噪声项，其成像质量不可避免地受到限制，再加上实验环境中还存在其他照射源或噪声，因此，很多新的系统优化方法被开发，例如差分鬼成像（Differential Ghost Imaging，DGI）、归一鬼成像（Normalized Ghost Imaging，NGI）和对应鬼成像（Correspondance Ghost Imaging，CGI）等，以期望凭借较少的测量次数和降噪手段，获得成像时间少、质量高的系统优化方法。

2.3.1 差分鬼成像

差分鬼成像是由Ferri等[21]于2010年提出的系统优化方法，通过对信号光路的信号与参考光路的信号做差分处理，使得鬼成像的成像信噪比得到了明显的提高。差分鬼成像的强度关联公式为

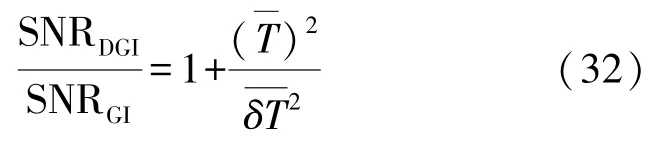
其中，为待测物体平均透射率为其方差。

由于差分运算能够有效抑制背景噪声，提取物体信息相对波动值，因此对于强透射型物体（透射函数满足的成像，差分鬼成像的成像SNR比传统鬼成像有较大程度的提高；而对强吸收型物体（透射函数满足的成像，成像SNR虽仍有所提高，但提高程度很不明显。

笔者研究小组在差分鬼成像的基础上结合压缩感知技术，提出了基于压缩感知的差分关联成像方案[27]、参考臂差分压缩关联成像[68]以及多散斑图的差分压缩鬼成像方案[69]，有效地提升了鬼成像的成像质量并减少了测量次数。

2.3.2 归一鬼成像

归一鬼成像同样也是对信号光路与参考光路的信号做一定的数据处理，优化鬼成像系统[22]。通过归一化处理得到的成像信噪比与差分鬼成像几乎相同，即归一鬼成像也同样可以提升鬼成像的图像质量，只不过是数据处理方法跟差分鬼成像有些不同。

归一鬼成像的强度关联公式如下

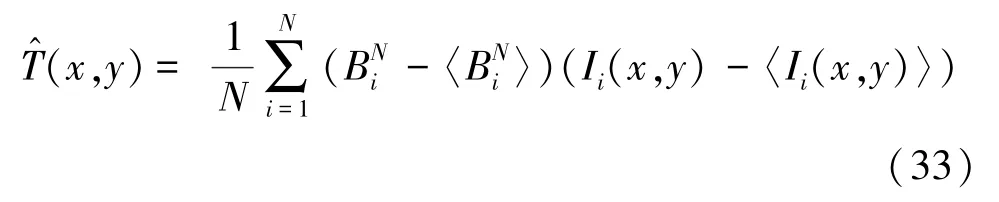
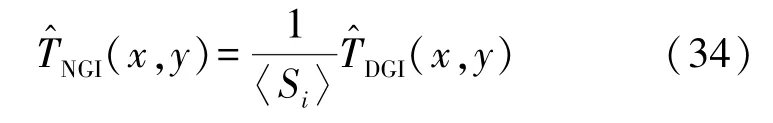
因此，归一鬼成像的信噪比与差分鬼成像的信噪比相同，即

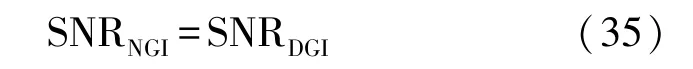
这说明归一鬼成像可以得到和差分鬼成像一样的重构鬼成像质量。

2.3.3 对应鬼成像

对应鬼成像因为不需要传统鬼成像所需要的强度关联运算，所以这种方式极大地简化了运算，节省了计算时间[39]。假设在鬼成像实验过程中总共记录了N个探测器的测量值Bi，记为B1，B2，…，BN和N个散斑Ii（x，y），记为I1（x，y），I2（x，y），…，IN（x，y）。然后将各个Bi与〈Bi〉相比，如果Bi大于〈Bi〉，对应的散斑记为；如果Bi小于〈Bi〉，对应的散斑记为。 对应鬼成像的成像公式如下

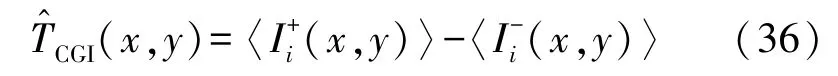
虽然式（36）看起来重构方法仅与散斑有关，而与桶探测器的测量值无关，但是事实并不是如此。因为需要使用桶探测器的测量值作为判断的依据，由它对散斑进行分组，分为正对应散斑光场强度和负对应散斑光场强度，然后再由它们两个的差值得出重构鬼成像图像。

笔者研究小组结合对应鬼成像、归一鬼成像和压缩感知技术，提出了对应归一化压缩鬼成像[28]，显著提升了鬼成像的成像质量。还进一步将对应鬼成像和压缩感知技术应用到高阶鬼成像中，提出高阶差值筛选鬼成像方案[70]，提升了高阶鬼成像的成像质量。

3 鬼成像技术应用

鬼成像自1995年被实验证实以来，已经被广泛应用于激光雷达探测、3D成像、光信息加密以及边缘检测等领域。下面就鬼成像在光学加密和边缘检测方面的应用进行简单综述。

3．1 光学加密

2010年，Clemente等[71]提出了基于计算鬼成像的光学加密方法。实验中，以加载到空间光调制器上的散斑图信息为密钥，以目标物体的测量值为密文，接收方收到密文后，结合密钥进行解密。2012年，Tanha等[72]提出基于计算鬼成像的灰度和彩色方法。在此基础上，Zafari等[73]于2014年提出了基于选择性计算鬼成像的光学加密方法，提高了光学加密的安全性。笔者研究小组于2015年提出了基于计算鬼成像的使用QR编码和压缩感知技术的高性能光学加密方案[74]，此后，还提出了一种基于计算鬼成像的图像隐藏方案，以随机散斑构成密钥，实现最低有效位的数字水印方法[20]。图5描述了基于计算鬼成像的图像隐藏方法，其中，图5（a）描述了获取水印过程，图5（b）描述了水印加载过程，图5（c）描述了水印提取过程。

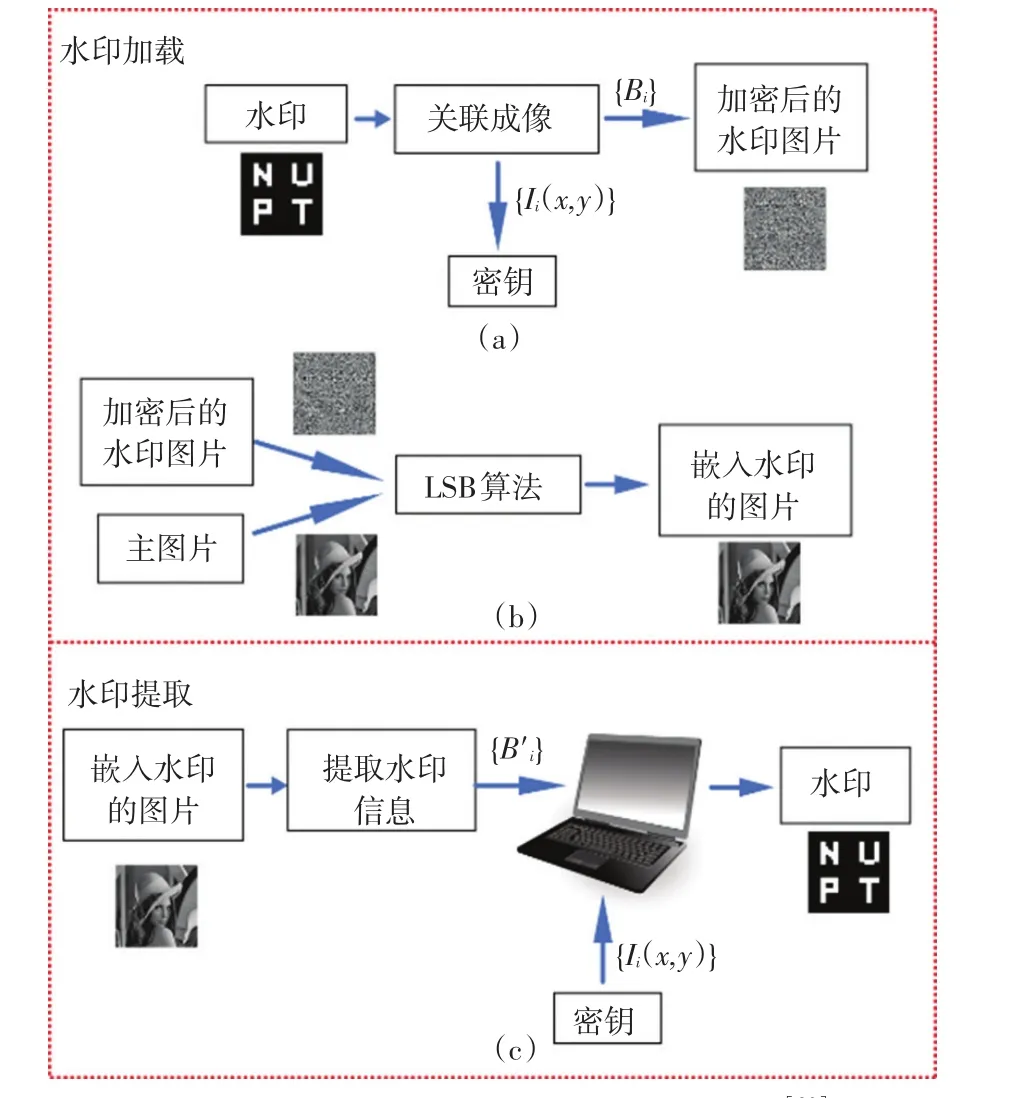
图5 基于计算鬼成像的图像隐藏方案[20]

利用计算鬼成像系统，将水印T（x，y）作为待测物体，随机散斑Ii（x，y）为密钥，可以在合法用户间共享桶探测结果Bi，即加密后的水印图片。由于桶探测结果Bi是一个十进制实数，可以通过IEEE754标准将其转换为32位的二进制浮点数，其中，第1位为符号位，随后8位表示指数，最后23位表示分数。于是，N次桶探测结果可以表示为32×N位二进制数，顺序排列后可构成一个32×N像素的二值灰度加密后的水印图片，其中每一个像素的灰度值等于对应的比特值。采用LSB算法将需要加载的信息隐藏在主图片的最小位置。在提取水印过程中，先使用LSB算法将加密后的水印信息从嵌入水印的图片中提取出来，获得隐藏在第8位的加密后的水印图片，即获得N个32位的二进制浮点数。最终授权用户可以通过二阶相关运算和压缩感知算法对水印进行提取，恢复出水印T（x，y）。研究结果表明，当窃听率低于45%时，该方法可以保证窃听者无法有效地获取水印信息。

随后，笔者研究小组还提出了无序散斑鬼成像光斑加密，基于Toeplitz矩阵和轴向距离的双密钥光学加密以及基于多波长光源的光学加密等[75-77]，有效地提升光学加密的安全性和有效性。

3．2 边缘检测

2015年，Liu等[78]将梯度算子引入鬼成像，提出梯度鬼成像（Gradient Ghost Imaging，GGI），实现对未知目标物体的边缘检测，为非定域地提取目标信息提供了一种新颖的思路。2016年，Mao等[43]提出基于Sobel算子的鬼成像边缘检测方法（Speckle-Shifting Ghost Imaging，SSGI），克服了梯度算子的缺陷，提升了目标物体边缘检测质量。2018年，Yuan等[79]提出一种基于结构照明的计算鬼成像方法，同年，笔者研究小组将亚像素引入鬼成像边缘检测中，提出一种基于亚像素移动散斑关联成像的边缘检测方案[80]和基于频域单像素的边缘检测方案[81]。2020年，Chen等[82]提出了基于 Kirsch算子的多向边缘检测方案。笔者研究小组也提出了一种基于可变尺寸Sobel算子的鬼成像边缘检测方法[83]，即使在严重噪声的环境下，该方法也能获得更清晰、更连续的边缘；同时，将压缩感知算法引入基于梯度算子和Sobel算子的边缘检测中，进一步降低边缘提取所需要的测量次数[84]。图6是基于频域单像素的边缘检测的仿真结果和实验结果，第一列是二值目标物体，包括英文字母’NUPT’、中文汉字‘中‘等，第二列是Sobel算子作用下边缘检测结果，第三列是使用笔者研究小组所提方法结果。从结果可以看出，对未知待测物体，通过所提方法能够得到待测物体较为清晰的边缘信息，从而证实了所提方法进行边缘检测的可行性。

图6 基于频域单像素的边缘检测的仿真结果和实验结果[81]

4 结束语

鬼成像技术作为一种新型的成像技术，能够在不可达环境下对待测物体（目标物体）进行成像，有效地将信号获取的压力从采样端转移到接收端，且具有抗干扰能力强的特点，在雷达探测、3D成像、运动物体检测、光学加密、边缘检测等方面具有巨大的应用前景。本文从鬼成像的研究历程出发，结合鬼成像的基本原理，分析了影响鬼成像质量的若干因素，综述了鬼成像在散斑结构与产生、重构方法和系统优化方面的研究进展，并进一步展示了鬼成像技术在光学加密与边缘检测方面的研究成果。目前，鬼成像技术仍需要进一步地研究与完善，其作为量子光学研究热点之一，充满着机遇与挑战。