横轴式截割减速器动载特性的灵敏度分析*
孟祥军, 尹明虎, 李祥千, 孙飞飞, 刘豪
(1. 兖矿集团有限公司, 山东 济宁 272000;2. 兖矿集团博士后科研工作站, 山东 济宁 272000;3. 西安理工大学 机械与精密仪器工程学院, 陕西 西安 710048;4. 兖州煤业股份有限公司 设备管理中心, 山东 济宁 272000; 5. 方圆集团有限公司, 山东 烟台 264000)
0 引言
悬臂式掘进机是我国煤矿巷道掘进的主力机械,高效机械化掘进技术是保证矿井高产高效的必要条件[1]。悬臂式掘进机可分为纵轴式和横轴式两种,其中横轴式掘进机因截割硬度高、稳定性好等优点成为现今掘进行业的主流研究方向[2]。在掘进机中,截割减速器位于截割头和截割电动机之间,其工作性能对掘进机截割能力有直接影响[3]。横轴式掘进机截割减速器(以下称横轴式截割减速器)在工作时,其内部的齿轮传动系统存在振动和噪声,这会对工作部件产生不利影响[4-5]。因此,进行动态条件下的齿轮传动系统振动特性分析是提升横轴式截割减速器设计质量的重要工作之一。
鉴于此,本文以某横轴式截割减速器齿轮传动系统为例,首先建立其ADAMS虚拟样机模型,然后运用多元线性回归与正交试验设计等理论及技术,进行齿轮传动系统结构参数对动载特性的灵敏度分析,分析结果可以为横轴式截割减速器设计及分析提供理论及技术参考。
1 几何模型
给定的设计要求为输入功率320 kW,输入、输出转速分别为1 470、 21 r/min,在完成了横轴式截割减速器齿轮传动系统设计之后,利用SolidWorks软件对其进行三维建模、虚拟装配及干涉分析,以保证后续工作的开展。图1和表1分别给出了设计完成的三维模型及各级齿轮传动主要结构参数。

1-第Ⅰ级斜齿轮传动;2-第Ⅳ级行星齿轮传动;3-第Ⅲ级行星齿轮转动;4-第Ⅱ级锥齿轮传动。

表1 各级齿轮传动的主要参数
研究使用的齿轮传动系统第I、II级分别为斜齿轮、锥齿轮传动,第III、IV级为行星齿轮传动(采用对称布置的形式)。表1中下标1、2表示齿轮传动的主/从动轮,下标s、p、r分别表示行星齿轮传动中的太阳轮、行星轮和内齿圈。
2 虚拟样机模型
为获得横轴式截割减速器齿轮传动系统运行过程中的动载特性,本文基于ADAMS进行其动力学仿真。
2.1 模型简化及设置
横轴式截割减速器齿轮传动系统的三维模型十分复杂,为减少仿真分析的时间成本,对三维模型进行了如下简化:
1) 考虑到左右对称布置的行星齿轮传动结构参数完全相同,故仅保留一侧。
2) 省略垫片、挡圈等仅起轴向定位作用的零件,忽略键槽、倒角等特征。
3) 将轴颈处以弹簧-阻尼器的形式设置支承刚度。
将简化处理后的传动系统三维模型导入ADAMS中,并进行材料定义(如表2所示)、约束添加、驱动及负载设置、碰撞力参数定义等操作。

表2 各齿轮材料
1) 斜齿轮、锥齿轮与机架之间添加旋转约束,两级行星齿轮传动的内齿圈及太阳轮与机架之间添加旋转约束。
2) 在第Ⅰ级斜齿轮传动上添加输入转速。
3) 静态负载转矩施加在第Ⅰ级传动的主动轮旋转副上。
4) 由齿轮传动的工作特点,以基于刚度和阻尼系数的Impact碰撞接触力模型模拟齿轮传动工作过程中的轮齿啮合力,其表达式为:
(1)
式中,q0为两接触物体的初始距离;l为两接触物体的实际距离;e为刚性力指数,对于金属与金属之间的碰撞接触,其取值为1.5;d为碰撞渗透深度,一般取0.1 mm;C为阻尼系数,一般取刚度系数K的0.01%;刚度系数K的计算公式为:
(2)
式中,R为综合曲率半径,E为综合弹性模量。
5) 使用库伦摩擦力模型定义齿轮副之间的摩擦力,对于润滑良好的金属表面,取其静摩擦因数为0.1,动摩擦因数为0.08。
在进行了以上处理之后,建立的虚拟样机模型如图2所示。

图2 齿轮传动系统仿真模型
2.2 模型求解
在ADAMS虚拟样机分析软件中,利用带拉格朗日乘子的第一类拉格朗日方程的能量形式得到如下方程:
(3)

ADAMS中使用WSTIFF积分器及SI2格式开展系统仿真分析。
2.3 仿真结果及模型验证
对建立的ADAMS虚拟样机模型进行系统初步设计方案的动力学仿真。图3给出了仿真获得第III级行星齿轮传动的输出转速、太阳轮与行星轮的动态啮合力(为便于观察,动态啮合力只给出达到稳态后的结果)。可以看出,施加载荷0.2 s后,输出转速和太阳轮与行星轮之间的动态啮合力的仿真分析结果呈周期性变化,这与动态条件下齿轮传动的工作状态相符。
为对虚拟样机模型合理性及可靠性进行进一步验证,有必要进行静态条件下系统各级齿轮传动的传动比及啮合力计算。根据机械设计手册中相关理论,将得到的传动比与啮合力的理论计算结果与仿真结果进行对比,结果如表3、表4所示(因行星轮存在功率分流特性,故各行星轮与太阳轮/内齿圈的啮合力差距小,所以表中仅列出一组仿真结果)。从表3、4可以看出,各级齿轮传动传动比的理论值与仿真值之误差均不超过1%,啮合力的仿真值与理论值之间的误差不超过3.2%,表明本文建立的横轴式截割减速器齿轮传动系统虚拟样机模型具有较高的可靠性。

(a) 输出转速

表3 传动比的理论计算结果与仿真结果的对比

表4 啮合力的理论计算与仿真的结果对比
3 灵敏度分析
在齿轮传动系统动力学研究中,动态载荷是体现齿轮传动系统动力学特性的重要性能指标。将表征系统动载特性的综合最大动载系数为指标,分析该齿轮传动系统的动载特性对齿轮结构参数之灵敏度。综合最大动载系数的计算公式为:
(4)
式中,KD为各级齿轮传动的最大动载系数;KDI表示第III、IV级行星齿轮传动太阳轮与行星轮啮合的最大动载系数;KDO表示第III、IV级行星齿轮传动行星轮与内齿圈啮合的最大动载系数;KS为系统综合最大动载系数,其值为各齿轮传动最大动载系数的平均值;Fmax为仿真获得的各级齿轮传动动态啮合力的最大值;FT为各级齿轮传动啮合力的理论计算值;上标j表示齿轮传动级数。
根据设计要求,在保证各级齿轮传动比不变的情况下,分析横轴式截割减速器齿轮传动系统的动载特性对齿轮结构参数的灵敏度。根据相关手册可知,齿轮模数、齿宽系数和压力角对齿轮的工作有较大影响,另外由于所研究的齿轮传动系统输入齿轮为斜齿轮,故将其螺旋角加入到灵敏度分析中(根据设计要求,各级齿轮传动的齿宽系数和压力角取值相同),各参数的取值范围如表5所示。

表5 灵敏度分析中的齿轮结构参数
为确定各结构参数对系统动载特性的影响程度,首先进行影响程度分析,其结果如图4~图7所示(图5~图7中标识同图4)。图4(a)~(d)说明:4级中的任一级齿轮模数发生变化时,除引起本级系统动载系数变化外,还会引起其他3级动载系数和系统综合动载系数的变化。综合来看:各级齿轮模数对系统动载特性的影响最明显,但齿宽系数、压力角及斜齿轮传动螺旋角的影响程度难以通过影响程度分析的结果得出。继而以齿宽系数、压力角和第Ⅰ级齿轮螺旋角为对象,基于多元线性回归分析,开展系统动载特性对上述参数的灵敏度分析,以量化三者对系统动载特性的影响程度。
灵敏度分析须以一定数量的数据样本为支撑,本文采用正交试验设计方法获得了灵敏度分析所需的20组少量样本数据,并借助前述建立的虚拟样机模型进行了这些参数组合下的系统动力学仿真,获得了相应系统最大动载系数的仿真结果,限于篇幅,表6列举了5组样本及其最大动载系数的仿真结果。
多元线性回归分析是研究一个变量与多个自变量之间变动规律的统计方法[6]。设目标变量为y,设计变量为x1、x2、x3,其多元线性回归数学模型为:
y=β0+β1x1+β2x2+β3x3
(5)
式中,β0、β1、β2、β3称为回归系数。

(a) 第Ⅰ级齿轮模数对动载系数的影响

图5 齿宽系数对系统动载特性的影响

图6 压力角对系统动载特性的影响

图7 第I级齿轮螺旋角对系统动载特性的影响
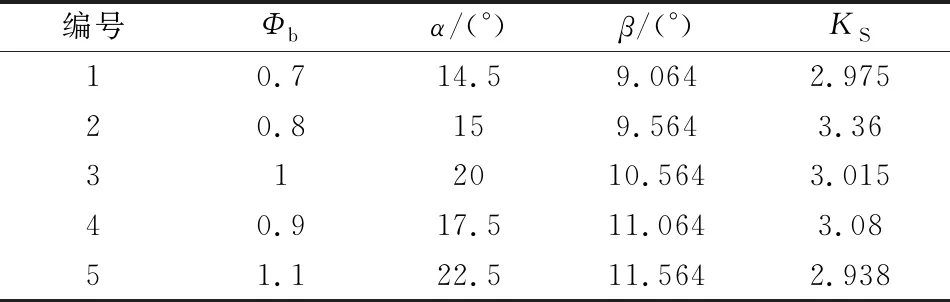
表6 若干灵敏度分析样本数据
以式(5)进行n次(对本文而言n=20)独立计算,则有:
(6)
将式(6)写作矩阵形式:
Y=xβ
(7)
式中,
(8)
各回归系数的值可由最小二乘法进行估计:
(9)
回归分析完成后,须用回归模型及参数进行统计检验,常用的检验方法有R和F检验。
R检验一般用于检验回归模型的拟合优度,其计算公式为:
(10)

F检验用于检验回归系数的显著度,其计算公式为
(11)
式中,m为自变量个数。
基于上述模型,对不同结构参数下的系统综合最大动载系数仿真结果进行多元线性回归分析,求解可得:
1) 回归系数。β=[5.092,7.060,-0.228,-0.414],其线性回归方程为:
y=5.091 5+7.06x1-0.228x2-0.414β3x3
(12)
2)R检验中。R=0.9998,其值接近于1,表明回归模型拟合优度良好。
3)F检验中。F=157.76,与之对应的概率P=0.018 5。取显著水平值a=0.05,查F分布表可得F0.05(3,16)=3.24,通过对比可知该模型的回归效果显著。
比较式(12)中各参数的回归系数,可知齿宽系数对系统动载特性的影响比压力角和斜齿轮螺旋角大。所以,对横轴式截割减速器齿轮传动系统动载特性影响程度的排序为:各级齿轮模数>齿宽系数>压力角>第Ⅰ级齿轮传动螺旋角。
4 结论
以在ADAMS中建立的某横轴式截割减速器齿轮传动系统之虚拟样机模型为基础,结合正交试验设计及多元线性回归分析,进行了齿轮结构参数对系统动载特性的灵敏度分析。
在本文研究范围内,得出各级齿轮模数及齿宽系数对系统动载特性影响较为显著,压力角和第I级斜齿轮螺旋角对系统动载特性影响较小。分析方法和相关分析结果为横轴式截割减速器分析及设计提供一定参考。

