网络信息体系弹性影响因素重要性评估方法*

冉淏丹，张 彬，王 哲，毕俊菲

（国防科技大学信息通信学院，西安 710106）

0 引言

网络信息体系是以“网络中心战”［1］思想为重要理论，按照“信息主导，网络赋能，体系聚能”的总体思路，依托栅格化物理基础网，链接地域分布广泛、运行管理相对独立的情报系统、指控系统、武器系统、保障系统等组分系统建立起来的能够支撑联合作战体系能力生成与发挥的复杂信息体系［2］。

目前，针对网络信息体系的研究主要包括基本概念与制胜机理［3］，体系结构［4］与能力发展规律［5］，运作机理与关键技术［6］，体系复杂性［7］等方面，对网络信息体系弹性及其影响因素的分析研究较少。弹性是网络信息体系的一种潜在的涌现型特征［8］，也是衡量网络信息体系面对战场威胁攻击时适应性和恢复性的重要指标。因此，探析网络信息体系弹性作用机理，找出影响体系生成与发挥的重要因素，对优化网络信息体系结构，提升体系生存能力具有重要作用［9］。

本文从分析网络信息体系弹性作用过程入手，提炼影响体系弹性的主要因素，基于熵理论和群决策理论［10-12］，聚合熵权和偏离度确定专家决策权重，设计了一种基于偏离度的权重调整算法，对专家决策权重进行调整，直到决策结果趋于稳定一致，并通过等级映射的方法对决策结果进行评价，最终得到较为客观准确的网络信息体系弹性影响因素的重要性评估结果。

1 体系弹性的影响因素分析

在复杂未知的对抗环境中，网络信息体系面临持续性威胁攻击的风险，其弹性表现为系统能够准确预测风险波及范围，主动承担威胁攻击，及时吸收系统扰动，维持系统低功率运行，并且在可接受时间内恢复其功能状态的能力。从网络信息体系组成来看，其弹性来源主要包括以下两个方面：一是网络化结构演化所涌现出的网络弹性［13］，主要表现为信息网络在攻击或故障情况下，网络承载能力面临降级威胁时，网络通过负载吸收、功能恢复，以及形态重塑的多种策略形成的快速应变能力；另一方面，网络信息体系组分系统单元本身具备的性能维护、功能升级、攻击免疫等多种弹性策略，在一定程度上决定着网络信息体系的弹性化程度［14］。

由此可见，网络信息体系弹性来源于体系的动态演化过程，与体系对抗过程紧密相关，是具有阶段性和整体性特征的复杂属性。综合考虑体系对抗和网络信息体系特点，可将体系弹性作用过程分解为风险预测、威胁响应、攻击承受和恢复重建4 个阶段，通过体系能力E（s）的变化来描述体系弹性过程，如图1 所示。

风险预测阶段。风险是指具有一定概率导致网络信息体系性能降级的攻击事件。弹性的网络信息体系必须具备一定的风险预测能力。网络信息体系组成要素中包含多属性的具有态势感知功能的单元，多个单元之间的精准协同影响战场态势信息，针对具体态势信息进行准确判断，多种信息融合交互并形成决策。因此，考虑到风险预测的时效性、准确性和完备性，提炼出风险预测阶段体系弹性的重要影响因素主要包括：感知单元协同、态势信息判断、信息交互反馈3 类。

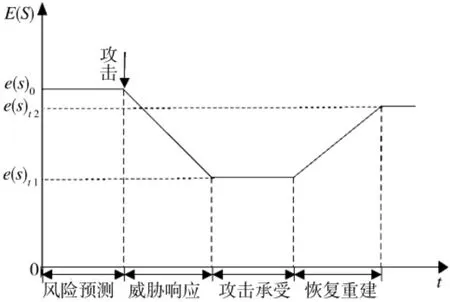
图1 网络信息体系弹性过程

威胁响应阶段。威胁是已造成网络信息体系性能降级后果的攻击事件。识别和响应威胁是网络信息体系面对突发攻击，采取措施积极应对的基本手段。威胁识别精度决定攻击事件的发现概率和准确度，影响后续信息分析处理结果；正确判断威胁形势、选择响应策略，在一定程度上决定威胁响应效率；体系内部要素的联动机制决定信息流转机制，影响各要素之间信息交互、综合决策、行动协同效率。因此，威胁响应阶段影响体系弹性的主要因素包括识别精度、响应策略、要素联动机制3 类。

攻击承受阶段。攻击承受阶段弹性表征网络信息体系面对外界软/ 硬攻击时所表现出的生存能力。赛博攻击可能会体系内部网络流量激增，单元负载过重失效，引发网络大面积瘫痪，功能降级失效；物理攻击旨在摧毁实体要素，影响体系各功能要素正常运转，使得网络信息体系对作战任务的完成程度减弱，一旦突破任务能力阈值，体系弹性将发生断崖式下降。此外，攻击强度、类型和位置的不同，都会对体系生存产生不同影响效果，例如针对核心要素和重点部位展开高强度攻击对体系产生的降级威胁更大。从组织实施层面考虑，决策者通过态势判断并结合以往经验下达指令，选择合适的战术战法应对攻击事件，能够减少体系力量整体降级程度，发挥最大战斗力。因此，在这一阶段网络信息体系弹性主要受攻击位置、攻击强度、任务能力阈值、战术战法选择等因素的影响较为明显。

恢复重组阶段。弹性的网络信息体系一个明显的特征就是在毁伤后能够进行恢复重组和能力再生。从结构层面看，网络信息体系组成成分复杂，构成体系的各网系要素功能损毁程度，直接关系到体系能力降级程度。受损部分结构复杂度会影响结构恢复时间和功能恢复程度；从决策层面看，修复策略的选择决定了功能恢复的优先级，也会对体系整体能力再生产生影响；从技术层面看，修复科技的先进与否会对网系要素功能接替和体系结构的重构产生重要影响。因此，将该阶段弹性的影响因素提炼为结构复杂度、优先级选择和技术水平。

综合上述分析，网络信息体系弹性影响因素如图2 所示。

2 基于熵理论群决策的影响因素重要性评估

2.1 问题描述

由于影响网络信息体系弹性的因素涉及类型广泛，很难通过收集大量可靠样本数据进行统计分析，进而量化其影响因素的重要性。相比而言，领域专家决策可以作为一种近似可行的评估方法。本文借鉴熵理论和群决策相关理论，在获得领域专家初始权重的基础上，运用权重偏离度和熵权思想不断对领域专家决策权重进行调整，直到决策结果趋于稳定一致。

若直接由上述思路得出评估结果较为简单，且其量化计算未考虑到各领域专家的决策结果和最终评估结果的一致性，即Wk与X 往往存在偏差，偏差越大说明该专家对弹性影响因素重要性排序提供的信息量越大，则对其决策权重的调整不能过小；偏差越小说明该专家对评估结果提供的信息量越小，因此，在实际决策过程中该偏差对决策结果的影响不能够忽略。为尽可能得到更为客观准确的决策结果，需要尽可能地使得两类结果趋于一致，可以通过对专家的决策权重进行调整来实现。因此，本文引入熵理论，衡量各领域专家的信息量对进行客观设定，通过判定偏离程度对进行调整，有助于得到更为科学的评估结果。

2.2 熵权计算

根据上述熵的计算公式可知，当个体专家决策结果越接近，其熵值越大，与群决策结果的一致性越高，但对群决策结果的影响也越小，因此，赋予其较小权重；反之，专家熵值越大，对最终评估结果的信息量贡献值越大，应增加其权重。因此，通过系统熵确定专家决策权重的熵权部分具有合理性。

2.3 偏离权重计算

2.4 权重调整

3 影响因素重要性等级映射

网络信息体系弹性影响因素重要性等级是在定量计算的基础上，为进一步判定影响因素重要性，反映体系弹性影响因素之间的重要程度的区间化描述。由上文可知，网络信息体系弹性影响因素个数为n=13，将其重要程度从高到低设置为A、B、C、D、E 5 个等级，网络信息体系弹性影响因素权重值与重要性等级的映射关系如表1 所示。

表1 影响因素重要性等级映射表

4 算例分析

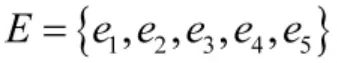
步骤1 依据表2 中数据，由式（1）计算得到5位专家未达成决策一致时的13 项影响因素重要性系数综合决策结果X=（0.145，0.032，0.164，0.043，0.007，0.131，0.071，0.074，0.105，0.055，0.104，0.056，0.15）。

步骤2 求熵权。依据表2 中数据，结合式（3）、～式（5）计算得到专家决策权熵权结果。

步骤3 求偏离权重。依据表2 中数据，结合式（6）、式（7）计算得到5 位专家决策权重的偏离权重初值。

表2 网络信息体系弹性影响因素权重初始情况表

表3 专家决策权重初始计算结果表

步骤4 权重调整。依据上述计算结果，综合熵权和偏离权重，由式（8）计算得到首次调整后领域专家决策权重= {0.272，0.144，0.180，0.132，0.272}（α=0.6，β=0.4）。将调整后的权重代入式（9），得到首次调整后影响因素重要性系数综合决策结果：X=（0.047，0.036，0.068，0.043，0.068，0.141，0.067，0.065，0.101，0.053，0.109，0.060，0.143），将其带入式（10），进一步判定：当时，权重调整过程结束，否则重复式（6）～式（9），直到差值降到阈值l 以下，得到最终权重调整结果（本算例中设定l=0.001）。专家决策综合权重的变化过程如表4 所示。

表4 专家决策综合权重变化表

通过调整算法，在熵权和偏离权重的综合影响下，最终专家的决策权重趋于稳定。综合权重调整的变化曲线如图3 所示。

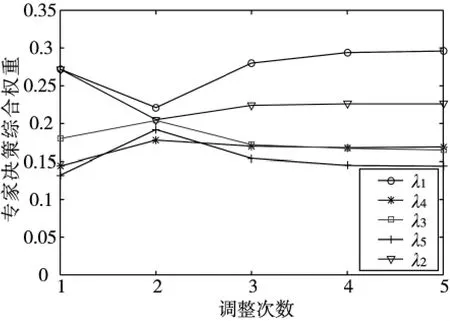
图3 专家决策权重调整变化曲线

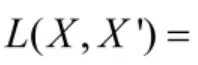
步骤6 影响因素重要性等级映射。将专家群决策结果与表1 中的映射关系对照，得到网络信息体系弹性影响因素重要性等级，结果如下页图4 所示。

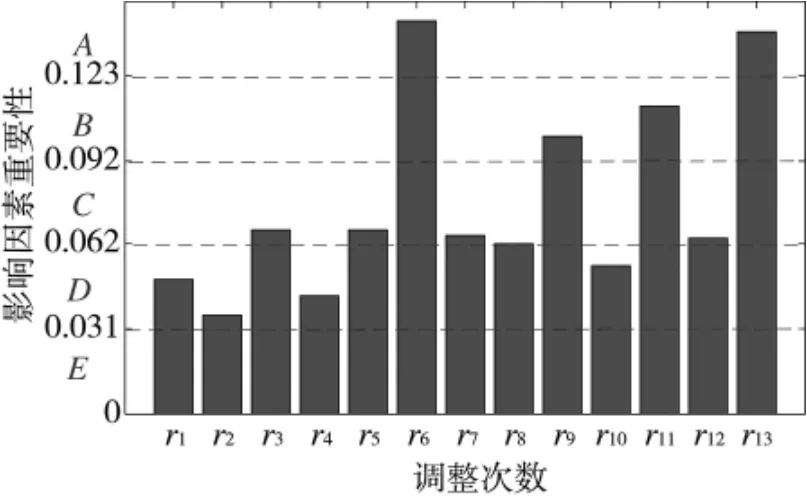
图4 网络信息体系弹性影响因素重要性等级

从上述算例分析可知，对网络信息体系弹性影响的重要因素有：要素联动机制、技术水平、体系结构复杂程度以及任务能力阈值4 种。相对来说，其他影响因素重要性程度较弱，其中，态势信息判断和威胁识别精度重要程度最低。通过本文设计的网络信息体系弹性影响因素重要性评估方法，能够有效整合领域专家决策意见，得到高权威度、客观可行的重要性等级映射结果，从而准确地对影响网络信息体系弹性的因素进行分析，并从中筛选、挖掘出具有较高重要性的关键因素，为后续网络信息体系弹性的优化提供重要参考。

5 结论

从体系弹性的作用过程出发，分别针对风险预测、威胁响应、攻击承受、恢复重建4 个阶段提炼影响体系弹性的因素，在此基础上，结合评估领域相关理论方法，选择基于熵理论群决策评估方法确定网络信息体系弹性影响因素重要性权重，包括熵权理论、群决策理论以及专家决策一致性的权重调整方法等，采用等级评定法确定体系弹性影响因素重要性，设计重要性系数与重要性等级映射关系，最终确定网络信息体系弹性重要性等级。通过算例计算验证了该评估方法的有效性和可行性，能够为实际应用提供一定的参考价值。