果蝇优化算法的进展研究分析

张水平，王丽娜

江西理工大学 信息工程学院，江西 赣州 341000

求解最优化问题一直都是计算机工程、生产调度、人工智能等领域广泛关注的一个问题。近年来，以粒子群算法（PSO）[1]、蚁群算法（ACO）[2]、遗传算法（GA）[3]等为代表的群智能算法为人们求解复杂问题提供了强有力的工具。果蝇优化算法（Fruit Fly Optimization Algorithm，FOA）[4-5]是潘文超博士在2011年提出的一种新型的仿生类元启发式智能优化算法，它是通过模仿自然界中果蝇利用其敏锐的嗅觉和尖锐的视觉的觅食行为而设计的一种演化式计算的新算法。FOA 调节参数较少，操作简单，具有易于构建的代码框架，可塑性强，只要调节好核心参数，就较容易应用于多个领域去解决实际问题。吴小文等[6]和刘立群等[7]将果蝇优化算法与主流群体智能算法的寻优性能进行对比，结果如表1所示。实验结果表明，果蝇优化算法相比于其他群智能算法计算量较小运行时间短，在迭代次数较低时，收敛精度和收敛速度要比其他群智能算法更高更快，因此全局寻优能力很强。以上的各种优势使其一经提出便受到国内外众多学者的关注和研究。在应用上，果蝇优化算法属于一种研究方法，无领域限制，已被应用于多个学科领域[8]。本文总结了果蝇优化算法从提出到现在国内外对其研究的主要成果，包括在候选解产生机制、搜索步长以及飞行策略等方面的改进和在复杂函数优化、参数优化、调度及物流问题等方面的应用，为FOA的推广应用提供有效的资料，最后提出FOA 在算法改进和实际应用方面研究的新方向。

1 标准果蝇优化算法

果蝇广泛地存在于全球温带及热带气候区，相较于其他生物，果蝇具有更发达的嗅觉和视觉，果蝇通过敏锐的嗅觉发现食物源的位置，并分享给其他的果蝇或者接收其他果蝇分享而来的信息，比较得出气味最优的果蝇个体位置，同时利用自身发达的视觉发现食物和同伴聚集的位置向该位置飞去，形成新的果蝇群体中心，如此重复操作，直到找到食物。根据果蝇群体觅食行为特征，标准FOA可大致分为以下几个步骤：

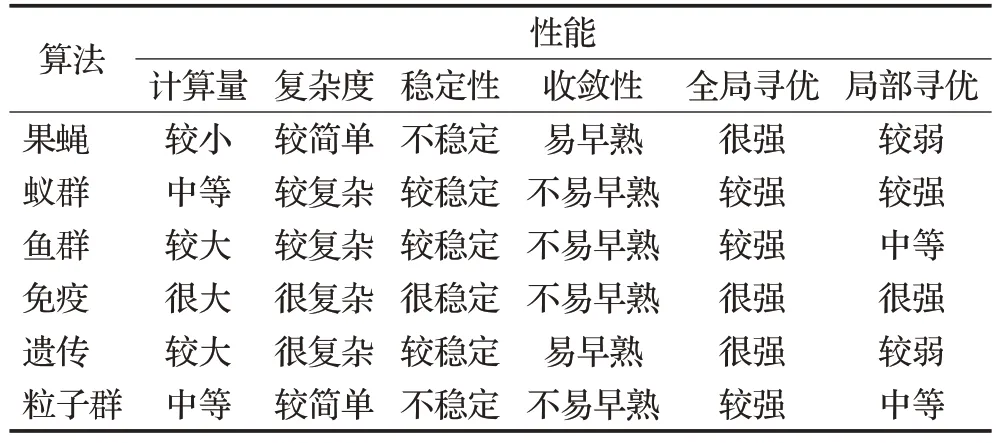
表1 FOA与其他群智能算法寻优性能对比结果

（1）初始化果蝇种群规模(Sizepop)和最大迭代次数(Maxgen)，初始化果蝇群体位置X_axis、Y_axis。

（2）每一只果蝇个体利用嗅觉搜索食物时，赋予其随机的搜索方向和距离：

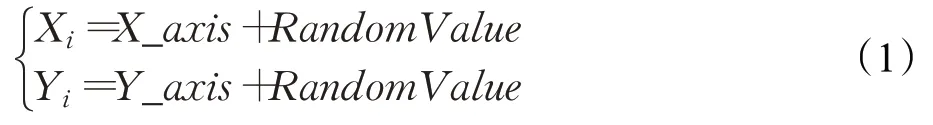
（3）由于一开始不知道食物的位置，因此先计算果蝇个体到原点的间距Disti，再计算味道浓度判定值Si：

（4）把味道浓度判定值Si代入到味道浓度判定函数（适应度函数或目标函数），计算出味道浓度值Smelli：

（5）找出果蝇种群中味道浓度值最优的那个果蝇，并记录此果蝇的位置信息和相应的味道浓度值：

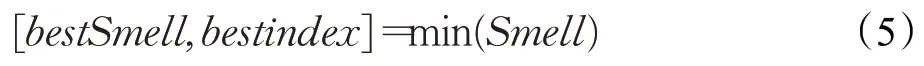
（6）保留最优的味道浓度值bestSmell，并利用视觉飞往步骤（5）记录的最优位置，进行位置更新，形成新的果蝇种群中心：

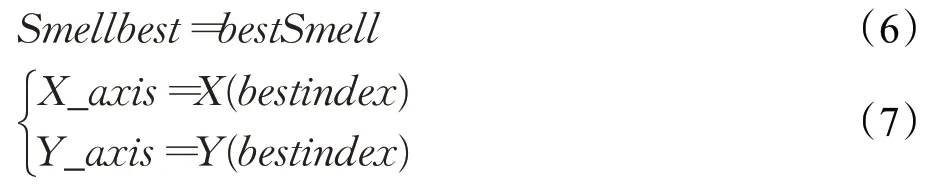
（7）开始迭代寻优，重复执行步骤（2）～（5），之后判断最优味道浓度值是否优于历史最优味道浓度值，若是且当前迭代次数小于Maxgen，则执行步骤（6）。

2 FOA的改进研究进展

从表1 中可以看出，FOA 虽然计算量较小，复杂度较简单，全局寻优性能良好，但是此算法容易过早收敛，稳定性不强，易陷入局部最优。针对FOA的不足，近年来众多学者做了大量的改进研究，改进思路主要从种群初始位置、候选解产生机制、搜索步长、多种群协同搜索、飞行策略以及设计混合算法等方面入手。

2.1 种群初始位置的改进

果蝇种群初始值的选择直接影响了算法本身的收敛速度和精度。当种群初始位置选取的当时，算法的收敛速度快且寻优精度高；反之算法的收敛速度慢，寻优精度低，且易陷入局部最优。因此，种群初始位置的改进是十分有必要的。目前已有的改进分析如下。

韩俊英等[9]提出了一种反向学习策略的果蝇优化算法，此算法是以一定的概率利用反向学习的策略来搜索反向解，之后从正向解和反向解中选择最好的作为种群初始值。王行甫等[10]利用佳点集产生的点无重复点且均匀分布等特性，提出了用佳点集方法在规定的区域内产生点，再从中选取最优的点作为果蝇群体初始位置。张水平等[11]通过等价替换来增大初始位置数量，之后根据混沌变量的遍历性和规律性，利用混沌映射确定种群初始位置。

2.2 候选解产生机制的改进

由于味道浓度判定值(Si)为距离的倒数，因此FOA不能找到带有负值的最优解，且Si不遵循均匀分布，易收敛于坐标原点，FOA找到非零最优解的概率极低，非常容易陷入坐标原点附近的局部最优。因此，算法的适用范围受到了极大的限制。针对以上缺陷，目前已有的改进策略如下：

（1）张勇等[12]提出加入有效因子α和避免局部最优因子β对果蝇优化算法进行改进，具体表达式如下：

（2）王念等[13]针对FOA 不能找到带有负值的最优解，提出了如下候选解产生机制：

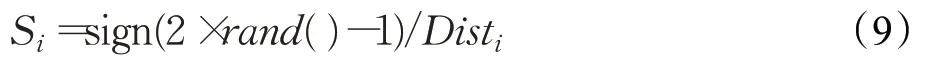
其中，rand()为[0，1]之间的随机数，当sign的数为负值时，则可得到负的候选解，但这种改进策略并没有解决候选解不均匀分布的性质，仍然易陷入坐标原点附近的局部最优。

（3）信成涛等[14]同样针对FOA不能找到带有负值的最优解，提出了如下候选解产生机制：

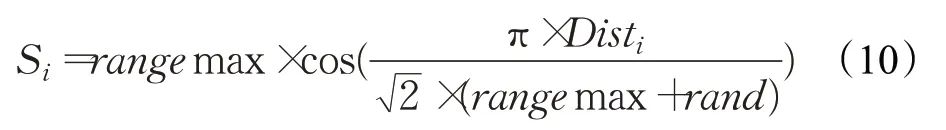
其中，rangemax 是单个果蝇搜索范围，rand为[0，1]的随机数。此改进方法利用余弦函数的对称性和周期性，使得候选解Si可以取负值，取值范围扩展为[-rangemax,rangemax]，且因为余弦函数的周期性，在一定程度上减小了算法陷入坐标原点附近的局部最优的概率，但是仍没有解决候选解分布不均匀的问题，不能在指定范围内均匀搜索。

（4）Cheng等[15]提出直接把Xi作为味道浓度判定值Si,Xi在全局搜索范围内随机初始化，这种生成机制真正的候选解为Xi，使得改进后的果蝇优化算法在整个有效搜索范围内遵循均匀分布，提高了算法的寻优精度以及求解非线性优化问题的能力。改进的果蝇优化算法Smelli的表达式为：

2.3 搜索步长的改进

搜索步长是群智能算法的关键参数之一，在标准果蝇优化算法中搜索步长为固定值，若搜索步长过大，果蝇的局部搜索能力变弱，反之，容易陷入局部最优使算法精度降低。改进的策略一般是将搜索步长的固定值改为动态的自适应值。相关改进策略如下：

（1）常鹏等[16]引入了速度进化因子Sd和果蝇群体聚集度因子Jd，使算法根据实际情况动态调整搜索步长R和搜索距离Dist的大小，来提高算法的寻优性能。相关公式如下（优化目标为最小值时）：

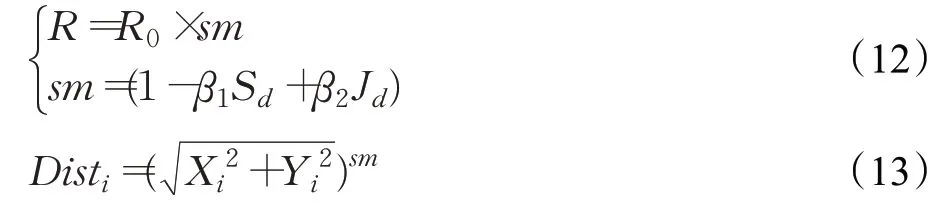
其中，R0为搜索初始值，sm为自适应调整因子，Sd为当前全局最优味道浓度值与上一次迭代的最优味道浓度值的比值，Jd为当前全局最优味道浓度值与当前迭代的前N次味道浓度平均值的比值，β1为Sd的权重系数，β2为Jd的权重系数。此改进方法虽在一定程度上提高了算法的收敛精度，但根据上述公式可推出sm的取值范围为[1-β1,1+β2]，因此其跳出局部最优的能力并不强，实验结果也表明在测试Rosenbrock函数时算法陷入了局部极小值。

（2）牛勇力等[17]通过自适应修改个体认知因子c1和群体引导因子c2的大小来调整搜索步长值。改进策略如下：

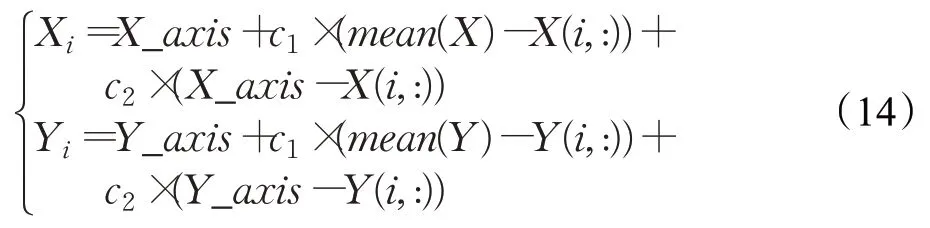
其中，c1=exp(min(Smell))-1 ，c2=1-c1，mean(X) 和mean(Y)是所有果蝇个体在此次迭代过程中位置的平均值。此改进策略避免了算法早熟，能跳出局部最优，提高了全局搜索能力，且具有更高的收敛精度和更快的收敛速度。但没有对候选解产生机制进行改进，无法求解最优解含负值的优化问题，极大地限制了算法的适用范围。

（3）王咏梅等[18]提出了一种新的动态搜索步长计算公式，此搜索步长计算公式充分考虑了全局与局部寻优能力的平衡，在算法迭代初期，搜索步长较大，使得算法在初期有较好的全局搜索能力，随着迭代次数的增加，搜索步长逐渐减小，以提升算法的局部搜索能力，并且当算法的全局最优解不再更新时，搜索步长会增大以跳出局部最优，有较好的跳出局部极值的能力。具体计算公式如下：

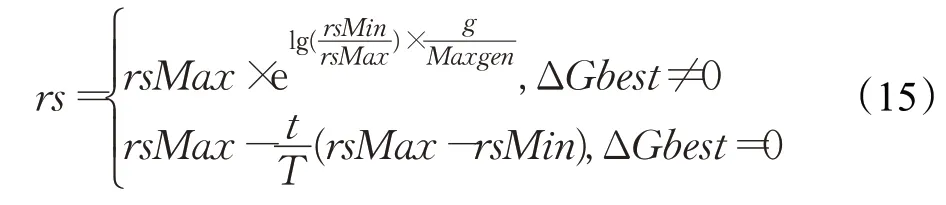
其中，g为当前迭代次数，rsMax、rsMin分别为最大搜索步长和最小搜索步长，ΔGbest是当前全局最优味道浓度值与上一次迭代所得的最优味道浓度值的差值，t表示当前反向搜索的次数，T表示需要反向搜索的总次数。此改进方法在提高算法寻优精度的同时，牺牲了较大的时间和空间复杂度，可以考虑结合多种群策略，减少反向搜索的次数，以降低时间复杂度。

（5）Cheng等[15]通过对高斯正态分布进行变换，设计了一种自适应调整的搜索步长，整个迭代过程搜索步长逐渐减小，且较好地平衡了全局寻优能力和局部寻优能力。在迭代初期，搜索步长减小得极慢，随着迭代次数的增加，开始缓慢地减小搜索步长，保证算法在迭代初期能够在全局搜索领域内进行充分的搜索，提高全局搜索能力，降低陷入局部最优的概率；之后，再快速减小搜索步长，到迭代中后期之后，又开始缓慢减小搜索步长，以保证算法在后期局部寻优的能力，大大提高了算法的寻优精度。具体数学表达式如下：

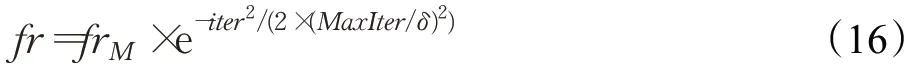
其中，frM决定了高斯分布的高度，δ的取值范围为[5，10]。同时，引入了少量精英果蝇，精英果蝇搜索步长不随迭代递减，提高了算法后期跳出局部最优的能力。此改进策略虽然提高了算法的寻优精度，但算法前期为了充分搜索全局，搜索步长减小得极慢，因此在实验中算法前期收敛速度相比于其他对比算法要更慢。

2.4 多种群协同搜索

FOA在搜索过程中易陷入局部最优，因丧失种群多样性而早熟收敛[19]。多种群协同搜索通过设计合理的种群数量维持种群多样性以及设计合理的种群间信息交换策略来提高搜索精度和搜索效率。目前已有的改进策略分析如下：

（1）张前图等[20]提出当果蝇个体离当代种群最差个体更近时，将其划分到以当代最差个体为中心的较差子群，当果蝇个体离当代种群最优个体更近时，则划分到以当代最优个体为中心的较优子群，依照此规则将果蝇种群动态地一分为二，两个子群执行不同的搜索策略，同时通过最优个体的改变和子群的重组进行两个子群间的信息交换。此算法改进策略提高了种群多样性，平衡了算法的全局和局部的搜索能力，能更好地跳出局部最优。但是改进后的算法并没有解决只能求解非负最优解的问题。

（2）胡丽芳等[21]提出子群A和子群B交替搜索的双子群果蝇优化算法。两个子群的群体位置由当前迭代结果与上一次迭代结果相比较来交替取值。在标准果蝇优化算法中，所有果蝇个体都向最优果蝇个体聚集，削弱了算法后期的种群多样性，加大了算法陷入局部最优的风险，此策略的优点是增加了种群多样性，且当子群A搜索步长过小导致算法早熟时，子群B的搜索步长则会比较大，此时，可用子群B取代子群A，改变算法的搜索空间，避免陷入局部最优。子群A与子群B的搜索步长公式如下：

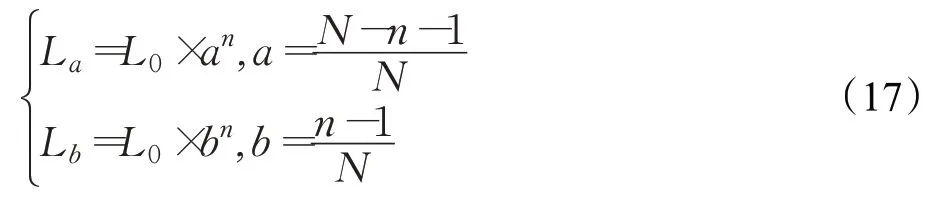
其中L0为搜索步长初始值，n为当前的迭代次数，N为最大迭代次数。

李栋等[22]和Wu 等[23]也均提出了双种群策略，两个种群分别强调局部搜索和全局搜索，后者在双子群策略基础上同时结合了云模型理论，提出了一种基于云模型的双种群FOA。

（3）张强等[24]用自适应分组策略来模拟自然界中生物的领域特性，并且在进化过程中设置一个果蝇精英池。将果蝇种群分成m个规模相同的子群，把果蝇种群内的个体按味道浓度值降序排列，将前m个果蝇依次分配给m个子群，则第m+1 个果蝇进入第1个子群，依次类推，并采用贪心策略用当代最优果蝇个体更新果蝇精英池的个体，将果蝇精英池中的个体进行差分变异操作去改进最优果蝇个体的搜索方式。计算精英果蝇池内果蝇个体的方差，以此来衡量果蝇精英池内果蝇个体的离散程度，作为分析个体多样性的标准。方差越低，果蝇个体分布越密集，味道浓度值变化缓慢，个体多样性降低。在迭代后期，当味道浓度值变化缓慢，精度不变化次数达到设定上限值时，将整个种群分为拓展群体和优势群体，分别用反向混沌算法和改进粒子群算法优化拓展群体和优势群体，避免陷入局部最优和提高寻优精度。郑晓龙等[25]也采用了多种群机制，并利用个体间的差分信息作为协同搜索机制，提高了种群多样性和搜索效率。

2.5 飞行策略的改进

由于FOA 算法的全局搜索能力不足，算法易早熟陷入局部最优，因此改进果蝇的飞行策略，尤其是果蝇的飞行方向与距离是非常有必要的。近年来已有的研究分析如下：

Wang 等[26]提出了一种概率飞行策略，果蝇每次搜索时都会以一定概率选定飞行范围，且范围越大概率越小，此飞行策略的改进提高了算法的搜索精度。王行甫等[10]以一定概率执行柯西变异对果蝇群体中最优个体进行扰动，对变异后的种群进行二次寻优，提高了算法跳出局部极值的能力和寻优效率。张水平等[27]提出加入精英个体，在算法初期以线性递减的牵引因子来诱导精英个体协同寻优，在算法后期采用搜索空间压缩的搜索策略，此改进方法能提高算法跳出局部最优的能力。盛超等[28]在FOA中加入跳跃机制，当浓度方差值连续低于设定阈值且低于设定阈值总次数到达设定上限时，利用t分布的随机性和散布特性更新果蝇位置使算法跳出局部最优。Fan等[29]引入了一种有效的鲸鱼狩猎策略来代替原始FOA 的随机搜索计划，并通过21 种测试函数进行性能测试，以验证其有效性，统计数据表明，已改进的算法有效地扩大了原始FOA的勘探和开发能力。Li等[30]采用种群中最好的果蝇诱导最差果蝇飞行的策略，当连续几次迭代果蝇状态仍未更新，则会被随机生成的果蝇所取代，这种策略可以帮助算法跳出局部最优。石建平等[31]提出双策略协同进化的搜索方法，策略一是使当前果蝇向精英个体学习的同时，引入种群中不同果蝇个体之间的差异信息，以确保搜索结果的多样性，提高全局搜索能力，避免算法只向最优个体学习，丧失种群多样性，陷入局部最优。策略二是对历史最优个体利用自身记忆信息去构建差分向量，该策略能有效加快算法的收敛速度。两个策略交替使用，在迭代前期以较大概率使用策略二进行搜索，加快前期的收敛速度；在迭代后期则以较大概率使用策略一进行搜索，避免向最优个体聚集而陷入局部最优，有较好的跳出局部极值的能力，合理地平衡了算法的全局搜索与局部搜索的能力。

2.6 设计混合算法

果蝇优化算法具有简单易实现的搜索框架，故很容易与其他方法相结合，构造出能较好地平衡局部搜索能力与全局搜索能力的混合算法。

潘欣等[32]将FOA与差分进化算法相结合，对每次迭代产生的果蝇群体进行若干次变异、交叉、选择等差分演化操作，增加种群多样性，提高算法的执行效率和收敛速度。使用了12个基准函数对改进后的算法进行性能测试，结果表明新算法在收敛速度和精度上明显优于FOA。王龙飞等[33]将FOA与遗传算法相结合，运用交叉运算的思想，把前一次迭代产生的果蝇群体一分为二两两交叉组合，得到新的子代群体，重新计算最优味道浓度值，判断是否优于交叉前最优个体味道浓度值，选出二者之间更优的最优果蝇个体位置作为下一次迭代的种群初始位置，此方法在迭代过程中增加了种群多样性，提高了算法跳出局部最优的能力，但是较大程度上增加了算法的复杂度，运行效率并不高。贺智明等[34]提出一种基于元胞自动机的果蝇优化算法（CAFOA），以FOA 为主框架，在寻优过程中引入元胞自动机演化规则。对6种经典测试函数进行性能测试，仿真实验结果表明CAFOA相比FOA平均收敛精度提高10%，且具有较好的稳定性。Szczypta 等[35]将FOA 与混合遗传算法相结合，并应用到参数优化控制和结构选择之中。刘成忠等[36]将FOA与混合蛙跳算法相结合，提出了局部深度搜索的混合果蝇优化算法（SFOALDS）。实验结果表明，SFOALDS有较强的全局搜索能力，且在求解高维函数时优势更加明显。

3 FOA的应用研究

自果蝇优化算法提出以来便受到了众多学者的广泛关注与研究。目前，FOA已在多个领域得到广泛应用。

3.1 复杂函数优化

检验算法性能的重要标准之一是对复杂函数的寻优能力，因此，有众多学者致力于求解复杂函数优化问题。张晓茹等[37]提出一种微果蝇优化算法用于求解多模态函数优化问题，实验结果表明在偏高维多模态函数优化问题上具有较好的应用潜力。Wu等[38]用基于云模型的FOA测试了包括单峰和多峰的多个复杂复合函数，实验结果表明其性能要优于其他群智能算法。Wang等[39]将FOA 应用于求解离散的多维背包问题。张健等[40]采用分群策略和动态半径来改进果蝇优化算法，并应用在多目标搜索领域解决了多目标背包问题。臧文龙等[41]引入避免局部最优因子来改进FOA 的多目标问题。Niu 等[42]提出基于差分操作的FOA，并用于求解最优解不在零点的高维复杂函数。朱志同等[43]将改进的果蝇优化算法用于求解混合整数非线性规划问题，实验结果表明，在算法稳定性、收敛速度等方面，改进的果蝇算法相比于粒子群算法及差分进化算法要更优。FOA 在复杂函数优化方面的应用较多，尤其是在高维、多峰函数优化方面的应用，但在多约束条件函数优化、离散函数优化等方面的应用研究相对来说还比较少。

3.2 参数优化、预测

宁剑平等[44]利用递减步长的果蝇优化算法（DS-FOA）优化支持向量机模型的惩罚因子参数和核函数参数，仿真实验结果表明，DS-FOA 与 FOA、PSO 和 GA 算法相比，优化参数的支持向量机回归模型回归效果好，均方误差最低。针对大多数支持向量机仅考虑边距，而忽略半径，Gu等[45]利用FOA建立了一种基于半径-边距的支持向量机模型，该模型考虑了边距的最大化和半径信息最小化。利用FOA 对惩罚因子参数优化。针对8 个UCI 数据集和8 个比较算法，评估了所提出的方法的有效性。实验结果验证了其可以产生更合适的模型参数并降低计算成本，从而产生较高的分类精度。南敬昌等[46]将改进的FOA 用于优化广义回归神经网络的光滑因子，并应用于预测电压驻波比参数和天线的S11 参数。Zhou 等[47]在FOA 中引入了模糊密度机制，以增强果蝇个体的搜索能力，将改进后的果蝇优化算法用于优化半监督亲和力传播模型的参数。并利用改进的模型来分析地震数据，聚类结果表明，该模型具有较好的应用价值。程宏伟等[48]为提高预测接地网腐蚀速率的精度，利用改进后的果蝇优化算法优化BP神经网络的阈值和初始权值，并通过实验验证了其有效性与可靠性。陈明扬等[49]利用改进的FOA 优化回声状态网络参数并用于预测旅游需求。郭晓芸等[50]利用定向变步长的果蝇优化算法优化概率神经网络（PNN）参数，用于诊断变压器故障。李明辉等[51]将改进的果蝇优化算法用于PID 参数优化。张亭亭等[52]同样对PID参数进行优化，并应用于电地热温度控制系统。随着“中国制造2025”计划的出台，制造业的未来已经从“中国制造”转变为“中国智能制造”，这意味着智能技术的新时代已经来临，Wang等[53]运用果蝇优化算法对多元回归进行优化，构建模型，有效地预测中国智能技术产业的企业经营绩效，实验结果表明，果蝇优化算法具有较好的多元回归优化能力，明显提高了预测性能。为了增强Z-Score 财务预警模型预警能力，康彩红等[54]用改进的FOA 来优化Z-Score模型的参数，测试结果验证了此算法，有效地提高了Z-Score财务预警模型预测能力。FOA在参数优化方面的应用主要是对支持向量机参数、神经网络参数、PID控制器参数等其他参数进行优化，用于预测电力负荷、旅游需求、企业经营绩效等不同领域的各种指标，且都达到了一定的预测效果。

3.3 调度、物流问题

Fu等[55]结合随机模拟方法，提出了一种多目标离散果蝇优化算法，并应用于多目标集成拆卸-再加工-再装配调度问题，需要同时考虑多目标和不确定性，达到最大完工时间和总延误最小化的目标。为了解决分布式置换流水线调度问题，王凌等[56]提出了混合离散果蝇优化算法，并通过仿真实验验证了此算法的有效性。黄元元等[57]将混合果蝇优化算法应用于分布式异构并行机调度问题，实验结果表明此算法具有较好的稳定性。苏楷等[58]提出了一种改进的FOA，用于求解以运输成本最小为目标的露天矿运输调度问题。吴斌等[59]利用矩阵编码方法重构FOA 并用于解决员工现场服务调度问题。秦书婷等[60]针对物流配送路线规划问题，考虑配送路程以及配送点之间能否直接通行等因素，引入基因互换和邻域探测搜索对FOA 进行改进。实验结果表明，改进后的算法所得到的配送路线方案非常合理。总之，FOA在解决流水线调度、运输调度、一般物流配送等问题的应用都取得了不错的效果，但对动态不确定需求下的库存、配送等问题的应用研究还相对较少。

3.4 图像及其他应用

刘亚如等[61]提出将FOA与支持向量机相结合，并应用于火灾图像识别，实验结果表明此方法对火灾图像识别准确率有所提高，对火灾检测具有实际应用价值。李美丽[62]以平均结构相似度作为目标函数，利用改进的FOA优化脉冲耦合神经网络参数，对源图像进行融合。对医学图像的融合以及可见光与毫米波图像的融合进行仿真实验，实验结果显示图像融合效果优于常用方法。为了解决图像分割效率不足问题，宋杰等[63]提出自适应变步长的FOA，优化大津法图像分割阈值。实验结果表明此改进虽在优化阈值方面效果比其他算法好，但当阈值数较大时，其稳定性有所下降。今后，可在提高算法稳定性上继续深入研究。Zhang 等[64]利用FOA 对最小二乘支持向量回归的两个参数进行优化，训练最小二乘支持向量回归来学习退化图像和原始图像之间的映射关系。通过所获取的映射，可以恢复退化的图像。实验结果表明，该方法能获得满意的修复效果。与BP神经网络回归、SVR方法和Lucy-Richardson算法相比，其恢复速度更快，并具有更好的性能。近年来，FOA在图像上的应用主要还是结合其他算法及方法对图像进行图像识别、图像融合、图像分割等操作。除此之外，FOA 的应用还涉及了很多其他领域。段艳明等[65]利用改进的FOA 求解旅行商问题，其改进的算法在算例规模较小时能快速收敛到已知最优解，在算例规模较大时也能接近理论最优解。为了增强在结构中粘滞阻尼器的抗震减震效果，伍宏科等[66]利用基于云端模型的FOA优化建筑粘滞阻尼器布置方案，并通过实验证明了该方案的可行性，提高了抗震减震的效果。更多FOA 相关应用研究可见文献[67-69]。

4 结语与展望

本文归纳总结了果蝇优化算法的相关改进与应用，对搜索步长、飞行策略等关键改进方法进行了详细说明，对参数优化、调度、物流等相关应用进行了分类汇总，归纳梳理了近几年的研究进展。虽然FOA 具有结构简单、易于构建的代码框架、可操作性强等优点，但目前依旧处在探索阶段，发展还不够成熟。未来对FOA 的理论研究、算法改进及实际应用还有很大的发展空间。

（1）理论研究：目前，对FOA 的理论研究非常少。FOA的视觉搜索和嗅觉搜索是决定FOA性能的核心要素，将其对FOA 的影响作出理论性的分析是非常值得研究的一个方向，可以对算法的改进作出理论性的指导。对算法的全局优化与局部优化能力的平衡也需要更加深入的理论分析。除此之外，还可以从理论上去分析影响收敛速度的因素以及参数的敏感性等，为FOA实际应用提供有力的理论支撑。

（2）算法改进：可以根据FOA的算法流程做出相应改进。种群初始位置是影响算法收敛速度和精度的直接因素，目前针对种群初始位置改进的方法并不多，是值得关注的方向。让候选解能均匀地分布于解空间，用于解决非零最优解的复杂函数，增加算法的适用范围也是今后值得关注的研究方向。提升FOA全局搜索能力的重要手段之一是增加种群多样性，如何设计合理的种群数量以及种群间高效的信息交换策略，是可深入研究的方向。果蝇种群的进化方向是有一定规律性的，可考虑研究进化方向的规律，设计合理的坐标变换公式，如计算前两次进化方向间的夹角，以一定权重指导群体中一部分果蝇做具有方向性的搜索，以加快寻优速度。还可考虑借鉴其他生物群体趋利避害、竞争、分工等行为，引入新的搜索策略。设计混合算法是算法改进的重要途径，目前已有一些将FOA 与其他算法相结合的改进研究，未来可继续研究将FOA 有所不足的地方（易早熟、稳定性不强等）与其他算法在这些不足之处却有优势的算法相结合，优势互补，提高算法的适用性、高效性。

（3）实际应用：FOA已在多个领域得到应用，但大部分研究还是将FOA 用于参数优化和组合优化方面，而在更具现实意义的离散优化、多目标优化、约束优化以及动态不确定性等领域应用较少。可以分析现有的优先关系法、随机权重、目标简化等方法的优缺点，将寻优策略与有效的多目标处理方法相融合，利用熵分析、主分量分析等手段对多目标问题进行降维处理。也可以考虑参考模糊集、随机图、约束满足等理论和方法，提出较为高效地用于解决不确定性问题的果蝇优化算法。还可以考虑与分支定界法、割平面法等精确算法相结合，利用FOA快速得出解的取值范围，之后再用精确算法求出最优解。未来的研究工作可在离散组合优化、多个调度目标的协同优化、其他不确定问题的扩展、自适应算法的设计以及其他调度指标的优化等方面不断拓展。