基于CEEMD-PSO-MNN 的船舶航迹预测*

王文标，董贵平，汪思源，孟 松，杜大鹏，杜佳璐

(大连海事大学船舶电气工程学院，辽宁 大连116026)

随着我国海洋事业的发展以及船舶使用数量和频率的增大，海上交通事故呈现出不断上升的趋势，海上交通的安全状况不容乐观。 为提高海上交通安全，实时准确地预测船舶未来时刻的航迹信息对于海上交通研究与管理、船舶智能避碰有重要意义。

对于船舶航行行为预测，现阶段常用的方法有支持向量机[1]、卡尔曼滤波[2]、灰色预测模型[3]等。其中，支持向量机虽然有着不错的精度但对于大数据量问题的解决尚有不足。 灰色预测模型虽然计算简便，但在序列波动剧烈的情况下无法满足高精度要求。 随着神经网络研究的不断深入，基于神经网络的船舶航行行为预测方法得到了大跨步发展[4-10]。 然而，上述神经网络方法均为单一全互连神经网络预测模型，当面对多纬度、大数据量等特点的预测任务时，其无法准确地体现出预测序列的非线性，导致模型预测精度受到影响。

针对上述问题，本文提出一种基于CEEMD、FE、PSO 与MNN 的船舶航迹预测方法。 首先使用CEEMD 将船舶航迹时间序列分解为不同的本征模态函数及趋势项；然后通过FE 将各本征模态与趋势项划分到不同的子网络中进行学习，实现MNN分而治之的设计理念；最后利用PSO 优化MNN 子网络学习参数达到船舶航迹的精准预测。 通过对比实验验证了本方法的准确性和实用性

1 互补集合经验模态分解

经验模态分解(EMD)是一种适合于分析和处理非线性和非平稳信号的方法[12]。 该方法将任意信号过滤到不同尺度的确定性IMF 和残差分量中。其核心是对信号进行逐层筛选，对不同频率的信号进行不同层次的分解。

每个尺度的IMF 必须满足以下两个要求:

(a)在整个数据序列中，极值点和过零点的数量必须相等或最多相差一个。

(b)数据序列在任意时刻的局部均值为零。

然而EMD 相对容易引起模态混合，为了避免这个问题，引入互补集合经验模态分解(CEEMD)对时间序列进行分析[13]。 CEEMD 是EMD 的一种改进算法，利用噪声特性可以有效地减少模态混合现象的发生，CEEMD 分解基于EMD，其实现过程如下步骤:

(1)在原序列中加入N 对白噪声，得到一个包含2N 个信号的集合。 辅助噪声为高斯白噪声，ni(t)，i＝1，2，…，n。

式中:IMFj为通过CEEMD 对原始信号进行分解得到的IMF。

2 模块化神经网络结构设计

模块化神经网络(MNN)旨在通过执行“分而治之”来解决复杂的问题[14-15]。 如图1 所示主要由三个功能层组成:任务分解层，子网络层和输出层，本文主要在子网络层进行了部分改进。

图1 模块化神经网络系统结构

2.1 任务分配

将一个难以学习的任务分配成多个容易学习的子任务是实现“分而治之”的前提，文中采用模糊熵辅助任务分解。

2.1.1 模糊熵

模糊熵(FE)是信息论和模糊逻辑的跨学科概念。 模糊熵的概念最初是由近似熵(AE)和样本熵(SE)的研究启发而来，用于量化复杂系统科学和混沌理论中非线性时间序列的不规则性[16]。 与AE和SE 相比，FE 在描述不同不规则性的信号时，具有更好的单调性和相对一致性，并且对噪声具有更强的鲁棒性，模糊熵求解如下:

(1)设原始时间序列为x(j)，j＝1，2，…，M。

(2)重构一组n 维矢量定义如下:

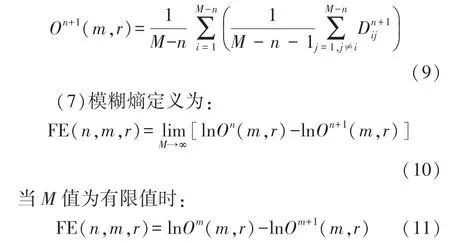
式中:共涉及3 个参数的选择，通常情况下较大的m能更细致地重构系统的动态演化过程，一般取m ＝2。边界梯度n 的增加，会在一定程度上影响模糊熵的细节信息，一般取n＝2；r 的取值也是一个值得考虑的问题，过大的相似容限会导致信息丢失，相似容限值越大，丢失的信息越多，而太小的相似容限度则会增加结果对噪声的敏感性，一般定义r 为0.2*SD，其中SD 为原一维时间序列的标准差。

2.2 PSO-LSTM 子网络设计

子网络的性能决定了整个神经网络性能，子网络对子任务的学习就相当于整个神经网络对任务进行训练的过程，本文选用粒子群算法改进LSTM 神经网络作为模块化神经网络的子网络对船舶航迹进行预测。

2.2.1 粒子群优化算法

粒子群优化算法(PSO)于1995 年提出，用于研究鸟类的捕食行为，并被扩展到解决优化问题[17]。在使用PSO 算法寻优时，将每个问题的解看作空间中没有质量和体积的粒子，将每个粒子的位置看作空间的解。 飞行速度可根据个体和群体飞行经验的分析结果随时调整。 在d 维空间的每次迭代中，粒子通过寻找两个解来优化其位置和速度，这两个解分别是个体极值Pbest和全局极值Gbest。 粒子i 第k次迭代的速度和位置更新公式可以表示为:

2.2.2 长短期记忆神经网络

长短期记忆神经网络是循环神经网络的改进版本，其具有良好的非线性映射能力，能够跟踪系统的动态特性，在处理时间序列问题时的表现非常优秀[18]。 基于LSTM 神经网络这种出众的能力，本文用其学习输入部分的动态变量。 与循环神经网络不同的是LSTM 神经网络核心设计包括三个门，即输入门、遗忘门和输出门如图2 所示。

图2 LSTM 神经网络结构

式中:i、f、～c、o—输入门、遗忘门、LSTM 网络细胞和输出门在t 时刻的计算公式；x、h 为t 时刻的输入与输出；c 为细胞更新公式；σ 与tanh 分别为Sigmoid激活函数与双曲正切函数。

通过LSTM 神经网络的门控机制能有效地避免传统循环神经网络随着时间间隔的增加容易出现梯度爆炸后梯度消失等问题。

2.3 输出层

输出层仅在网络测试时有效，本文输出层选择竞争方式。 也就是说，只有性能优越的子网络才有助于最终输出。 输出层公式:

式中:Y、YCL、YL、EL、ECL分别为模块化神经网络最终输出、CEEMD 分解后子网络输出、未CEEMD 分解子网络输出、未CEEMD 分解子网络测试误差绝对值之和、CEEMD 分解后子网络测试误差绝对值之和。

3 实验结果及分析

文中通过均方误差(MSE)与平均绝对误差(MAE)对网络整体性能进行评估，其值越小，代表预测精度越高。 其公式如下:

式中:Y 为网络的预测值，y 为网络实测值，i ＝1，2，…，P，P 为训练样本个数。

3.1 预测模型对比实验

文中采用秦皇岛至大连段本校训练船真实船舶AIS 航行数据集，选择船舶航速在0～13kn(节)段内的船舶航迹数据，数据间隔为10 s。 按照时间排序将其前9/10 用于训练后1/10 用于测试，船舶航迹预测流程如图3 所示。

图3 船舶航迹预测流程图

首先将船舶航迹时间序列进行CEEMD 分解，分解后的本征模态分量IMF 与剩余分量Re 分别计算模糊熵以此判断时间序列的复杂性；然后将模糊熵求均值以得出判断时间序列复杂度的阈值；最后通过阈值将IMF 与Re 进行任务分解。 在此基础上，未进行CEEMD 分解的船舶航迹时间序列同样进入子网络学习。

3.2 CEEMD 分解

以船舶纬度时间序列为例，将时间序列按照CEEMD 分解获得具有不同波动尺度信息的本征模态分量，其中得到7 个基本模式分量IMF 1 ～IMF 7和一个剩余分量Re。 IMF 1 与IMF 2 的频率较高，代表船舶纬度信号中的高频成分；而Re 是低频信号，代表信号中含有的非线性趋势项。 图4 为船舶纬度时序曲线及进行分解后的各模式分量。

图4 船舶纬度时间序列CEEMD 分解结果

将船舶航迹纬度CEEMD 分解后的IMF 与Re进行模糊熵计算以此来量化序列的复杂程度，将模糊熵值小于模糊熵阈值的分量传输到同一子网络进行学习，模糊熵值大于模糊熵阈值的分量传输到各自单独的子网络进行学习，各分量模糊熵值如图5。

图5 IMF 的FE 值

船舶航迹预测结果如图6，经度预测结果及误差如图7，纬度预测结果及误差如图8。

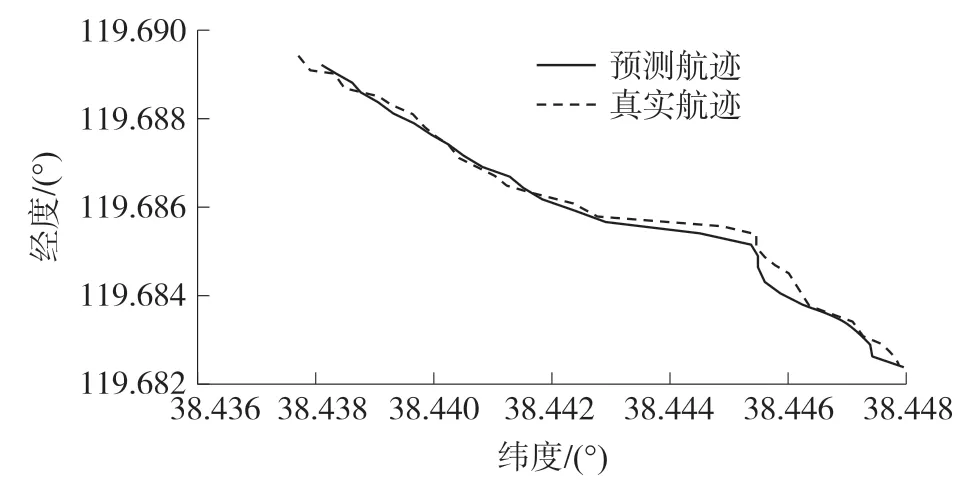
图6 航迹预测结果

图7 经度预测及误差

图8 纬度预测及误差

为进一步验证本文所提方法对于舶航迹预测的优越性，采用不同预测算法进行对比。

如表1 所示，本文所提方法整体性能高于其他预测模型，全互连神经网络预测模型性能明显低于模块化神经网络预测模型，验证了“分而治之”理念的有效性；使用PSO 进行优化的MNN 预测精度高于未使用PSO 优化的MNN；在PSO 优化MNN 情况下的纬度预测过程中，CEEMD 的作用优于EMD。综上所述可以推断出本文所提CEEMD-PSO-MNN船舶航迹预测方法比其他方法更好。

表1 不同预测模型评价指标

4 结束语

为进一步提高船舶航迹预测精度，提出一种CEEMD-PSO-MNN 的预测方法。 基于CEEMD-FE的任务分解(分而治之)方式有效地将复杂的航迹预测任务拆分为不同的子任务，降低了模型的复杂度；PSO 优化算法提高了MNN 子网络的预测精度。对比实验表明本方法整体性能优于全互连Elman 神经网络与全互连BP 神经网络。 验证了本算法的准确性与实用性。