融合伽马变换及分数阶的低照度图像增强算法
杨先凤,蒋欣岑,杜晶晶
(1.西南石油大学 计算机科学学院,四川 成都 610500;2.广安职业技术学院 智能制造与能源工程学院,四川 广安 638500)
0 引 言
由于受到多方面因素的影响,一些图像不够清晰或对比度较低,造成图像特征不能很好体现,给分析和识别带来困难[1-3]。因此,改善图像质量,提高信息的可认知性尤为重要。低照度图像常用的增强算法一般是基于直方图的增强方法、基于滤波器的方法及二阶微分拉普拉斯算子等[4,5]。但是这些方法对增强高频分量效果较好,对低频部分效果不明显甚至在增强过程中会丢失某些细节信息。
在图像增强中,分数阶微分在增强高频成分的同时又能实现对中低频成分的增强,在一定程度上又能非线性保留图像的直流成分,使图像纹理细节更加清晰,克服了整数阶微分会削弱低频信息的缺点[6,7]。但它不能有效提高图像的亮度、对比度。尤其当图像为低照度图像时,分数阶的优势未被充分显示出来。为了充分发挥分数阶的优势,本文引入伽马变换提出一种融合伽马变换及分数阶的低照度图像增强算法。该算法首先利用局部信息与直方图确定伽马参数,使用改进的伽马变换对低照度图像进行亮度与对比度的提高;接着利用分数阶微分增强对图像进行细节增强。在该步骤本文针对邻域像素对中心点的不同影响,设计了新的加权模板;根据对纹理及边缘实现不同程度的增强确定分数阶次函数表达形式,并依据邻域信息自适应确定分数阶次的具体取值。本文提出的方法充分利用了伽马变换与分数阶增强的优势,同时能达到图像的亮度、对比度及细节信息的增强,还能抑制过增强。
1 改进的伽马变换
由于伽马变换能改善图像质量,对图像光照进行有效校正,且计算简单而被广泛运用[8]。大多伽马变换的参数都是手动设置且为全局,增强效果并不理想。本文在文献[9]的基础上对伽马变换做了进一步改进,将算法中的参数都设置为自适应且考虑原图像的亮度信息,提高增强效果。
伽马变换定义如下
(1)
式中:f表示输入的待处理图像;fmax为图像f中的最大像素值;1-cf(i,j)整体为伽马参数,主要用于控制增强的程度;cf(i,j)表示与邻域信息与直方图相关的加权累计概率和,其计算步骤如下:
(1)计算输入图像f每一灰度级的概率密度pf(k)及对应的pfα(k)
(2)
pfα(k)=pf(k)α
(3)
式中:nk表示图像f中像素值为k的总像素数;MN为总的像素个数;α为大于0的调整因子。
(2)计算输入图像f每一像素点对应的加权累计概率和cf(i,j)
(4)
调整因子α的取值会影响最终图像的增强效果。当α越大时,增强效果越明显。在该伽马变换下取不同全局α值时的效果如图1所示。
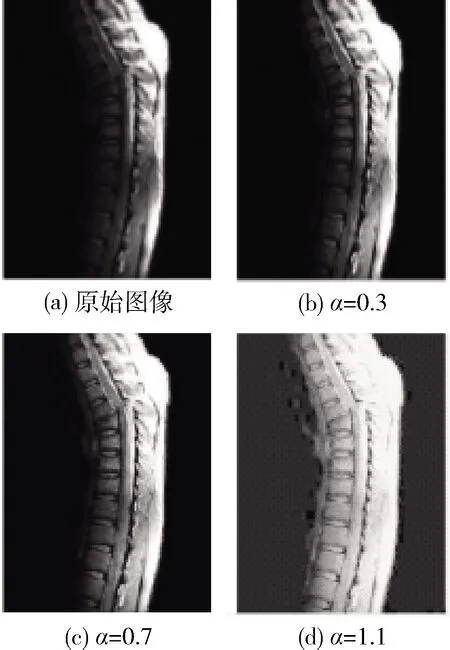
图1 不同α值下的实验结果
从图1可以得出增强效果随着α值的增强而增强,但是增强力度越大图像细节丢失越严重,手动设置全局α值并不能得到理想的增强图像。为了克服该缺陷,本文根据图像的邻域及原图的亮度信息自动确定α值。在图像背景区α取值可以稍大;细节信息丰富的区域α取值稍小,主要保护细节信息。在数字图像中信息熵、梯度和方差能较好描述图像的纹理细节信息。因此,采用这3个值及亮度来确定α的具体值。
图像信息熵反映了图像中平均信息量的多少。在图像邻域中局部信息熵和强度变化有关。图像局部信息熵越小,说明该区域为平滑区;纹理和边缘越丰富的区域,局部信息熵越大
S=∑i∈wPilogPi
(5)
式中:S为以某一像素点为中心且以w=m×m为窗口大小的局部信息熵;Pi为窗口中的灰度级出现的概率。
图像梯度是最能反应像素间差异大小的指标。因此,可以根据图像局部区域的平均梯度值判断该区域的纹理或边缘是否丰富。一幅二维数字图像f(i,j)的梯度幅值为
(6)
则以任一像素点为中心且窗口大小为w=m×m的局部区域的平均梯度为
(7)
在概率论和统计学中,方差用来衡量数据的离散程度。将其运用于图像中可以反映区域纹理的复杂程度。设图像f(i,j)的局部均值和局部方差分别为Ew,Dw,w=m×m为邻域窗口。则有
(8)
(9)
最终三者的局部信息加权和记为x
x=λ*S+β*H+γ*Dw
(10)
式中:λ,β,γ为加权系数,且λ+β+γ=1。图像中平均梯度比局部信息熵及方差更能体现图像特征,同时也参考文献[10]的设置方式及多次实验,本文取λ=0.3,β=0.5,γ=0.2。
本文除了利用局部细节信息外还引入了原图像的亮度来确定α,从而减小原始图像亮度对算法的影响
(11)
式中:fb为原始输入图像f的平均亮度,由于α>0,因此x在应用于式(11)前应当归一化。运用本文提出的式(11)确定α值的实验结果如图2所示。
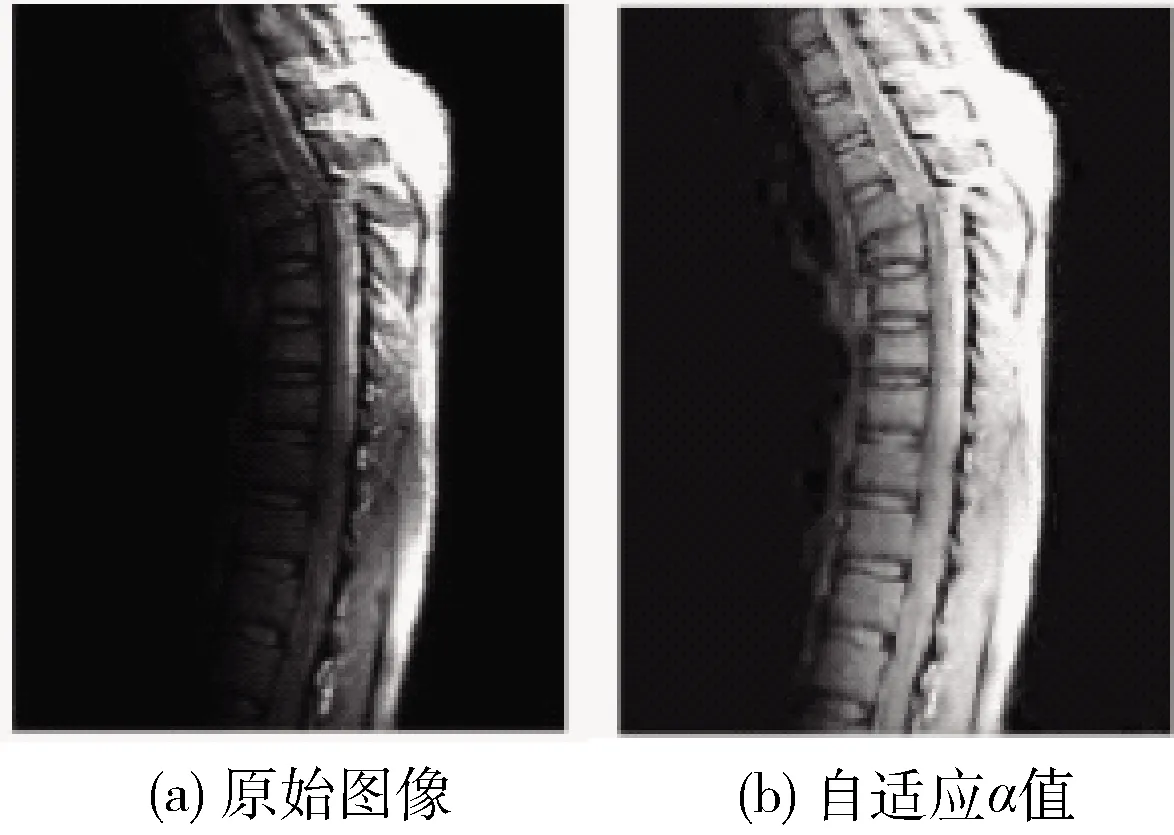
图2 自适应α值实验结果
通过图2与图1的实验结果对比可知,自适应的α值相比于全局的α值能产生更好的增强效果,细节更明显,图像的层次也更强。为了使图像的细节信息更明显,接下来本文使用分数阶对伽马变换后的图像进行细节增强。
2 改进的分数阶增强
2.1 分数阶微分的差分表达式
Caputo定义是最常用的3种分数阶微积分定义之一,是对G-L定义的一种改进。将分数阶微分应用于图像增强时,需要先将其定义转化为差分形式。Caputo定义[6]
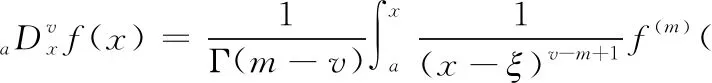
(12)
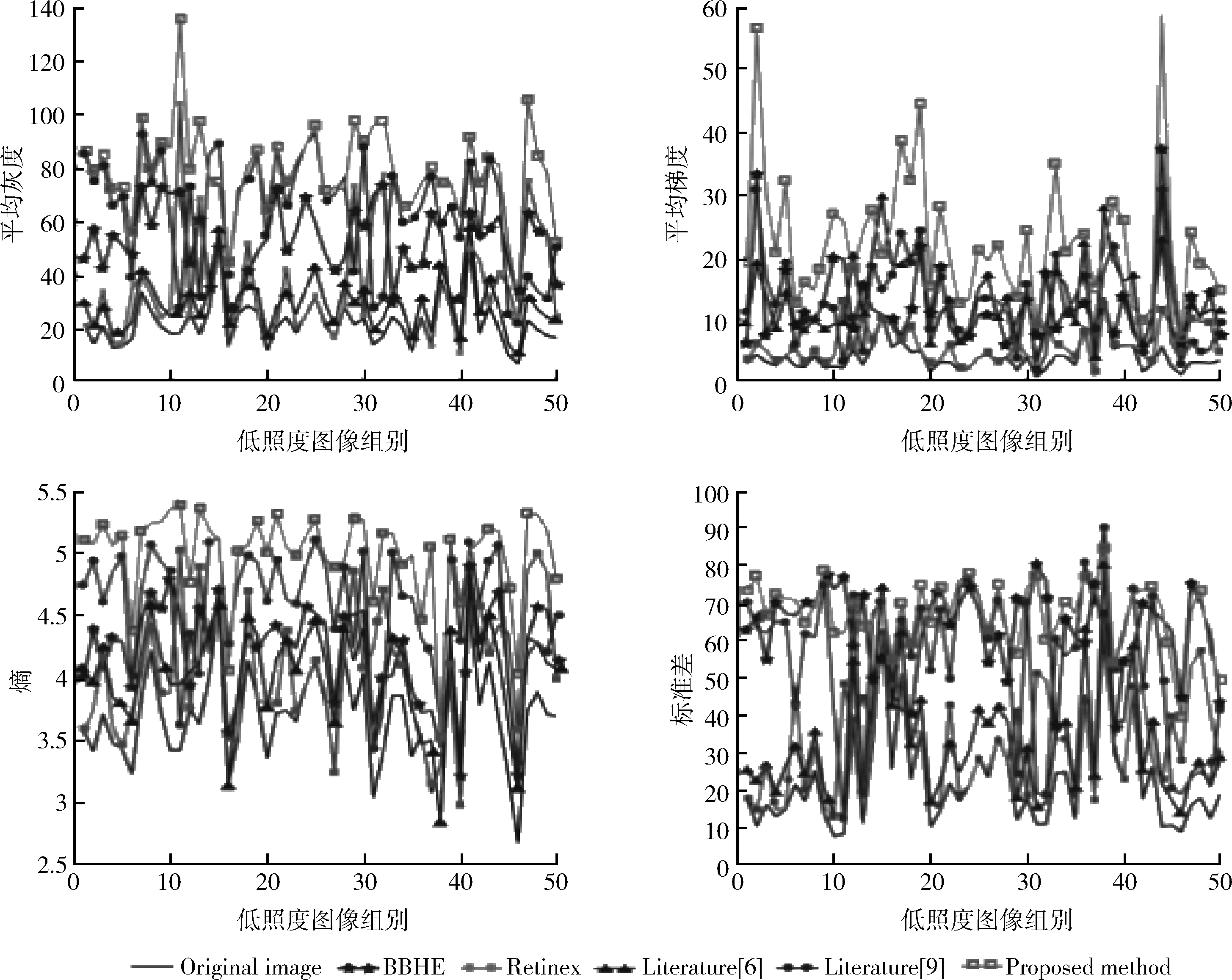
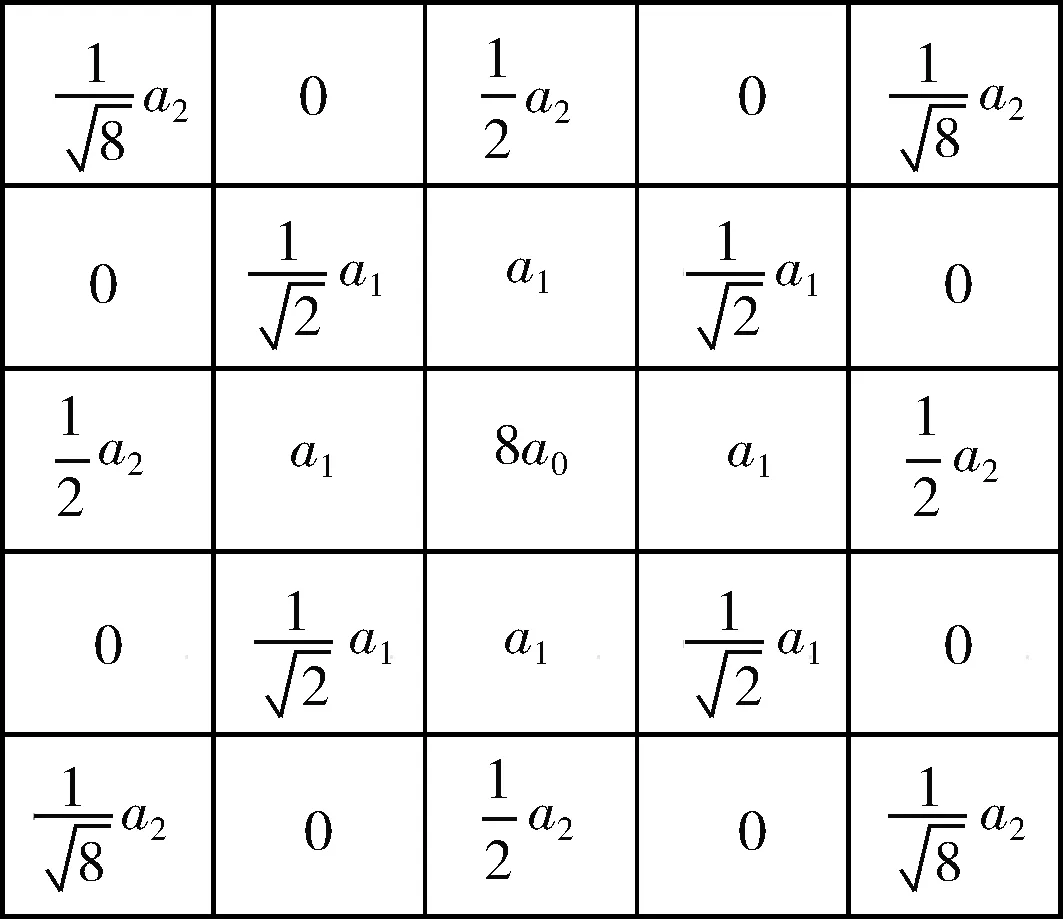
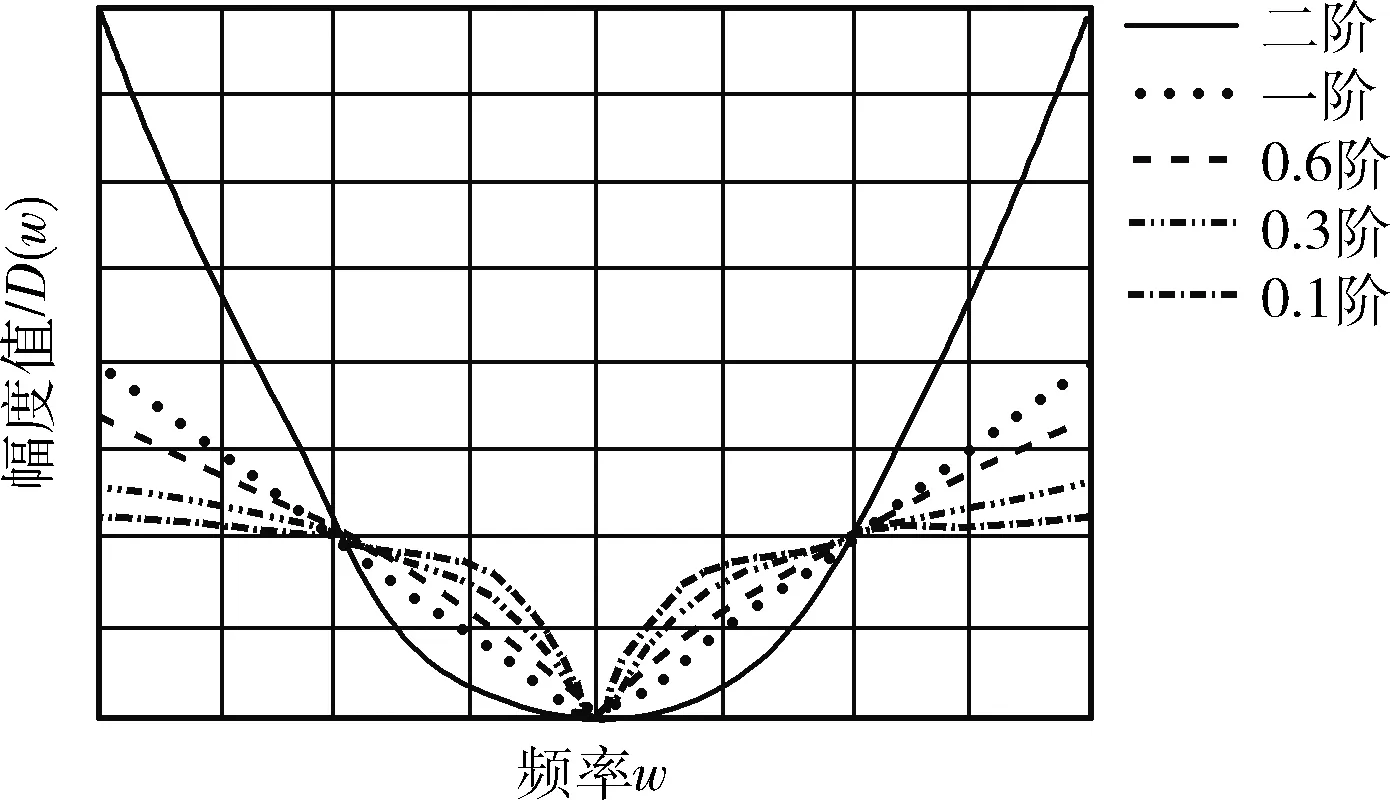
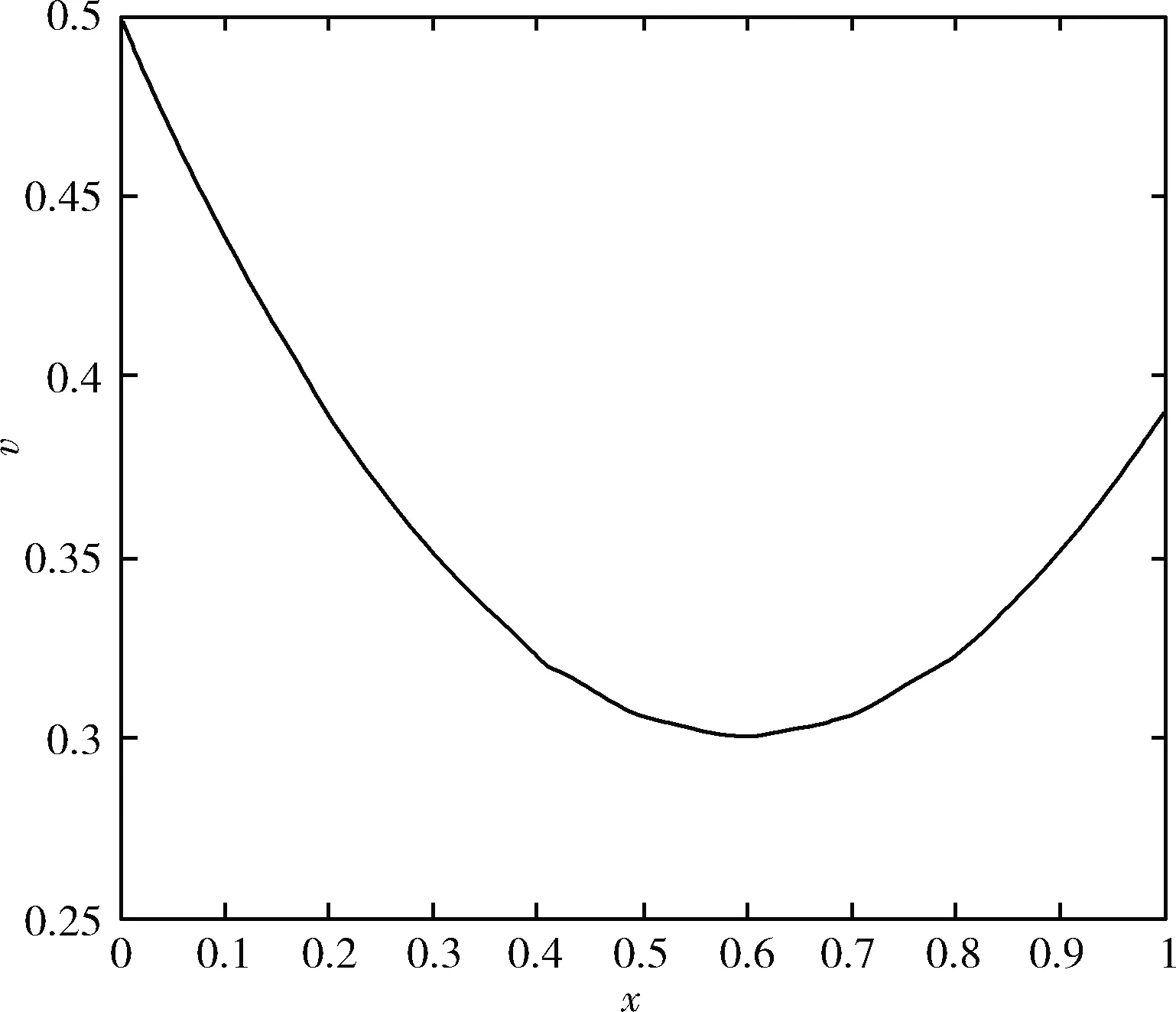
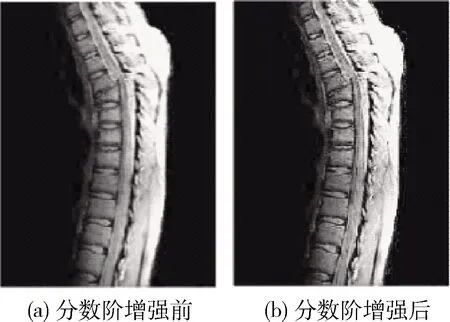
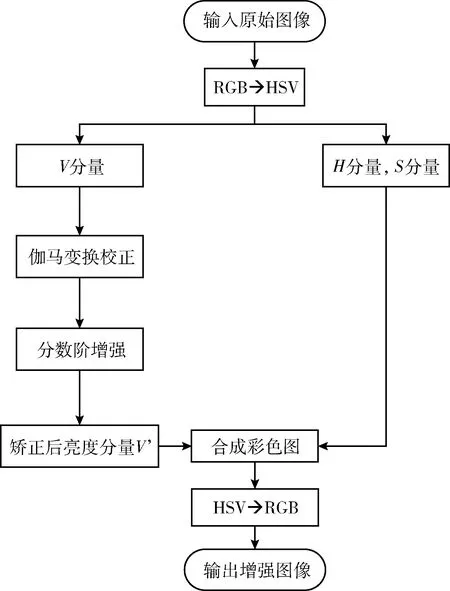
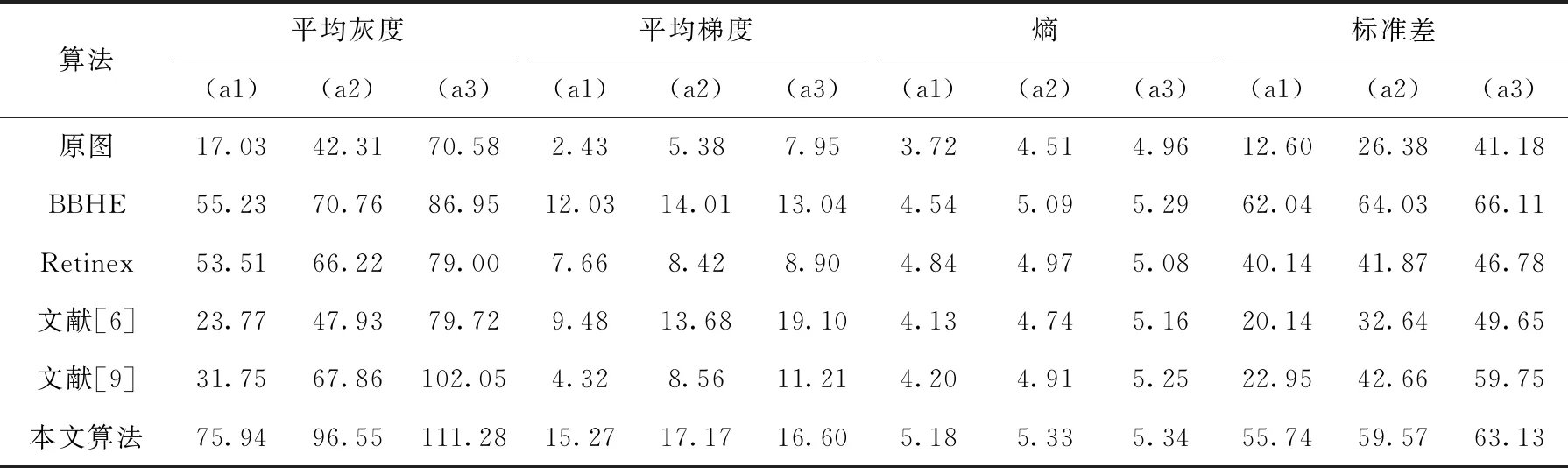
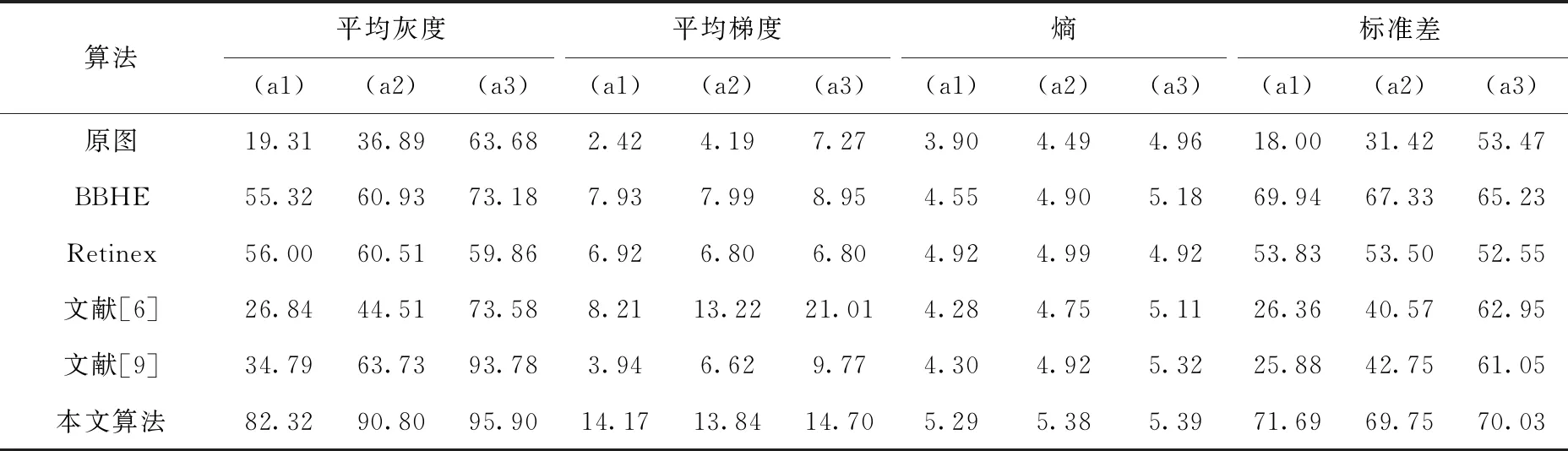
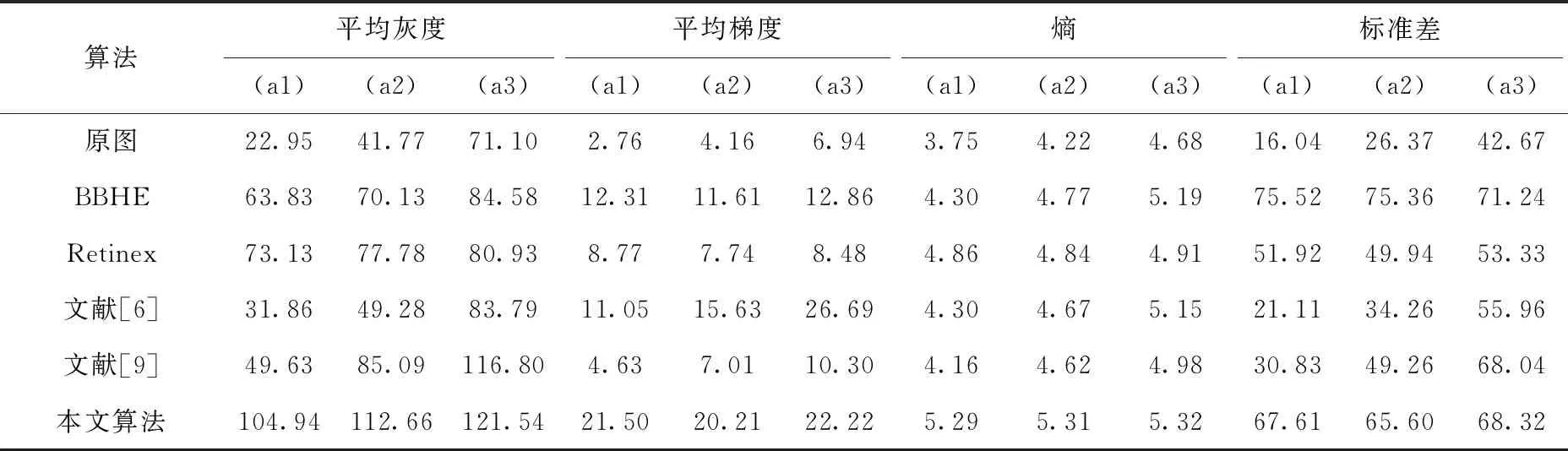
式中:x>0,a,x分别为积分下、上限,且x>a;m是满足m-1 当m=1,a=0时,式(12)改写为 (13) 将函数的取值区间[0,x]进行N等分,每分大小为Δx=x/N,令f0=f(0),f1=f(x/N),…,fk=f(kx/N),…,fN=f(x)。则由定积分定义可得式(13)的近似表达为 (14) 根据一阶导数差分格式,则有 (15) 根据式(15)写出方程右边的前n项系数 (16) 对图像进行分数阶微分增强主要是设计二维滤波器,对图像中像素点进行卷积运算。为使得到的模板具有较好的方向性,故利用分数阶微分相关系数构造8个方向的分数阶掩膜算子;本文依据邻域像素对中心点的不同影响设计了新的加权模板算子。具体方法是用像素点与中心点距离的倒数作为该点的权重系数,取相邻像素间的距离为1,则新的加权掩膜算子M如图3所示。 图3 加权掩膜算子M 为了使处理后的图像值不超过255,图3的掩膜算子在进行图像增强时先进行归一化处理。 分数阶微分增强中分数阶次的作用主要是控制增强的力度。不同阶次对图像高低频信息的具体影响如图4所示。 图4 信号微分的幅频 从图4可知,整数阶微分对高频信息部分有很强的提升作用,但是对于中低频部分会有削减。而分数阶微分虽然对高频部分的增强效果没有整数阶强,但是对低频部分的增强效果较好且不存在信息衰减情况。但现在很多分数阶次都是手动设置。因此,本文利用图像的局部信息x式(10)自适应确定合适的分数阶次。 一幅图像可分为3个部分:背景、纹理及边缘。图像中边缘梯度变化较大,像素间有明显差异,对于这部分信息并不是分数阶次越大越好,这样会造成边缘过增强,反而破坏图像。图像中较多细节信息处在纹理区,这部分表现为中低频,像素间差异不大,但是对于认知整个图像起着重要作用。因此,纹理区应该实现较大的增强,突出更多细节。背景区只需要进行非线性保留即可。从而可知,分数阶v与局部信息x之间的关系并不是单调递增关系。背景区取值较大,纹理区取值稍小,边缘区取值适中即可。因此,本文设计分数阶v与局部信息x之间的具体表现如下式 v=a*x2+b*x+c (17) 杨柱中等指出分数阶次在0.4~0.6效果较好,考虑到前期已对图像做伽马变换,图像信息在一定程度上已凸显出来,因此本文适当降低了分数阶次取值,将其设置为0.3~0.5之间。根据上述对背景、纹理及边缘的描述设置分数阶v与局部信息x之间的曲线如图5所示。 图5 分数阶次曲线 根据曲线图信息及一元二次函数相关性质求得a≈0.56,b≈-0.67,c≈0.5,则式(17)可以写成下式 v=0.56*x2-0.67*x+0.5 (18) 从式(18)可以得到,当局部信息x很小时,即为背景区时v取值稍大,实现非线性保留;当x较大,如最大取1,此时为明显的边缘时,v值不超过0.4。而一般情况下一幅图像的局部信息加权和最大在0.8左右,也就是在图像边缘已经很明显的情况下,分数阶次v的取值被控制在0.3左右,防止了过增强的情况出现。 确定v值后,利用图3加权掩膜算子M对伽马变换后图像G实现图像增强可用下式表示 (19) 对经过伽马变换后的图像图2(b)再进行分数阶增强的结果如图6所示。 图6 分数阶增强结果 从实验结果可以看出,经过分数阶增强后的图像视觉上更清晰,细节的表征更明显。 一般的彩色图都使用RGB彩色空间表示,但直接对RGB图像增强容易出现失真。HSV彩色空间比RGB彩色空间更加符合人类的视觉习惯[11]且分量间有较好的独立性。因此,将RGB图像先转到HSV彩色空间,对V分量增强后,再转回RGB彩色空间,具体的算法流程如图7所示。 图7 本文算法流程 为了验证文中提出算法的有效性,本文选取了多组图像进行实验,并且展示了每张图像在不同程度的亮度下的实验结果。同时将实验结果与BBHE算法、Retinex算法、文献[6]改进的分数阶增强方法、文献[9]带截断的改进伽马变换等进行对比,具体实验结果如图8、图9、图10所示。其中每组图像中的(a1),(a2),(a3)为不同亮度下的原始图,其它图像为使用不同算法的处理结果。如图(b1)~(f1)为相应算法对原图(a1)的处理结果;图(b2)~(f2)为相应算法对原图(a2)的处理结果。 图8 彩铅图像实验结果 图9 玫瑰图像实验结果 图10 建筑图像实验结果 由实验结果可知,BBHE算法易受原图的影响。Reti-nex算法得到了较好的增强效果且未出现失真现象。文献[6]对于亮度没有明显提升效果,而且分数阶次设计未充分考虑背景、纹理及边缘增强的特性,造成图像过增强,如图9中(d3)玫瑰花瓣处。文献[9]方法对图像亮度有明显的提升,且一定程度防止了过增强,但该方法在增强中未考虑原图亮度,参数选取也是全局的,因此不同亮度下结果会有明显差异。本文算法融合了伽马变换与分数阶,使该算法能同时达到亮度增强与细节增强的效果。伽马变换的参数和分数阶阶次都是自适应的,考虑了原始图像的亮度信息,还设置了抑制过增强的分数阶次函数。从各组实验结果的处理图(f1)、(f2)、(f3)可以看出,即使是不同亮度下的原图经过本文算法得到的增强图之间差异不明显,亮度上的提高也比前面几种算法好。自适应参数的设置比文献[9]全局设置拥有更好的效果,增强后的图像表现出了更多、更自然的细节,同时也未出现文献[6]算法中的过增强。 图像的平均灰度反映图像的整体亮度;平均梯度是图像清晰度的重要体现,能反映对细节的表达能力;信息熵可以体现图像所携带信息量的多少,表征的图像的复杂程度;标准差可以反映图像的对比度特征。为了进一步比较不同算法的处理效果,本文选取以上几个指标作为图像的质量评价标准。实验结果图8、图9、图10对应的评价数据见表1、表2、表3。 表1 图8不同算法实验结果的数据对比 表2 图9不同算法实验结果的数据对比 表3 图10不同算法实验结果的数据对比 分析表1~表3可知,所列算法都能达到增强图像的作用,使图像表现出更多的信息。但本文算法拥有较高的评价指标值,亮度较原图有较大的提升;梯度值的提升表明增强后的图像更清晰;熵值与标准差的提高,说明经过本文算法处理后的图像包含更多的细节。从表可知本文算法受原图影响最小,处理结果的各项指标值都很接近。即本文算法拥有较高的灵活性,对于亮度很低、特征表现不明显的图像,也能得到较好的结果。 为了进一步验证融合伽马变换和分数阶的低照度图像增强算法优于所列对比算法,随机选取了50幅低照度图片,并利用本文算法和对比算法对其进行处理,结果图片的各评价指标值域分布如图11所示。从图11可知,本文融合伽马变换和分数阶的低照度图像增强算法确实优于其它对比算法。 为了克服分数阶增强在亮度增强上的缺陷。本文提出了一种图像增强方法,该方法融合了伽马变换与分数阶,充分利用两者在亮度提升与细节增强的优势。实验结果表明,本文方法能很好的对低照度图像进行增强,进一步减少光照强度对原始图像的影响,使增强后的图像凸显出更多的细节。伽马变换中自适应参数的设置减小了算法受原始图像亮度的影响,具有较强的灵活性。在细节增强过程中新设计模板算子及分数阶次取值方式有效防止了过增强。不管是从视觉效果还是定量分析都展示出了本文算法的优势。如何在增强过程中有效去除噪声影响是下一步的研究内容。 图11 50组低照度图片实验结果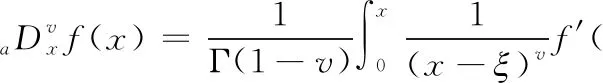
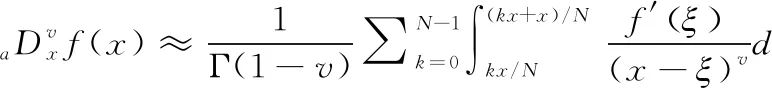
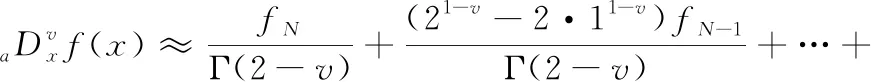
2.2 加权掩膜算子
2.3 自适应分数阶
3 算法实现
4 实验结果与分析
4.1 实验结果



4.2 客观评价
5 结束语