侦察吊舱电磁环境复杂度定量研究及软件仿真

吴阳勇， 李文海， 孙伟超， 王树友， 王向云

(1.海军航空大学，山东 烟台 264001； 2.中国人民解放军91395部队，北京 100000)

0 引言

在现代战场中，侦察吊舱的主要功能是对敌方雷达信号的截获、分选及对目标的方位识别，为飞行员提供告警信息，进而引导干扰吊舱正确工作[1-2]。在实际的作战过程中，吊舱必然处于复杂电磁环境中，其前、后向的多频段接收天线将会同时接收到各种背景信号和威胁源信号，而且由于不同任务的作战环境、作战对象和作战样式不同，其面临的电磁环境也是动态多变的[3]。

研究和描述吊舱所处的电磁环境，对进一步研究电磁环境对吊舱作战效果的影响，以及对提高吊舱战时的整体工作性能具有十分重要的作用，这也引起了国内外大量专家学者的关注[4]。代合鹏等[5]详细分析了电磁环境一般复杂度和特定复杂度的内涵，并提出了一种基于D-S证据理论的电磁环境复杂度定量分析方法来划分电磁环境的复杂度等级；李峥[6]提出熵可以作为电磁环境复杂度的度量方法；张斌等[7]提出了一种基于Shannon概率熵的复杂电磁环境的不确定性空间分析方法来描述电磁环境的复杂度。但是在过去的十几年里，熵作为电磁环境复杂度描述方法并没有得到很好的应用。

本文基于灰色理论[8]以及层次分析理论[9-10]提出了一种新的描述电磁环境复杂度的方法模型，结合组合论[11]给出复杂度等价互换公式以及等价过程需要的条件，并将算法编成软件，在后期的实例分析中发现算法达到了预期的要求。

1 复杂电磁环境度量指标选择

电磁环境的复杂度主要由两方面的因素形成：一方面是由战场上电子目标引起的复杂度，具有客观性；另一方面是由雷达对抗环境下产生的干扰信号引起的环境复杂度，具有主观性。文献[12]分析了复杂的电磁环境，从最常见的“四大域”(时域、频域、空域、能量域)出发，结合环境复杂度的主观性，给出了电磁环境复杂度计算模型。文献[13-14]给出了一个时变的功率谱模型，用于表征电磁环境任意一个空间在任何一个时刻点、频率值在单位面积以及单位时间内单位带宽通过的电磁环境的能量。

本文综合 “四大域”及主、客观性，从电磁信号的复杂度、密集性，以及干扰信号的复杂度出发选取了背景信号能量强度、辐射源信号的种类复杂度、方向偏离度、频率相似度和电磁辐射信号密度5个指标。

2 指标度量模型

2.1 吊舱电磁环境门限模型

设sc(t,f)为吊舱工作时的电磁环境功率谱密度， 吊舱的射频保护比即吊舱的环境门限模型S0，在连续条件下的表达式为

(1)

离散条件下，式(1)可以写为

(2)

式中：N表示吊舱工作的频率点数量，频率点离散地分为(f1,f2,…，fN)；f为接收信号的频率值；p是接收信号的功率。

2.2 背景信号能量强度复杂度模型

吊舱在复杂的电磁环境中，背景信号主要是指接收机接收到的信号电平的平均值大小。由于信噪比空间比较抽象，且现有的仪器测量信号的电平更加方便快速，所以针对背景信号能量强度建立的复杂度模型为

(3)

式中：ZVn′表征环境噪声电平越高，信号数量越多，复杂度越高；Vn′为吊舱接收机接收信号的平均电平；S0为噪声环境对接收机产生干扰的最低平均电平，即接收机电平门限值；下标n′为可被仪器识别的信号种类的数量。

2.3 辐射源信号的种类复杂度模型

在一定的空域中，背景信号的种类越多，信号的体制越复杂，则对吊舱的影响越大，其电磁环境复杂度就越高。在实际操作过程中，吊舱在正常工作情况下可识别的信号种类为M0，最多可以识别的种类为Mmax，M为当前吊舱识别的信号种类数量，则基于辐射信号的种类复杂度模型可以表示为

(4)

2.4 方向偏离度复杂度模型

方向偏离度[15]具体是指环境目标辐射源信号的方向与吊舱接收机接收天线正对方向之间的偏离程度，偏离程度越小，说明方位的重合度越高，引起的环境复杂程度越高，复杂度模型为

(5)

式中：Gr为吊舱接收机信号目标方向上的接收增益；Grj(θ)为吊舱在辐射源信号方向上的信号增益。

2.5 频率相似度复杂度模型

频率相似度表示吊舱工作频率与电磁环境中的信号频率的接近程度，空间中的电磁信号频率越接近吊舱工作频率，则环境信号对吊舱的干扰就越大，复杂程度就越高，给出频率相似度模型为

(6)

式中：U(f)是以频率为变量的阶跃函数。

Δfr=fr,max-fr,min

(7)

fmax=min[fr,max,fs,max]

(8)

fmin=max[fr,min,fs,min]

(9)

其中：fr，max为吊舱接收机带宽的最大值；fr，min为吊舱接收机带宽的最小值；fs，max为空间中辐射信号带宽的最大值；fs，min为空间辐射信号带宽的最小值。

2.6 电磁辐射信号密度复杂度模型

在复杂的电磁环境空间中，吊舱接收机天线在单位频段范围内接收到信号的数量越多，则对装备来说由此带来的环境复杂度就越高，可以建立复杂度模型为

(10)

式中：ρ0为实际电磁环境信号密度；ρ为吊舱可承受信号密度的极限。

3 灰色层次分析法在复杂度评估中的应用

3.1 层次分析法获取评估模型

层次分析法(Analytic Hierarchy Process，AHP)是对一些较为复杂、较为模糊的问题做出决策的简易方法，特别适用于那些难以完全定量分析的问题[10，16]。

3.1.1 建立层次结构模型

本文将问题分为两个结构层——目标层和指标层。把研究对象电磁环境复杂度作为目标层，上文中评估这一目标的5个指标作为指标层。

3.1.2 构造判断矩阵

上述层次结构中体现出的仅是指标和目标之间的关系，但是各个指标在得到目标的过程中表现出来的比重并不是一样的。仅通过决策者的主观判断往往是不够的，所以需要将指标进行量化处理，就需要构造判断矩阵A，用于表示指标层n个因子X={x1,x2,…,xn}对目标层复杂度Z影响的大小比值。每次取两个因子xi和xj，矩阵A中的任意一个数值aij表征xi和xj对Z影响大小的比值，且容易得到反过来xj和xi对Z影响大小的比值aji=1/aij。

用1～9及其数值的倒数作为标尺即aij的值，具体含义如表1所示。

表1 判断矩阵标尺含义

得到判断矩阵A的表达式为

(11)

3.1.3 指标层权重及一致性检验

针对环境复杂度影响因素指标层的权重问题，在层次分析法中求得判断矩阵A的最大特征值λmax及各因素对应的权重向量W=(w1w2…wn)T。

对于指标层因子复杂度影响度比较，不同专家或实验人员的标准是不一样的，评判时会存在误差，为了提高判断矩阵A的权重可靠性，下面进行一致性检验。

检验过程为

(12)

式中：n为指标层因子的个数，即矩阵的阶数；λmax为矩阵A的最大特征值。当n较大时，修正指标为

(13)

式中：RI为修正因子，文献[10]给出了相应的值，如表2所示。

表2 RI 的值

由式(12)和式(13)可求得，当修正指标CR<0.1时，可以认为矩阵A的元素(权重因子)是满足一致性的，可以进行下一步指标矩阵的建立。

3.2 灰色综合评估模型

灰色理论分析的对象首先必须是一个客观存在的事物或系统，在这个系统中那些随机变量、无规则的干扰成分被看成是在一定变化范围内的灰色量，可以通过一定的数据处理，将灰色量变为生成数，进一步得到具有一定规律的数据模型。

将吊舱所在的复杂电磁环境看作是等待分析解决的灰色系统，通过灰色系统分析理论得到灰色综合评估模型，具体分析过程步骤如下。

1) 确立专家评估矩阵。假设在吊舱环境复杂度评估过程中，指标层有n个影响因子，有m位评估专家进行指标评估，将影响因子依次编号为1,2,…,n，专家依次编号为1,2,…,m，可得到评估矩阵为

(14)

式中：eij表示编号为j的专家对编号为i的影响因子的评估值。

2) 定义评估灰类。吊舱复杂电磁环境的评估灰类就是其复杂度的白化权函数，而根据不同的灰数，白化权函数可分为4类，分别用h1(eij)，h2(eij)，h3(eij)，h4(eij)表示，用9，7，5，3分别表示电磁环境复杂度等级为重度复杂、中度复杂、轻度复杂、可忽略4种标准，不同的灰数区间对应的白化权函数的具体表达式分别为

(15)

(16)

(17)

(18)

3) 计算复杂度灰类为k(k∈1,2,3,4)指标层影响因子为i(i=1,2,3,4,5)的灰色评估系数，分别得到评估权重系数及总评估权重系数为

(19)

(20)

(21)

式中：n为指标层影响因子数；k为灰类数。

4) 得出综合评估F=A·Q；归一化评价结果P=WT·F·(9753)T。

4 指标层影响因子复杂度等价互换原理

如果需要对电磁环境细化分析，更深入地了解其他指标对环境复杂程度的影响，那么需要的计算量是呈指数上升的，对于实际工程来说，有些参数是较难准确测量得到的，实现起来困难较大，也会浪费大量的资源，如果影响因素之间存在线性关系，能用现有的数学表达式表示出来，则通过组成论中的理论推导出的指标因素引起的环境复杂度之间是可以等价互换的，用简单易测量的方案等价反映复杂因子，可大大减少计算量和模型的数量，工程上也更容易实现。以环境中辐射源与吊舱的相对位置及可被识别速度两个因素为例，具体推导过程如下。

将吊舱周围的雷达对抗环境中所有雷达信号看成一个广义的集合Z(s)，集合中假设有N′种雷达信号，分别编号为1，2，…，N′。ai代表第i种雷达信号的名称，bi为对应ai的雷达信号数，则可以将该集合写成

(22)

假设函数f(x)表征式(22)辐射源信号集合Z(s)的概率密度分布函数，M为集合中信号的总数。当x∈[a,b]时，侦察吊舱周围的电磁环境复杂度可表示为

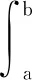
(23)

可以假设两个集合Zl(y)和Zv(x)分别表示辐射源信号位置集合以及可识别速度(可被机载吊舱分辨的速度)集合的复杂度，两个集合的组成元素分别为(y1,y2,…,yn)和(x1,x2,…,xn)，均存在n个变量。假设函数h为x变量和y变量之间的映射关系，具体关系为

(24)

在高等数学中假如hi的一阶偏导数是连续的，那么它所对应的雅可比行列式是不能等于零的，具体表达式为

(25)

假设存在函数Fl=(y1,y2,…,yn)和Fv=(x1,x2,…,xn)分别为Zl(y1,y2,...,yn)和Zv(x1,x2,…,xn)的概率密度分布函数，由雅可比行列式的含义以及x和y之间关于h的转换关系，可得到Fl和Fv的关系为

(26)

由上文可知，Zl(y1,y2,…,yn)和Zv(x1,x2,…,xn)分别表示辐射源信号位置集合以及可识别速度(可被机载吊舱分辨的速度)集合的复杂度，则可得到

Zl(y1,y2,…,yn)=Zv(x1,x2,…,xn)+M·ln|β| 。

(27)

假如在侦察吊舱复杂的电子战环境中，辐射源信号的位置信息y与可识别速度信息x之间存在某种线性关系，即y=cx，c为整数，那么可以进一步得到Zl(y)关于Fv(x)及x的关系式为

(28)

假如c为正整数，即c>0，则有

Zl(y)=Zv(x)+Mlnc。

(29)

当位置信息变量y与可识别速度信息变量x之间符合上述的线性关系，在集合关系上相当于平移的关系，它们之间的雅可比行列式β≡1，则有

Zl(y)=Zv(x)

(30)

表示当两个针对吊舱电磁环境复杂度的因素符合一定条件时，它们引起的复杂度程度是可以等价、互相交换的。那么在复杂的空中电磁环境中，可以通过分析主要电磁辐射源信号之间的关系，实现在实际工作中无法测量的影响因子，为建立真实的电磁环境找到了更加方便的途径，同时也减轻了相关数据采集与处理的工作量。

5 实例分析

为了证明所提方法具有实际的意义，考虑现实条件，进行了一些情景假定。

假定1 某机载电子干扰吊舱在某个电磁空间里识别信号的种类为5，该吊舱正常工作可识别4种类型信号，最多可识别8种信号，则由式(4)可得到辐射信号的种类复杂度Zm=0.55。

假定2 吊舱工作频率范围为70～100 MHz，即Δfr=30 MHz；空间中各种辐射源信号频率范围为55～80 MHz,由式(6)可以得到频率相似度复杂度Zfr=0.5。

假定3 吊舱天线与辐射源信号的方向偏离度(因为吊舱天线的实际接收发射信号增益与方向变化关系式已知)以及背景信号能量强度，包括吊舱接收机接收信号平均电平Vn及噪声环境对接收机产生干扰最低平均电平S0，在实际的工作中可以通过仪器测量出来。假定实际工作时方向偏离度为0.43,测得Vn=3.2S0，即背景信号能量强度复杂度ZVn=0.69。

假定4 仪器测得吊舱承受信号密度的极限系数为105，实际电磁环境信号密度系数为6300，则Zρ=0.63。

指标层影响因素比较对照表1可得表3及矩阵A(注：表3数据为纵坐标逐一与横坐标影响程度的比值)。

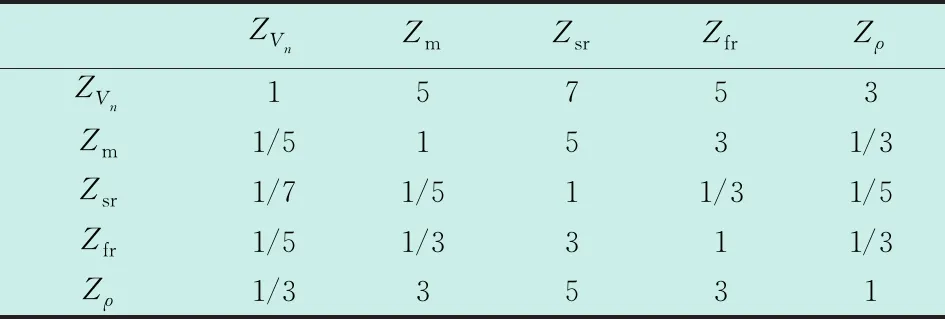
表3 指标层影响程度比较值

由Matlab计算可得到矩阵A的最大特征值λmax=5.318 5，以及指标权向量W=(0.536 40.156 80.043 90.087 70.262 1)T，由式(13)和式(14)及表2可得CI=0.08，一致性检验结果CR=0.07<0.1，满足一致性检验。

则由权值矩阵Q可得到最终的度量结果:P=WT·Q=(0.249 30.273 20.309 40.254 7);则电磁环境复杂度评估结果为：P最终=P·(9753)T=6.47，在5～7之间，由此可以得出结论：此时的电磁环境复杂度为中度复杂。

6 复杂度评估算法软件仿真

侦察吊舱电磁环境复杂度评估软件主要功能是实现算法的软件化及历史数据的评估，即将上述环境参数以TXT文件形式存储，通过软件进行计算并输出对应的复杂度。具体评估流程见图1。

图1 电磁环境复杂度评估流程

图2为复杂度度量用户界面，分为环境数据输入模块、数据输入样式、仿真计算及其结果模块。

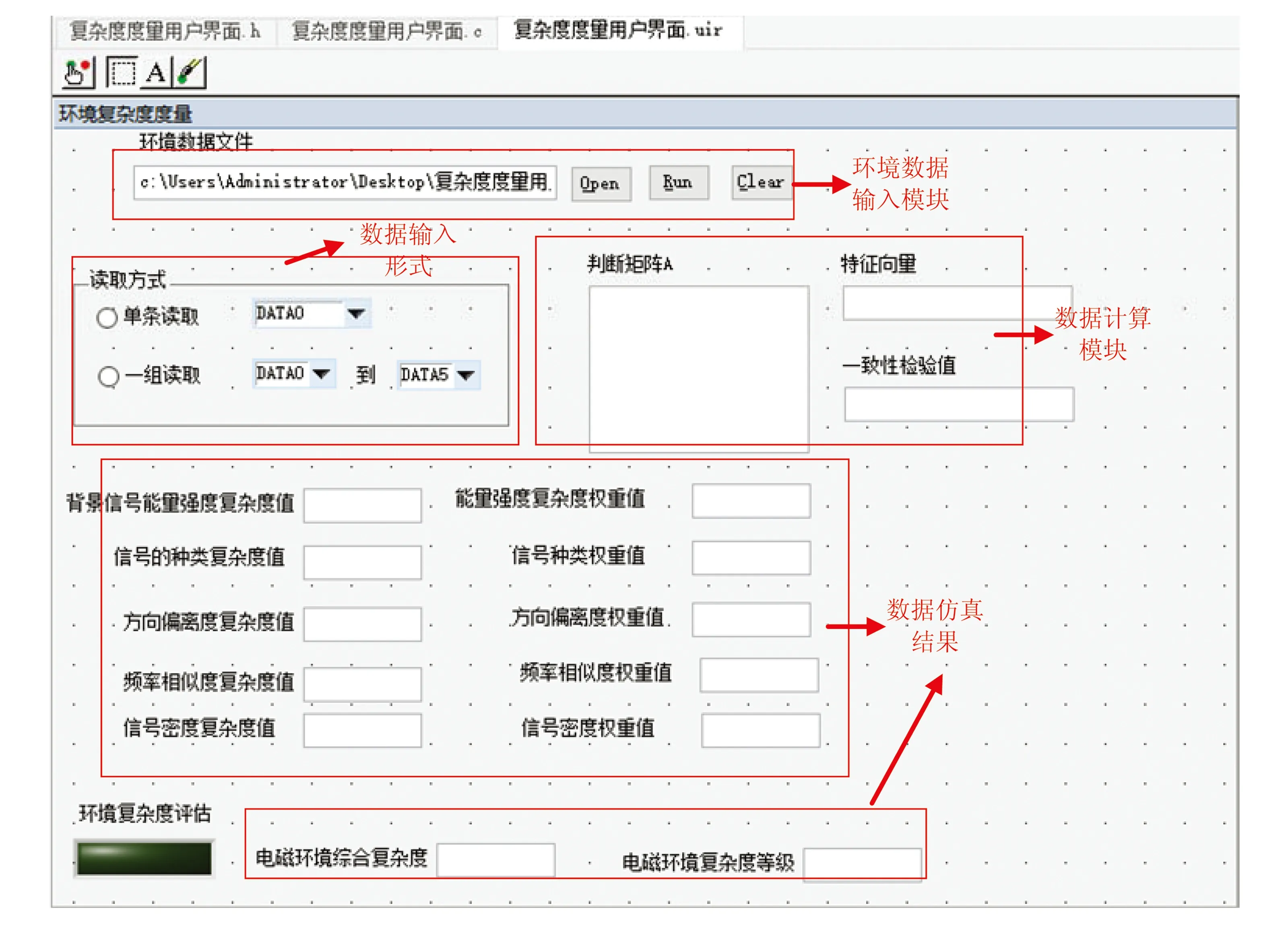
图2 复杂度度量用户界面

基于软件平台LabWindows CVI，第4章中典型的电磁环境仿真结果如图3～图4所示。

数据输入模块分为数据导入文件、数据仿真Run及仿真界面还原3部分。图3为典型环境数据的TXT具体存储样式。

图4为第4章中电磁环境数据DATA0的软件仿真结果，与模型计算结果在误差范围内，仿真结果是符合要求的，复杂度仿真软件具有一定的使用价值。

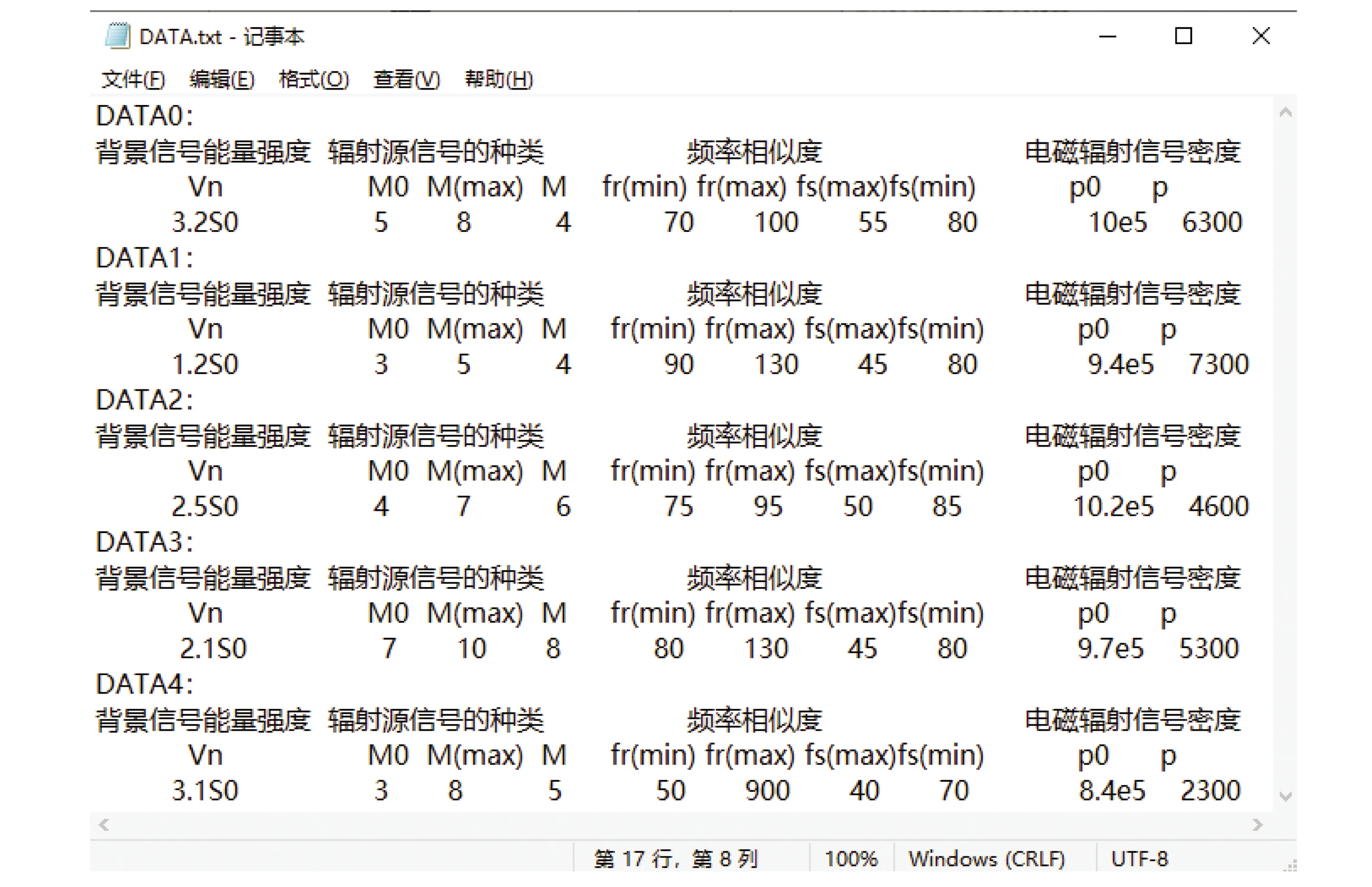
图3 电磁环境数据存储样式

图4 复杂度计算仿真结果

7 结论

本文针对吊舱复杂的电磁环境度量问题，将层次分析法和灰度理论相结合，经历了指标因素选择、判断矩阵、专家矩阵建设、评估矩阵及指标权重的计算，并且基于LabWindows CVI设计了一个简单的复杂度度量软件，将算法写入软件得到了较好的仿真结果，最终解决了复杂度度量问题。该方法不足之处是主观判断和客观相结合具有一定的误差。最后通过实例验证其实用性，动态环境变化与等价互换原理相结合进行复杂度研究将是下一步的工作方向。