双雷达联合测速系统研究

顾 明，周 媛，刘亚奇，郑广瑜

（1.上海申通地铁集团有限公司技术中心，上海 201103；2.上海无线电设备研究所，上海 201109；3.上海市目标识别与环境感知工程技术研究中心，上海 201109）

1 引言

轨道交通具有运量大、占地少、单位运量能耗小等诸多优点，因此世界各国均将其作为综合交通系统建设的重点[1-5]。

列车自动控制系统（ATC）是以技术手段对列车运行方向、运行间隔和运行速度进行控制，以实现其安全、高效运行的系统。随着轨道交通列车运行速度的大幅提升、行车密度的不断提高及追踪间隔的逐渐缩短，行业对于ATC系统及其核心设备的安全性、可靠性及精确性要求日益增长[6-9]。该系统需要实时、精确地获取列车运行速度及位置信息，以实现对运行过程的精细化控制。而高精度自主测速传感器是该系统的核心传感器之一。其中，雷达测速系统具备精度高、受环境影响小、价格低等优点，有突出的技术优势[10-12]。

然而，目前的雷达测速系统多采用单部雷达测速，由于雷达天线相位中心与天线几何中心通常不重合，因此确定雷达垂直高度存在很大困难。此外，对于不同线路、不同列车及不同雷达安装位置，都需要进行相应的雷达天线相位中心高度测量。为解决上述问题，本文探索采用2部雷达进行双视角、双波束探测，并利用2部雷达测得的数据联合解算列车速度；并考虑到实际工程应用对于系统质量、尺寸以及可靠性的要求，采用高性能高集成硬件电路设计，从而提升系统对应用环境的适应性。

2 双雷达联合测速原理

2.1 雷达测速基本原理

物体辐射的电磁波频率因为波源和观测者的相对运动而产生变化，这种现象被称为多普勒效应。雷达测速法就是利用这一效应测量列车运行速度。测速雷达安装在列车车底，雷达天线以一定的角度向轨面发射电磁波，电磁波经轨面反射回天线，如图1所示。由于雷达随列车产生相对于轨面的运动，因此发射波和反射波之间存在一定的频率差（即多普勒频移量）。如果列车处于前进状态，反射波频率高于发射波频率；反之，则低于发射波频率。列车运行速度越高，多普勒频移量越大。通过测量此频移量便可计算出列车的运行方向和即时运行速度。多普勒频移量fd的计算公式如下：

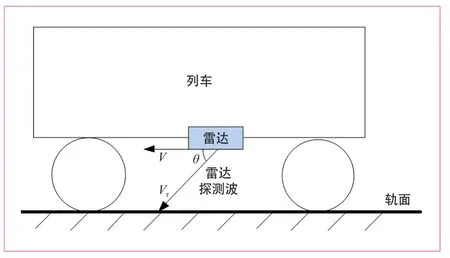
图1 雷达测速示意图

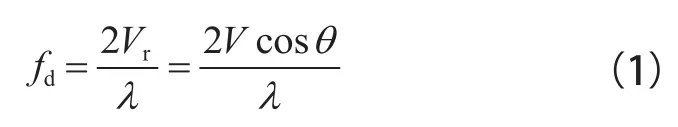
式（1）中：λ为雷达波波长；θ为雷达天线与轨面的夹角（雷达波发射角）；V为列车相对于轨面的行驶速度；Vr为雷达相对于轨面的径向运行速度，是V在雷达水平面上的分量。

在测速过程中，雷达天线不是垂直于地面，而是与地面呈一定的夹角。列车在运行时会不可避免地产生颠簸振动，尤其是遇到坡道或者弯道等复杂路面时，而颠簸振动会使雷达天线与地面之间的夹角发生改变，雷达垂直高度H随之变化，从而导致极大的测量误差。针对列车颠簸引起的测速误差大的问题，可在雷达测速传感器内配置2个互成角度的微波模块，通过对其采集的信号进行分析和处理，实现角度误差补偿，如图2所示。

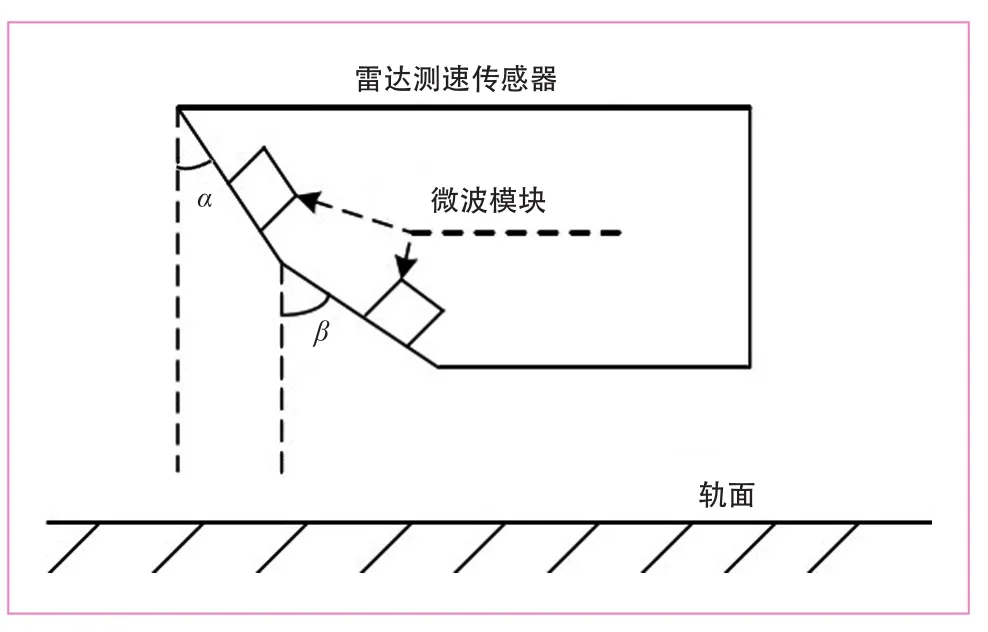
图2 雷达探测角示意图

2.2 双雷达联合测速

为解决单部雷达测速时因列车振动导致雷达垂直高度H产生误差，使测速精度偏低的问题，本文提出双雷达联合测速方法，即利用2部雷达同时进行相关参数测量，然后根据测得的2部雷达垂直高度差及多普勒频移量对单个雷达垂直高度进行解算，进而求解列车速度。这种方法只需测量2部雷达的垂直高度差，无需分别测量各雷达垂直高度，可消除雷达垂直高度的标定误差及列车颠簸引起的测量误差。

双雷达联合测速的计算方法如下。

设2部雷达的垂直高度分别为H1和H2；雷达1测得的斜距为R1，测得的多普勒频移量为fd1；雷达2测得的斜距为R2，测得的多普勒频移量为fd2。

根据图3所示的几何关系可以得到如下2个多普勒方程：

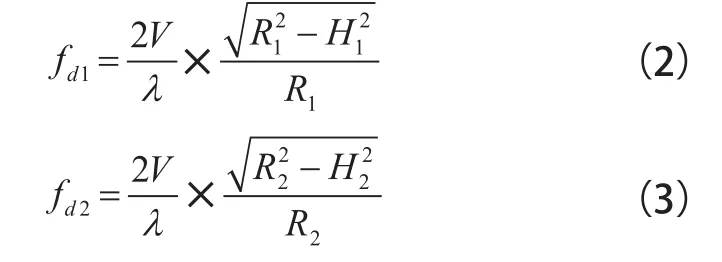
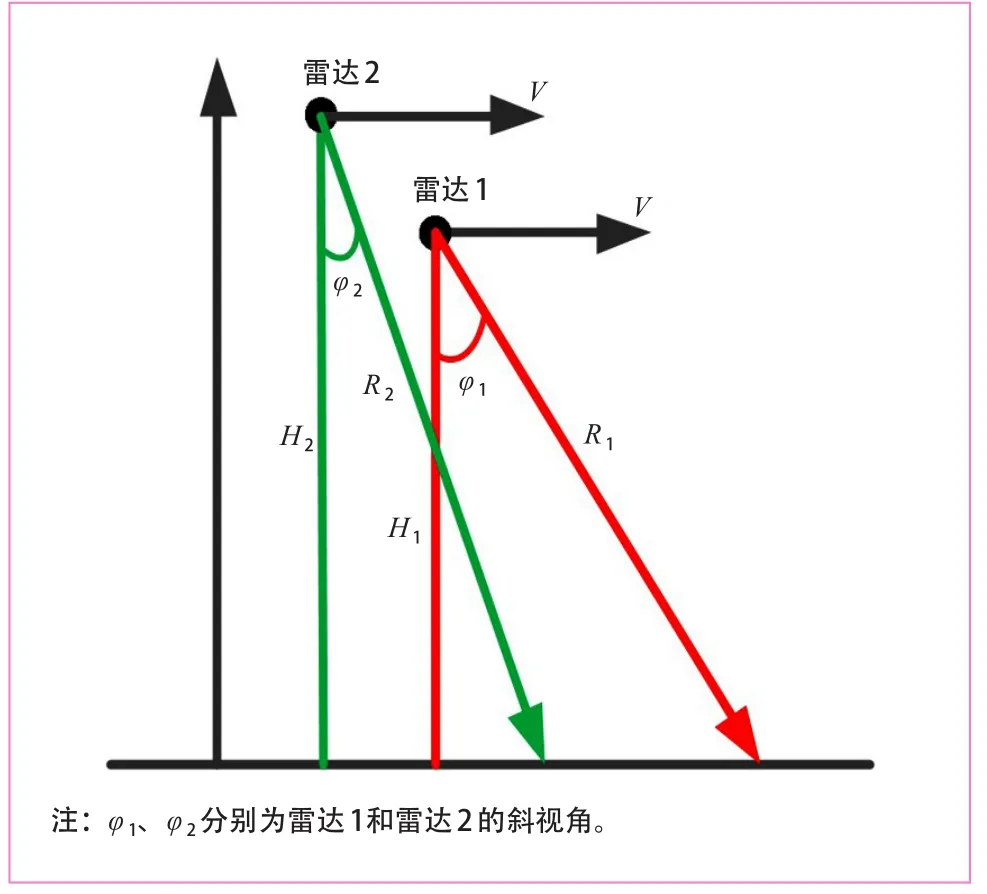
图3 2部雷达联合测速几何关系

假设2部雷达高度差已知，则式（3）可以表示为

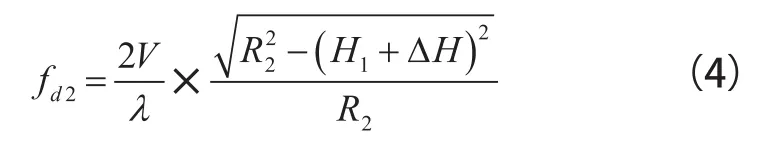
由于2部雷达测量的速度相同，联立式（2）和式 （4）可以得到

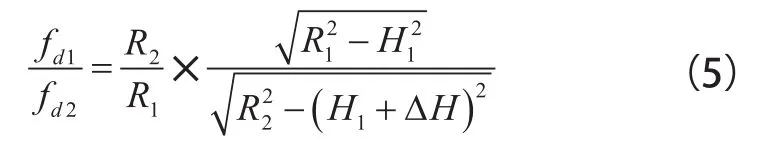
通过求解式（5）即可得到雷达1的高度H1，进而得到雷达2的高度H2。将解算得到的雷达绝对高度H1或H2代入式（2）或式（3）即可解算列车速度。

3 双雷达联合测速系统构成及优点

双雷达联合测速系统采用雷达1和雷达2两组收发通道，收发天线分置。2部雷达除调频斜率互异外，调频带宽、脉宽、调频率等参数完全一致；两者独立工作，在加电后分别接收信息处理板指令，并同时进入测距测速模式，其发射天线分别发射经信号波形调制的、正交的大带宽线性调频连续波信号，接收信号时采用去斜接收的方式，以此提高系统的鲁棒性和可靠性。系统原理框图如图4所示。

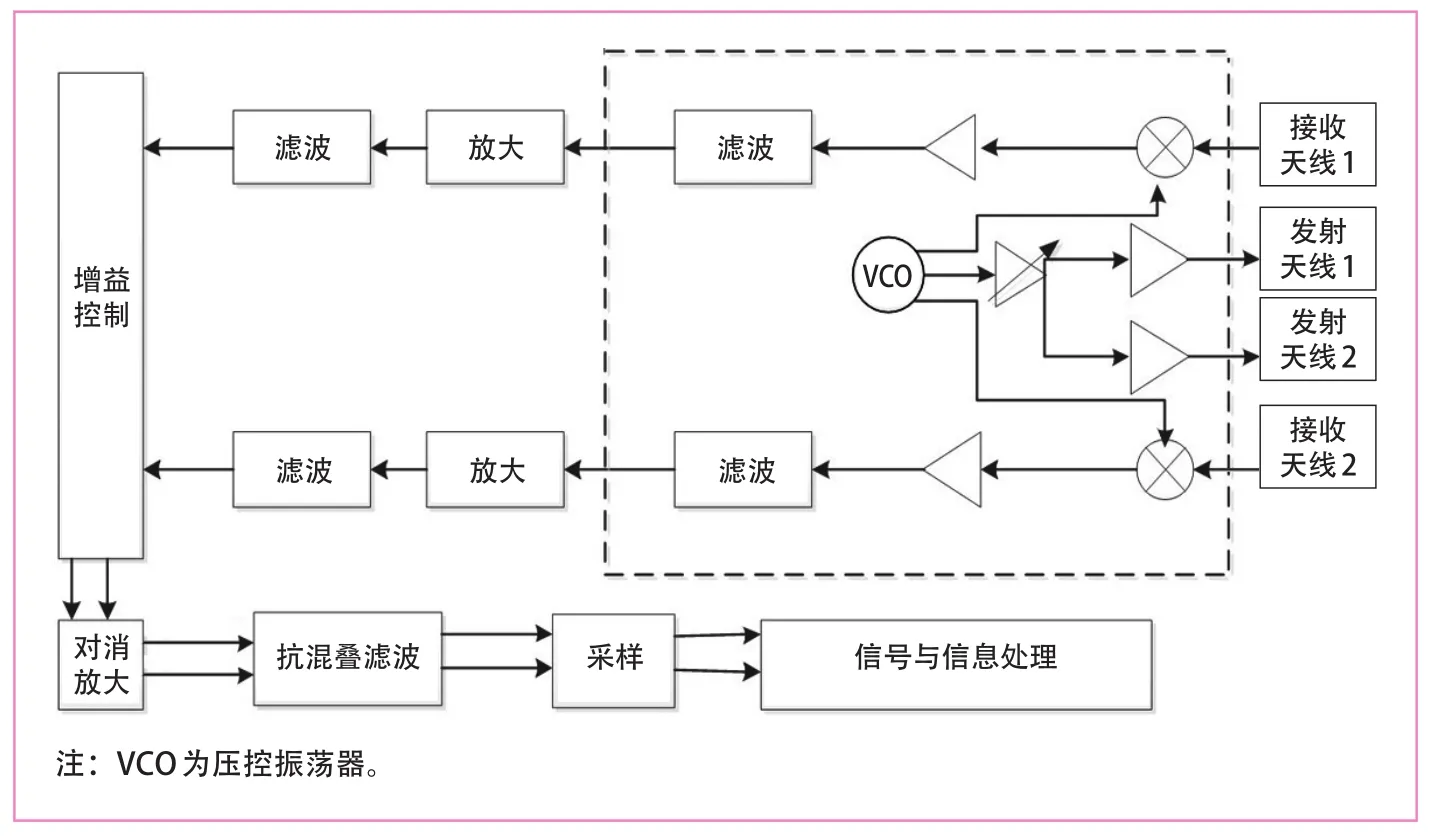
图4 系统原理框图

天线采用微带阵列天线，其具备主瓣宽度窄、方向图可赋形、交叉极化电平低的特点。主瓣宽度窄可提高天线的定向辐射能力，使其满足苛刻的环境需要。微带天线易于集成，可实现在一块介质基片上承载整个天线和馈电系统的目标，且具有体积和质量小的优点。此外，天线利用印制电路板（PCB）等成熟的工艺技术加工而成，这些工艺的精度远高于金属波导的制作和开槽工艺。

在硬件组成方面，收发天线、微波探测前端、信号与信息处理单元、电源采用集成设计，将其集成到1块电路板上，以减小系统尺寸和质量。鉴于当前单片集成电路（MMIC）应用条件的日趋成熟，以及当前实验条件的限制，采用微带混合集成电路和MMIC相结合的信号产生方式。MMIC芯片的使用可以最大限度地减小系统的体积，降低其设计复杂程度。此外，MMIC芯片也易于实现数字控制，可通过接口对其进行控制，从而实现高性能高集成的硬件电路设计及系统的优化。因此，MMIC可满足系统对质量、尺寸以及可靠性的要求。

4 系统测速精度分析

本章将从影响测速精度的2个误差因素（即多普勒频移量估计误差、雷达垂直高度偏差）出发，对双雷达联合测速系统与其所含单部雷达的测速精度进行对比分析。

4.1 多普勒频移量估计误差

多普勒频移量估计误差Δfd与雷达测速误差ΔV之间的关系为：

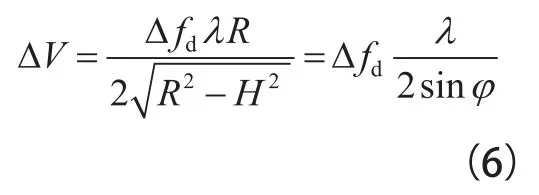
式（6）中，R为雷达测得的斜距；H为雷达垂直高度；φ为雷达斜视角。由式（6）可知，对于单部雷达测速系统，当φ不变时，ΔV与Δfd成正比关系。图5是双雷达联合测速系统及其所含各雷达（高雷达垂直高度为距轨面0.95 m、低雷达为0.8 m）的测速仿真计算结果。由图可知，雷达测速误差随着多普勒频移量估计误差的增大而增大，且当多普勒频移量估计误差相同时，安装位置较高的单雷达（以下简称“高雷达”）相比位置较低的单雷达（以下简称“低雷达”）测速误差更小，而双雷达联合测速系统的测速误差较任意单部雷达更小且波动较小，曲线较平稳。

图5 多普勒频移量估计误差导致的测速误差

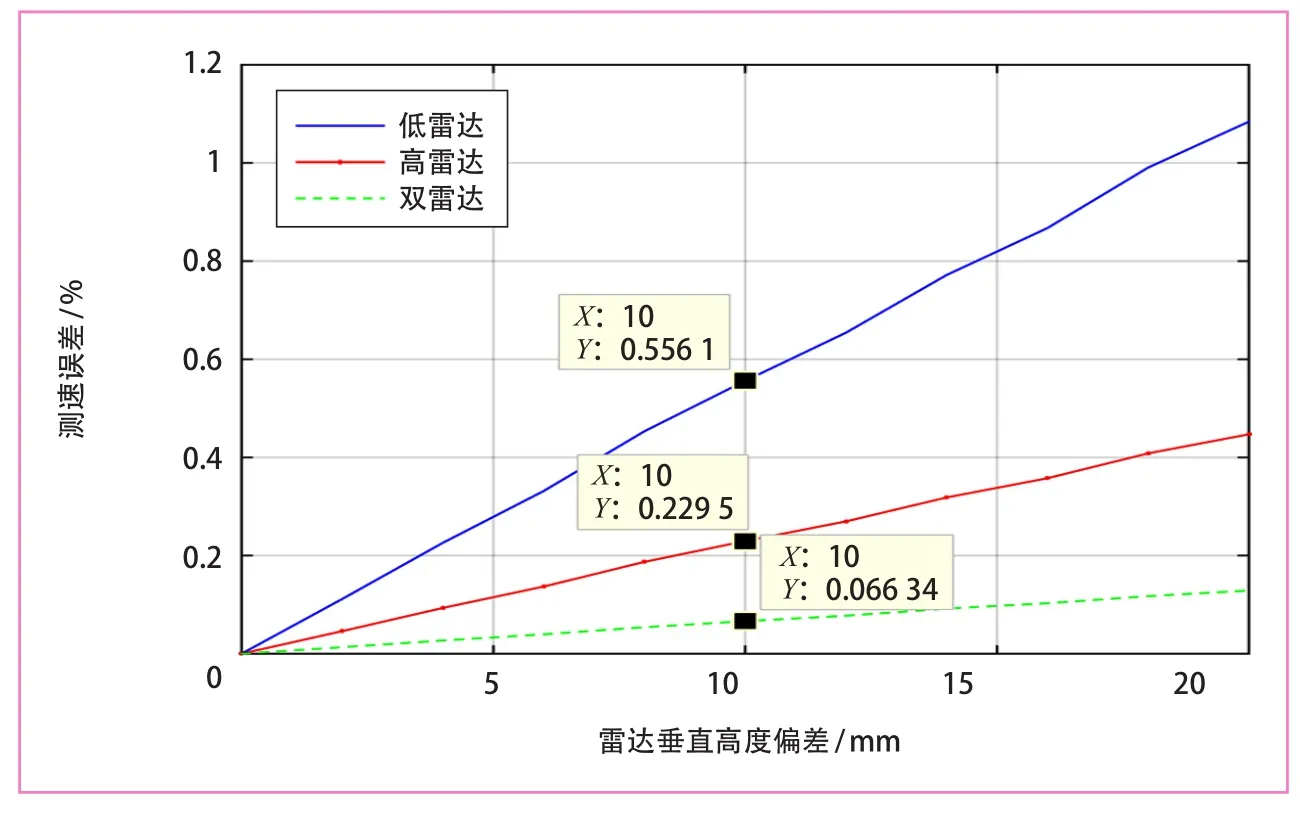
图6 雷达垂直高度偏差导致的测速误差

4.2 雷达垂直高度偏差

由式（2）或（3）可知，单部雷达测速首先需要精准地测量雷达垂直高度。然而，实际上雷达天线的相位中心通常并不是天线的几何中心，且列车在运行时会不可避免地产生颠簸振动，致使雷达垂直高度H随之变化，从而导致极大的测量误差（图6）。由图可知，雷达测速误差ΔV随雷达垂直高度偏差的增大而增大，且在低雷达上体现得尤为显著。正常情况下，列车垂向位移在cm量级时，ΔV可达到0.5～1 cm /s量级；在斜视角φ为55°的条件下（注：雷达垂直高度越低，φ越大），ΔV将放大到1.42倍，达到1.5 cm /s量级；在φ为65°的条件下，ΔV将放大到2.14倍，达到2 cm /s量级。考虑到低雷达与高雷达的安装高度分别为0.8 m和0.95 m，其仿真测得的最大测速偏差可达到1.3%。而双雷达联合测速系统只需测量2部雷达的垂直高度差，无需测量单部雷达的垂直高度，因此可减小单部雷达测速时因垂直高度偏差引起的标定误差。

5 试验验证

为对双雷达联合测速系统的精度和稳定性进行试验验证，将本系统及市面上的一款高精度（测速范围0.5～500 km/h内的误差＜0.2%）进口激光测速系统（哈斯勒Corrail 1000）安装在一列地铁试验列车上，并分别对比其在列车最高运行速度为60 km/h和80 km/h时，以及在加速阶段和减速阶段4种工况下的测速结果。

图7a和图7b分别为双雷达联合测速系统与激光测速系统在列车从静止状态启动，到维持最高运行速度60 km/h或80 km/h一段时间，再制动至停止的过程中的测量结果对比图，图7c和图7d分别为2个系统在列车加速和减速阶段的测量结果对比图。由图可知，双雷达联合测速系统与激光测速系统的测量结果基本吻合，且波动更小；双雷达联合测速系统具有较高的精度和稳定性，在一定速度范围内可达到进口激光测速系统的水平。

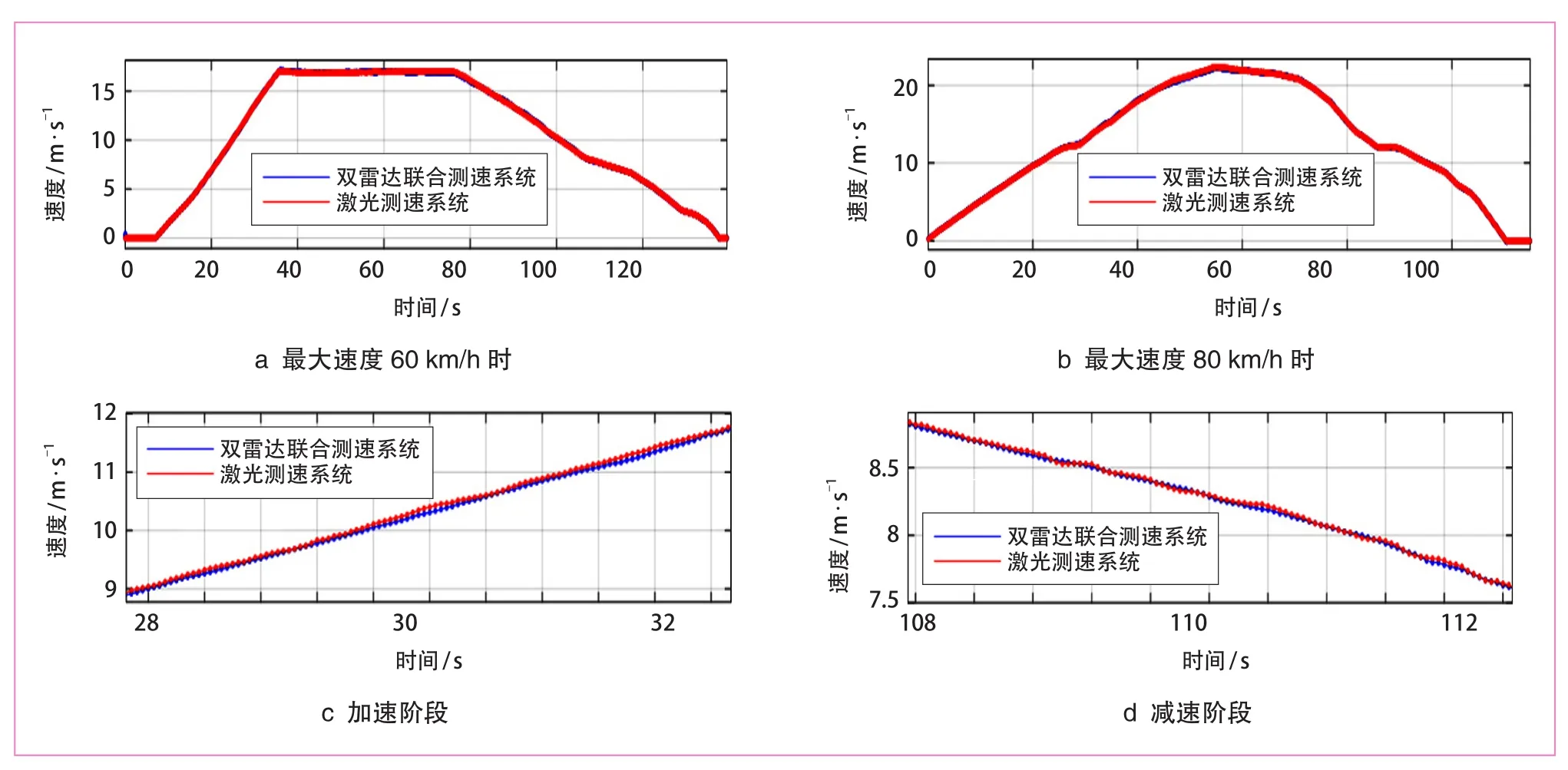
图7 双雷达联合测速系统与激光测速系统测量结果对比

6 结语

本文创新性地设计双雷达联合测速系统，并通过高性能高集成硬件电路实现系统的优化，为实现基于雷达探测技术的高精度、高可靠度列车测速提供了一种新的解决方案。