长短期记忆神经网络在多时次土壤水分动态预测中的应用①

范嘉智，谭诗琪，罗 宇，庄翔宇，周 伟，罗 曼

长短期记忆神经网络在多时次土壤水分动态预测中的应用①

范嘉智1,2，谭诗琪3，罗 宇1，庄翔宇4，周 伟1，罗 曼1

(1 中国气象局气象干部培训学院湖南分院，长沙 410125；2 气象防灾减灾湖南省重点实验室，长沙 410118；3 湖南省气象服务中心，长沙 410118；4 上海三澎机电有限公司，上海 200122)

基于长沙站2016—2019年10 cm深度土壤水分自动观测小时数据集，利用长短期记忆神经网络(LSTM)模型结合随机采样学习方法，开展了土壤水分多时次预测，结果表明：LSTM模型对6、12、24、48 h后的土壤体积含水量预测均方根误差(RMSE)分别为0.22%、0.28%、0.38%、0.54%，决定系数(2)分别为0.99、0.99、0.98、0.96，除6 h预测步长外，准确率均优于自回归整合滑动平均(ARIMA)模型，且误差稳定、无异常值出现，预测准确率远优于相关研究。该结果证实了基于LSTM模型精准预测土壤水分动态的可行性，为精准灌溉和干旱预警提供了计算机技术及手段支撑，为政府及科研部门水资源管理政策的制定提供了数据支持。

长短期记忆神经网络(LSTM)；土壤体积含水量；气象因子；多时次预测；精准灌溉

水分是地球上的重要资源，是“土壤-植被-大气”连续系统的关键纽带[1-2]。其中，土壤水分作为碳水循环中的关键变量，是植物水分的主要来源[3]。基于中国干旱缺水及水资源分布不均的国情，土壤水分的准确预测对于作物生长状况的判定、田间水分管理及施肥决策的制定有重要意义[4-5]。土壤水分含量及其动态变化受气象因子(降水[6]、蒸散、气温和太阳辐射等)、土壤特性[7]、地形[8]、地表覆盖等条件的影响[9]。对于固定观测站点的土壤水分，降水几乎是其唯一来源，气温、风和太阳辐射对蒸散(土壤水分消耗的主要方式)有着重要的影响[10]。相对于深层土壤，表层土壤更易受这些因子的影响，因而表现出更高的预测难度[11]。

目前主流的土壤水分预测方法大多使用经验模型[12]、线性回归模型[13-14]、时间序列模型[15]、神经网络模型[5,16-18]。经验模型较为简单、便于理解，但其参数具有较强的地域特征，模型的建立耗时长且低效；线性回归方法拟合非线性的土壤水分数据存在诸多限制，其准确度与预测的需求也有较大差距；时间序列模型因各地数据波动幅度差异预测准确性差异较大[19]，限制了模型的推广；神经网络模型经历多年发展，在多种气象、水文参数的预测上证实了其极强的拟合、预测能力[20-23]。因此，神经网络模型的合理构建有望更准确地预测土壤水分存在的非线性时空异质性[24]。

对土壤水分的准确探测与预测是精准灌溉的前提，有助于精细化农业生产。而由于受到多种因素的影响，土壤水分呈现出复杂的变化特征，有季节性的变化趋势，也有随机的特征变化，研究利用机器学习算法结合气象观测数据以提升土壤水分预测准确率，对于农业水资源管理和最终实现高产、优质农业有重要意义。

1 数据来源与研究方法

1.1 数据来源

研究数据为基于频域反射法自动观测10 cm深度的土壤水分数据，来源于湖南省长沙市黄花站自动土壤水分观测站。该站点位于28.21° N，113.2°E，海拔101.4 m，属于亚热带季风气候区，气候温和、降水充沛、雨热同期、四季分明，年平均气温17.2℃，年降水1 358 ~ 1 553 mm。本研究数据源自于全国综合气象信息共享平台(CIMISS)，选用2016年1月1日0时至2019年5月18日23时土壤体积含水量每小时数据，其中存在199条缺测数据及1条异常数据，占比0.68%，均采用前后均值进行插补。前期查阅文献及相关性分析确定了输入变量中的气象参数为：气压、气温、露点温度、相对湿度、水汽压、1 h降水量、最大风速、地面温度、5 cm地温、10 cm地温、15 cm地温、能见度，其均为同时间段的小时观测数据。将每小时对应的气象参数与土壤含水量整理为一个数据库，以此进行长短期记忆神经网络(LSTM)模型的训练和预测，并与自回归整合滑动平均(ARIMA)模型预测结果对比。

1.2 研究方法

1.2.1 LSTM模型介绍 人工神经网络(ANN)是一种模拟人脑运行方式而设计的计算模型，它通过类似于生物神经元的节点连接而成，不同节点间的连接被赋予不同权重，每个节点代表了一种特定函数，节点接收经过相应权重综合过的信息，经过激活函数计算输出信息至下一层节点。理论上来说，一个足够深度的人工神经网络可以逼近任意的函数，因此，神经网络作为一种可学习的函数结构，被广泛用于机器学习、数据拟合等领域，并取得了相当丰硕的成果[25]。

在如土壤水分时间序列这类时序数据的处理上，因每个时次的参数会受之前参数水平的影响，所以处理这些数据的神经网络需要具有记忆能力。20世纪八九十年代出现的循环神经网络(RNN)通过节点之间的连接，使其同时可以接收自身和其他节点的信息，形成具有环路的网络结构，能以很高的效率对序列的非线性特征进行学习[26]。长短期记忆网络(LSTM)[27-28]是循环神经网络的一种变体，它通过引入新的内部状态和门机制，有效解决了梯度爆炸和消失问题(图1)。作为目前最成功的循环神经网络模型，LSTM被成功应用在语音识别、机器翻译[29]、语音模型及文本生成等领域。

1.2.2 LSTM模型建立 LSTM模型的优势在于可以从多次的学习过程中挖掘数据间的联系，通过神经元之间的连接权重传递信息，并经过一次次的重复训练优化模型。本研究整理后的数据库共29 616条数据，包括气象参数和土壤体积含水量数据，为防止训练过程中的梯度爆炸，需要将参数进行归一化处理：

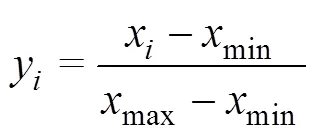
式中：x为土壤体积含水量观测数据集，y为归一化后的数据集，max、min分别为原始数据集中最大值和最小值，归一化后数据范围为[0, 1]。

选取数据库中约80% 数据作为训练数据，共23 692条数据，剩余数据作为测试集。因神经网络模型易出现过拟合现象，造成在训练数据上的拟合能力远好于测试集，所以在其中再选取约10% 的数据作为训练过程中的验证集，其余为训练集。若验证集的均方误差(MSE)在20轮训练内没有改进，则将MSE最小的那次训练作为最终模型，否则训练至设置的训练轮数。均方误差的计算如下：

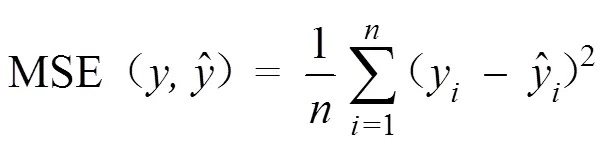
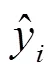
模型的训练需要提前设定参数，如神经网络层数、每层的神经元节点数、激活函数类型、训练轮数、优化器类型等。不适宜的模型参数会加大模型计算量、增大预测误差或降低模型泛化能力。经过在R语言中的多轮测试及优化，最终得出如下7层模型结构，见表1。模型输入数据为列表型三维结构数据，每一轮训练输入13个128×48矩阵数据组，其中13个数据组为包括土壤水分在内的13个输入因子，每一轮训练随机从训练集中抽取128条数据的前48 h至前1 h观测值组成输入数据列表，经本研究结构模型运行多轮后输出数据为128×4矩阵数据，对应128条数据的后6、12、24、48 h的土壤水分。为防止训练过程中的过拟合，在模型结构中添加的Dropput层是一种基于权重比例推断规则的正则化方法。模型激活函数选定为“linear”，优化器为“adam”，训练最大轮数定为500。

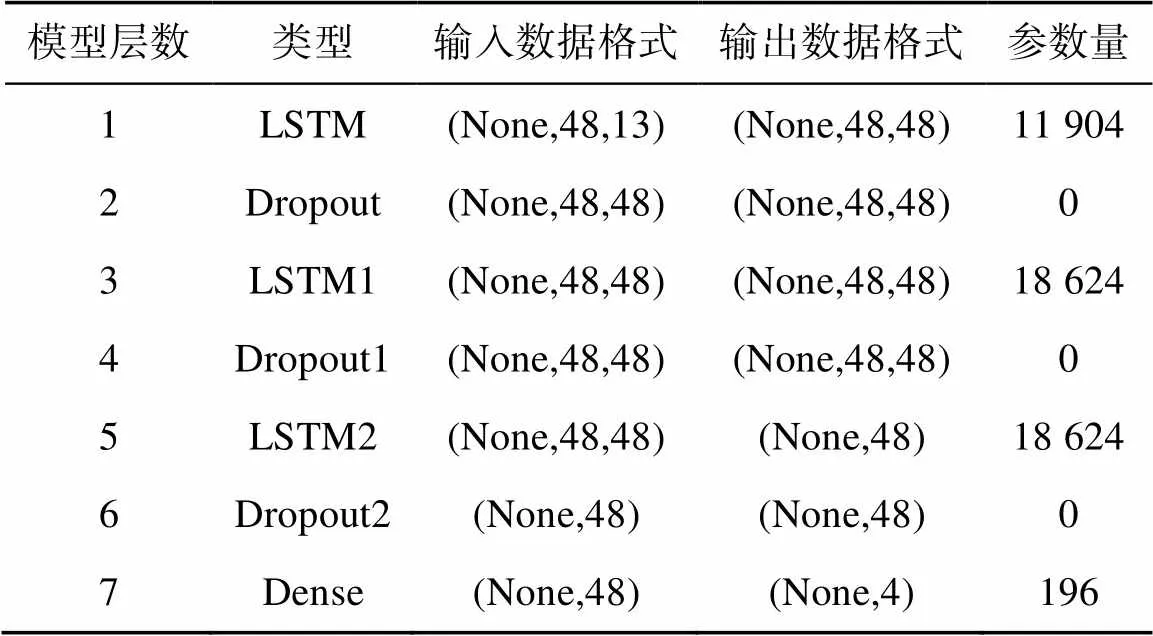
表1 土壤水分预测LSTM模型结构表

1.2.3 ARIMA模型建立 假定一个时间序列数据中部分是自回归，部分是滑动平均，可以得到一个较普遍的时间序列模型，如：

式中：e前为序列Y的阶自回归过程，其后为阶滑动平均过程，称{Y}为自回归滑动平均模型，阶数分别为和，简记为ARMA(,)。如果有一个时间序列{Q}的次差分：

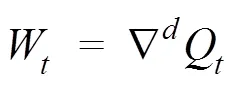
其是一个平稳的ARMA过程，则称{Q}为自回归整合滑动平均模型。如果W服从ARMA(,)模型，则称{ Q}是ARIMA(,,)过程。利用ARIMA模型预测土壤水分需要如下流程：①需要判断时间序列是否平稳，对于非平稳时间序列需要多次差分直到其平稳，差分次数记为；②计算序列的自相关函数和偏自相关函数，根据函数的截尾和拖尾状态决定和值；③建立 ARIMA(,,)模型，检验其是否具有统计学意义及判断残差序列是否为白噪声序列；④利用已通过检验的模型进行预测。为了避免参数不同造成的LSTM模型和ARIMA模型预测精度差异，ARIMA模型的输入序列也设置为前48 h的土壤水分数据，预测后6、12、24、48 h的土壤水分参数值，在循环算法下，每次引入新的时间序列均会重新建立ARIMA模型，并在99.5% 的置信水平下预测。

1.2.4 评价指标 对于LSTM模型预测精度的评价，利用训练后的模型对测试集数据6、12、24、48 h后的土壤水分进行预测，每一个测试集中的LSTM模型预测值均有对应时次的ARIMA模型预测值供对比。利用如下4种指标评价两种模型的预测准确性。

平均绝对误差(MAE)：

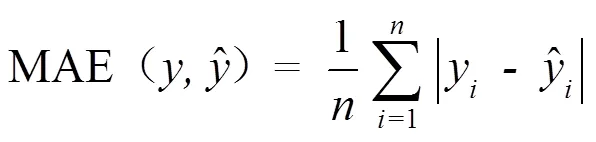
均方根误差(RMSE)：

相对误差值(RE)：

决定系数(2)：

1.2.5 数据分析软件 本研究模型建立、运行和计算及作图过程均在R语言(版本3.6.0)中完成。LSTM模型的建立基于keras深度学习框架(https://keras. rstudio.com)，ARIMA模型的建立利用了“forecast”包，作图利用了“ggplot2”包[30]。

2 结果

归一化之前的10 cm土壤水分时间序列如图2所示，虚线之前为训练集，虚线和实线之间为验证集，实线后为测试集。可以看出，该层土壤水分波动较大，但有一定的季节趋势，其中峰值出现在2017年7月1日下午4时，土壤体积含水量达40.5%，当时正值长沙遭遇超历史极值暴雨导致的严重洪涝灾害[31]。

图3为多轮训练下训练集和验证集的MSE结果，模型每一轮的训练及验证集对比时间共58 s，在第12轮训练时，针对归一化后的参数值，验证集上MSE为最小值0.003 28，并且此后20轮训练再无提升，故以第12轮训练的模型为最终模型。

使用LSTM模型在训练集和测试集上计算拟合值，并将其反归一化处理，使用ARIMA模型针对测试集中每个时次的土壤水分参数计算拟合值。利用评估参数对比LSTM模型训练集、LSTM模型测试集和ARIMA模型测试集中拟合值与真实值的差异性，评估参数如表2。LSTM模型拟合能力极强，训练集上随预测步长增加，误差增长较低。测试集上短预测步长下LSTM模型与ARIMA模型效果相似，随着预测步长的增加，ARIMA模型RMSE成倍增加，因此ARIMA模型预测的极端异常值较多，这也是其2明显偏低的原因。但LSTM模型测试集参数相对训练集有所升高，模型泛化能力仍有提升空间。

表2 LSTM与ARIMA模型拟合效果

图4中，在4个步长下，拟合值都能较好地捕捉到土壤水分的变化趋势，只是随着预测步长的增加，预测值与真实值间的误差略有增加，但仍处于可接受的范围内，其2也一直表现出0.9以上的高相关性，模拟效果较好。

图5和图6为6、12、24、48 h下的LSTM和ARIMA模型预测值与真实值的对比结果，可以看出，LSTM模型在较短的预测步长下，预测值与真实值基本一致，但随着步长的增加，对于土壤水分极端值的预测相对于中间值偏差较大(图5)。ARIMA模型在所有预测步长下都有极端异常值的出现，且异常值均为大值参数(图6)。

3 讨论

LSTM模型的一个重要优势就是能够通过学习挖掘和熔断参数间的联系，因此输入因子需要尽量全面且精简，且必须有足够的观测数据，否则会因欠拟合造成预测效果不佳[32]。降水是影响土壤水分最直接的要素，一般情况下土壤水分变化趋势与降水量变化趋势基本一致[33]，但由于降水的下渗过程，二者存在一定时间差[34]。总体而言，土壤的干湿季与气候的干湿季基本一致。降水对土壤水分的影响与降水量、强度、时长等诸多因素有关，一般大于10 mm的降水才能够使土壤水分含量发生改变[35-36]，这一阈值也与地表覆盖和土壤水分状况相关[10]。相关研究[3]证明，降水量与土壤水分间的相关关系因降水量级不同有所差异[37]，且会因随机性过强而产生干扰。湿度作为同样可以反映水分状况的指标，以及温度、风速、太阳辐射等作为影响蒸腾作用的指标，均有必要作为输入因子。气压和能见度与土壤水分的关系并不明朗，是否将其作为输入因子对预测结果影响极小，但基于LSTM模型的熔断机制，仍将其加入分析，通过LSTM模型的学习过程进行因子权重的设置。

作为一种高效的神经网络模型，LSTM模型鲜少被利用在土壤水分数据拟合及预测上。本研究对于土壤水分动态的成功预测证实了LSTM模型在复杂的土壤水分数据拟合上的能力，相对ARIMA模型其预测精度在短时间步长上相近，长时间步长上具有明显优势，且预测误差较稳定，没有极端值的出现。本研究基于LSTM模型的土壤水分预测效果与前人的研究相比有着较大的提升。冀荣华等[16]利用复数神经网络模型和误差反向传播神经网络模型对土壤墒情每小时观测数据进行预测，一步预测RMSE可达0.883、0.897 m3/m3，远低于本研究的准确率。Gill等[17]利用支持向量机法对4个和7个时次后的土壤水分进行预测，RMSE分别为4.05%、4.19%，其准确率低于本研究48个时次的预测准确率。聂红梅等[38]利用支持向量回归机基于气象、地形、土壤属性参数对土壤水分进行预测，表层土壤水分RMSE为7.521%，其精度低于本研究结果。李宁等[18]利用改进的自适应遗传神经网络算法对24 h后的土壤湿度进行预测，最优MAE可达到1.26%，远低于本研究的0.239%。

LSTM模型在多时次土壤水分预测上的成功应用证实了其在处理长时间序列数据时强大的拟合能力，本研究中所采用的7层模型结构为多次测试下的相对最优结构，但模型结构优化过程对于预测精度的提升较为有限。本研究中所构筑的输入集随机采样过程和训练过程中的检验、提前中止机制在机理上更符合时间序列数据的分析需求，也为LSTM模型的应用作出了辅助贡献。应用LSTM模型对多时次土壤水分的准确预测，为土壤水分的预测预报方式提供了技术指导，为农业生产水资源保障工作提供了数据支撑，可对现有预测方法准确率的提升提供指导方向，提高精准灌溉、干旱预警等工作的准确性。

4 结论

基于长沙自动土壤水分观测小时数据的研究证明，利用长短期记忆神经网络(LSTM)模型可以对土壤水分含量进行多时次预测，采用随机采样输入前48 h的气象观测数据和土壤水分含量数据，经过12轮学习和评估，所得模型预测后6、12、24、48 h土壤水分含量的RMSE分别为0.22%、0.28%、0.38%、0.54%，预测准确率远优于相关研究，但在优化模型提升泛化能力上仍有提升空间，研究结果可为精准灌溉和农业水资源管理提供数据支持。

[1] Schlesinger W H, Jasechko S. Transpiration in the global water cycle[J]. Agricultural and Forest Meteorology, 2014, 189/190:115–117.

[2] 张义, 谢永生, 郝明德. 黄土高原沟壑区塬面苹果园土壤水分特征分析[J]. 土壤, 2011, 43(2): 293–298.

[3] Cai Y, Zheng W G, Zhang X, et al. Research on soil moisture prediction model based on deep learning[J]. PLoS One, 2019, 14(4): e0214508.

[4] Chukalla A D, Krol M S, Hoekstra A Y. Green and blue water footprint reduction in irrigated agriculture: effect of irrigation techniques, irrigation strategies and mulching[J]. Hydrology and Earth System Sciences, 2015, 19(12): 4877–4891.

[5] 侯晓丽, 冯跃华, 吴光辉, 等. 基于人工神经网络土壤墒情动态预测模型应用研究[J]. 节水灌溉, 2016(7): 70–72, 76.

[6] 辛祥, 林青, 黄修东, 等. 大沽河下游农田土壤水分含量动态变化特征[J]. 土壤, 2019, 51(2): 390–398.

[7] Singh J, Milchunas D, Lauenroth W. Soil water dynamics and vegetation patterns in a semiarid grassland[J]. Plant ecology, 1998, 134(1): 77-89.

[8] 刘鑫, 毕华兴, 李笑吟, 等. 晋西黄土区基于地形因子的土壤水分分异规律研究[J]. 土壤学报, 2007, 44(3): 411–417.

[9] 王俊霞, 潘耀忠, 朱秀芳, 等. 土壤水分反演特征变量研究综述[J]. 土壤学报, 2019, 56(1): 23–35.

[10] 何其华, 何永华, 包维楷. 干旱半干旱区山地土壤水分动态变化[J]. 山地学报, 2003, 21(2): 149–156.

[11] 阿拉木萨, 周丽芳. 科尔沁沙地流动沙丘土壤水分空间变化特征分析[J]. 土壤, 2011, 43(3): 392–397.

[12] Jackson S H. Comparison of calculated and measured volumetric water content at four field sites[J]. Agricultural Water Management, 2003, 58(3):209–222.

[13] Hummel J W, Sudduth K A, Hollinger S E. Soil moisture and organic matter prediction of surface and subsurface soils using an NIR soil sensor[J]. Computers and Electronics in Agriculture, 2001, 32(2): 149–165.

[14] 舒素芳, 钱华峰, 邱小伟. 基于气象因子的金华市土壤墒情预测模型[J]. 中国农业气象, 2009, 30(2): 180–184.

[15] 刘洪斌, 武伟, 魏朝富, 等. 土壤水分预测神经网络模型和时间序列模型比较研究[J]. 农业工程学报, 2003, 19(4): 33–36.

[16] 冀荣华, 张舒蕾, 郑立华, 等. 基于多值神经元复数神经网络的土壤墒情预测[J]. 农业工程学报, 2017, 33(S1): 126–131.

[17] Gill M K, Asefa T, Kemblowski M W, et al. Soil moisture prediction using support vector machines[J]. Journal of the American Water Resources Association, 2006, 42(4): 1033–1046.

[18] 李宁, 张琪, 杨福兴, 等. 土壤墒情预测自适应遗传神经网络算法研究[J]. 计算机工程与应用, 2018, 54(1): 54–59, 69.

[19] 白冬妹, 郭满才, 郭忠升, 等. 时间序列自回归模型在土壤水分预测中的应用研究[J]. 中国水土保持, 2014(2): 42–45, 69.

[20] 石灵芝, 邓启红, 路婵, 等. 基于BP人工神经网络的大气颗粒物PM10质量浓度预测[J]. 中南大学学报(自然科学版), 2012, 43(5): 1969–1974.

[21] 崔东文. 多隐层BP神经网络模型在径流预测中的应用[J]. 水文, 2013, 33(1): 68–73.

[22] 黄小华, 李德源, 吕文阁, 等. 基于人工神经网络模型的风速预测[J]. 太阳能学报, 2011, 32(2): 193–197.

[23] Song X D, Zhang G L, Liu F, et al. Modeling spatio-temporal distribution of soil moisture by deep learning-based cellular automata model[J]. Journal of Arid Land, 2016, 8(5): 734–748.

[24] 刘凯, 高磊, 彭新华, 等. 半干旱区科尔沁沙地土壤水分时空特征研究[J]. 土壤, 2015, 47(4): 765–772.

[25] 周飞燕, 金林鹏, 董军. 卷积神经网络研究综述[J]. 计算机学报, 2017, 40(6): 1229–1251.

[26] Goodfellow I, Bengio Y, Courville A. Deep learning[M]. MIT press, 2016.

[27] Gers F A, Schmidhuber J, Cummins F. Learning to forget: continual prediction with LSTM[J]. Neural Computation, 2000, 12(10): 2451–2471.

[28] Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735–1780.

[29] Sutskever I, Vinyals O, Le Q V. Sequence to sequence learning with neural networks[EB/OL]. 2014: arXiv: 1409.3215[cs.CL]. https://arxiv.org/abs/1409.3215.

[30] Wickham H. ggplot2: elegant graphics for data analysis[M]. Springer, 2016.

[31] 蒋祺, 郑伯红. 城市雨洪调蓄空间对洪涝灾害影响研究——以长沙市2017年洪涝灾害为例[J]. 自然灾害学报, 2018, 27(3): 29–38.

[32] Prakash S, Sharma A, Sahu S S. Soil Moisture Prediction Using Machine Learning[C]. 2018 Second International Conference on Inventive Communication and Computa­tional Technologies (ICICCT), 2018: 1-6.

[33] 王孟本, 李洪建. 晋西北黄土区人工林土壤水分动态的定量研究[J]. 生态学报, 1995, 15(2): 178–184.

[34] 苏敏, 卢宗凡, 李够霞. 陕北丘陵沟壑区主要农作物水分利用与平衡[J]. 水土保持研究, 1996, 3(2): 36–45.

[35] 杨新民. 黄土高原灌木林地水分环境特性研究[J]. 干旱区研究, 2001, 18(1): 8–13.

[36] Coronato F R, Bertiller M B. Precipitation and landscape related effects on soil moisture in semi-arid rangelands of Patagonia[J]. Journal of Arid Environments, 1996, 34(1):1–9.

[37] 刘冰, 赵文智, 常学向, 等. 黑河流域荒漠区土壤水分对降水脉动响应[J]. 中国沙漠, 2011, 31(3): 716–722.

[38] 聂红梅, 杨联安, 李新尧, 等. 基于PCA-SVR的冬小麦土壤水分预测[J]. 土壤, 2018, 50(4): 812–818.

Application of Long/Short Term Memory Neural Network in Soil Moisture Multi-time Dynamic Prediction

FAN Jiazhi1,2, TAN Shiqi3, LUO Yu1, ZHUANG Xiangyu4, ZHOU Wei1, LUO Man1

(1 China Meteorological Administration Training Centre Hunan Branch, Changsha 410125, China; 2 Key Laboratory of Hunan Province for Meteorological Disaster Prevention and Mitigation, Changsha 410118, China; 3 Hunan Meteorological Service Center, Changsha 410118, China; 4 Senpro Mechanical & Electrical Co., Ltd, Shanghai 200122, China)

Based on the data set of hourly soil moisture automatic observation at 10 cm depths from 2016 to 2019 in Changsha Hydrometric Station, the neural network of Long/Short Term Memory (LSTM) combined with random sampling learning was used to carry out multi-time prediction of soil moisture. The results showed that RMSE of prediction in 6, 12, 24, 48 h was 0.22%, 0.28%, 0.38%, 0.54%, and coefficient of determination (2) was 0.99, 0.99, 0.98, 0.96, respectively. The prediction accuracy was better than Autoregressive Integrated Moving Average (ARIMA) model except the 6 h, the deviation was stable and no abnormal value appeared, the prediction accuracy was far better than relevant studies. The results prove that the feasibility of accurately predicting in soil moisture dynamics based on LSTM model, provide computer technology and means for accurate irrigation and drought warning, and data support for the formulation of water resource management policies by government and research institutions.

Long short-term memory; Soil volumetric moisture content; Meteorological factor; Multi-time prediction; Precise irrigation

S152.7

A

10.13758/j.cnki.tr.2021.01.028

范嘉智, 谭诗琪, 罗宇, 等. 长短期记忆神经网络在多时次土壤水分动态预测中的应用. 土壤, 2021, 53(1): 209–216.

中国气象局气象干部培训学院科研项目(内2018-015)和湖南省气象局短平快科研项目(XQKJ18B070)资助。

范嘉智(1992—)，男，安徽马鞍山人，硕士，工程师，主要从事农业气象研究。E-mail：fjz92419@hotmail.com