汽车涂装中虚拟重排序问题建模与求解

张 光 前， 何 晓 飞

(大连理工大学 经济管理学院，辽宁 大连 116024)

0 引 言

在汽车涂装时，当两个即将面漆的车身喷不同颜色时，喷头必须重新清洗.为避免喷枪清洗以及更换涂料等过程所引发的高昂切换成本[1]，涂装车间希望相同颜色的车身尽量排在一起.通常，从上一车间出来的车身序列无法自然地满足这一要求，需对进入的车身序列进行一定调整，尽量满足涂装车间对车身序列的要求.这就形成了汽车涂装中的重排序问题.在汽车生产中，不同车间对车身序列的要求也各不相同，因此重排序问题普遍存在于汽车生产过程中.

重排序模式有两种：带缓冲区的物理重排序(physical re-sequencing)和不带缓冲区的虚拟重排序(virtual re-sequencing)[2-3].物理重排序是通过设置缓冲区(buffer)来调整序列，重排序后的个体在序列中的位置会发生改变.在虚拟重排序中，个体在序列中的位置不变，发生变化的是分配到个体上的属性，以此实现序列重排.本文关注的是虚拟重排序问题.

Epping等[4]将需要涂装的车身序列看成是由一串有色字母组成的单词，通过置换相同的字母得到一个颜色变化次数最少的单词(paint shop problem for words，PPW)，并采用动态规划的方法求解了该问题.Epping等也证明涂装的虚拟重排序问题是NPC(NP-complete)问题.随后，一些学者对PPW问题进行了研究，如对PPW问题的一种特殊情况，即二元PPW问题，Bonsma等[5]探讨了该问题的下界；Andres等[6]得出了二元PPW问题颜色转换的期望值；Gorbenko等[7]提出了PPW(2，1)问题求解算法.Inman等[8]研究了按单装配(assemble to order，ATO)敏捷系统中位于涂装车间前和总装车间前的虚拟重排序问题，证明了在喷漆前后解耦和重新分配订单可以显著提高敏捷组装-订购系统的性能.Ribeiro等[9]综合考虑了喷涂和装配两个阶段的要求对车身进行排序，通过设立启发规则并结合tabu搜索，建立了车身排序问题的求解算法，并用数值试验进行了验证.Gavranovi[10]针对汽车涂装排序问题，建立了贪心算法和本地搜索相结合的求解算法，得到该颜色排序问题的近似解.黄刚等[11]介绍了实际生产中汽车涂装的虚拟重排序问题，给出了涂装问题颜色转换计数表达式，并用遗传算法(genetic algorithm)解决了车身排序问题，通过算例验证了算法的有效性.Sun等[3，12]提出了物理重排序和虚拟重排序相结合来解决汽车涂装问题思路，并针对不同情形提出了相应的启发式算法，数值试验表明了这些算法的性能和有效性.Estellon等[13]针对车身排序问题设计了两个搜索算法，并通过数值试验做了对比分析.Elahi等[14]针对通用汽车涂装车间传送系统，把离散事件仿真和决策优化相结合进行排序决策.

可见，目前虚拟重排序问题的研究焦点体现在建模和求解两个方面.由于虚拟重排序是NPC问题，导致现有关于虚拟重排序的模型通常较为复杂，有时甚至不能建立完整的数学模型；模型也无一例外地需要设计专门解法进行求解或采用智能算法求近似解.

本文针对汽车涂装涉及的虚拟重排序问题，建立相对易于得到解析解的数学模型，使研究成果更接近实际应用，同时也探讨关于问题规模增大所带来的求解困难的解决方向.

1 问题描述及符号设定

在涂装车间需要对白车身进行涂漆.白车身是指已完成焊装工序但尚未面漆的汽车车身.若进入涂装车间的白车身有5种类型，分别用字母A、B、C、D、E表示；需要喷涂的颜色有两种，分别用1和2表示.若进入涂装车间的白车身顺序为{A，C，D，A，B，C，C，E，D，B，A，E}.根据订单，这些白车身需要在涂装车间涂装的颜色分别为{2，1，2，1，1，2，2，2，2，2，1，1}，则进入涂装车间的车身序列为{A2，C1，D2，A1，B1，C2，C2，E2，D2，B2，A1，E1}.若直接按此序列进行喷涂，则喷头颜色需要变化5次.若对同型车身进行颜色互换，如把序列中车型同为A的两个车身颜色互换，则会使该序列的前两个车身都为颜色1.这种调整未实质性改变客户订单，但喷涂颜色转换次数可能会减少，从而达到总的颜色转换次数最少的要求.由于在此过程中没有用到缓冲区，此即车身涂装的虚拟重排序问题.

为了便于问题描述和建模，对本文所用符号说明如下：一般地，给定一个初始序列{N}，共有n个个体，每个个体同时拥有两种属性，其中第1种属性有p个属性值，第2种属性有q个属性值.对涂装问题把车型看作第1种属性，颜色看作第2种属性.

ej表示第j种颜色，是q维0-1向量，其第j个分量为1，其余分量为0.

Xi=(xi，1xi，2…xi，q)T，是一个q维0-1向量，表示给定序列{N}中第i个个体的颜色.

1表示每个分量都为1的q维向量.

nkj表示给定序列{N}中具有第k个第1种属性，第j个第2种属性的个体数量.

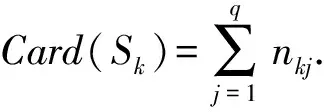
/·/是自定义的一种数学运算，表示对处于其中的向量的每个分量取绝对值.

Yi，i+1表示对应向量Xi、Xi+1的q维向量.

2 汽车涂装车间虚拟重排序的数学模型

涂装车间根据订单为汽车喷指定颜色的漆.由于喷头在转换颜色时会增加时间、物料、人工等方面的成本，涂装车间希望尽可能地减少喷枪颜色的转换次数.

进入涂装车间的车身序列是上游车间的出车间序列.对涂装车间来说，相当于给定了入车间序列.涂装车间需对入车间的车身序列进行调整以实现喷枪颜色转换次数最少的目标.在序列调整过程中，所关注的汽车属性为车身型号和车身颜色.通过互换相同车型的颜色，能做到订单无实质变化，但颜色序列会发生改变，从而实现车身序列的虚拟重排序.

根据虚拟重排序的特点，可以总结出涂装虚拟重排序的基本性质：(1)颜色唯一性.不论如何调整车身序列，每个车身最终只能有唯一的涂装方案.(2)统计结果不变性.重排序只改变了订单顺序，排序前后的两个序列中任一车型和颜色的车的数量保持不变.

用Xi表示第i辆车的涂装颜色.若其第j个分量为1，其余分量为0，则该辆车涂装第j种颜色.

根据颜色唯一性，对序列中的每个个体来说，最终被喷涂的颜色只能是一种，于是有

(1)

根据统计结果不变性，对于Xi、Sk和nkj来说，存在如下关系：

(2)

上式保证了颜色互换只发生在相同车型中，因此，任何特定车型和颜色的个体数目在序列优化前后保持不变.

此外，还需把颜色变化次数表示出来.在序列中相邻的两个个体，当用后一个个体的颜色向量减去前一个个体的颜色向量，并对得到颜色差值向量的每个分量取绝对值，则相邻两个个体(第i+1个个体和第i个个体)之间的颜色变化次数为

(3)

若相邻两个个体颜色不同，则式(3)的值为1，表示颜色发生了一次变化；当前后两个个体颜色相同，则式(3)的值为0，表示两个相邻个体颜色相同.

综合式(1)～(3)，建立汽车涂装虚拟重排序问题的数学模型：

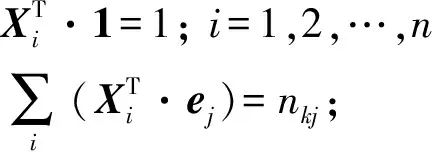
i∈Sk，j=1，2，…，q，k=1，2，…，p

Xi分量取值均为0-1变量

该模型为基本模型，其目标函数是总的喷枪颜色转换次数最少，对应式(3).约束分为3类，从上到下依次是：颜色唯一性约束，对应式(1)；统计结果不变性约束，对应式(2)；向量的每个分量均为0-1变量的约束.

3 对基本模型的转化与分析

基本模型建立了关于汽车涂装车间虚拟重排序问题的含义明确、关系清晰的数学模型.但目标函数含有本文定义的对向量分量取绝对值的运算，是非线性的，难以直接求解.根据0-1变量的特点，当把目标函数中的向量X用XTX来替代，此时，目标函数变为

(4)

注意到，Xi的分量都是0-1变量，因此式(4)表示颜色变化次数与原模型中的目标函数未发生实质性改变，但自定义的绝对值符号已经去掉.此时，基本模型变为目标函数是二次的、约束为线性的0-1整数规划.目前，常用求解软件不能直接求解一般意义上的0-1二次整数规划，需要对模型的目标函数进一步转化.

把式(4)中的通项(Xi+1-Xi)T·(Xi+1-Xi)展开：

(5)

(6)

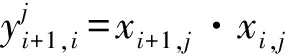
(7)

表1 0-1变量及其运算结果

从表1可见，前3列表示了xi和xj以及xi·xj的所有可能.第4列则是y对应xi·xj时的所有可能，此时y和xi·xj毫无关系.当加入约束条件(7)后，y的取值即y′(第5列)与xi·xj(第3列)完全一致.由于表1列出了xi·xj和y′所有可能的情形，在每一种情形下，y′和xi·xj都相等.因此，可用y′代替xi·xj.这类约束条件可称为变量替换约束.当引入这一类约束，目标函数就变为线性的，于是基本模型变为

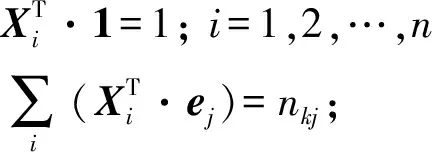
i∈Sk，j=1，2，…，q，k=1，2，…，p

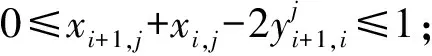
i=1，2，…，n-1，j=1，2，…，q

Xi分量取值均为0-1变量

z4是相邻个体颜色相同的数目，则实际发生颜色转换次数为(n-1)-z4，也就是z2(注意到z2=z3)，故有z2+z4=n-1.表明一个给定序列颜色相同和不同的相邻个体总数是固定的，总是序列个体数减1.

对于给定序列{N}，所建立的0-1线性整数规划(模型1)共有n个颜色唯一性约束；pq个统计结果不变性约束；2(n-1)q个变量替换约束；2(n-1)q个0-1变量约束，也就是0-1变量的个数.出现在目标函数中的变量有(n-1)q个.

4 模型应用

4.1 模型1的应用示例

为了从不同侧面清楚地展示模型1的建立和求解，模型用向量的分量表示.以在问题描述中给出的例子为例，对给定的序列{A2，C1，D2，A1，B1，C2，C2，E2，D2，B2，A1，E1}，要求对该序列进行虚拟重排序以实现颜色转换次数最少.根据给定的序列有n=12，p=5，q=2.此时，原始序列关于车型和颜色两种属性的个体统计结果如表2.

从表2可见，对SA，有SA=nA1+nA2=2+1=3.对给定序列，当i∈SA时，有i=1，4，11(见给定序列).

表2 原始序列中车型和颜色的个体数目统计结果

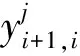
模型：

s.t.xi，1+xi，2=1；i=1，2，…，12

x1，j+x4，j+x11，j=nAj；i∈SA，j=1，2

x5，j+x10，j=nBj；i∈SB，j=1，2

x2，j+x6，j+x7，j=nCj；i∈SC，j=1，2

x3，j+x9，j=nDj；i∈SD，j=1，2

x8，j+x12，j=nEj；i∈SE，j=1，2

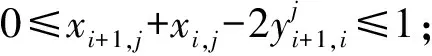
i=1，2，…，11，j=1，2

所有变量均为0-1变量.该模型有n+pq+2(n-1)q=12+5×2+2×11×2=66个约束条件(不含关于变量是0-1整数这一约束)，有(n-1)q+nq=(12-1)×2+12×2=46个变量.

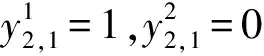
根据xi，j的值(也可以根据yi+1，i值)得到优化后的颜色排序为{1，1，2，2，2，2，2，2，2，1，1，1}，重排序后的序列为{A1，C1，D2，A2，B2，C2，C2，E2，D2，B1，A1，E1}.可以看出，在第2、3个个体以及第9、10个个体间各发生了一次颜色变化，共发生了2次颜色变化.若初始序列不进行虚拟重排序，则需要5次颜色变化.

4.2 考虑最大喷涂量限制的模型扩展

在实际生产过程中，喷枪在连续喷涂一定数量的车体后，也需要进行及时的清洗维护，以免出现气孔和通道堵塞等影响车身喷涂质量问题.且当检查人员面对过长的相同颜色汽车序列时，其检查故障的能力会降低[15].因此，汽车涂装时一般会设置一个最大喷涂量，即连续喷涂相同颜色的车辆不能超过最大喷涂量.

若允许的最大喷涂量为m，则在任意连续的m+1个喷涂车辆中，至少存在一组两个位置相邻的车辆是不同颜色，即：

(8)

式(8)为最大喷涂量约束.该约束条件是非线性的，其非线性项与基本模型目标函数的非线性项完全相同，故可以采用同样的处理方法，使之变为线性约束.此时，会在约束条件中增加n-m个最大喷涂量约束.

若考虑最大喷涂量限制(设m=5)，则在模型1基础上增加该类约束即可.使用Matlab软件对该问题进行求解，结果汇总如表3.

表3 虚拟重排序的解

5 结 语

本文探讨了关于汽车涂装虚拟重排序问题的建模与求解.在对虚拟重排序特点进行提炼的基础上，把颜色做了编码，建立了关于涂装虚拟重排序的0-1二次整数规划模型，并提出了把模型中二次表达式转化为线性表达式的方法，从而最终建立起关于涂装虚拟重排序问题的0-1线性整数规划模型.由于属性是颜色还是其他对所建立的模型并无实质性影响，故所建模型可用于任何虚拟重排序问题.

所建立的0-1线性整数模型的变量和约束条件的个数大致在max{np，nq，pq}数量级，即模型本身规模和问题的参数(n，p，q)之间大体是二次方关系.尽管0-1线性整数规划目前尚无一般的多项式时间算法，但已经有很多求解软件，如Matlab、CPLEX、LINGO等，都可以直接求解这类问题，无须设计专门的求解算法就能求得精确解.这是本研究与以往虚拟重排序问题研究最大的不同.

此外，除了借助于计算机技术、优化方法等，寻找问题本身的特点应该是解决虚拟重排序问题的努力方向之一.因为从更长的时间跨度看，序列的规模会很大，但属性种类和取值有限，这就意味着这类排序问题不但会存在具有相同序列的片段，而且极可能存在如“再生长点”类似的性质，即对于给定序列，其中存在一个或多个节点.这些节点有如下的性质：当按照这些节点把序列分为小的序列时，对每个小序列进行虚拟重排序，这些小序列虚拟重排序的结果和把整个序列直接进行虚拟重排序的结果一致.此时，问题的规模就会大大降低，计算复杂性也随之大幅下降.“再生长点”方面的研究，也许是解决虚拟重排序问题一个值得尝试的思路.