基于欧拉-欧拉方法的细长管道内磨粒流加工数值模拟研究

刘 宵， 尹 洪 超， 穆 林

(大连理工大学 能源与动力学院 辽宁省复杂能源转化和高效利用重点实验室，辽宁 大连 116024)

0 引 言

固液两相流体的流动和相互作用在工业生产过程中非常普遍.如石油、泥浆、雨水在管道中的输运过程，流体中夹杂的固体颗粒会在管道中沉积、磨削壁面[1]；在传热传质领域，在流体中加入固体颗粒，会提高流体的对流换热系数，使传热过程得到强化[2].20世纪60年代，美国宇航局为去除航天用液压阀体等装置的内部毛刺，提出一种利用两相流抛光零部件表面的加工工艺，即磨粒流加工工艺(abrasive flow machining，AFM)[3].

近年来，AFM工艺不断完善，表现出抛光效率高、适应性强、对工件损伤低、表面压应力提高等优势，并得到了广泛关注和应用[3].国外研究方面，Williams等[4]以AFM的加工方式对密封板的铝-钢接触部位进行抛光加工，极大提升了金属板密封、防泄漏的效果.Davies等[5]研究了不同黏度的流体与不同粒径的颗粒对AFM加工的影响.Petri等[6]考虑了影响磨粒流加工的诸多参数，设计出适合各种流体和被加工材料的AFM预测系统.国内研究方面，周迪锋等[7]以CFD-DEM耦合模型研究了磨粒撞击次数和撞击速度对于抛光效果的影响.李琛[8]以可实现k-ε湍流模型和软性磨料的方法研究了磨粒流加工过程中速度、压力、湍流动能、湍流耗散率等诸多流体参数的分布特征.高航等[9]指出，磨粒粒度特性以及不同黏度的流体流动特性对AFM加工过程具有显著影响，仍需进行深入研究.

另一方面，基于加工机理的仿真建模和数值分析过程可以分为流体流动和颗粒运动两个方面.其中，以流体流动为研究重点的主要目的是为了得到整个流场内的压力、速度、湍流强度等分布情况，这是影响磨粒流加工特性的宏观因素，可以对加工后的结果进行定性预测.此类研究大多选择了基于拉格朗日方法的Mixture模型[10]或VOF模型[11]，适用于复杂曲面加工、磨粒表面的追踪以及湍流脉动的研究[12].而以颗粒运动为研究重点，则可以更好地得到局部磨削程度的规律，以及颗粒对壁面磨削量的预测.此类研究大多采用了DPM(discrete phase model)或DEM(discrete element method)，分别适合模拟颗粒轨迹追踪和颗粒之间的相互作用规律.本文的研究对象为某船用高压氧输送管道，该管道是一种狭长的异形管道，适合从流体的角度来研究AFM加工效果.相关领域的学者们大多采用欧拉-拉格朗日的方法进行研究[13]，先求解流体场，再将部分流体参数代入求解固体颗粒的运动，这样可能会导致固体颗粒的运动参数不准确，因此本文以欧拉-欧拉方法为原理构建仿真计算模型，该方法采用两套方程分别对流体和固体进行求解，并以相对速度、作用力等进行耦合，避免流、固参数的混淆.同时，考虑AFM加工过程中可能的传热及传质特性对加工过程的影响，重点研究颗粒粒径、磨料入口温度、磨料流体物性参数及流动特性等对壁面磨削特性的影响规律.

1 数学模型

数学计算模型以CFD理论为基础，包括两相流方程、湍流方程、能量方程.在固液两相流动的耦合计算方面，采用基于欧拉-欧拉原理的求解方法，将固体相(solid phase)视为流体，与液相(liquid phase)相互渗透，考虑固体颗粒相之间以及固液两相之间的相互作用.对固体、流体分别采用独立的方程进行求解，其连续方程和动量方程如下：

(1)

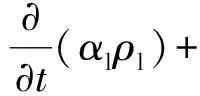
(2)

(3)

(4)

式中：α为体积分数，ρ为密度，t为时间，v为速度，m为传递的质量，S为源项，p为压力，τ为应力应变张量，g为重力加速度，F为外部体积力，下标s、l分别表示固相和液相，下标sl和ls分别表示从固相到液相和从液相到固相传递(或作用)关系，lift表示上升，vm表示虚质量.两相间的相互作用力Rsl和Rls分别见式(5)和(6)：

Rsl=Ksl(vs-vl)

(5)

Rls=Kls(vl-vs)

(6)

式中：Ksl和Kls为两相之间的动量交换系数，与摩擦、黏滞等效应有关.

式(3)和(4)中，Flift为升力，Fvm为虚质量力，表示固相相对于液相相对运动时，固体颗粒受到的惯性作用，计算公式分别为

Flift=-0.5αsρl(vl-vs)×(×vq)

(7)

(8)

液相和固相方程之间的平衡关系通过Rsl、Rls、Flift、Fvm耦合进行计算.

湍流方程采用基于雷诺平均的Navier-Stokes方程(RANS)，湍流动能方程和耗散率方程如下：

(9)

(10)

式中：k为湍流动能；vi为速度；μ为流体的动力黏度；μt为湍动黏度系数；Gk为由速度梯度产生的湍流动能；ε为湍流耗散率；σk为湍流动能普朗特数，取1；σε为湍流耗散普朗特数，取1.3；C1、C2为经验常数，分别取1.44和1.92；ν为流体运动黏度.由于本文研究的流体介质具有不同黏度特性，为了更精确求解湍流黏度，式(9)和式(10)中的μt不宜取为常数，而采用下式计算：

(11)

(12)

固相和液相流动过程的能量传递按下式计算：

式中：h为比焓，u为热力学能，q为热通量，Q为热交换量.

2 物理模型

2.1 几何模型

本文以某船用高压氧输送管道为研究对象，构建了直管、三通管和U形管3种管型结构的物理模型，其几何参数见图1，管道外径和内径均取R=18 mm和r=9 mm，L为从流道入口到出口的长度，取L=6 m.管子材料为铜镍合金，物性参数见表1.

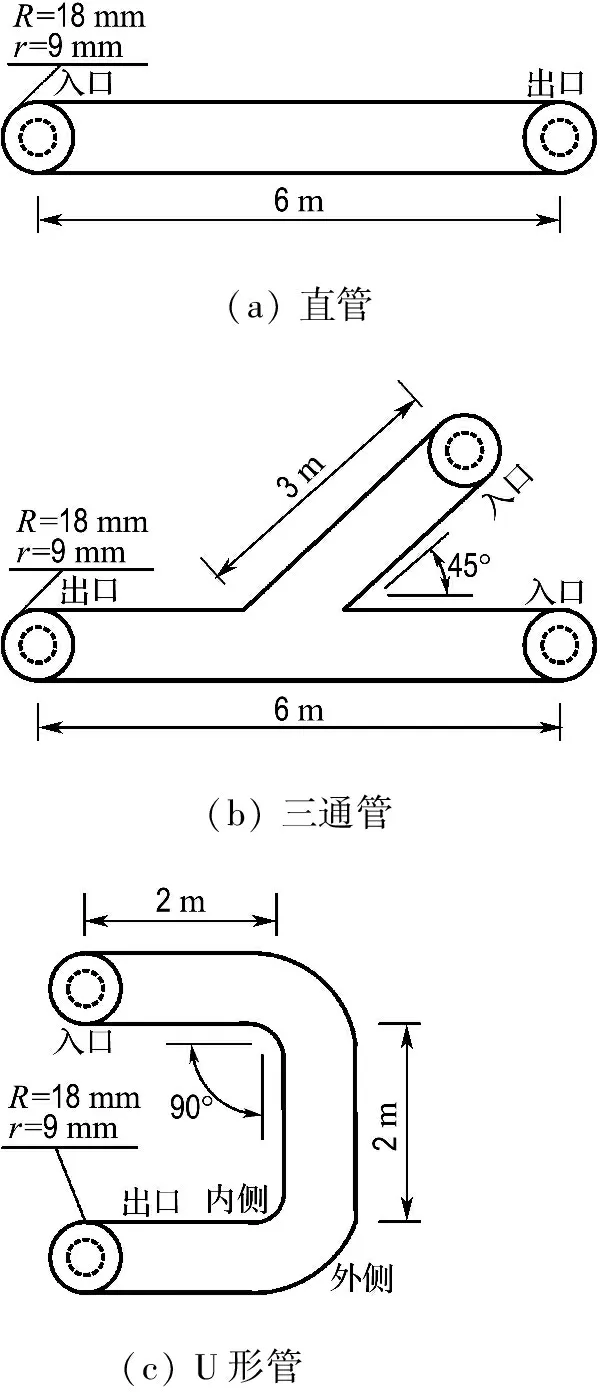
图1 物理模型

表1 管子物性参数

2.2 模拟设置

以ANASYS18.2系列软件为模拟工具，首先使用ICEM-CFD进行几何模型的建立和网格划分，区分流体计算域及固体计算域，由于模型尺寸较长，为提升计算速度，在长直段的网格划分稀疏，在接头部及弯部的网格划分较为密集.3种管型的网格数量在220×104～260×104.

选择Fluent软件为仿真计算工具，开启Realizablek-ε湍流模型、能量方程、多相流模型.根据流速、颗粒浓度的相关研究可知[8，13]，速度会对AFM加工效果有较大影响，而颗粒浓度的影响较小.为实现较好的磨削效果同时避免颗粒沉积现象的出现，通常选取较高的入口速度以及较高的磨粒浓度[14].因此入口速度设置为30 m·s-1，液相设置为水.固相设置为SiC颗粒，体积分数为10%，为研究不同颗粒粒径对AFM加工过程的影响，选取了3种颗粒直径d=10，50，100 μm分别进行模拟.磨粒流的初始温度分别设置为293、323、363 K.出口边界条件为流动出口.内壁面的表面粗糙度取50 μm，摩擦因数0.5；外壁面设置为对流换热表面，对流换热系数为20 W·m-2·K-1，环境温度T0为293 K.

2.3 模型验证

为确保仿真计算结果合理，分别进行网格无关性验证和数值模型可靠性验证.对直管几何模型进行网格加密处理后，得到的压强分布与未加密时基本吻合，见图2，表明本文划分的网格数量能够满足计算精度要求.此外，将李俊烨等[15]对喷嘴小孔的磨粒流加工实验结果与本文方法所建立的喷嘴小孔模型仿真计算结果进行对比，见图3.结果表明，计算得到的速度分布与实验结果之间的最大偏差为9.8%，可以认为本文选择的模型是准确的.

图2 直管压力曲线

图3 不同模型速度曲线的对比

3 结果分析

3.1 粒径对抛光过程的影响

Preston方程[16]是使用较为广泛的定量评价材料磨削加工的经验公式.式中的压力、速度、时间3个主要变量也是磨粒流加工过程中的重要变量，通过流体参数即可直接描述管壁的磨削效果.其表达式为

(15)

式中：Δz为材料去除量，kP为Preston系数，定义λ=vp，并通过λ的大小反映磨削程度的多少.

不同粒径的颗粒与壁面发生碰撞时，会有不同的碰撞形态.当颗粒粒径大于壁面的表面粗糙度时，其碰撞形式为弹性碰撞；颗粒的粒径小于壁面的表面粗糙度时，颗粒可以进入相邻凸起之间的缝隙中，除弹性碰撞外，还会产生犁、削的效果[17].除此之外，大颗粒具有较大的动能，单个颗粒与壁面碰撞时的磨削量更多，λ更大.因此，大粒径的颗粒具有更好的磨削效果，但是在磨削至一定程度后，弹性碰撞的作用效果不再明显，需更换小粒径的颗粒进行犁、削，才会使壁面粗糙度进一步降低.3种管型λ分布见图4.粒径d=10 μm时，U形管的λ曲线波动较为明显，这主要是由于U形管的几何模型特点，流道分成内侧(曲率较小一侧)和外侧(曲率较大一侧)，见图1(c).流体在转弯处的内、外侧会产生较大的速度、压力差，并会对接下来的流动过程产生扰动.此外，小粒径颗粒对壁面施加的弹性碰撞和犁、削综合作用，导致局部压力、速度波动较大，进而导致局部的λ波动较大.而直管与三通管中的流体均没有受到因流道转弯产生的内、外侧扰动，因此局部λ变化较为稳定.出口压力设置为0，入口压力根据过程的压降进行耦合计算，因此总体上λ呈下降趋势，但在入口处，流体进入管内后，其流动会向充分发展段过渡，使得近壁区的速度增加，进而导致λ在入口位置先呈现出增加的趋势.

图4 不同管型λ曲线

相关研究[8，10]侧重于流体和固体颗粒对壁面的磨削综合作用效果，因此通常将流体的速度和压力假设为固体颗粒的速度和压力.本文采用欧拉-欧拉模型进行模拟，对流体和固体颗粒分别分析了λ的变化趋势.总体上看，流体与固体颗粒的差异并不明显.但是在U形管的局部，以及三通管的汇合处，λ差异较为明显.这是因为相比于流体，固体颗粒具有更大的惯性，同时流体是连续的，固体颗粒是不连续的，因此固体颗粒运动状态的变化具有一定的滞后性.在稳定的流段中，流体与固体颗粒可以保持相同的运动状态，但在不稳定的流段中，固体颗粒与流体在经历转向、碰撞等过程后，会产生相对的滑移速度，使得局部的运动状态产生明显的差异.此外，粒径的大小也会影响流体和固体颗粒对壁面的作用差异.粒径越小，其惯性越小，宏观运动的形式越接近流体，因此流体和固体颗粒的λ差异越小.根据3种管型管内流动的特性可以推测，在更复杂模型的AFM加工过程中，流体与磨粒的流动差异更加明显，不能以流体的运动参数代替固体的运动参数.

3.2 入口温度对抛光过程的影响

U形管的流道既有长直部分，又有局部突变部分，而对温度分布的研究与管型关系不大，因此选择U形管为研究对象.为避免流体介质出现凝固、沸腾等相变现象，同时又要突出温度的差异性影响，液相流体水分别选取3个不同的初始温度Tw=293，323，363 K，表2为3种温度下水的物理性质.

表2 不同温度下水的物性参数

由图5可看出，温度Tw=293 K时的加工效果最好，这主要是两方面原因导致的.从液相来看，温度较低时，流体的密度较高，对管壁可以产生更大的挤压力；同时，该温度下流体表面张力较大，对于固体颗粒有更强的包裹性，在近壁区会对壁面产生更大的弹性力.从固体颗粒来看，金属材料以及SiC颗粒在低温时，密度也会增大，从而单个颗粒具有的动能更大；此外，低温时材料的韧性较低而脆性较大，SiC颗粒碰撞壁面的粗糙部位时，产生的冲击力更易使粗糙部位被磨削掉.

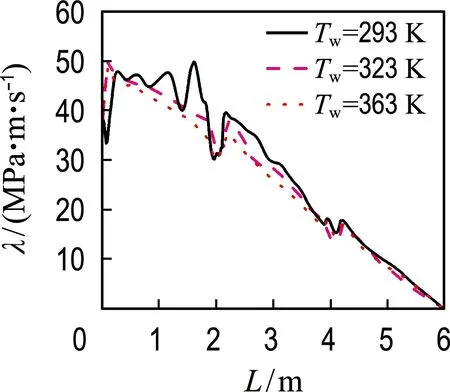
图5 不同温度下的λ曲线

AFM加工过程中，流体、固体颗粒与管壁摩擦，会有大量热量产生.本文模拟加工时间1 h，在外界环境温度T0=293 K的情况下，Tw与T0的温差ΔT越小，则磨削过程中的热积聚量越多.在管子不同L处的温度分布基本均匀，只在进出口部位有所差异，因此选取了L=0和L=3 m两个位置的截面进行分析.图6中，T表示截面各处的温度.随着加工时间的延长，管壁温度会逐渐升高，如前文所述，温度的升高会对加工产生不利影响.因此在加工过程中，对管壁适当进行冷却，或采取间断加工的方式，有利于实现更好的加工效果.

图6 截面温度云图

3.3 流体介质对抛光过程的影响

本节同样选取U形管为研究对象，对不同流体介质对抛光过程影响进行研究，见图7，流体介质分别为水和酒精时，λ具有一定的差异，为进一步研究这种差异产生的原因，本文选择了流体的密度和动力黏度作为研究对象.静压和动压计算公式中都包含密度变量，因此密度变化会对压强分布造成影响.动力黏度表示流体中发生相对运动所需要的力的大小，从而会对流速、压力产生影响.为此，补充两种假想流体进行模拟.流体A的动力黏度与酒精相同，其他物理性质与水相同；流体B的密度与酒精相同，其他物理性质与水相同，4种流体的主要物性参数见表3.

表3 不同流体物性

图7 不同流体的λ曲线图

结果表明，流体的密度越大，对管壁的挤压程度就越大，从而壁面受到的压力越大.因此密度主要是通过影响压强大小进而影响λ的大小.流体的动力黏度反映了流体与管壁产生相对运动时的摩擦力大小.流体的动力黏度大，宏观表现为黏滞性高、流动所受的阻力大，损失的动能用于磨削壁面，即壁面受到了更大的切削力作用，因此当流体的动力黏度升高时，磨削效果会提升.综合密度与动力黏度影响因素，流体A的动力黏度虽然小于流体B，但密度较比于流体B的更大，因为在本文模拟工况中密度起主导作用，流体A的λ更高.根据结果可以预测到，选择密度大、动力黏度高的流体作为介质进行AFM加工，可以获得较好的加工效果.

4 结 论

(1)磨粒粒径对AFM加工效果有显著影响.磨粒粒径大于壁面表面粗糙度时，单位时间内的材料磨削量较大；磨粒粒径小于壁面表面粗糙度时，U形管道流动的局部λ波动较大.磨粒粒径增大使得流体相和固体相在流道的突变部位对管壁的作用差异明显增强.

(2)分析了入口温度对AFM加工的影响规律，得到了不同入口温度下的AFM加工过程热量积聚分布云图，结果表明降低加工温度、维持管壁恒温更有利于加工过程.

(3)研究了不同流体介质对AFM加工效果的影响.以流体的密度和动力黏度为变量，对水、酒精以及两种假想流体进行模拟，得到了以高密度、高动力黏度的流体作为磨粒流介质更有利于AFM的结论.