考虑岩石细观结构的PFC模型及一种新的标定流程
武鑫星, 黄 兴, 王俊杰, 张全太
(1.中铁十二局集团第二工程有限公司,太原 030032;2.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室,武汉 430071;3.武汉大学土木建筑工程学院,武汉 430072)
颗粒流程序(Particle Flow Code,PFC)是显式离散元方法(DEMS)的一个分支[1],能够处理复杂的大变形问题,简单准确地观察破裂和破碎过程[2],因此广泛应用于岩土工程领域的研究[3-5]. 花岗岩是隧道、水利水电等岩土工程中一种常见的岩体,晶体结构明显,具有高强度比(单轴抗压强度与抗拉强度之比,即UCS/TS)、脆性大等特点. 但目前常用的标准结合粒子模型(Bonded Particle Model,BPM)[6]存在模拟材料的强度比远小于真实材料强度比的问题[7]. 研究表明,BPM 采用独立的接触圆盘模拟真实材料的细观结构,颗粒容易旋转;工程中的岩土材料由不规则晶体颗粒胶结而成,晶粒不易旋转,二者的差异是造成模拟材料与工程中的岩土材料强度比差异较大的主要原因[7].
针对BPM存在的问题,Cundall和Potyondy[6]提出了簇平行黏结模型. 相较于BPM,簇平行黏结模型将一定数量的相邻圆盘集合为簇,形成具有不规则边界的晶体结构,晶体内部和晶体之间具有不同的黏结强度,以此模拟脆性花岗岩中不规则晶体的强咬合作用,实现校准模型的宏观响应,如图1所示. 簇平行黏结模型包含两类[8](见图2),区别在于a类簇平行黏结模型簇内单个圆盘旋转被抑制,无法发生穿晶断裂;b类簇平行黏结模型簇内圆盘可以发生一定的旋转,可以发生穿晶断裂,因此可以称之为脆性簇平行黏结模型.Cho 等[9]对脆性合成材料进行了实验室直接剪切试验,并采用簇平行黏结模型模拟剪切过程,数值模拟与直接剪切试验结果基本一致;Li等[10]同时采用BPM、a类簇平行黏结模型和脆性簇平行黏结模型,对TBM楔形压头的破碎机理和破坏过程进行了数值模拟,结果表明穿晶断裂的脆性簇平行黏结模型校准结果和模拟结果均与室内试验结果最为一致;花岗岩的室内力学性能测试表明,由于晶体形状和晶体接触角度的原因,同时存在沿晶体边界断裂和穿晶断裂两种破坏模式(见图3). 可见,脆性簇平行黏结模型用于研究脆性岩体的力学和破坏行为具有更好的效果.

图1 花岗岩及簇平行黏结模型结构Fig.1 Structure of parallel bonding model of granite and clusters
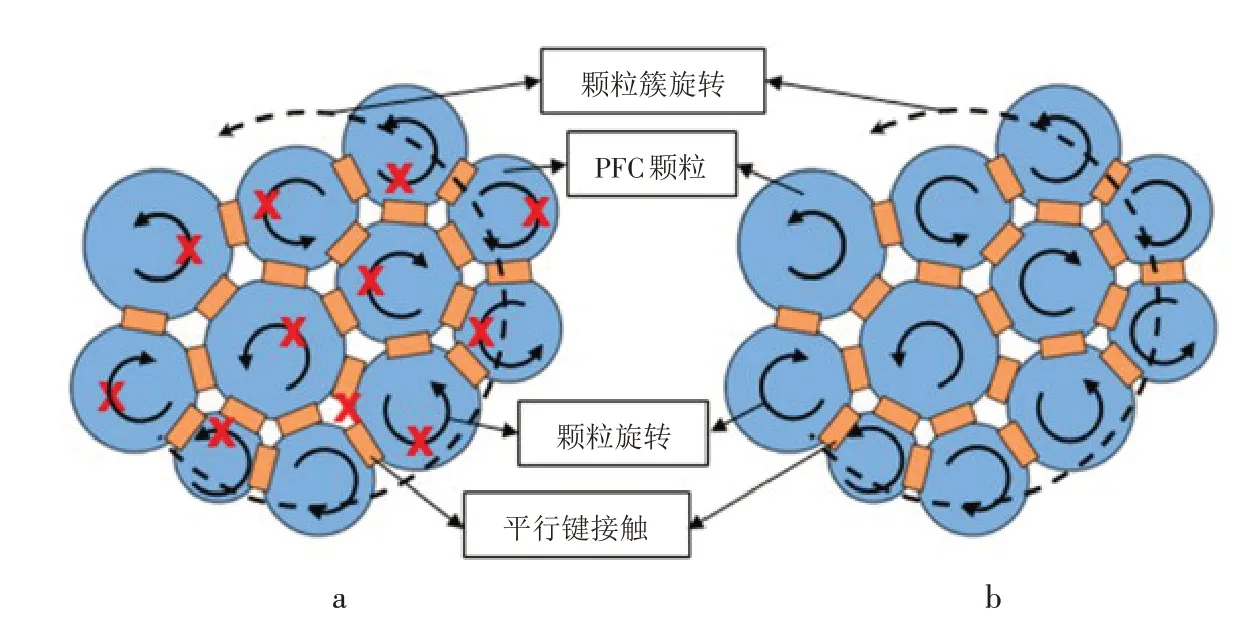
图2 两种簇平行黏结模型Fig.2 Two cluster parallel bonding models

图3 室内花岗岩巴西劈裂试验破坏模式Fig.3 Failure mode of indoor granite Brazilian split test
PFC模型参数的标定通常根据室内单轴压缩和巴西劈裂试验测得的工程中岩土材料的宏观参数确定[8],对其应用于岩土工程领域力学、破坏行为的研究有决定性影响,且具有耗时、不确定性较强等特点. 不少研究人员对模型参数的标定进行了研究[11-16],但目前对脆性簇平行黏结模型的标定过程鲜有研究. 因此,本文首先研究脆性簇平行黏结模型中主要微观参数对宏观性质的影响,并据此提出一套标定流程;然后基于提出的标定流程对某高铁隧道花岗岩进行标定,同时采用声发射监测该花岗岩室内单轴压缩试验的破坏过程与模拟过程对比,验证该模型模拟过程的可靠性和本文提出的标定流程的有效性.
1 脆性簇平行黏结模型的标定

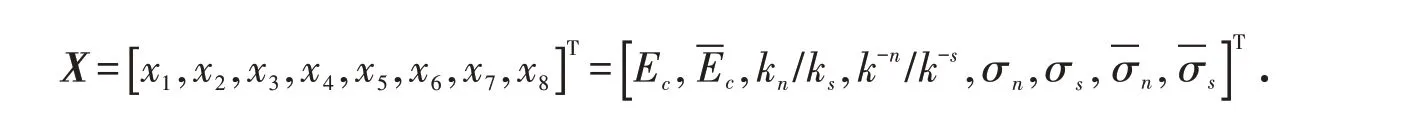
每一个宏观参数都是因变量,受微观参数变化的影响[12,17],可以用函数模型表示,即微观参数对宏观参数E、ν、UCS、TS的影响模型分别为:

由式(1)、式(2)、式(3)和式(4)可定义多目标优化模型的总标定误差模型如下:
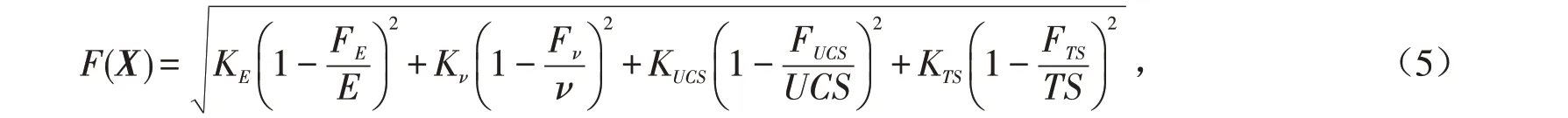
式中:KE、Kν、KUCS、KTS分别为E、ν、UCS、TS的权重系数,且KE+Kν+KUCS+KTS=1.0 .
标定的过程就是调整微观参数使F(X)不断减小,通过研究各微观参数的变化对宏观参数影响的趋势和大小,提出一种流程化的标定方法,优化脆性簇平行黏结模型标定过程,可以减少标定耗时.
减少自由微观参数可以提高标定速度,因此做以下假设[6,12,17-18]:①颗粒密度ρ=2630 kg/m3;②颗粒刚度比kn/ks与平行黏结刚度比-kn/-ks相同,即kn/ks=-kn/-ks;③颗粒接触模量与平行黏结模量相同,Ec=-Ec;④颗粒半径放大系数为1. 此外模型中最小颗粒半径Rmin=0.2 mm,颗粒半径比Rmax/Rmin=1.66,簇中颗粒数为20,加载速度为0.04 m/s. 为降低随机数不同对模拟结果的影响,对每一种微观参数组合使用三个不同随机数产生三个不同的模型,取三个模型宏观参数的平均值作为该微观参数组合模型对应的宏观参数.
1.1 kn/ks 和-kn/-ks 对宏观参数的影响


UCS和TS的变化没有明显的规律,且kn/ks的变化对四个宏观参数的影响都较大.
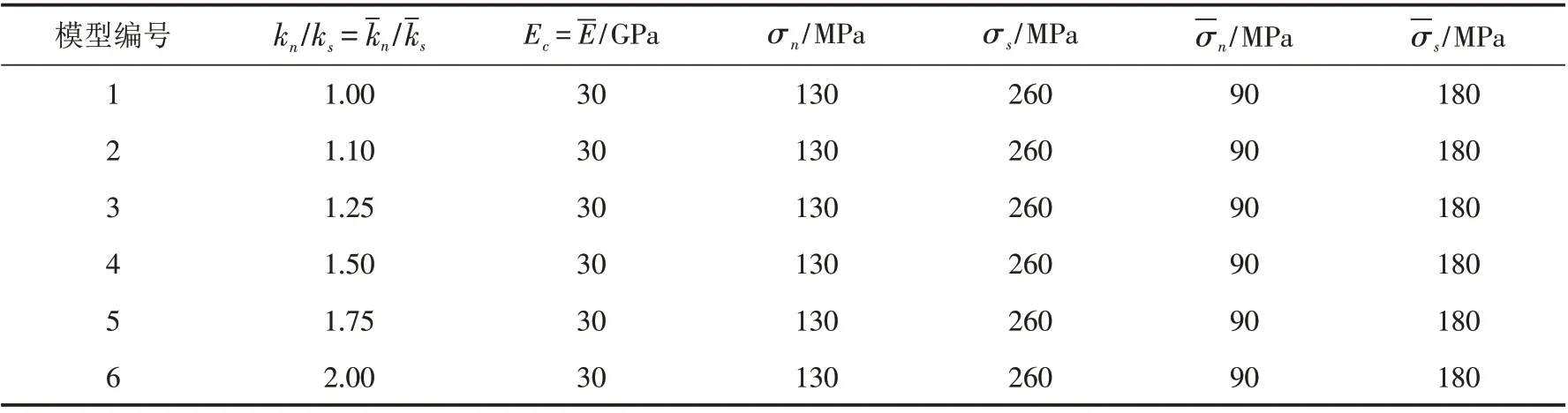
表1 kn/ks 对宏观参数影响模拟的微观参数组合Tab.1 Micro-parameter combination of the simulation of the influence of kn/ks on macro-parameters

图4 kn/ks 变化对宏观参数的影响Fig.4 The influence of kn/ks changes on macro parameters
1.2 Ec 和-Ec 对宏观参数的影响
保持其他微观参数不变,使各模型的Ec=-Ec在20~40 GPa内递增变化,如表2所示.

表2 Ec 对宏观参数影响模拟的微观参数组合Tab.2 Micro-parameter combination of the simulation of the influence of Ec on macro-parameters

1.3 σs 和σn 对宏观参数的影响
保持σs/σn=2 和其他微观参数不变,使各模型的σn在100~160 MPa内递增变化,如表3所示.

图5 Ec 变化对宏观参数的影响Fig.5 The influence of Ec changes on macro parameters

表3 σs 和σn 对宏观参数影响模拟的微观参数组合Tab.3 Micro-parameter combination of the simulation of the influence of σs and σn on macro-parameters
各个模型得到的宏观参数如图6所示. 可以看出σs和σn同时增大对E和ν几乎没有影响;UCS和TS随着σs和σn的线性增大近似线性增大,UCS 的最大变化为42.555 MPa,最大变化比(UCS 最大变化值与UCS最小值的比)为30.25%,TS 的最大变化为3.862 MPa,最大变化比(TS 最大变化值与TS 最小值的比)为19.15%,可以看出σs和σn的变化对UCS的影响比对TS的影响大.
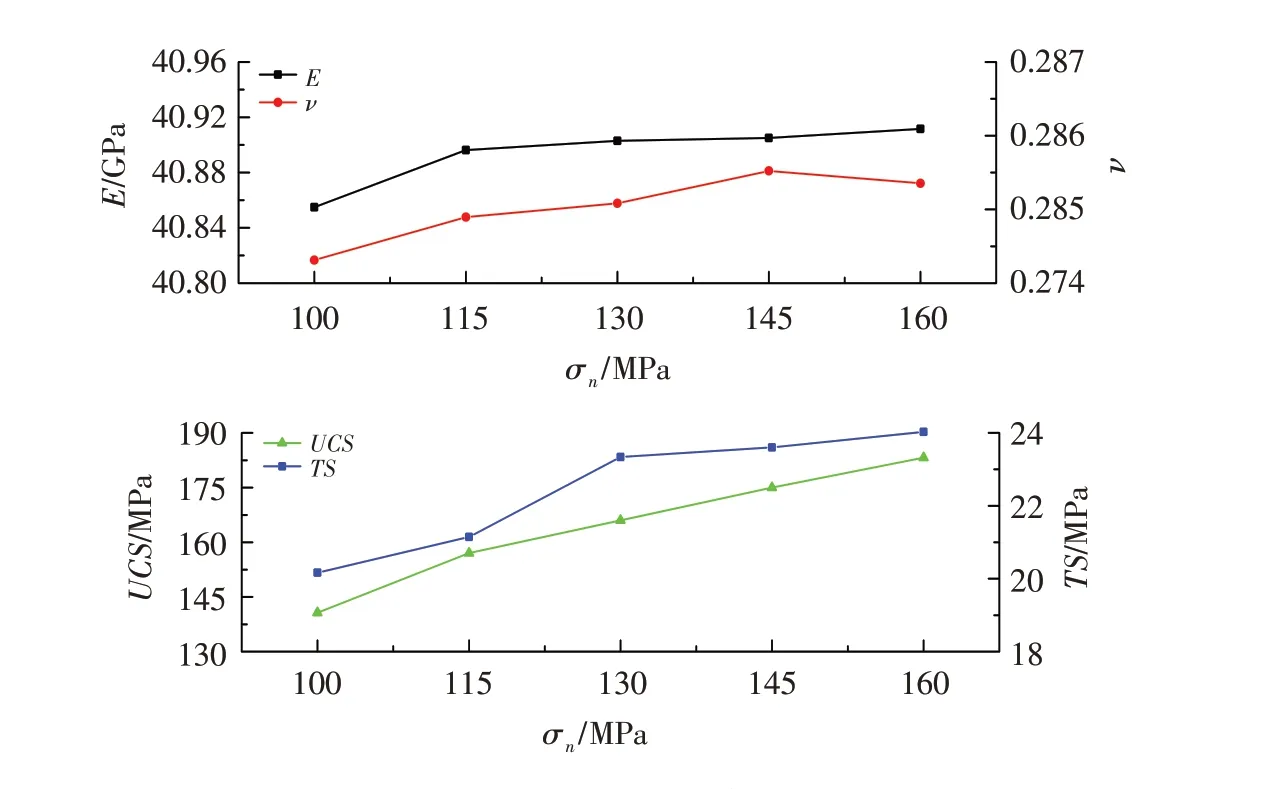
图6 σs 和σn 对宏观参数影响Fig.6 The influence of σs and σn changes on macro parameters
1.4 -σs 和-σn 对宏观参数的影响


表4 -σs 和-σn 对宏观参数影响模拟的微观参数组合Tab.4 Micro-parameter combination of the simulation of the influence of -σs and -σn on macro-parameters


图7 -σs 和-σn 变化对宏观参数的影响Fig.7 The influence of changes in -σs and -σn on macroscopic parameters
1.5 脆性簇平行黏结模型标定流程
前人研究分析表明微观参数的变化对宏观参数的影响是不同的,本节据此对脆性簇平行黏结模型提出一种先单一调整后组合微调、先近似后精确的标定流程(图8):
1)根据泊松比ν和图4选择kn/ks=k-n/k-s的值使模拟材料的泊松比与真实材料的泊松比基本一致;


4)成比例调整σs和σn使模拟材料的UCS与真实材料的UCS基本一致;
5)综合考虑各个微观参数变化对宏观参数的影响趋势及大小,选择所有微观参数中的几个值组合微调,实现对宏观参数的精确标定.
2 花岗岩宏观参数的标定及室内试验破坏过程研究
2.1 花岗岩室内试验及标定

图8 脆性簇平行黏结模型标定流程Fig.8 Calibration process of brittle cluster parallel bonding model
某高铁隧道山体为花岗岩,现场钻取直径D为55 mm,高h为110 mm和直径D为50 mm,高h为25 mm的圆柱体试样,采用RMT301岩石试验机分别进行单轴压缩和巴西劈裂试验,测得该花岗岩的宏观力学参数.根据本文提出的标定流程,对该花岗岩进行标定,标定过程的几组微观参数如表5所示. 各组微观参数标定得到的宏观力学参数与室内试验得到的宏观力学参数如表6所示,对式(5)的权重系数均取为0.25,得到各个模型的总相对标定误差.
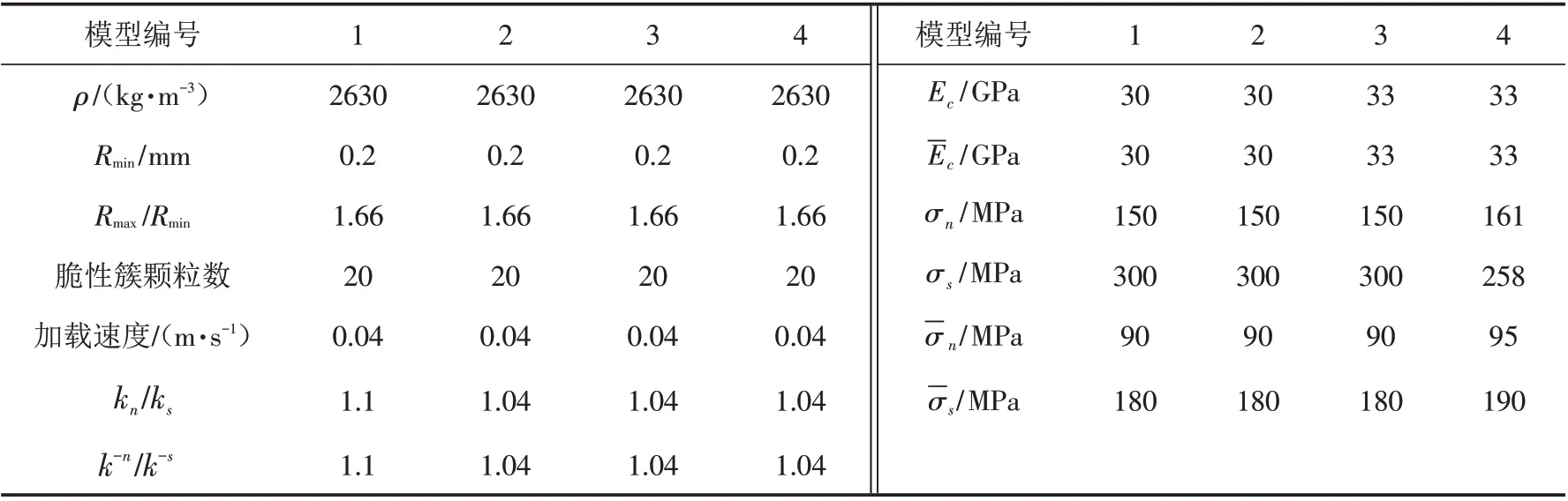
表5 基于脆性簇平行黏结模型标定的花岗岩模型微观参数Tab.5 Microscopic parameters of the granite model calibrated based on the brittle cluster parallel bond model

表6 某高铁隧道花岗岩室内试验与模拟得到的宏观力学参数Tab.6 Macro-mechanical parameters obtained from indoor test and simulation of granite in a high-speed railway tunnel
由表6可以看出,模型4的标定效果最好,对模型4的加载破坏过程进行分析. 单轴压缩和巴西劈裂的室内试验和颗粒流模拟(白色为张拉裂缝,红色为剪切裂缝)的最终破坏形态如图9所示,可见模拟的破坏形态与室内试验的破坏形态较为一致.

图9 单轴压缩和巴西劈裂室内试验和模拟破坏形态Fig.9 Laboratory test and simulated failure mode of uniaxial compression and Brazil split
2.2 室内试验和PFC模拟加载破坏过程对比分析
不少学者应用声发射技术研究花岗岩室内单轴压缩破坏过程[19-21],本文采用声发射技术监测花岗岩单轴压缩试验中裂纹的生成过程,与PFC模拟的单轴压缩过程对比. 室内单轴压缩与巴西劈裂试验加载过程应力应变曲线如图10所示,PFC模拟的单轴压缩与巴西劈裂过程应力、总裂纹数量、张拉裂纹数量、剪切裂纹数量随应变的变化曲线如图11所示. 模拟得到的加载曲线均表现出了花岗岩峰值强度后的脆断性.
巴西劈裂模拟的应力应变曲线在峰值应力前有两个明显的应力骤减阶段,分别截取两个应力骤减阶段开始和结束时微观破坏形态如图12所示. 可以发现第一个应力骤减阶段是巴西圆盘表面晶粒破碎后,模型沿晶粒接触边界断裂;第二个应力骤减阶段是巴西圆盘表面晶粒的穿晶断裂. 岩石破坏过程中破裂面总是沿着所需力最小的路径产生,巴西劈裂模拟应力应变曲线峰值应力前的两个应力骤减阶段表现出了破坏过程中破坏模式的选择.

图10 单轴压缩和巴西劈裂室内试验应力应变曲线Fig.10 Stress-strain curve of uniaxial compression and Brazilian split laboratory test
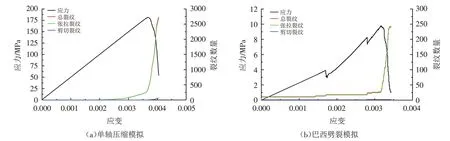
图11 单轴压缩与巴西劈裂模拟过程应力、总裂纹数量、张拉裂纹数量、剪切裂纹数量随应变的变化曲线Fig.11 Changes stress,total number of cracks,number of tension cracks,and number of shear cracks versus strains during uniaxial compression and Brazilian splitting simulation process

图12 巴西劈裂模拟两个应力骤减阶段开始和结束时的微观破坏形态Fig.12 The microscopic failure patterns at the beginning and end of the two stress reduction phases simulated by Brazilian splitting
图13的(a)~(e)为室内单轴压缩试验声发射监测和模拟过程的裂纹生成情况(声发射监测中红色为裂纹),可见各个阶段的破坏形态较为一致,验证了模拟过程的可靠性:
(a)裂纹萌生. 该阶段裂纹总数量约为峰值应力时裂纹总数量的2%,均为张拉裂纹,主要在试样靠近端部的地方产生,该阶段结束时应力约为110.17 MPa.
(b)裂纹扩展. 该阶段裂纹总数量约为峰值应力时裂纹总数量的10%,均为张拉裂纹,靠近试样端部的地方较密集,一些距离较近的裂纹开始形成宏观微裂纹,该阶段结束时应力约为136.54 MPa.
(c)中心裂纹萌生. 该阶段裂纹总数量约为峰值应力时裂纹总数量的50%,均为张拉裂纹,试样中部生成较多的裂纹,形成宏观微裂纹,该阶段结束时应力约为172.31 MPa,为峰值应力的94.79%.
(d)裂纹聚结. 该阶段裂纹总数量为峰值应力时裂纹总数量的100%,微裂纹开始聚结连通,在张拉裂纹最密集的地方开始出现少量剪切裂纹,该阶段结束时应力约为181.78 MPa.

图13 单轴压缩裂纹生成过程声发射监测与模拟过程生成裂纹对比Fig.13 Comparison of acoustic emission monitoring and simulation process of crack formation during uniaxial compression
(e)峰后失效. 微裂纹急剧增加,相互连通形成主裂缝,试样完全破坏,沿主裂缝附近形成较多的剪切裂缝,应力急剧减小,表现出明显的峰后脆性.
3 结论
本文研究了脆性簇平行黏结模型中主要微观参数对宏观参数的影响,并对某高铁隧道的花岗岩进行了标定,主要得出以下结论.
1)随颗粒刚度比和接触刚度比增加,宏观参数中弹性模量近似线性减小,泊松比近似线性增加;随颗粒接触模量和平行黏结模量增加,宏观参数中弹性模量近似线性增加,泊松比几乎不变.
2)簇内部颗粒间法向黏结强度和切向黏结强度增加,对宏观参数中弹性模量和泊松比几乎没有影响,对UCS的影响大于对TS的影响;簇间颗粒法向黏结强度和切向黏结强度增加,对宏观参数中弹性模量和泊松比几乎没有影响,对TS的影响大于对UCS的影响.
3)提出了脆性簇平行黏结模型用于脆性岩体模拟的一种新的标定流程:①调整kn/ks=k-n/k-s标定ν;②调整Ec=-Ec标定E;③成比例调整-σs和-σn,标定TS;④成比例调整σs和σn标定UCS;⑤根据E、ν、UCS、TS和图4~图7对微观参数中的几个值组合微调.
4)对某高铁隧道花岗岩的标定和破坏过程的研究验证了本文提出的标定流程的有效性和脆性簇平行黏结模型模拟过程的可靠性.

