双馈风力发电系统中变桨距线性自抗扰控制系统研究
李华柏, 谢永超, 胡 扬
(湖南铁道职业技术学院,湖南株洲 412001)
双馈异步电机在风力发电系统中应用很广泛. 风力机将风能转换成机械能,双馈电机将机械能转化为电能. 双馈电机包含两套极数不同的绕组,定子绕组(功率绕组)通过变压器与电网直接相连,转子绕组(控制绕组)连接双向变流器,经变压器与电网相连[1-2].
风力机捕获的风能取决于风速与桨距角,因此根据风速调节桨距角,使风力机始终能捕获最大风能,实现最大功率输出. 根据风力发电机的运行特性,可以分为最大功率追踪区、恒转速区、恒功率区.
当风速大于切入风速、小于额定风速时,为最大功率追踪区. 为了使风力机捕获最大风能,固定桨距角θ=0°并保持不变,调节风轮转速使风力机工作在最佳叶尖速比,系统进行最大功率追踪,捕获最大风能,输出即时风速对应的最大功率.
当发电机转速达到额定转速后,发电机进入恒转速运行,进入恒转速区. 随着风速增加,风能利用系数减小,输出功率增加至额定功率.
当风速大于额定风速后,进入恒功率区,为保护发电系统,调节叶片攻角,实现变桨距控制,限制风轮捕获风能,使风轮与发电机维持在额定转速运行,系统输出额定发电功率.
针对双馈风电机组的功率控制研究,文献[1]采用自适应遗传和模糊布谷鸟算法整定的自抗扰控制技术,改善了风电机组的控制性能[1]. 文献[2]采用基于改进灰狼算法的线性自抗扰技术对变桨距系统进行控制[2]. 文献[3]提出最佳叶尖速比的自抗扰控制策略,实现最大功率跟踪控制[3]. 滑模变结构控制[4]、模糊逻辑控制[5]应用到风电系统功率控制,也取得了较好的效果. 考虑桨叶的较大惯性,模糊前馈控制主要根据风速的检测输入量给出桨距角模糊前馈变化量[6]. 自抗扰控制器具有良好的抗扰性能,适合无法建立精确数学模型的复杂非线性系统,在风电系统的恒功率控制、变桨距控制、最大功率追踪、最大风能捕获方面取得了良好的控制效果[7-20].
本文针对风电系统在恒功率区的功率控制进行分析与研究,当风力机转速大于额定转速时,将线性自抗扰控制器(LADRC)应用于风力发电系统的变桨距控制,实现输出功率的稳定,防止风力发电机过载运行.为验证所设计控制方法的有效性,与PID控制进行了对比仿真研究.
1 变浆距线性自抗扰控制器设计
1.1 双馈发电系统传动机构数学模型
风轮及主轴的动力学方程可表示为

双馈发电机转子的动力方程为

其中:齿轮传动比为n=ωr/ω .
将式(2)代入(1)可得

式中:Ja与Jg分别为风轮与发动机转动惯量;ω、Ta为风轮转速与转矩;ωr、Te为发电机转速与电磁转矩;Td为阻力矩;n为齿轮箱传动比;Tg为发电机传递给齿轮箱的转矩.
1.2 变桨系统的LADRC数学模型
取风电机组恒功率运行时的一个平衡点A,该点参数为Ta0、θ0,则函数Ta( ω,θ,v )在A点处的泰勒展开式为[7-9]
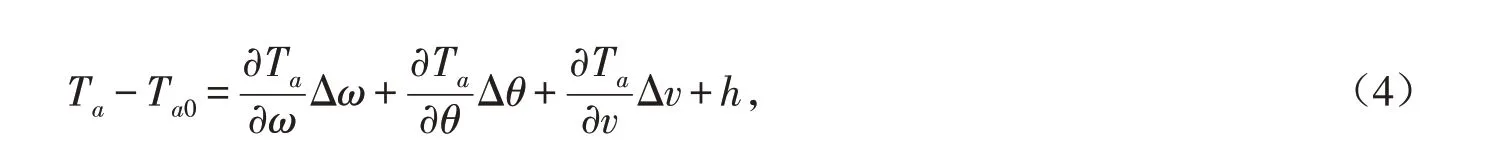
式(4)中,h为展开式高次项. 设:

则

由式(3),在额定风速以上运行,风轮与发电机维持恒定转速,因此

令J=Ja+n2Jg,由式(5)、(6)、(7)可得

其中:h为展开式高次项.
由桨距角的动态特性,可得

其中:θa为桨距角给定值;τ 为时间常数;s为拉氏变换中的复参变量.
由式(7)、(8)、(9)可得
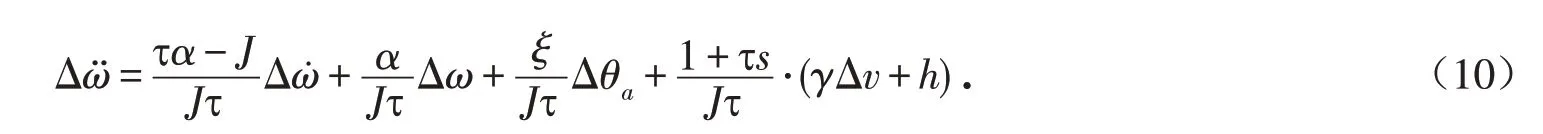
b0是控制量Δθa增益b的估计值,取为

那么系统总扰动量f 可表示为
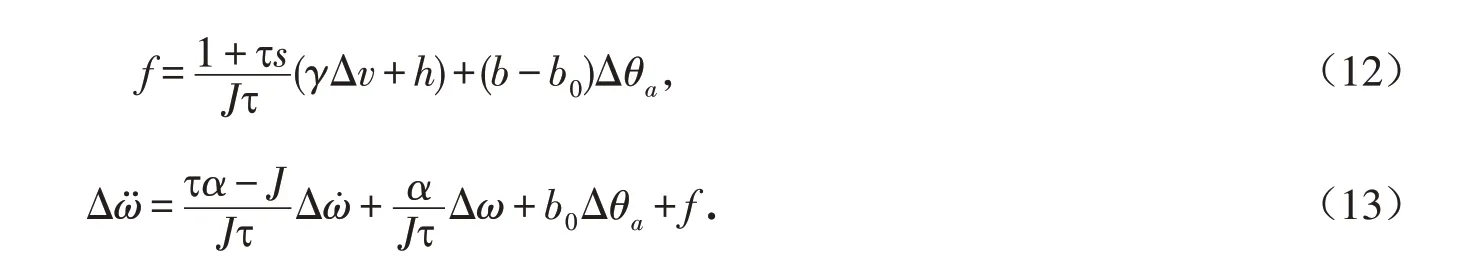
式(13)是变桨距控制系统数学模型,以此来设计线性变桨距自抗扰控制器.
1.3 变桨距LADRC控制器设计
自抗扰控制器(ADRC)具有良好的抗扰性能,但是在非线性反馈下,需要整定的参数多,整定过程复杂.本文对非线性自抗扰控制器进行了线性化处理.
LADRC 主要由跟踪微分器TD、线性状态观测器ESO和比例微分控制器组成. 它采用线性函数代替了ADRC中的非线性部分,既保持自抗扰控制器的特性,又简化了需整定的参数.
1.3.1 线性扩张状态观测器 令y=Δω,u=Δθa,x1=y,x2=y′,式(13)转化为空间状态方程并进行扩张:
编者按:落实最严格水资源管理制度,是水利工作的重中之重。水利部印发《关于开展加快实施最严格水资源管理制度试点工作通知》,举全部和全系统之力,积极推进最严格水资源管理制度试点工作,旨在先行先试、以点带面。各试点省、市、流域因地制宜,突出特色,按照“四个率先”的总体要求,积极践行最严格水资源管理制度,切实推行各项试点任务,在建设中进行探索与实践,成效与亮点逐步显现,有力促进了水资源节约保护与管理工作。本期特别策划“加快实施最严格水资源管理制度试点专题”,总结分析各试点地区好的做法和经验,探讨试点工作中的关键环节和核心问题,为全国进一步推进最严格水资源管理制度工作的落实提供有益借鉴。

式(14)的线性状态观测器表达式为

式中:zi为xi(i=1,2,3)的观测值.
按极点配置方法,求得式(15)的特征方程为

选取理想特征方程:

得

式中:ω0观测器带宽. 观测器增益矩阵[ ]β1,β2,β3控制观测器的准确性,而状态观测器的准确性决定了前馈补偿量的大小. 由式(18)可知,状态观测值的准确性由带宽ω0决定.
1.3.2 误差反馈PD控制器 对于二阶系统,控制输入量为

则


其中:[kd,kp]构成反馈增益矩阵,式(21)的特征多项式为


线性自抗扰控制器结构如图1所示. r为参考输入,u与y分别为系统的输入与输出.
1.3.3 带模糊前馈LADRC变桨距控制系统设计 当风速高于额定转速时,双馈电机实际发电功率高于额定功率,比较二者的偏差,并根据扩张状态观测器估计系统总扰动,实施前馈补偿,得出桨距角控制信号,实现恒定功率输出. 但风轮的桨叶具有较大的惯性,可能导致LADRC前馈补偿相应滞后,影响前馈补偿控制效果. 因此在LADRC控制的基础上增加了模糊前馈控制器.
模糊前馈控制器主要考虑桨叶的较大惯性,根据风速的检测输入量给出桨距角模糊前馈变化量θf,与LADRC输出的桨距角给定值θa相加,作为最终的桨距角设定值θr. 当检测到风速变大时,θr为正,增大桨距角给定值,反之,减小桨距角给定值. 根据风轮的桨叶特性,在不同的风速下,风速变化需要的桨距角变化量是不同的,风速越大,较小的桨距角变化量就能维持风力机转速的恒定,因此模糊前馈控制器设计了两个输入量[6].
输入量1为检测风速值v(k-1)与v(k). 本文中,vN=12 m/s,vout=24 m/s. 输入量1的基本论域为[12,24],对应的模糊论域为{1,2,3,4,5}.
输入量2为风速误差Δv,决定前馈桨距角θf的变化量. 输入量2的基本论域为[-3,3],对应的模糊论域为{-3,-2,-1,0,1,2,3}.
基于模糊前馈补偿的LADRC变桨距控制器如图2所示.

图1 线性自抗扰控制器结构Fig.1 Structure of LADRC
2 仿真验证

图2 LADRC改进型变桨距控制系统原理Fig.2 Principle of LADRC pitch control system
线性自抗扰控制参数设置如下:ω0=20,ωc=5,b0=10 .
双馈风力发电系统的仿真参数设置如下:vN=12 m/s,CP=0.5,Ja=3.2×105kg·m2,τ=0.2.
发电机参数设置如下:UN=220 V,PN=20 kW,nN=1500 r/min,Jg=3.5×105kg·m2.
图3验证随机风条件下系统的最大功率输出性能,随机风在0~20 s 风速平均值约11 m/s 左右,小于额定风速,此时桨叶最大限度打开,桨距角为0,按最佳功率曲线进行最大功率追踪,输出即时风速下的最大功率,Cp基本保持在0.45左右. 20 s以后,v>vN,为了防止双馈发电机超负荷运转,此时通过调节桨距角,对风力机的转速进行控制,双馈发电机输出功率在20 kW左右,基本维持额定功率运行.
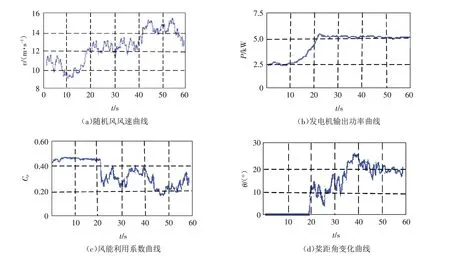
图3 随机风条件下仿真波形Fig.3 Simulation waveforms under random wind condition
图3表明,在随机风的多变干扰下,当,v>vN,桨距角随着风速的增大而减小,使风轮维持恒定转速运行,输出恒定功率,表明LADRC桨距角控制器面对随机风的变化,仍然能取得良好的抗扰性能.
图4 中,0~22 s 时随机风平均值约12 m/s,22 s以后,平均值约9 m/s. 对比分析可知,LADRC 控制方式下,系统的响应速度优于PID控制器,输出功率的稳定性稍好于PID 控制方式,验证了自抗扰控制器对随机风扰动抗扰的有效性.

图4 随机风下PID与LADRC功率响应曲线对比Fig.4 Comparison of power response curves between PID and LADRC
随机风情况下的仿真分析表明,一方面,LADRC基本继承了ADRC 抗扰性能强的特性,能够达到风力发电系统最大功率输出的目标;另一方面,与传统的PID控制方法相比,LADRC具有更好的转速跟踪性能、更小的超调量、更快的响应速度,因为ESO能够实时地对系统的风速扰动进行实时估计并及时进行主动补偿,使得系统跟踪性能更好.
3 结论
本文设计了基于线性自抗扰控制的双馈发电系统的恒功率区变桨距控制策略,建立了变桨控制LADRC控制模型. 得出以下结论.
1)恒功率区,风速大于额定风速,将LADRC应用于变桨距控制系统,通过对风速变化的实时估计与补偿作用,调节桨距角实现恒功率输出.
2)在LADRC的基础上,增加了模糊前馈补偿,较好地解决了由于桨叶的大惯性特性引起的前馈补偿滞后.
3)仿真结果表明,与传统的PID控制方法相比较,LADRC能有效地抑制内外扰动对风力机转速的影响,实现双馈风力发电功率的有效控制.

