复合材料螺栓干涉连接摩擦系数影响研究

单金洋　杨淳凯　赵耀斌　武涛

摘 要：干涉连接有助于改善机械连接接头的力学性能，在金属构件中得到了广泛应用，并逐渐推广至复合材料。干涉连接的螺栓初始直径大于孔径，通过螺杆与孔的装配在孔周产生干涉应力，从而改变连接接头在承力时的应力状态。干涉应力的分布不仅与螺栓和孔的材料有关，还受界面摩擦力的影响。本文以碳纤维增强和玻璃纤维增强树脂复合材料为对象，建立螺栓干涉连接有限元模型，对界面摩擦系数分别为0、0.1和0.2时的孔周应力进行分析。研究结果表明：摩擦系数对孔周径向应力和周向应力的分布趋势影响较小，对数值影响较大;减小摩擦系数有助于降低周向应力水平，但会引起径向挤压应力水平的上升。

关键词：复合材料;干涉连接;应力分布;摩擦系数

中图分类号：TB332 文献标识码：A 文章编号：1003-5168（2021）25-0037-04

Study on the Influence of Friction Coefficient of Composite Bolt Interference Connection

SHAN Jinyang YANG Chunkai ZHAO Yaobin WUTao

（1.School of Transportation Science and Engineering，Civil Aviation University of China，Tianjin 300300;2.China Railway Beijing Bureau Group Tianjin Station， Tianjin 300353）

Abstract： The interference fit technique is believed to be helpful in improving the mechanical properties of bolts， which are widely used in metal components and extended to composite materials. The initial diameter of the bolt is larger than the hole. So the interference stress is produced around the hole after components assembling， then the stress state of the joint is changed. However， the distribution of interference stress is related to the material and interfacial friction， which should be noticed in analysis. In this paper， the finite element model of interference fit bolted joint is built for carbon fiber reinforced and glass fiber reinforced resin composites. The stress around the hole is analyzed when the interface friction coefficient is 0、0.1 and 0.2. The results show that the friction coefficient has little influence on the distribution trend of the radial stress and circumferential stress， but has obvious effects on the value. The decrease of friction coefficient could reduce the circumferential stress level， but it will cause the increase of the radial extrusion stress level.

Keywords： composite;interference fit;stress distribution;friction coefficient

隨着复合材料在航空、航天、汽车等领域的广泛应用，其结构的安全性日渐成为研究热点。复合材料结构在应用中因工艺和使用的限制，需要配备连接接头，而这些区域往往是结构中易发生应力集中和损伤的部位。螺栓连接因承载能力强、易于拆卸等优点，成为复合材料主要的连接方式之一。干涉连接是采用过盈配合的连接形式，通过螺杆与孔壁的相互挤压在复合材料孔周形成装配后即存在的干涉应力。研究表明，该种连接方式有助于提高接头的疲劳寿命等机械力学性能[1-2]。

由于干涉连接中未变形的螺栓杆直径大于未变形的孔直径，因此其主要存在两种安装方式，即直接压入式和螺栓膨胀式。螺栓直接压入式的工艺条件比较简单，因干涉量变形集中发生在安装接触表面，且引入了厚度方向的作用力，其应力状态相对而言更加复杂，也更容易导致装配缺陷[3-4]。膨胀式的变形主要是板平面内的杆孔变形协调，可通过控温等方式实现。然而，无论使用哪种工艺方式，螺栓杆与孔的变形关系在装配时都会引起接触摩擦，并在界面处产生抑制相互运动的作用力，从而影响干涉连接杆孔表面的变形及应力的分布。掌握界面摩擦系数对孔周应力分布与数值规律的影响，对结构的强度及寿命预测、安全性分析以及工艺优化均有重要意义。本文以常见的碳纤维增强复合材料（Carbon Fiber Reinforced Polymer，CFRP）和玻璃纤维增强复合材料（Glass Fiber Reinforced Polymer，GFRP）层合板为对象建立有限元模型，分析不同摩擦系数下孔周径向应力与周向应力的分布，揭示摩擦系数对干涉连接应力分布的影响规律。

1 有限元模型

在通用有限元分析软件ABAQUS中建立复合材料板干涉连接模型，建立的有限元模型如图1所示。模型包括复合材料板和螺栓两个部件，通过界面接触设置模拟膨胀方式实现干涉配合。考虑到螺母、螺栓等结构不参与杆孔之间的变形，为便于计算，将螺栓简化为杆。初始状态孔径[r]与杆径[R]相同，均为6 mm;在后续分析步中设置接触面干涉量[Δ=R-r]=0.03 mm。使用面面接触的方式，螺杆为主面，孔壁为从面。螺栓杆长6 mm。为减少边界效应对应力的影响，设置板的形状为正方形（36 mm×36 mm），板厚度为2 mm。

板的材料使用CFRP和GFRP两种。不同铺层方向的邻层之间会产生应变协调，为便于进行应力规律的分析，在属性设置中将铺层设置为单向铺层[5]。螺栓为钛合金TC4。孔周是应力集中区域，是应力分析关注的重点。为在减少计算代价的同时尽可能保证精度，将复合材料板划分区域，孔周采用密度更高的网格，网格类型为C3D8I;板外侧则用密度较低的网格，网格类型为C3D8R。螺栓与孔壁接触，故其网格密度设置与孔周接近。几何约束的设置如图1所示，板的四周端面为全约束，模拟板的加持，螺栓中线约束其各向运动。

2 结果与分析

由于材料的各向异性，各方向应力分量的物理含义不能完全等效，不宜使用米塞斯应力详细分析所涉及区域的应力变化。考虑到结构区域几何形状的特点，选择以孔中心为圆心建立圆柱坐标系，沿纤维0°方向为[R]轴，厚度方向为[Z]轴。各层材料在螺杆与板孔的挤压交互过程中会发生变形，在板平面上各層的几何和受力条件都较为接近;而在厚度即[Z]方向，由于受上下表面的边界效应影响，各层应力数值有一定的差异。实际上结构区域损伤与性能的决定性因素是应力集中区，故在规律分析时选择应力水平较高的表面层，沿孔周选取节点。考虑到结构及变形关系的对称性，选取半圆路径，并输出应力数值进行分析。

2.1 CFRP板干涉连接孔周应力

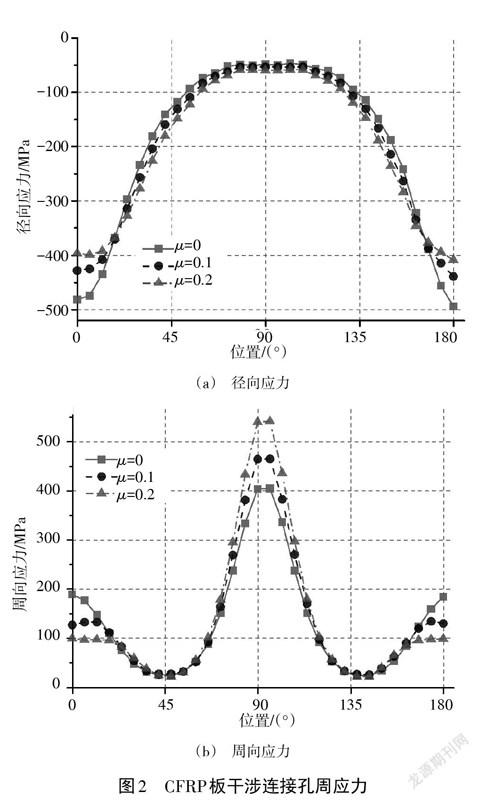
CFRP板干涉连接孔周应力摩擦系数影响结果如图2所示，其中图2（a）是径向应力的对比结果，图2（b）是周向应力的对比结果。由图2可知，螺杆与孔壁摩擦系数对孔周应力分布形式的影响较小，摩擦系数[μ]分别为0、0.1和0.2时，径向应力与周向应力的曲线变化趋势基本相同，部分邻近节点间数值的微小波动与有限元建模的网格密度设置有关。

径向应力的数值为负值，该结果与干涉连接螺杆和孔壁挤压的几何变形条件有关，即孔周区域节点处的径向应力均表现为压应力。曲线的整体形状呈单峰波浪形，但考虑到应力数值为负，发生应力集中的区域应为曲线的两端。曲线整体沿90°位置对称分布，以0°～90°为例，对3种摩擦系数条件下的径向应力数值作对比分析。3种摩擦系数条件下径向应力曲线均在0°位置取最低点，即沿孔周各节点中径向应力与纤维方向平行的节点，径向应力绝对值最大;在90°位置数值最大，即径向应力与纤维方向垂直的节点，径向应力绝对值最小。在0°和180°位置，3种摩擦系数所得结果中：摩擦系数[μ]为0时径向应力绝对值最大，径向应力约为-480 MPa;摩擦系数[μ]为0.1时，径向应力绝对值次之，径向应力约为-425 MPa;摩擦系数[μ]为0.2时，径向应力绝对值最小，径向应力约为-396 MPa。可见，摩擦系数增大降低了径向应力的峰值水平。在20°位置，3种条件下的径向应力差值显著减小，在20°～90°位置，摩擦系数与径向应力绝对值成正比。在90°位置，3种摩擦系数条件下的径向应力计算结果较为接近，约为-50 MPa。沿孔周的径向应力数值整体呈现较大波动，在[μ]为0时，应力的峰幅值差异将近10倍，而[μ]为0.2时，该比例也达近8倍。

周向应力的数值为正值，该结果与干涉配合孔壁在螺杆作用下扩张的几何变形条件一致，即孔周区域节点处的周向应力均表现为拉应力。曲线整体形状存在3个峰值，分别在0°、45°和90°位置。曲线整体沿90°位置对称分布，同样以0°～90°范围为例对3种摩擦系数条件下的周向应力数值作对比分析。3种情况下曲线均在90°位置取极大值，且数值远大于0°的次峰值，即在周向应力方向与纤维方向平行的节点处，周向应力最大。其中：摩擦系数[μ]为0时周向应力较其他两种条件更低，约为400 MPa;摩擦系数μ为0.2时，周向应力数值最大，约为540 MPa;[μ]为0.1时周向应力数值次之，约为465 MPa。周向应力的数值与摩擦系数成正相关，该种关系在45°～90°均存在，但3种条件之间的结果差距则随着角度的减小而逐渐降低。周向应力在45°位置到达低谷，取最小值，3种条件的结果非常接近，约为25 MPa，说明在45°位置附近摩擦系数对周向应力数值的影响微弱。在0°～45°内3种曲线的数值规律与45°～90°内的规律相反，周向应力的数值与摩擦系数[μ]成反比关系，在0°位置曲线出现次峰值，而摩擦系数[μ]为0的曲线数值最大约为189 MPa;[μ]为0.1的曲线最大数值次之，约为126 MPa，[μ]为0.2曲线最大数值最小，约为99 MPa。

2.2 GFRP板干涉连接孔周应力

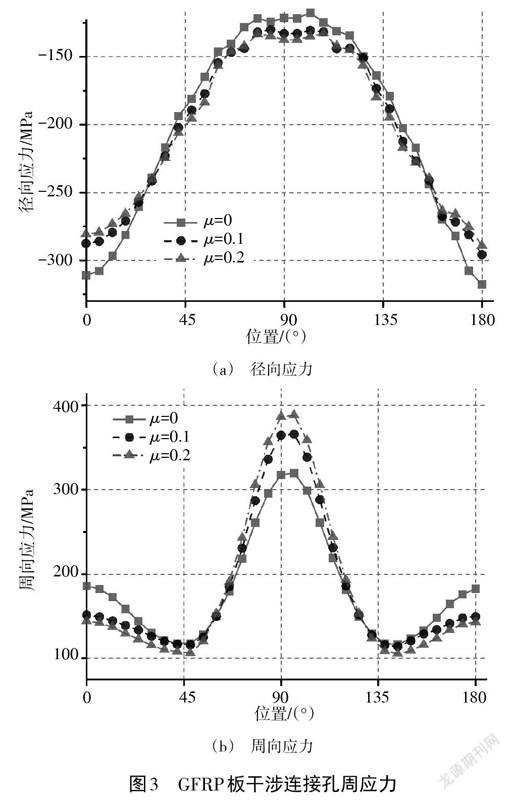
GFRP板干涉连接的计算结果如图3所示，其中图3（a）是径向应力，图3（b）是周向应力，均包括摩擦系数[μ]等于0、0.1和0.2条件下的3条曲线。对比图2可知，摩擦系数对GFRP板干涉连接孔周应力分布趋势的影响与CFRP板的情况相同，3种条件下的整体曲线形状基本一致。然而，由于GFRP材料的各向异性系数较CFRP板更小，应力数值的取值范围也较CFRP的结果更小。

径向应力整体规律与图2的CFRP算例结果规律相似，在0°和180°处有最大绝对值，而[μ]为0时的应力绝对值明显超过[μ]为0.1和0.2时。在0°～25°内，摩擦系数越小，径向应力的绝对值越大。3条曲线均在90°附近取得最小绝对值，且90°附近的数值变化也较小，数值约为-130 MPa。在该范围内，3条曲线的数值略有差异，无摩擦时的绝对值始终最小。[μ]为0时，径向应力最大最小值之比约为2.5，[μ]为0.1时该比例约为2.2，[μ]为0.1时该比例约为2.1。

周向应力的曲线最高峰值出现在90°附近，另有两个次峰值在0°和180°，波谷极小值出现在45°和135°，整体规律与CFRP的结果相同。在中央峰区域，摩擦系数与应力数值成正相关，3条曲线的差距在90°附近最大，数值分别为319 MPa、366 MPa和388 MPa。而在其余区域，应力数值则与摩擦系数成负相关，无摩擦时的周向应力值高于有摩擦时，[μ]取0.1和0.2时的结果都较为接近，应力最小值约为110 MPa。

2.3 摩擦系数对孔周应力的影响分析

对比上述两种材料的结果可以发现，摩擦系数对孔周径向和周向应力的整体分布趋势没有明显影响，这是因为干涉连接形成的孔周应力主要由螺杆与孔壁相互挤压配合而成。对于采用膨胀螺杆方式安装的干涉连接，螺栓与孔几何半径的差距主要由平面内螺栓与板孔的径向变形共同分担。该变形与材料的模量大小共同决定应力的整体趋势，与摩擦力关系较小。

然而，摩擦系数对应力数值则有较大影响，且对CFRP和GFRP兩种材料的影响规律较为接近。受材料纤维增强复合材料特征的影响，在沿纤维方向板材的模量较大，而垂直纤维方向的模量较小，从而导致孔周各点的变形有所差异，各点实际存在剪应力和相互间变形协调的关系。图2和图3中0°和180°位置出现的径向应力与90°位置出现的周向应力峰值，在笛卡尔坐标系下则均为沿[X]方向的应力分量，即这些位置沿纤维方向的应力分量，其应力水平较高而正负不同。孔周各点的应力水平和形变差异会引起一定的沿环向位移，直至达到平衡状态，而摩擦力则在一定程度上阻碍这种应力状态的均匀化。在结果中表现为无摩擦作用时，径向应力与周向应力的绝对数值更为接近;而增加摩擦系数时，两个应力分量的差异则相应增加。

孔周的应力集中区域往往是材料损伤的发生区域，应力水平的提高会影响结构后续的加载响应和结构的服役表现。对于采用膨胀方式的干涉连接结构而言，降低摩擦系数有助于孔周变形的协调，对平衡应力分布有一定的作用。但是，机械连接传递面内载荷主要是通过螺杆与孔壁的挤压变形，因而杆孔正挤压区域往往也是损伤发生的区域，适当提高摩擦系数，降低该区域的干涉预压应力，在不引起其他部位损伤的情况下可行。

3 结语

螺栓连接是常见的复合材料连接形式，采用干涉配合的螺栓连接通过在孔周引入预压应力可以改善结构的力学性能。本文建立有限元模型，以常见的CFRP和GFRP材料为对象，分析复合材料在使用干涉连接时孔周应力分量受摩擦系数的影响规律。结果表明，对于采用膨胀安装的干涉螺栓而言，螺栓杆与孔壁的摩擦系数并不影响孔周应力的整体分布，但对应力分量的数值则有显著影响。无摩擦条件下的径向压应力最大绝对值较有摩擦条件下更大，且该差距随摩擦系数的增大而增加，最大值出现在径向应力与纤维方向平行的位置;而周向应力最大值则随着摩擦系数的增大而减小，最大值出现在周向应力与纤维方向垂直的位置。降低摩擦系数有助于改善整体孔周应力的分布不均匀性，但适当增加摩擦系数将降低螺杆孔壁挤压面的压应力，有利于抑制该区域挤压损伤的发生。

参考文献：

[1]魏景超，柴亚南，刘风雷，等.单面螺纹抽钉干涉配合复合材料连接结构的疲劳性能研究[J].航空制造技术，2017（22）：50-55.

[2]宋旭峰.CFRP/AL叠层构件干涉连接结构力学行为研究[D].西安：西安理工大学，2019：38.

[3]蒲浩，李磊，熊华峰.紧固件类型及干涉配合对复合材料连接强度的影响研究[J].现代工业经济和信息化，2018（5）：19-22.

[4]宋丹龙，宋旭峰，白洋洋，等.碳纤维增强环氧树脂复合材料层合板干涉连接插钉轴向力建模与分析[J].复合材料学报，2019（10）：2294-2301.

[5]段元欣，程晖，刘平，等.复合材料干涉螺栓压入过程力学行为数值及试验分析[J].航空制造技术，2015（20）：64-68.

3931501908218