调整情境参量 锤炼关键能力

范玮逸 时子豪

摘   要：“导体棒切割磁感线”是高中物理电磁感应综合问题中的一类典型问题模型。文章首先分析归纳课内要求的导体棒在含电阻和含电源电路中受恒力作用下切割磁感线的受力情况与运动情况，求出导体棒的末速度。再基于解决物理问题的基本思路和方法，进一步调整“参量”，探讨将电阻替换为电容、电感后，导体棒的受力及运动情况，将导体棒在不同种类电路中切割磁感线问题进行深度剖析和对比总结。

关键词：切割磁感线;含电容电路;含电感电路

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2021）10-0057-4

1    “导体棒-电阻”模型

【模型描述】 如图1所示，一根质量为m的导体棒在重力作用下可以沿竖直放置的两根平行金属导轨下滑，在导轨上端接一个阻值为R的电阻，导轨间的距离为l，整个系统处在匀强磁场B中，其方向垂直于导轨平面向里。导体棒与两导轨始终保持垂直并良好接触，导轨及导体棒的电阻、回路的自感均忽略不计，讨论导体棒的运动情况并求棒最终稳定的速度。

【问题剖析】 由题目信息可知，导体棒会在重力作用下由静止开始运动，由于切割磁感线，导体棒产生动生电动势，回路中有感应电流产生，导体棒受到安培力的作用，经右手定则可判断动生电动势与导体棒中感应电流方向，再由左手定则判断导体棒受到竖直向上的安培力，如图2所示。

根据牛顿第二定律

2    “导体棒-电源”模型

【模型描述】 如图3所示，将图1中连接在导轨上端间的电阻换成电动势为E、内阻为r的电源，分析导体棒的运动情况以及棒最终稳定的速度。

3    “导体棒-电容”模型

【模型描述】 如图5所示，将图1中连接在导轨上端间的电阻替换为电容为C的电容器，试分析导体棒的运动情况。

【问题剖析】 电容器是存储电荷的元器件，其储存的电荷量与其两端电压及电容满足关系Q=CU。由于电容器并联在导体棒两端，故其切割磁感线产生的感应电动势即为电容器两端的电压，取某极短时间Δt，电流i满足关系

导体棒下滑过程中受到的安培力方向竖直向上，根据牛顿第二定律

分析（3）式可得，导体棒运动的加速度恒定，即导体棒在电容电路中受恒力作用切割磁感线时将以此加速度做匀加速直线运动。

（说明：此模型忽略了整个电路中的电阻，是對实际情境的一种中学合理化处理，若考虑电阻，可通过分析求解微分方程，进行详细讨论，在此不做详细过程推导。）

4    “导体棒-电感”模型

【模型描述】 如图6所示，将图1中连接在导轨上端间的电阻替换为电阻不计、自感系数为L的电感线圈，将导体棒由静止释放，试分析导体棒的运动情况。

【问题剖析】 相较于前三种模型，“导体棒-电感”模型在教学中一般不进行深入讨论，但对于物理基础较好、学有余力的尖子生或者在培优竞赛课上，可以将此模型进行深入探讨，培养学生用一般性物理方法解决新情境问题的能力。

（1）以导体棒受力为突破口猜测导体棒的运动情况

现规定：①出发点为坐标原点，则Δx=x-0;②导体棒刚开始运动时回路中电流为0，则ΔI=I-0。因此，上式可整理得Blx=LI，即回路中电流与导体棒位移成正比关系。

观察上式，导体棒受到一个恒力以及一个与位移成正比的变力作用。导体棒从静止开始运动，随着位移和速度的增大，加速度在减小，导体棒做加速度减小的加速运动，当加速度为0时，速度达到最大值，而后位移和速度继续增大，导体棒受到的安培力大于重力，加速度反向，导棒继续向下，做加速度增大的减速运动，当速度减为0时，此时加速度最大。

在面对和解决新情境问题时，应引导和鼓励学生结合已学过的典型的、重要的物理模型，进行模型迁移，将新情境与已学模型进行有效关联。此种运动情况，在高中物理的学习过程中并不陌生，最直接想到的应该是竖直方向弹簧振子模型。竖直方向弹簧振子受力为mg-kx=ma，弹簧振子做简谐运动。

（2）以竖直弹簧振子做类比证明导体棒做简谐运动

回顾以竖直弹簧振子为例，证明其满足回复力大小与位移成正比，方向与位移相反，振子做简谐运动。

类比上述证明方法，推理论证（1）中的猜测。

（3）根据简谐运动的运动特点确定导体棒运动情况

5    总结与反思

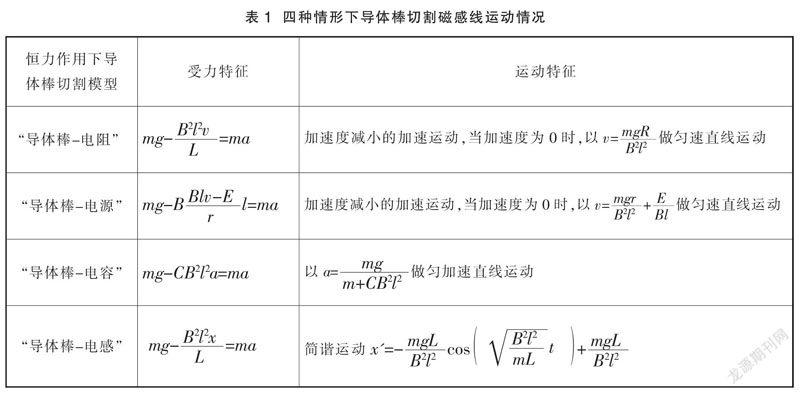
将四种情形下的导体棒切割磁感线情况进行比较（表1），回顾在探析这四类导体棒切割磁感线的运动情况问题时，我们均以核心规律——牛顿运动定律为出发点，根据电路中所连元器件的不同，依据其本身的性质，对导体棒的运动情况进行分析求解。求解过程中根据不同物理量的物理意义，辅以求导等数学手段，使求解思路更加清晰，过程更加简洁。

通过探析、比较，我们可以发现，电路中连接的不同元器件均是通过影响电路中电流的变化，进而影响金属棒受到的安培力大小来影响其的运动，例如电源使电路具有了初始电流;电容通过均匀充放电使电流恒定不变;电感则通过产生自感电动势使电路中产生了交变电流;使得导体棒分别做先变加速后匀速直线运动、匀加速直线运动、简谐运动。

这也给我们很大的启发，根据最近发展区理论，新问题在原有问题的基础上，可通过调整情境参量，增加一定难度，推动思维和能力的进阶，在探析过程中，引导学生解决类似问题时，从本质上理清题目中的变量，实现类似问题的情境转场，由表及里，运用核心规律、思想方法，分析解决问题，实现思维品质的提升与关键能力的锤炼。

（栏目编辑    罗琬华）

1192501705271