铁路退票险费率计算模型构建研究

王红爱，朱建生，陈 靖，张志强

（1.中国铁道科学研究院 研究生部，北京 100081；2.中国铁道科学研究院集团有限公司 电子计算技术研究所，北京 100081)

随着高速铁路的快速发展，铁路客票发售与预订系统(以下简称“客票系统”)不断推出新的业务模式，目前可以通过互联网、手机端、自助设备端、车站窗口和代售点窗口等不同渠道，提前进行车票预售。由于旅客行为的不确定性，可能出现办理退票或改签的情况，退票时按照阶梯退票费率的方法收取退票费，目前在很多行业(如航空)都有损失承担保险的退票险，尤其由于旅客自身原因退票产生损失时，可以为旅客承担一定比例的费用。随着铁路电子客票的全面推广，出现退票量居高不下的情况，研究铁路退票险不仅是弥补车票退票差价的一种保险，还可以分担旅客退票和铁路客运资源在合同约定履行时间内的违约风险，降低旅客由于退票而产生的经济损失，补偿铁路由于退票而造成的资源浪费。因此，通过借鉴交通运输行业的非寿险费率计算方法，选择合适的业务影响因素和计量模型，构建铁路退票险费率计算模型，形成针对不同风险类别的费率体系计算纯保费，推进铁路退票险费率研究进程。

1 非寿险费率计算方法

1.1 传统费率计算方法

退票险保费由纯保费和附加保费构成，纯保费为期望赔付的成本，附加保费包括经营费用和保险监管费用等。费率的影响因素是保险费率计算的基础，根据可能造成损失的风险大小来确定影响因素，而且不同的影响因素包括不同的分类特征。在保险费率计算时，传统的模型有加法模型和乘法模型[1]，依据影响因素分类特征作为费率目标函数的自变量，通过加法或者乘法进行费率迭代计算，可以采用边际总和法、最小二乘法和极大似然法等方法。这些费率计算方法的差异在于对目标函数的选择，如边际总和法是把收益与损失相等时作为临界点，根据每一个影响因素分类的不同水平所计算的纯保费之和等于相应的赔付边际成本之和。假设影响因素分为2 类，费率计算公式为

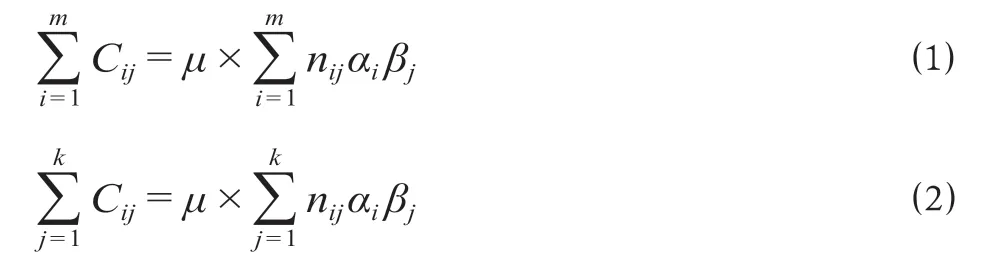
式中：Cij为每个类别的赔付边际成本；i为影响因素1 的分类；j为影响因素2 的分类；μ为整个影响因素集合的平均纯保费；nij为每个类别的单位数；αi，βj分别为每类影响因素的相对费率。

由公式(1)可得相对费率计算公式，即目标函数为

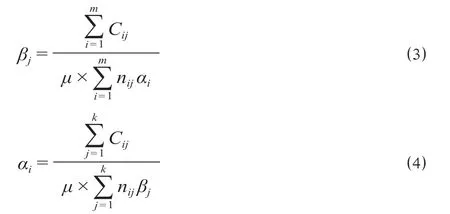
令分类变量αi的相对费率为1，即α1=α2= …=αm= 1，将其带入βj的计算公式，计算得到的βj代入αi的计算公式，通过不断迭代可以得到收敛的相对费率值，根据结果值进行回归计算得到相应的纯保费。

1.2 经典费率计算方法

广义线性模型计算方法采用的经典费率计算方法是传统线性模型的扩展，常见的有正态分布、泊松分布、伽马分布和逆高斯分布等方法，通过联结函数建立响应变量的数学期望值与因素变量之间的关系[2-4]。假设r维的响应变量Y服从指数型分布，概率密度函数可以表示为

式中：yp为响应变量，f(yp|θp，ω)为对应的概率密度函数，p= 1，2，…，r；θp为自然参数；ω为离散参数；b(θp)，c(yp，ω)为相应指数分布的已知函数。

假设1：因素变量可以表示为线性组合

式中：ηp为线性向量模型；xp为对应于yp的q维自变量X(即因素变量)的观测值；β为q维未知参数。

假设2：yp的均值μp与ηp关系式可以表示为

式中：g(μp)为联结函数。

1.3 费率计算方法比较

广义线性模型计算方法与传统费率计算方法相比较具有以下优势。

（1）分布更加灵活。传统费率计算方法通过加法或者乘法进行费率迭代计算，而广义线性模型的计算方法是将各费率相加后通过联结函数进行变换处理，广义线性模型允许因素变量服从更为广泛的分布族，即线性指数分布族，与普通的线性回归模型比较，具有更大的灵活性。

（2）计算更加高效。虽然传统费率计算方法原理简单，但风险因素较多时迭代公式比较复杂，计算量会非常大，而广义线性模型计算方法可以在很大程度上降低计算量。

（3）统计更加完整。传统费率迭代的计算方法不足之处是不能对计算结果进行严格的统计检验，而广义线性模型计算方法具有完整的统计检验模型。

在非寿险纯保费计算的应用中，更多地采用广义线性模型计算方法[5]，广义线性模型计算方法已经成为个人车险、其他个险、以及部分商险计算的指导性方法[6]，鉴于广义线性模型计算方法的优点，因而在退票险计算过程中采用广义线性模型计算方法。

1.4 计算方法检验指标

使用广义线性模型的方法计算退票险费率后，通过赤池信息量准则(Akaike Information Criterion，AIC)值和离差平方和指标进行计算方法的有效性检验。

（1）AIC。AIC 是衡量统计模型拟合优良性的一种标准，值越低表示拟合效果越好[7]。为防止过拟合，在评价模型时不能仅以拟合精度进行衡量，应是拟合精度和未知参数个数的综合最优化配置。

（2）离差平方和。离差平方和通常作为表征数据“离散程度”的指标，值越低表示拟合效果越好，计算公式为

式中：U为离差平方和；d为每个数据；v为所有数据的均值。

2 铁路退票险费率计算模型构建

2.1 模型构建

铁路退票险业务由费率计算模型、交易数据和盈亏评价模型组成，退票险业务交易数据变化与铁路退票险费率计算模型密切相关。退票险费率计算是费率计算模型的核心，主要依据历史交易数据形成退票险知识库信息，在售票和退票业务办理过程中对退票险知识库信息进行应用，并产生新的交易数据。铁路退票险费率计算模型由影响因素识别、费率计算和退票险知识库闭环管理组成。铁路退票险费率计算模型如图1 所示。

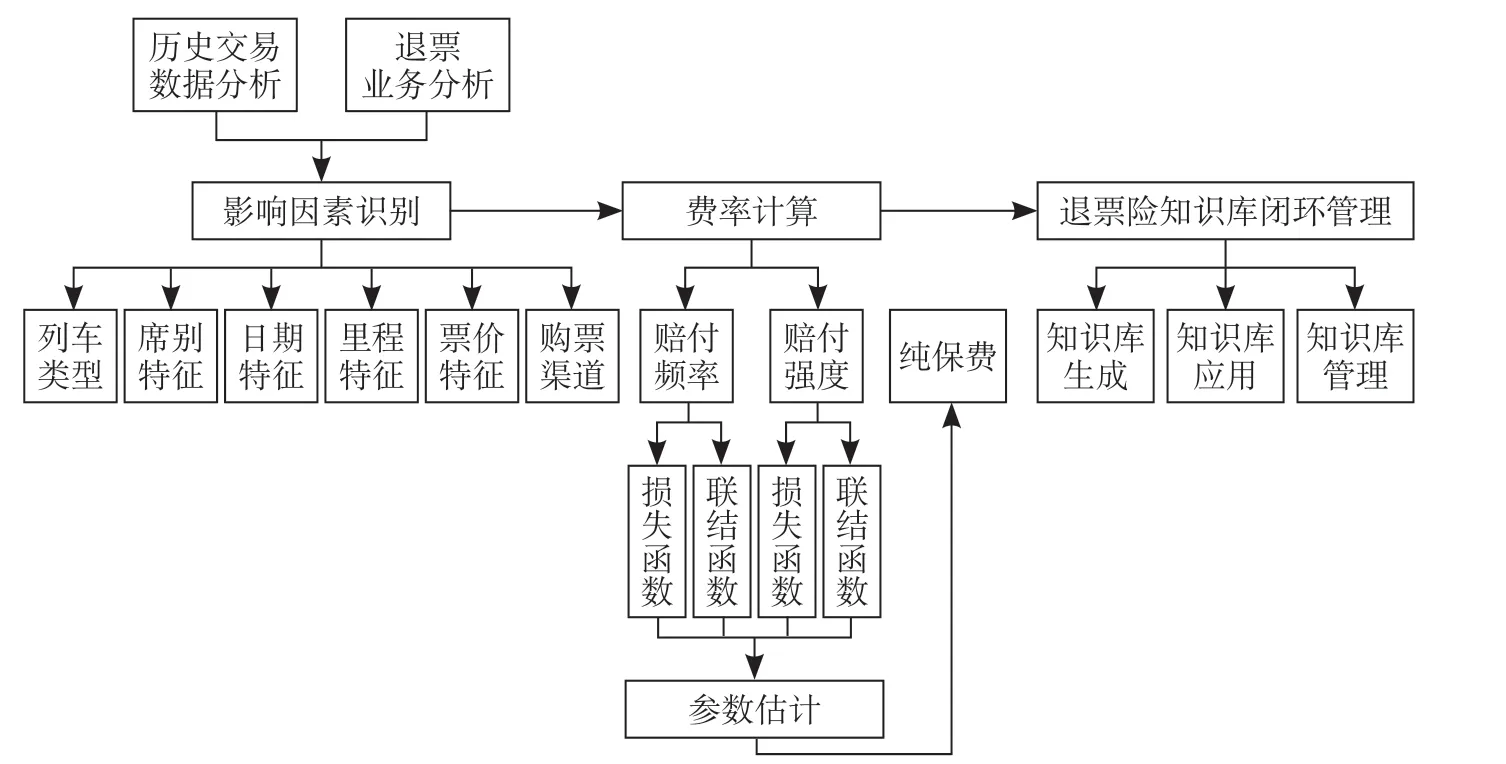
图1 铁路退票险费率计算模型Fig.1 Rates model of railway refund insurance

2.2 影响因素识别

首先需要依据风险因素进行分类，从而确定分类风险变量[8-10]，将影响因素的属性值作为后续费率计算的自变量。可以通过分析铁路售票、退票、有退票险的退票费赔付等数据，识别铁路退票险影响因素。铁路退票的发生，排除自然或者列车调图等原因外，主要为旅客行为。其中，由于自然灾害或者运行图调整等铁路责任，所发生的退票一般不收取退票费，不存在赔付；旅客行为从舒适程度、经济压力和便捷程度等方面考虑赔付。

（1）舒适程度。旅客舒适度受到列车类型、席别、里程和乘车日期影响，旅行历时越短，席别等级越高，人员拥挤度越低，则旅客舒适度越高。列车类型为目前旅客群体客座率较高的高速铁路列车、动车组列车和普速铁路列车；席别特征包含列车类型对应的所有席别种类；日期特征根据既有的假期进行分类；里程特征以1 000 km 为节点进行里程归属分类。

（2）经济压力。所购买车票的票价越低，旅客所承担的经济压力越小。票价特征以300 元为节点进行票价分类。

（3）便捷程度。购票渠道包含既有的互联网、手机APP、车站窗口、代售点窗口、TVM 和电话订票渠道。通过手机APP 退票比其他渠道便捷，在开车前可以随时随地办理退票手续。而且已经注册12306 账户的乘车人不论通过哪个渠道购买电子客票，均可以通过手机App 或者互联网渠道办理退票。

当票价相差不大时，旅客会优先考虑舒适度高、发车日期，以及发点最优的列车，然而一旦有更适合的车票，次优车票被退票的可能性将提高，而且便捷的退票渠道也将提高退票的概率。综上，退票险影响因素包括列车类型、席别特征、日期特征、里程特征、票价特征和购票渠道，退票险影响因素如表1 所示。

2.3 费率计算

退票险费率是退票险保费计算的依据，通过对非寿险费率计算方法的比较分析，选择广义线性模型的方法进行退票险费率计算。进行退票险费率计算之前，首先应明晰以下几个变量的含义。一是风险单位，风险度量的基本单位，是保险标的发生1 次风险可能造成的最大损失范围，如车辆险以1 辆汽车为1 个风险单位；二是赔付频率，一定时期内每个风险单位的赔付次数，描述风险发生的可能性，通常用赔付总次数和风险单位数的比值进行估计；三是赔付强度，1 个风险单位每次赔付的金额，描述风险发生的严重程度，通常用赔付总金额与赔付总次数的比值进行估计。

按照风险单位的含义，对于退票险，1 张车票即为1 个风险单位，1 张车票只能退1 次，赔付频率为1 或者0，赔付强度为车票的退票损失补偿金额。为研究风险类别对应的保费，形成费率体系，以退票险影响因素“列车类型、席别特征、日期特征、里程特征、票价特征和购票渠道”为风险类别，研究一定时期内每个风险类别的赔付频率及赔付强度。风险单位数为购买退票险的每个风险类别的车票总张数；赔付总次数为每个风险类别实际进行赔付的总次数，即按照风险类别产生的退票损失补偿总次数；赔付总金额为每个风险类别实际进行赔付的总金额，即按照风险类别产生的退票损失补偿款之和。因此，按照风险类别的赔付频率和赔付强度计算式分别为

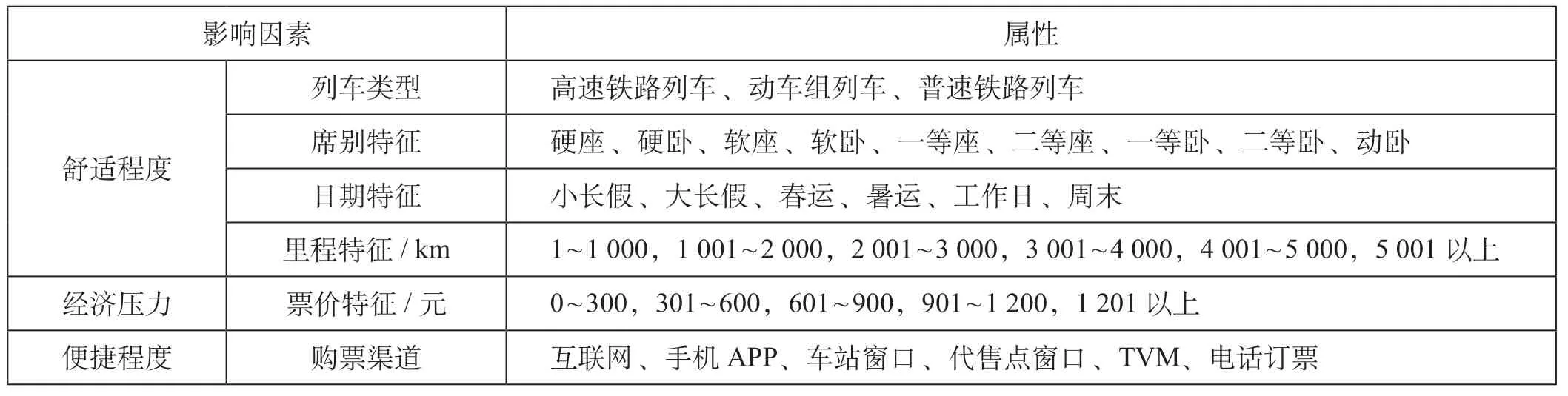
表1 退票险影响因素Tab.1 Influencing factors of refund insurance

式中：Lcp为按照风险类别的赔付频率；Lcn为按照风险类别的退票损失补偿总次数；Ts为按照风险类别的购买退票险的车票总张数；Lca为按照风险类别的赔付强度；Mc为按照风险类别的退票损失补偿总金额。

目前铁路退票时实行“梯次退票”规定，旅客退票费不再按固定比例收取，而是分别按票价的5%，10%和20%来收取。在距离发车不同的时间阶梯内，退票费率不同，旅客越早退票，收取的退票费就越低。退票险购买的初衷是转移退票风险，补偿退票费损失部分，由于旅客是否退票的原因具有复杂性、客观性，每一位旅客对于退票风险的预估是不同的，一般会在行程不确定、购买的车票不是理想车票等情况下购买退票险。现在铁路还没有开展退票险业务，暂时没有退票险购买及退票后的赔付数据，因而在进行费率计算前，假设：每笔退票都已经购买退票险；收取退票费的退票均已经进行赔付。在该假设条件下进行费率计算，未来实施退票险后，购买退票险的车票不一定发生退票，进行退票的车票不一定已经购买退票险，对费率计算模型评价后，如果需要优化费率体系则根据实际的购买及赔付数据进行费率计算。

2.4 退票险知识库闭环管理

根据费率计算的输出结果形成退票险费率体系，作为退票险知识库的重要组成部分。退票险知识库由退票险费率计算体系和退票损失补偿体系组成，为退票险业务应用提供依据，包括退票售保和赔付等的规则和基础信息，通过在售票和退票时进行知识库信息的应用，在交易数据产生后进行盈亏分析，对退票险费率计算模型进行评价，以改进费率计算部分并优化退票险知识库信息，形成对退票险知识库的闭环管理，退票险知识库闭环管理如图2 所示。

在退票险知识库中，将退票险费率计算得到的风险类别的纯保费和附加保费相加得到的保费作为基础数据。在预售期内购买车票时，旅客自愿选择是否购买退票险，当选择购买退票险时，根据所购车票信息从退票险知识库获得对应风险类别的退票险费用信息。如果已经购买退票险，一旦发生退票时，根据退票险知识库的损失补偿体系采用即时或者事后方式进行净退款计算，并进行退票存根及赔付存根的关联信息记录。即时赔付是将赔付费用与退票费用一并计算，退票完成时赔付即完成，如可以按照目前的阶梯退票费率，购买退票险的旅客将执行降级一档，或者计算退票费率时，距离开车时间自动加1 d 来承担部分损失，获得赔付后的净退款。事后赔付是在不影响目前的退票业务的前提下，退票完成后，在一定工作日内将赔付费用返回到旅客账户。赔付方式需要根据历史退票及赔付数据进行分析后制定，并根据铁路退票险盈亏评价模型进行退票险知识库信息的优化。

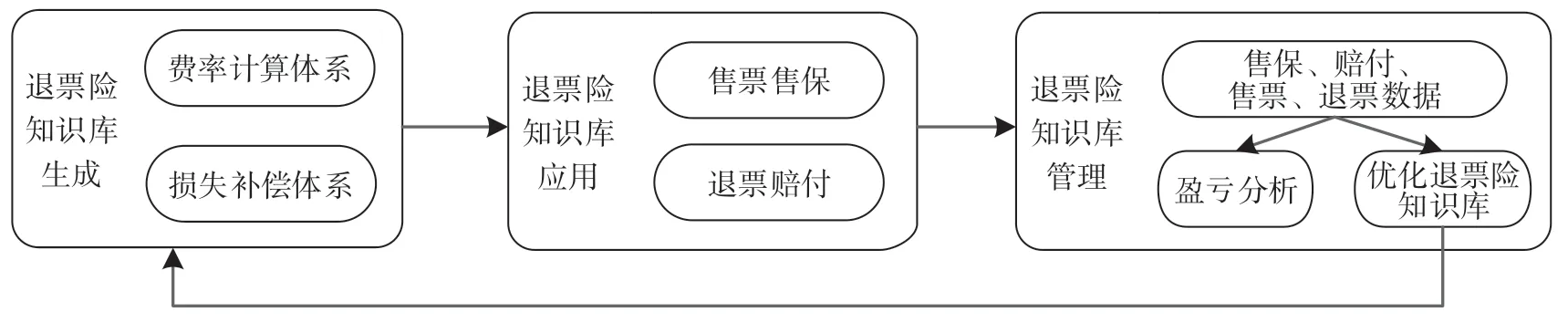
图2 退票险知识库闭环管理Fig.2 Closed loop management of refund insurance knowledge base

3 案例分析

3.1 铁路退票险费率计算

通过使用广义线性模型的方法计算铁路退票险费率，根据业务的先验信息选择合适的损失概率密度函数及联结函数，进行赔付频率和赔付强度的参数估计，并利用参数的估计值进行回归计算后得到纯保费。

（1）选择损失概率密度函数及联结函数。选取2017 年、2018 年某线路列车退票数据，依据已识别的退票险影响因素对实验数据进行预处理，将实验数据按照影响因素的属性值进行归类统计，依据公式(11)和公式(12)生成退票险风险类别对应的风险单位数、赔付总次数、赔付总金额等数据，用以进行赔付频率及赔付强度分布的研究，研究中对客票数据进行脱敏处理。赔付频率实验数据呈左偏趋势，赔付强度实验数据呈右偏趋势，截去赔付频率小于0.4 的样本数据和赔付强度右偏并且强度极大而且个数极少的样本数据后，赔付频率及赔付强度的密度分布如图3 所示。根据其他行业对保费的既有研究及铁路退票按风险类别的赔付频率、赔付强度数据的分布情况，分别选择泊松分布、正态分布作为赔付频率的损失分布函数，分别选择伽玛分布、正态分布作为赔付强度的损失分布函数，其中自变量为xpq(p= 1，2，…，6；q= 1，2，…，c，c为xp的属性个数)。为确保退票险的相对费率之间是相乘关系，选择对数联结函数。

（2）参数估计。参数估计结果如表2 所示。表2 为赔付频率和赔付强度分别采用不同的损失概率密度函数建立广义线性模型时得到的参数估计结果。根据本次实验数据，自变量“里程特征”仅使用x41和x42类，其它自变量为表1 中的所有分类。通过显著性检验分析，赔付频率的损失概率密度函数选择泊松分布，赔付强度的损失概率密度函数选择伽马分布。

（3）纯保费计算。首先得到各风险分类的赔付强度和赔付频率的期望值，通过赔付频率和赔付强度期望值的乘积计算该风险类别的铁路退票险纯保费。当退票险试行后，购买退票险的车票不一定发生退票，退票后不一定发生索赔，根据对费率计算模型的评价结果，基于历史退票数据及保险数据可以采用同样的方法建立赔付频率和赔付强度模型。

3.2 有效性验证

（1）退票险赔付频率和赔付强度的有效性验证。使用2019 年同一线路列车的数据给出赔付频率、赔付强度的验证结果，包括离差平方和、AIC值。其中，计算赔付频率的离散平方和时，“每个数据”指每个赔付频率值，均值为赔付频率的均值；计算赔付强度的离散平方和时，“每个数据”指每个赔付强度值，均值为赔付强度的均值。赔付频率及赔付强度拟合优度比较如表3 所示。从表3检验结果可知，对于泊松分布来说，其离差平方和低于正态分布，说明泊松分布对于样本数据拟合效果优于正态分布；另外，在使用赤池信息量准则进行检验时，泊松分布的AIC 值较低，说明其在拟合精度和复杂度之间的平衡关系做的更好。同样，从表3 检验结果可知，赔付强度采用伽玛分布拟合优度优于正态分布。

（2）退票险纯保费的有效性验证。用传统的迭代法与广义线性模型的方法进行比较验证。采用差值比对有效性进行验证，差值比D计算式为

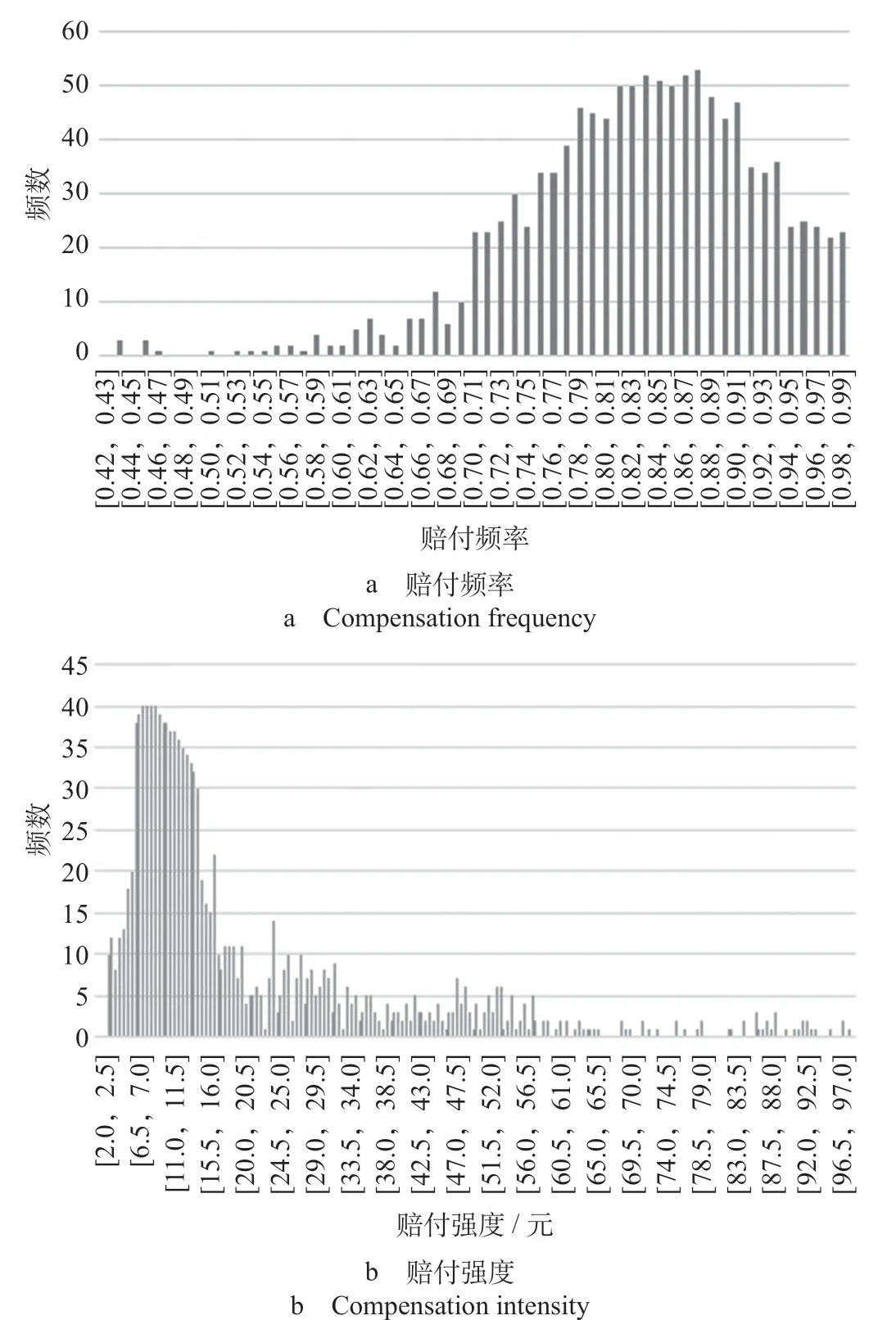
图3 赔付频率及赔付强度的密度分布Fig.3 Density distribution of compensation frequency and compensation intensity

式中：IGLM为退票险费率计算模型计算的纯保费；Iite为迭代法计算的纯保费。

以2017 年、2018 年同一线路列车样本数据为数据源，采用基于广义线性模型的方法进行纯保费计算后，与对应各退票险风险类别的迭代法纯保费进行比较，退票纯保费有效性验证如图4 所示。其中横坐标为退票险风险因素的各种分类类别，如“高速铁路列车/一等座/春运/1 ～1 000 km/0 ～ 300 元/互联网购票”、“高速铁路列车/ 一等座/ 春运/1 001 ～ 2 000 km/301 ～ 600 元/互联网购票”等。

从图4 可以得出基于目前的实验数据，除个别高额票价的类别外，差值比基本在[-0.1，0.1]之间，客票票价目前都是以元或者0.5 元为单位，在纯保费计算时同样以此为单位，因而差值为1 元或者0.5元是合理的，2 种方法计算的纯保费差别不大。在实验中传统迭代法采用边际总和法，迭代法的原理简单，但是风险因素较多时迭代公式复杂，计算量非常大，效率较低。用广义线性模型的方法比边际总和法节省3 倍左右时间，因而依据广义线性模型方法计算退票险费率合理有效。

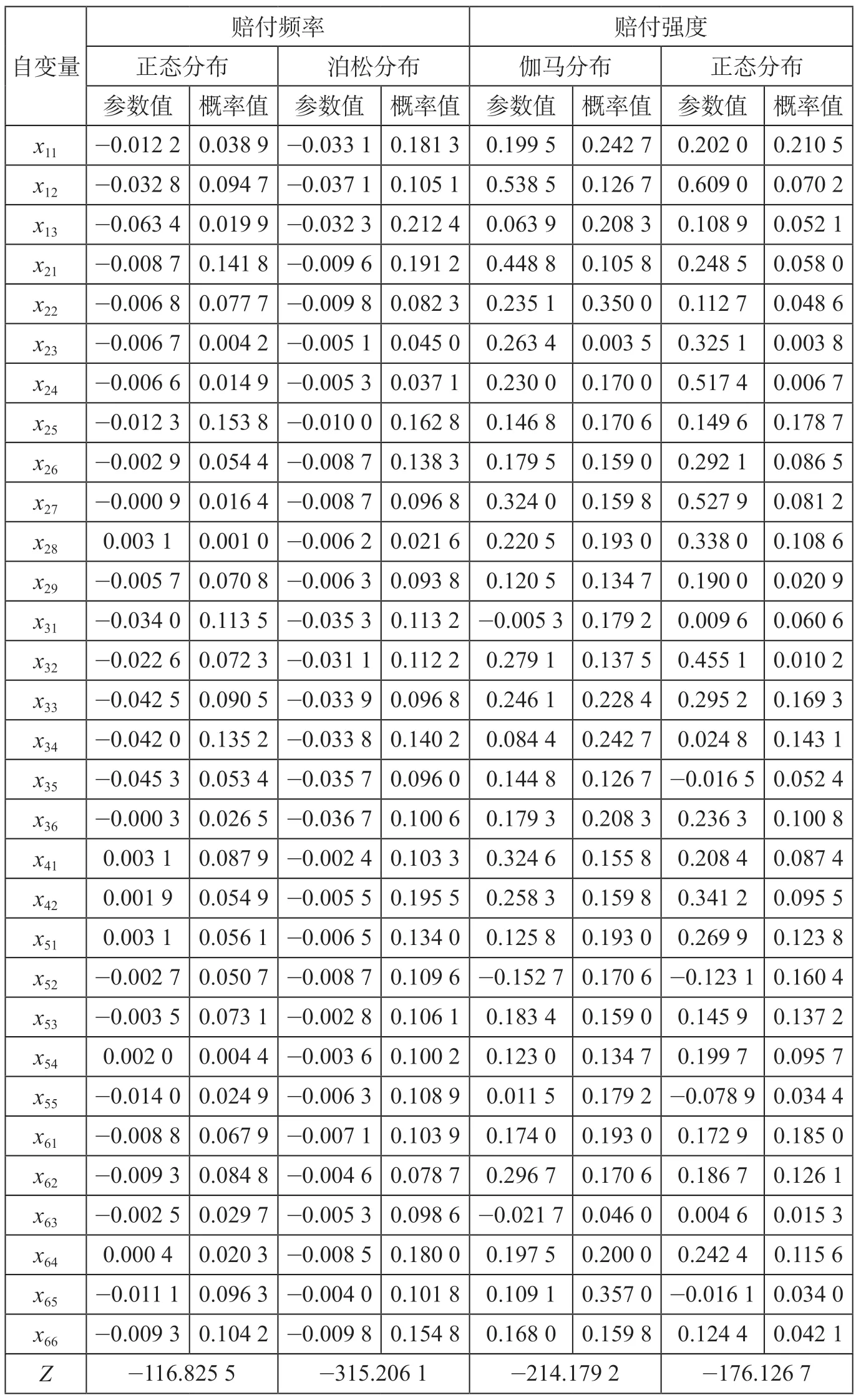
表2 参数估计结果Tab.2 Result of parameters estimation

表3 赔付频率及赔付强度拟合优度比较Tab.3 Comparison on the fit goodness of compensation frequency and compensation intensity

4 结束语

随着高速铁路的快速发展，旅客的出行越来越便利，由于出行前突发情况的难预测性，旅客需要为无法出行的退票行为承担经济损失，退票险的推进可以转移由于退票行为产生的经济损失的风险。制定退票险费率是退票险业务应用的基础，结合铁路旅客退票行为的实际和特点，研究铁路退票险费率计算模型，有助于加快铁路退票险费率出台。退票险费率是退票险保费计算的依据，购买退票险后，发生退票时需要按照规则进行赔付，因而还应研究退票损失补偿体系，构建全面的退票险体系。

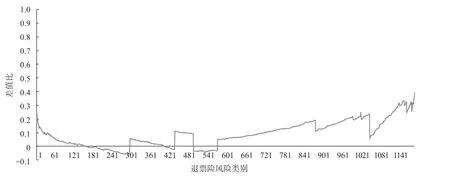
图4 退票纯保费有效性验证Fig.4 Validity verification of pure premium on refund