Constructing refined null models for statistical analysis of signed networks∗
Ai-Wen Li(李艾纹), Jing Xiao(肖婧), and Xiao-Ke Xu(许小可)
College of Information and Communication Engineering,Dalian Minzu University,Dalian 116600,China
Keywords: signed networks,null models,statistical analysis,average degree connectivity,embeddedness
1. Introduction
Signed social networks are a special type of social network with two types of relations,including positive edges such as“friends”and“trust”,and negative edges such as“enemies”and“distrust”.[1,2]The particularity of signed networks is that its topology emergence is partly determined by the correlation between positive and negative edges.[3-5]The existence of negative edges in signed networks challenges many statistical analysis methods in the field of complex networks.[6,7]For example, Cotti et al. calculated the classical average degree connectivity of positive and negative topologies respectively,but it is difficult to know how the signs of links between nodes affect the pattern of such correlations.[8]
In the processes of statistical analysis, to ensure the accuracy of experimental results,[9]a reasonable method is to first calculate the same statistic of a real-life network and its corresponding randomized version, and then to compare their values for revealing the nontrivial properties of signed networks.[10,11]The randomized networks with some of the same properties as a real-life network are called null models.[12,13]At present,there are two kinds of classical null models for signed networks: sign[14]and full-edge[15]randomized null models. The sign randomized null model guarantees that the signs of edges are randomized while keeping the position of each edge fixed. The full-edge randomized null model shuffles both the signs and the positions of edges at the same time.
However, people pay less attention to null models of signed networks. Only the above two null models have been used in the previous studies of signed networks.[16,17]In signed networks and other types of online social networks, studies on the generating mechanism of social networks should refer to appropriate null models.[18,19]When studying some statistical properties of signed networks, due to the existence of negative edges, the general null models shuffling both positive and negative topologies simultaneously cannot consider the effect of positive edges, negative edges,and the correlation between them on network statistical properties. Therefore, it is necessary to reconstruct more refined null models for signed networks to understand the complex structural properties of signed networks.
To solve this problem, we constructed more refined null models by randomizing three kinds of edges: positive edges,negative edges, positive and negative edges, respectively. In the experiments of real-life signed networks,we compared two classical null models and three new ones on various statistical indicators. The results show that the proposed null models can more efficiently reveal the roles of positive edges,negative edges, and the correlation between them in signed networks,which are different from two classical ones. The results indicate the position of positive edges has a stronger effect on positive-edge topology,while the signs of negative edges have a greater influence on negative-edge topology. For some specific statistics (e.g., embeddedness), the results indicate that the proposed null models can more accurately describe reallife networks and are helpful in providing different reference models for statistical analysis of signed network topologies.Our models take into account the interaction of two kinds of edges,and the significance of negative edges can be correctly analyzed to understand the complex structural properties generated by the original real-life networks.
2. Description of empirical network data
In this study, we use the following real-life signed networks: bitcoinalpha, wiki-RfA, epinions and slashdot, which can be obtained from the Stanford Network Analysis Project(SNAP) website.[20]It should be noted that we only use the sign information of empirical signed networks to build undirected signed networks, ignoring the weight and direction of each edge.
Bitcoinalpha is a trust network of people who trade bitcoin on the platform called bitcoin alpha.[6]Bitcoin users are anonymous, so it is necessary to maintain user reputation records in order to prevent transactions with fraudulent and risky users. Users of these platforms rate other users in a scale of −10 (total distrust) to +10 (total trust) in steps of 1. The sign of a user’s rating for another user is the sign of the edge formed by two connected users. The network consists of 3783 nodes and 14124 edges, among which 12759 edges are positive accounting for 90.3% and 1365 edges are negative accounting for 9.7%.
Wiki-RfA is a network of voting between wikipedia members. To make a wikipedia editor to be an administrator,a candidate or another community member must submit a Request for Adminship (RfA).[21]Subsequently, any wikipedia member can vote for support, neutrality, or opposition. The nodes of this network represent these members,and the positive and negative edges represent the votes supported and opposed,respectively. The network consists of 10835 nodes and 171800 edges,among which 132954 edges are positive edges accounting for 77.4%and 38,846 edges are negative edges accounting for 22.6%.
Epinions is a who-trust-whom online social network of a general consumer review site epinions.[7]Registered users of epinions can declare their trust or distrust toward one another,based on the comments they post. The trust relationship between a pair of users represents a positive edge. Conversely,the distrust relationship between a pair of users represents a negative edge. The network consists of 131828 nodes and 711783 edges, among which 592551 edges are positive accounting for 83.2%and 119232 edges are negative accounting for 16.8%.
Slashdot is a network formed by users tagging each other as friends or enemies on the website called slashdot(www.slashdot.org),which is a technology-related news website known for its specific user community.[7]This network was obtained in February 2009 in which nodes represent users,and the positive/negative edges represent friends/enemies.The network consists of 82144 nodes and 500481 edges, among which 381648 edges are positive edges accounting for 76.3%and 118833 edges are negative edges accounting for 23.7%.
3. Null models of signed networks
In the field of network science, a null model is the randomized network with some of the same properties as a reallife network. When ensuring the same number of nodes as the original network, different levels of null models can be constructed according to a series of coarse to refined constraints.[22]The 0 K null model only guarantees the same average degree as the original network, leading to the strong randomness for network topology and making it seldom used in practice. The 1 K null model with the same degree distribution as the original network is usually used. In the studies of signed networks,sign-randomized,and full-edge-randomized are two commonly constructing methods for the 1 K null model.
The sign randomized null model is constructed by randomizing the signs of edges while keeping the position of each edge fixed. The one-step constructing process is shown in Figs. 1(a) and 1(b). After randomly selecting positive edge BC and negative edge DE, and then exchanging their signs in Fig.1(a), the sign randomized null model is generated as shown in Fig.1(b). The full-edge randomized null model is constructed by randomizing all the edges, where both the signs and positions of edges are randomized. The one-step constructing process is shown in Figs. 1(a) and 1(c). Randomly disconnect positive edge BC and negative edge DE in Fig.1(a),then connect nodes B and D,C and E to form edges BD and CE,respectively. During the exchange,if we keep the signs on two edges BD and CE consistent with BC and DE,the full-edge randomized null model is generated as shown in Fig.1(c).
Because randomizing signs or full-edges do not guarantee that the number of positive and negative edges of each node(i.e., {k+(i)} and {k−(i)}) remain unchanged before and after randomization, the topology correlation between positive and negative edges may vary when constructing the two null models. Actually, they can only guarantee that the following degree sequence{k+(i)+k−(i)}is the same as that of the original network. In order to investigate the correlation effect between positive and negative edges on network property,we construct three refined edge-randomized null models with less randomization: positive-edge randomized, negative-edge randomized,positive-edge and negative-edge randomized,respectively. They can keep the two degree sequences({k+(i)}and {k−(i)}) the same as the original network, so they retain more structural characteristics than sign and full-edge randomized null models. The inclusiveness among the five null models is shown in Fig.2.

Fig.1. The constructing process of five null networks. (a) The original toy network, which has 4 positive edges (i.e. AB, BC, DF, and EF), and 3 negative edges (i.e. AC,CD, and DE), (b) sign randomized null model,(c) full-edge randomized null model, (d) positive-edge randomized null model,(e)negative-edge randomized null model,and(f)both positive-edge and negative-edge randomized null model.

Fig.2. The inclusiveness among different signed null models.
If we disconnect positive edges BC and DF in Fig.1(a)and then connect nodes B and D, C and F to form two new positive edges BD and CF, respectively, the positive-edge randomized null model is generated as shown in Fig.1(d).This process just randomizes the positive edge topology while keeping the negative topology intact. Similarly, the negative-edge randomized null model is generated as shown in Fig.1(e). It just randomizes the negative topology while keeping the positive topology intact. Besides,to study the superposition and correlation of positive and negative topologies, we also construct the positive-edge and negative-edge randomized null model,as shown in Figs.1(a)and 1(f). It should be noted that this null model in Fig.1(f) guarantees that only positive(negative)edges shuffle each other,which is different from the full-edge randomized model that the shuffling operation can take place between positive and negative edges in Fig.1(c).
We only show how to do one-step randomization of each null model in Fig.1. In a large-scale empirical network, the above construction process needs to operate many times before a stable random network can be obtained. The algorithm process of the positive-edge randomized null model show as algorithm 1. The algorithm of negative-edge randomized null models has a similar process,only in step 3 the conditions become negative edges. The algorithm process of positive-edge and negative-edge randomized null model is to execute algorithm 1 first and then the algorithm of negative-edge randomized null models. Our experimental experience finds when the number of rewired edges reaches twice the number of edges,the structural characteristics of the null network no longer strongly changes as the number of rewired edges increases,indicating that the original network has been sufficiently randomized. In this study,all the statistical results of null models are calculated under this condition.
Algorithm 1The positive-edge randomized null model.
Input:The original network, randomize times, maximum number of tries
Output:The network after randomizing the positive edges
1: -Select two different nodes from the network, U and X,respectively
2: -Select a node V from all nodes connected to node U and a node Y from all nodes connected to node X
3: -If V /=Y and UV and XY are both positive edges, add UX and VY edges to the network and remove UV and XY from the network
4: UNTIL(termination criterion is met)
5: Output the randomized network
4. Statistical analysis of signed networks based on null models
A signed network includes the collective topology with positive and negative edges,and the whole network also can be divided as a positive subnetwork and a negative subnetwork.To measure the complicated topology characteristics of a reallife signed network,statistical indicators such as clustering coefficient, average degree connectivity, and embeddedness are calculated as follows.
4.1. Clustering coefficient
The clustering coefficient characterizes the tendency of nodes in a network to form small clusters (i.e., triangle structure).[23,24]It is defined as the ratio of the actual number of triangles containing node i to the total number of triangles that node i may form. The equation of cluster coefficient Ciof node i is as follows:

where lirepresents the number of edges between neighbor nodes of node i and kiis the number of neighbors of node i,namely,the degree of node i. The average clustering coefficient of all the nodes is defined as follows:

where N is the total number of nodes. The range of C is from 0 to 1. The closer C is to 0, the weaker clustering of the network is. Conversely the closer C is to 1, the stronger it is.When C=1,it means that the network is global coupling. In other words, any two nodes are connected to each other. In a signed network,the C values of positive subnetwork(i.e.,C+)and negative subnetwork (i.e., C−) can be calculated respectively. Besides, for the whole signed network with positive and negative edges,the signed clustering coefficient Cscan be defined algebraically using network adjacency matrix,[2]and the equation is as
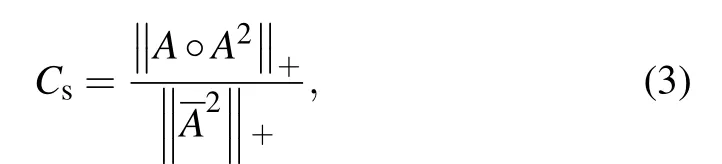
where A is the symmetric adjacency matrix of the sign network, which contains the value of −1 for a negative edge,A is a unsigned symmetric matrix with a diagonal of zero,A◦B represents the Hadamard product (entrywise product) of two matrices,and‖A‖+denotes the sum of all the elements in matrix A. The range of the signed clustering coefficient is from−1 to 1. In real-life social networks,the value of Csis usually positive.[2]

Table 1. The clustering coefficients of positive, negative, and the whole network, including bitcoinalpha and wiki-RfA, compared with the five kinds of null models. Bitcoinalpha(+)or wiki-RfA(+)represents the subnetwork of the positive edges in network,bitcoinalpha(-)or wiki-RfA(-)represents the subnetwork of the negative edges in network, and bitcoinalpha or wiki-RfA represents the collective topology with positive and negative edges of network. C, C+, C−, and Cs represents the statistic of clustering coefficient, the clustering coefficient of the positive-edge subnetwork, the clustering coefficient of the negative-edge subnetwork, and the signed clustering coefficient of the whole network. “original”,“sign”, “full”, “positive”, “negative” and ‘positive and negative” represents the original real-life network, the sign randomized null model, the full-edge randomized null model, the positive-edge randomized null model, the negative-edge randomized null model, and the positive-edge and negative-edge randomized null model. The abbreviations in Figs.3 and 4 are the same as in this table.
In the experiments of bitcoinalpha and wiki-RfA, the clustering coefficients of positive subnetworks (i.e., bitcoinalpha(+) and wiki-RfA(+)), negative subnetwork (i.e.,bitcoinalpha(-)and wiki-RfA(-)),and whole bitcoinalpha and wiki-RfA network have been calculated, which are shown in Table 1. In the results of bitcoinalpha,the three results of null models closest to the values of the original network are highlighted in bold. For the bitcoinalpha(+)subnetwork,randomizing negative edges does not affect the connection relationship of positive edges, so the result of the negative-edge randomized null model is the same as the original one, and they are both 0.160. For the bitcoinalpha(-)subnetwork, randomizing positive edges does not affect the connection relationship of negative edges, so the result of the positive-edge randomized null model is the same as the original one, which is 0.036. For the whole bitcoinalpha network, because the ratio of negative edges only accounts for 9.7%, randomizing negative edges has less influence than that of positive edges on clustering coefficients. The result of the negative-edge randomized null model is closer to that of the original one(0.052 vs. 0.054). Similarly,there are similar results in wiki-RfA.It should be noted that the ratio of negative edges accounts for 22.6%, so the result of randomizing negative edges is quite different from the original network.
The above results indicate that randomizing different kinds of edges have diverse effects on network clustering coefficient. Randomizing positive(negative)edges only changes the properties of the positive (negative) topology. Compared with two classical null models (i.e., sign and full-edge randomized null models),the different effects of positive and negative edges on clustering coefficients can be clearly analyzed based on the three proposed null models. By comparing the full-edge randomized null model and the positive-edge and negative-edge randomized null model, the effect of the correlation between positive and negative edges on network statistical properties can be identified. As shown in Table 1, for the network of result of bitcoinalpha, because negative edges are more sparse than positive ones, the effect of the correlation between positive and negative edges is more obvious on C−(0.003 vs. 0.037),less so on C+(0.068 vs. 0.065)and Cs(0.030 vs. 0.032).
4.2. Average degree connectivity
The average degree connectivity Knn(k), namely, the average degree of the nearest neighbors of nodes with degree k, is one method of measuring degree correlation in complex networks.[25]It is defined as where the transitional probability p(k′|k)can be defined as the conditional probability that a link emanating from a node of degree k is connected to a node of degree k′. That is,


where 〈k〉 means the average degree of all the nodes, 〈k〉=∑kkp(k),and p(k)is defined as the probability that picking an arbitrary node of k degree,and p(k,k′)is the joint probability that a randomly chosen link connects two nodes of degrees k and k′. That is,

Substitute Eq.(6)into Eq.(5)and then into Eq.(4)to get

If Knn(k)is an increasing function of k on average,it indicates that high-degree nodes tend to connect to other high-degree nodes,which means the network is assortative and vice versa.If there are no degree correlations in a network, Knn(k) does not have a monotonic trend with respect to k.
To solve the problem that Knn(k) can only be used in unsigned networks, we calculate its corresponding values Knn(k+) of the positive-edge subnetworks (i.e., epinions(+)and slashdot(+)) and Knn(k−) of the negative-edge subnetworks (i.e., epinions(-) and slashdot(-)), respectively. Compared with the five kinds of null models,the results of positive and negative subnetworks for epinions and slashdot are shown in Fig.3. Notably, because randomizing negative edges does not change the positive topology, the result of Knn(k+) for the positive-edge randomized null model is the same as that of the original one, so we do not display it here. Moreover,for the positive subnetwork,Knn(k+)of the positive-edge and negative-edge randomized null model is the same as that of the positive-edge randomized null model,because the positive topology does not have any negative edges. The positive-edge randomized null model does not have any effect on the negative topology, so Knn(k−) of the negative-edge randomized null model is the same as that of the original network. For the negative subnetwork, the result of the positive-edge and negative-edge randomized null model is the same as that of the negative-edge randomized null model.

Fig.3. The values of Knn(k)in the real-life epinions and slashdot and theirs five null models. (a)The result of Knn(k+)for the positive-edge subnetwork epinions(+),(b)the result of Knn(k−)for the negative-edge subnetwork epinions(−),(c)the result of Knn(k+)for the positive-edge subnetwork slashdot(+),and(d)the result of Knn(k−)for the negative-edge subnetwork slashdot(−).
In Fig.3(a), Knn(k+) of the original network increases with the increase of k+and shows an assortative degree mixing pattern. The rising trend is also shown in the result of the sign randomized null model. However, Knn(k+) of full-edge randomized null model does not show a monotonic trend with k+, and it does not have obvious degree correlation pattern.Similarly, randomizing positive edges also does not have any pattern of degree correlation. The above results show that the connection relationship of positive edges has a greater influence on Knn(k+)compared with randomzing the signs of positive links. For Knn(k−)of the original negative subnetwork in Fig.3(b),it tends to decrease with k−increasing,which indicates a disassortative degree mixing pattern. For the sign and full-edge randomized null models, smaller Knn(k) is smaller than other null models and the results are parallel to the xaxis. They are very different from the original network due to the stronger randomness induced by breaking down the correlation between positive and negative edges. In contrast, although the negative-edge null model introduces the randomness of negative topology,it has little effect on negative topology because of the sparsity of negative edges in the real-life network. In addition,the above results follow a similar pattern to the influence of randomizing network topologies on clustering coefficients in Table 1. That is, for the positive topology,the effect of randomizing the signs of edges is small,but the effect of randomizing link relationships is large.For the negative topology, the opposite is true. This finding implies that positive edges have a stronger effect on the statistical properties of positive topology, while the signs of edges have a greater influence on negative topology. Similarly, in Figs. 3(c) and 3(d), different from two previous null models, the proposed null models show the unique trend. The sign and the full-edge randomized null models have shown more different statistics than that of the original network. It implies that positive and negative edges and their correlations have some influence on the networks. Besides, the null models proposed by us have less randomness than the previous two null models for signed networks. Under the condition of ensuring partial properties,the smaller randomization is,the better the validity of the null models is, so the null models proposed by us might be more useful than the previous two null models for signed networks.
4.3. Embeddedness
In a signed social network,the number of common neighbors between a pair of users is called the embeddedness indicator of them.[26]If two users have more common neighbors,they are more embedded. For the embeddedness of positive edges, the neighbor represents the common friend. At the same time, for the embeddedness of negative edges, the neighbor represents the common enemy. According to structural balance theory,[27]the more embedded two friends are,the higher probability where there is a positive edge between them is.On the contrary,the more embedded two enemies are,the lower probability where there is a positive edge between them is.[7]
In order to study the influence of positive and negative topologies on embeddedness,we calculate the fraction of positive edges between a pair of nodes in epinions comparing with those in its five null models. The experiment results are shown in Fig.4. It is found that the stronger the positive embeddedness (that is, the greater the number of common friends), the higher the fraction of positive edges between a pair of nodes in Fig.4(a). The results of sign and full-edge randomized null models are much lower than that of the original network.They are much less likely to have a positive edge between a pair of nodes under the same embeddedness. However, three new proposed null models have the same rising trend as that of the original one. Especially,the negative-edge randomized null model is the closest to that of the original network, and the positive-edge randomized null model is slightly lower than that of the original network. At last,the result of the positive and negative edges randomized null model is the lowest. The above results stand for the practical randomization ability of the five null models for the epinions network.

Fig.4. The embeddedness of positive edges and negative edges in epinions. (a)The result of positive embeddedness and(b)the result of negative embeddedness.
Moreover, the similar pattern can be found in Fig.4(b).The fraction of positive edges in the original network decreases as the number of common enemies increases, revealing that the strong embeddedness of negative topology harms the positive connection between nodes. In the sign and fulledge randomized null models, the fraction of positive edges is much higher than that of the original network and parallel to the x-axis. However, different from the two classical null models,the downward trend of three proposed ones are more obvious and similar to that of the original network. The difference between the two kinds of null models is that the classical two null model breaks the correlation of positive and negative edges,while the three proposed refined ones can maintain this embeddedness property.
5. Conclusion
In summary, by randomizing positive edges, negative edges, and these two edges, three refined edge-randomized null models for signed networks have been proposed. The experiments of real-life signed networks indicate that the proposed null models are more accurately for analyzing the nontrivial statistical properties of real-life network topologies compared to the classical null models,revealing the influence of positive and negative edges and the correlation between them. Our method is also helpful in providing different reference models for statistical analysis of signed network topologies. In this way,the nontrivial properties of signed networks can be accurately described so as to facilitate a better understanding of complex structures, functions, and dynamical behaviors on real-life signed networks.
Furthermore, the null models proposed by us have less randomness than the original two null models for signed networks. Our models are universal and applicable to any undirected signed network,such as online social networks,biological networks,and information networks. Unfortunately,there is a partial information loss when extending these models to directed networks.[28]In the future,we will extend these models to directed signed networks for further studying the effect of directional positive and negative edges on network topology.
- Chinese Physics B的其它文章
- Nonlocal advantage of quantum coherence in a dephasing channel with memory∗
- New DDSCR structure with high holding voltage for robust ESD applications∗
- Nonlinear photoncurrent in transition metal dichalcogenide with warping term under illuminating of light∗
- Modeling and analysis of car-following behavior considering backward-looking effect∗
- DFT study of solvation of Li+/Na+in fluoroethylene carbonate/vinylene carbonate/ethylene sulfite solvents for lithium/sodium-based battery∗
- Multi-layer structures including zigzag sculptured thin films for corrosion protection of AISI 304 stainless steel∗

