Estimation of biophysical properties of cell exposed to electric field
Hui Zhang(张辉), Liyang Wang(王李阳), Peijie Zhang(张培杰),Xiaodi Zhang(张小娣), and Jun Ma(马军)
1College of Physics&Electronic Engineering,Xianyang Normal University,Xianyang 712000,China
2College of Life Science,Shaanxi Normal University,Xi’an 710062,China
3School of Highway,Chang’an University,Xi’an 710064,China
4Department of Physics,Lanzhou University of Technology,Lanzhou 730050,China
Keywords: neuron,field energy,membrane deformation,ion concentration
1. Introduction
Distinct non-thermal biological effect of electromagnetic field on a biological system is independent of the thermal phenomenon. For neurons in the nervous system exposed to external electromagnetic field, the deformation of geometry occurs in the elastic media. And the distribution density of intracellular and extracellular ions concentration will be changed,because with polarization effect of electric field, ions can be propagated along the channels embedded into the membrane.From the cellular level,the relation between cell deformation and membrane potential,gradient distribution for ion concentrations can be estimated.[1]In fact, the release and activation of physiological and biochemical functions of the cell are much dependent on the channel current and distribution of intracellular and extracellular ion concentration. The propagation of ions in the cell and pumping across the membrane channels will change the membrane potential. Thus,different firing modes can be changed or selected. Considering its distinctive biophysical property with controllability, the vesicles model is often used to calculate the nonlinear response in biological tissue and cells. From the viewpoint of physics,shape deformation will change the capacitance of the media driven by external electric field. And thus the density of ions in the cell will be greatly changed. That is, the deformation of the lipid membrane and the changes of the intracellular and extracellular ion concentration can modulate the membrane potential. And firing modes in neural activities can be selected to probe membrane properties and to detect pathological changes in cells.[2-4]
In the last decades,many theoretical neuron models[5-10]have been proposed to estimate and predict the dynamics in electrical activities in biological neurons. Based on these neuron models, bifurcation analysis can be applied to mode selection and furthering synchronization control. Noise is often imposed on the nonlinear systems, so it can be detected by changing the noise intensity when the nonliner resonance occurs. On the other hand,nonlinear circuits are built and tamed to reproduce similar quiescent, spiking, bursting and chaotic oscillations in the sampled time series for detectable variable such as output voltage. If so,a feasible neural circuit[11-14]is obtained and more neural circuits can be connected to implement a functional neural network. In fact, for a feasible neuron model, the biophysical effect should be considered due completely to its complex anatomic structure and functional connection to astrocyte.[15-18]The occurrence of multiple and mixed modes[19-21]in neural activities results from the nonlinearity and high correlation between biophysical variables,therefore,electronic activities can be controlled to switch between different firing modes.A realistic biological neuron and smart neural circuit can perceive external stimuli in an intelligent way.In Refs.[22,23],a phototube is incorporated into the simple FHN neural circuit and its ability to encode external optical signals is realized.Furthermore,the thermistor is coupled with the FHN neural circuit. And the improved neuron can explain the dependence of firing modes on temperature,[24]which has distinct influence on the channel current across the thermistor in a branch circuit. In Ref. [25], the electric field variable is introduced into the Hindmarsh-Rose neuron model, and then the dynamics effect of external field on the media[26]is estimated. As is well known, the energy[27-29]plays an important role in keeping and regulating the mode selection in neural activities. And then energy pumping is calculated between two coupled biophysical neurons.[30]For extensive guidance, readers can find suggestions and comments in Refs.[17,31,32]and the references therein.
In a generic way, the effect of external electromagnetic field on the neuron and excitable media can be estimated by applying equivalent induction current to the known neuron models. Some intrinsic parameters can describe the physical properties of the cell and neurons, e.g., the capacitance of the elastic cell membrane. However,in a practical way,the cell shape will be changed in the presence of external electric field.Therefore,it is a challenge to calculate the changes of intracellular and extracellular ion concentration of cells,and further the fluctuation of membrane potential,energy release and pumping can be estimated when electric field is applied to the cell with different shapes. In the late 1950s,Schaw[33]began a series of studies of the influence of the electric field on biological cells,and proposed a simple spherical shell with given electric parameters. In the early 70s,Frieske and Mahning[34]and Helfrich[35]presented the elastic theory for lipid bilayers and estimated the effect of external field on phospholipid vesicle shape. In particular, the first experiment with phospholipid vesicle exposed to the electric field was verified in 1979,and it was found that the spherical vesicle changed into prolate vesicle.[36]Furthermore, electric fields[37]were used to investigate the deformation of a vesicle. It was found that the vesicle underwent a prolate-spherical-oblate shape change when the frequency of the applied field increased from 100 Hz to 100 MHz.[38]Extensive investigations have been carried out for estimating the cell deformation and mode selection in neural activities when alternating fields, pulsed, alternating current (AC) field and non-uniform field[39-44]were applied to the cells,respectively. Many theories about the mechanism of the cell deformation were proposed and explained,such as the small deformation theory combined with the Maxwell stress approach,[45]the minimization of the total free energy,[46,47]method of balancing the forces from electric, hydrodynamic,bending,and tension stresses exerted on the membrane,[48]the entropic and the enthalpic approach,[49]the two-dimensional boundary integral method.[50]These methods predicted the changes of the shape of vesicles with the frequency of applied electric field and the electrical parameter of vesicle medium.And most of these theoretical approaches and conclusions were consistent with the experimental results.
Except the confirmation of shape deformation of the cells induced by pressure from external electric field, the distinct pumping and propagation between the intracellular and extracellular ion concentration of the cell will have a great influence on the membrane potentials, which was clarified by the penetration theory of ions on the membrane, the theory of the ion cyclotron resonance of trans-membrane,[51]theoretical prediction for the effect of electromagnetic radiation ion concentration in cells.[52,53]A probability wave theory on the ion movement across cell membrane,[54,55]and the intercellular calcium oscillations synchronism modulated by ELF electromagnetic fields[56,57]were presented and discussed by the author of this paper. These previous researches are helpful to know the physical mechanism for propagation of ions driven by electric field. However,in these researches,seldom considered are the changes of ion concentration generated by the cell deformation. And the discussion about the field energy release in the cell is still kept open. Inspired by the previous researches finished by Hirpyuki,[37,45]we calculate the stored energy in cell membrane and investigate the propagation across cell membrane with appropriate geometric and dielectric parameters, meanwhile, we also estimate the critical frequency when the external electric field is used to generate distinct cell deformation.
2. Model and scheme
The biological cell contains a large number of calcium,potassium, sodium elements, with complex electromagnetic field formed inside and outside the cell. When the cell is exposed to external electric field, most of the ions are driven to change the spatial distribution density. And the membrane will be subjected to pressure when these ions are propagated across the membrane channels and pumped to the calcium pools. Therefore, with the field energy released, the shape of cell will be changed when ions are pumped out of the cell.That is, when the external electric field is imposed on the cell, the electromagnetic forces on all ions are converted into mechanic pressure on the membrane, which further triggers the cell shape change. The cell deformation is dependent on the physical property of external electric field and the media.Therefore,the electric energy stored in the cell membrane and the ion concentration on both side of the deformed cell membrane, are modulated to change the membrane potential into the one with appropriate firing modes. Based on the electromagnetic field theory,the energy pumping and release,balance of ion concentration across the membrane,and changes of the membrane voltage are discussed in single shell cell with different shape parameters.
The biological cell handled with a single-shell cell model[58]is shown in Fig.1. Due to complex interaction among ions, the biological cell in extracellular fluid will present a spherical shell shape covered by cell membrane,which separates the endoplasm from the extracellular fluid completely.
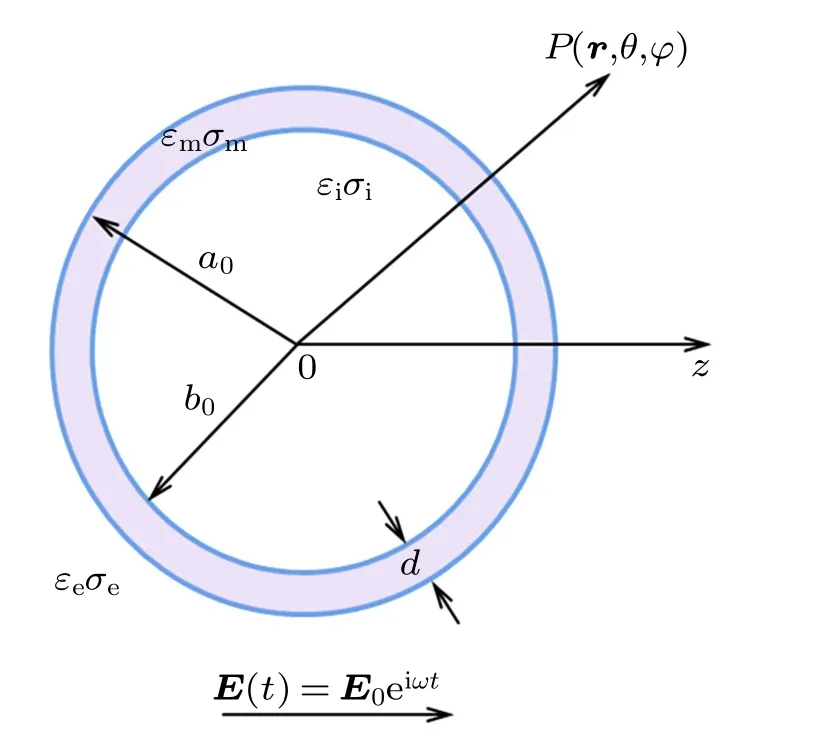
Fig.1. A single shell cell model, where a0 and b0 represent outer and inner radius of cell membrane,respectively,d denotes thickness of cell membrane,εi and εe refer to dielectric constant of the inside medium and outside medium,and σi and σe are conductivity for the media,and σm and εm are conductivity and dielectric constant for the membrane.
All these parameters are set to be constants throughout the following discussion. In the spherical coordinate system(r,θ,ϕ), θ is the polar angle, r is the victor for the position,and ϕ is the azimuth angle. The external electric field applied to the cell along the z axis is described by E(t)=E0exp(iωt).The boundary condition is defined before handling the cell deformation and potential distribution for the cell.For simplicity,the membrane,the inner and outer areas of the cell membrane are respectively labeled with subscripts m, i, and e. And the electric potentials of the corresponding areas are denoted as Ψm,Ψi,and Ψe,and the operator[45]is defined as follows:

According to the theory of biological electromagnetic field,the potential in the solving area satisfies the following criterion:Supposing that there is no local charge in the medium, while the potential inside and outside the cell membrane are


The physical condition requires

where raand rbrepresent the locations of the outer and inner surface of the cell membrane respectively,Ejn(j=i,m,e)denotes the normal component of the electric field Ejat the interface for the cell and medium. With the external field fixed in the z direction, the spatial distribution of potential is axisymmetric around the z axis.
As a consequence, the spatial distribution of electric potential ψe(r,θ), ψi(r,θ), and Δψ(θ) in the outer spaces, the inter spaces and the transmembrane potential can be estimated from

In addition,the coefficients A and D are respectively approximated by

The electromagnetic forces generated by the applied field can induce the deformation in the cell shape. The outer and inner surface of the deformation in the cell membrane are expressed in polar coordinates as follows:

where the function p2(cosθ) dependent on polar angle θ is defined in Legendre polynomials type, and g2represents the coefficient. The elongation modulus k is defined by
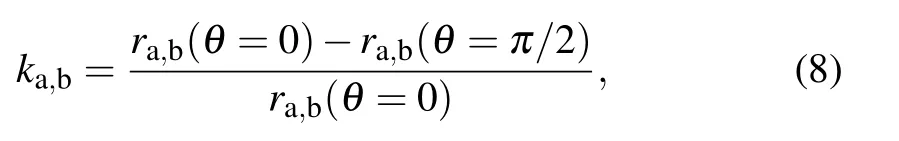
where ra,b(θ) is the measure of the position of outer surface ra(θ)and inner surface rb(θ)at a certain polar angle θ. When the applied field is weak and the shape deformation is slight,g2p2(cosθ) shows a lower-order perturbation. Considering the homogeneous and uniform case,the dielectric constant of the membrane is independent of the frequency of external electric field. The relationship between the elongation modulus and the frequency of applied field is given by

Here,the constant k0is the elongation modulus at f =0,and τ is the characteristic response time of the membrane to the external electric field. To further estimate the deformation effect induced by static/constant electric field, standard scale transformation is applied. And κ is defined as the elastic modulus of curvature on the surface of cell membrane. These intrinsic parameters are updated as follows:

According to the definition of ka,bin Eqs.(8)and(9),the obtained frequency fcunder k(fc)=0 is the critical transformation frequency between the prolate and the oblate shape in the cell. The value of fcis estimated from

A living cell often contains a large number of ions of several kinds,which can keep field energy.A generic capacitor is usually made of two conductors separated by vacuum or an insulating material,and it is normally used as a functional component because charges and field energy can be stored. In fact,the cell membrane can also be considered as a smart capacitor.And the field energy is pumped and released when the spatial distributions of ions are changed. In a local area with a finite size,the endomembrane and outer membrane can be approximated as a parallel-plate capacitor with a certain spacing(e.g.,the membrane thickness)in between.For simplicity,the membrane thickness of the isolated shell cell is denoted as d0and the capacitance density C0in the absence of cell deformation,and then the field energy density W0,which is the field energy per unit area of the cell membrane,can be obtained from

where Δψ0is the transmembrane potential induced by an external field in the absence of cell deformation. When the deformation degree is enhanced, the membrane thickness d(θ)of cell is changed under different values of polar angle θ. As a result,the capacitance density and field energy density will be adjusted synchronously, and they are respectively calculated from

where Δψ is the transmembrane potential of the deformed cell.According to Eqs.(12)and(13),the changes and diversity for the capacitance density and field energy density can be calculated from
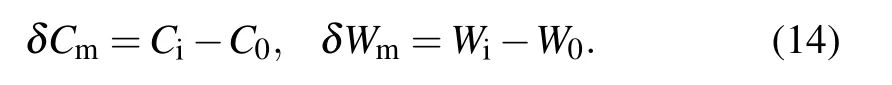
It is interesting to estimate the dependence of intracellular(or extracellular) ions concentration on the external applied electric field. Indeed, there is a resting membrane potential across the cell membrane in the absence of external field,which forms a potential barrier to balance the propagations of ions. According to the Nernst formula,the barrier height represented by the membrane potential is dependent on the ion concentration on the two sides of cell membrane. According to the Boltzmann’s formula,the relation[51,58]between the intracellular and extracellular ion concentration[C1]and[C2]of the cell can be approximately related by

where λ is the correction factor to describe the interaction between the applied voltage and the charged particle of the double lipid layer of the cell membrane, and VTis the thermal motion energy of particles expressed in the form of voltage.
When the cell is exposed to the electric field,an additional potential ΔV is generated on the cell membrane. And the potential barrier is modulated from v=V0to v=V0+ΔV. Also,the ion concentration[C1]on one side of the cell membrane is changed into[C1n]as shown below:

Therefore, the relative change rate of ions concentration on one side of the cell membrane driven by an external electric field is given by

When the applied electric field is triggered by a time-harmonic wave, and the across voltage or membrane potential is described in periodical-type ΔV = ΔVmcosωt. In the case of ΔVm<V0,equation(17)is replaced by

where ΔVmis the amplitude of the trans-membrane potential caused by the applied electric field.
3. Results and discussion
In this section, necessary numerical investigations are presented to find the dependence of biophysical properties on the external electric field and the electrical parameters of biocell. For possibly serving as contrast and reference, the typical values of the geometric parameters and medium parameters follow the setting criterion in Refs. [58,60], they being a0=10 µm, d =5 nm, εm=4.4×10−11F·m−1, εi=6.4×10−10F·m−1,εe=6.4×10−10F·m−1,σm=3×10−7S·m−1,σi= 0.3 S·m−1, σe= 1.2 S·m−1, and κ = 5×10−13erg(1 erg=10−7J). Firstly, the effects of geometric parameters and intrinsic physical parameters on the cell deformation are investigated in detail by analyzing the dependence of the relative elongation modulus k(f)/k0on the frequency f in an applied electric field. According to Eqs. (8) and (9), the cell shape is spherical at k/k0=0; while the cell shape is prolate(the semi-axis of the ellipsoid along the z direction is longer than along the x direction) at k/k0>0; when k/k0<0, the shape is the oblate.
The geometric parameters will be changed when the cell deformation occurs,in which the intrinsic physical parameters such as dielectric constant and conductivity have distinct influences on the gradient distribution of ion concentration and spatial potential. When the external electric fields with different frequencies are applied, the deformation of cell could be time-varying thus speeding up the ion propagation across the membrane channels. Due to the diversity of intrinsic parameters for the intracellular and extracellular media separated by the cell membrane,the cell will be deformed into different shapes. The dependence of the critical frequency on the electrical parameter of cell is shown in Fig.2.

Fig.2. Dependence of critical frequency fc on (a) conductivity σi, (b) dielectric constant of the internal medium εi, and (c) cell membrane εm separately,and(d)dependence of relative elongation modulus k(f)/k0 on frequency f of applied field,with θ =0.5,and other parameter values taking typical values.
In order to estimate the influence of cell parameters on cell deformation, figures 2(a)-2(c) show the relation curves between the critical frequency of the cell deformation and the cell parameters, and these parameters are in a certain range around the typical values of biological cell parameters, they being εm=4.0×10−11S·m−1-4.2×10−9F·m−1,σi= 0.039 S·m−1-0.807 S·m−1, εi= 3.5×10−11F·m−1-9.4×10−11F·m−1. The results in Fig.2(a) shows that the critical frequency of external electric field for inducting shape transition from prolate and oblate shape decreases when σiis selected to be a smaller value. Figures 2(b) and 2(c) display that the larger the value of parameters εiand εmare set to be,the lower the critical frequency of external electric field is and the more effectively the distinct shape transition will be triggered. The relationship between the critical frequency and the cell electrical parameters is nonlinear. Figures 2(a)-2(c)show that the critical frequency range is from 8.0×103Hz to 108Hz within the above ranges of the cell parameters values.Figure 2(d)shows the relation curves between cell relative deformation parameters and the frequency of external electric field for εm=1.24×10−11F·m−1, 8.8×10−11F·m−1, and 5.6×10−10F·m−1respectively,and the frequency is in a range of 103Hz-108Hz. That is,the dielectric constant and conductivity parameter have different effects on the shape transition of cell induced by external electric field. The dielectric constant ε is a complex quantity and defined by

where ε′, σ,and ω0are real permittivity, medium conductivity, angular frequency of electromagnetic wave, respectively.The real part of dielectric constant ε represents the permittivity, the imaginary part represents the loss, and the imaginary part is related to the conductivity. The larger the imaginary part, the greater the conductivity is and the worse the insulation performance. In the case of stronger conductivity, the higher frequency of applied electric field is effective in enhancing the polarization, and thus the shape deformation can be stabilized. On the other hand, the selection of a larger dielectric constant can enhance the intrinsic field of the cell and the lower frequency is required to keep the shape deformation of cell. The physical mechanism could be that higher conductivity can generate higher energy density(0.5σE2). And thus the external electric field needs high frequency to pump energy from the cell for triggering the distinct shape deformation of the cell. In addition,the electromagnetic stress is proportional to the dielectric constant. Therefore,a higher value for dielectric constant external electric with slow frequency will be more effective to stabilize the shape deformation.
In a practical way,a constant electric field is more available than a varying field. And complex electromagnetic induction can be induced in a medium when an electric field is applied with a high or an ultrahigh frequency. Therefore, to enhance the deformation effect, a smaller value for the conductivity parameter σiand higher value for the dielectric constants εiand εmcan be selected. Thus lower frequency in the applied electric field can be used.Furthermore,it is interesting to estimate the relation of cell deformation with the frequency of external electric field in a quantitative way.
Under the first order approximation for elongation modulus k,the deformation variable of the inner or outer surface of the cell membrane is estimated from

The distribution of the δr/a0(δr/b0)in the intersection line of the surface of the cell membrane with the xoz plane is given in Fig.3.
Figure 3 shows that when the angle is in a range of −55◦-55◦and 125◦-234◦, δr/a0(δr/b0) >0, otherwise δr/a0(δr/b0)<0,the cell shape is prolate,where the applied electric field is triggered at a frequency of 3×103Hz or 3×106Hz.When the frequency increases to 3×107Hz,the cell shape becomes oblate. The extensive calculation confirms that the deformation becomes more obvious when the frequency of applied electric field is selected to be a small value.

Fig.3. Distribution of δr/a0 (δr/b0)in intersection line of surface of cell membrane with xoz plane. Frequency values of applied electric field are selected to be 3×103, 3×106, and 3×107 Hz (data 1, data 2, and data 3),respectively. And other parameter values take the typical values.
As mentioned above, the cell and media can keep and save field energy. The capacitance of the membrane can be changed when cell deformation occurs. Therefore,the energy in the cell will be pumped and changed because the field energy is dependent on the intrinsic parameters of the media and capacitance for the cell membrane. The distribution of the δCmand δWmin the intersection line of the surface of the cell membrane with the xoz plane are given in Figs.4(a)and 4(b),respectively.

Fig.4. Distributions of(a)δCm and(b)δWm on intersection line of cell membrane surface with xoz plane,with parameter values E0, f,and a0 being selected to be 50 V/m, 1.0×106 Hz, 10 µm for data1; 50 V/m,1.0×106 Hz,15µm for data 2;60 V/m,1.0×106 Hz,10µm for data 3,and 50 V/m,3.0×107 Hz,10µm for data 4,and other parameter values taking typical values.
Data 1 curves in Figs.4(a)and 4(b)are the distributions of the δCmand δWmon the intersection line of the surface of the cell membrane with the xoz plane,where the parameter values E0,ω,and a0are 50 V/m,1.0×106Hz and 10µm,respectively. The cell radius a0in data 2 curve and the applied electric field intensity E0in data 3 curve are stronger than the value of data 1 curve in Fig.4. As shown in Fig.4,the absolute value δCmand δWmincrease with the increase of the cell radius a0and the applied electric field intensity E0. By comparing the curve data 1 with the curve data 4, it is also found that the frequency of the applied electric field affects values of δCmand δWm, where δCmand δWmare the difference in capacitance per unit area and in electric field energy per unit area between the deformation cells and non-deformation cells.Figure 4 also shows that the difference is larger at about 0◦(180◦)and 90◦(270◦), which is parallel or vertical to the applied field direction.Compared with non-deformable cells,the deformable cells will cause δCmand δWmto greatly deviate within a certain area.
Indeed, the membrane potential depends on the distribution of extracellular and intracellular ion concentration. And shape deformation in the cell will change the ion concentration and the membrane potential as well. The relative variation of ion concentration is defined by




Fig.5. Dependence of relative change−[C1]}/[C1]and relative variation[δC]/[C1]on frequency of applied field,where arameters are appropriately selected at θ =0.5,and other parameter values take the typical values:a0=10µm and E0=50 V/m for data 1;a0=15µm and E0=50 V/m for data 2;a0=10µm and E0=100 V/m for data 3.


Fig.6. Distribution for −[C1]}/[C1] and [δC]/[C1] on intersection line, where f =106 Hz, and a0 =10 µm, and E0 =50 V/m for data 1;a0=15µm and E0=50 V/m for data 2;a0=10µm and E0=80 V/m for data 3,and other parameter values take typical values.
In summary, the energy density in medium is dependent on the conductivity and inner electric field,while the electromagnetic stress mainly is proportional to the selected dielectric constant. To enhance the deformation effect, lower frequency in the external electric field is effective for generating a distinct deformation in the case of larger dielectric constant and lower conductivity of the cell. The larger the conductivity of medium, the larger the energy density will be, thus a low-frequency external field is required to suppress the energy distribution and then the deformation becomes achievable.
4. Conclusions
Based on the single-shell cell model and the theory of bio-electromagnetism, the boundary problem for spatial distribution of potential,and the physical factors for inducing the shape of cell to change under an external electric field, the changes of field energy and the ion concentration in the deformed cell membrane are calculated.It is found that the shape change of the cell is dependent on the geometric parameters,the intrinsic physical parameters of cell, the electric field intensity and the frequency of the applied electric field. Besides,the effect of cell shape deformation becomes distinct and can further shows biological significance when the cell is exposed to a high enough intensity electric field or expanded into large enough radius. In a practical way, the direction of external electric field can be adjusted to enhance the cell deformation effect and then ions pumping is enhanced to change the mode selection in neural activities.
- Chinese Physics B的其它文章
- Transport property of inhomogeneous strained graphene∗
- Beam steering characteristics in high-power quantum-cascade lasers emitting at ~4.6µm∗
- Multi-scale molecular dynamics simulations and applications on mechanosensitive proteins of integrins∗
- Enhanced spin-orbit torque efficiency in Pt100−xNix alloy based magnetic bilayer∗
- Soliton interactions and asymptotic state analysis in a discrete nonlocal nonlinear self-dual network equation of reverse-space type∗
- Discontinuous event-trigger scheme for global stabilization of state-dependent switching neural networks with communication delay∗

