微型航空发动机气体轴承-转子系统临界转速分析

张 强,张霞妹

(中国飞行试验研究院 发动机所，西安 710089)

对于微小型航空飞行器而言，与之相配套的微型航空涡轮发动机也成为国外航空发动机强国重点研究的关键技术之一[1]。微型航空发动机尺寸小，各部件结构简单，呈现出以下特点：(1)气体流道尺寸小(最小为6微米)；(2)采用单级离心压气机和向心涡轮结构形式，转子转速达到几十万～上百万转/分；(3)转子系统支撑使用气体轴承；(4)采用蒸发燃烧技术。微型航空发动机具有20～30倍于LiSO2电池系统的能量密度特征，在微型无人机、可携带能源及未来战争等领域具有重大应用前景，其研究分外引人注目。

美国以其高超的发动机研究能力在此方面遥遥领先。21世纪初，麻省理工学院研制了一台直径为20 mm的微型涡轮发动机，其转子转速高达一百万转/分。斯坦福大学研制了直径约50 mm的微型涡轮发动机，其转子转速约为五十万转/分。我国在此方面研究起步较晚。“八·五”期间，我国第一台微型涡轮发动机原理样机诞生于西北工业大学。在2006年，南京航空航天大学试制并运转了一台直径约为11 cm、转速约为10万转/分的微型涡轮发动机。我国在此领域的研究水平与美国相比差距较大。

对于微型发动机转子设计而言，由于转速超高，轴承一般选用以气膜润滑为机理的气体轴承。气体轴承的原理就是利用薄膜气流在高速转动下产生的粘性，从而产生对转子的支撑作用力。为了合理正确地设计微型发动机的气体轴承-转子系统临界转速，本文首先阐述了气体轴承内气膜作用力产生的机理，气膜作用力以及气膜等效刚度的求解方程；其次以气体轴承支撑的单盘转子为模型，对其临界转速和振型进行了求解；最后分析了影响转子临界转速的轴承参数，并提出了开展微型航空发动机气体轴承转子系统设计的意见和建议。

1 气体轴承等效刚度计算方法

图1为气体轴承原理图。轴承简化为圆环，其半径为R，长度为L，几何中心为Ob。转轴简化为圆柱，其直径为r，旋转中心为Oj。当Ob与Oj重合一致时，通常定义轴承与轴颈之间的半径差(R-r)为平均径向间隙C。

实际工作过程中，轴颈总是承受自身重量和气膜的作用力，因此两中心不会重合。通常定义Ob与Oj之间的径向距离为偏心距e，并且轴承内壁面与转轴外壁面之间的径向距离记作h。当转子在气体轴承腔内高速运转时，气体轴承气膜作用力F的方向总是与竖直方向存在一定的角度φo，称之为轴承姿态角。

图1 气体轴承原理图

根据气体轴承气膜润滑层内气体流动的连续性、边界层以及气体状态方程，可建立气体润滑轴承的基本方程，即[2-4]

(1)

式(1)中，p—薄膜压力(N/ m2)，h—轴承间隙(m)，R—轴承半径(m)，ω—转轴的旋转速度(rad/s)，μ—气体粘度(N·s/ m2)。

在等温稳态工况下，将公式(1)无量纲化，即为

(2)

(3)

因为

h=c+ecos(θ)

(4)

令ε=e/C(称之为偏心率),则公式(4)可以无量纲化为：H=1+εcosθ。

方程(2)和(3)是非线性椭圆型方程，求解后再对压力进一步积分即可获得气体轴承的气膜作用力F。通常将F和e的比值定义为气体轴承的等效刚度，用Kb表示，即

(5)

本文设计的气体轴承参数如下：R=7.5 mm，C=37.5 μm，L=15 mm，ε=0.8。气体常数取Rgas=287.5 N·m/kg·K，气体比热比γ=1.4，大气环境压力Pa=101 325 N/m2，气体温度T=288 K。需要说明的是，本文下面的计算结果在标准大气压力和15 ℃环境条件下是准确并适用的。当大气压力和温度不同时，应当以实际的环境条件重新进行计算。

在不同的转速下，计算了气体轴承的承载力和等效刚度。以转速为横坐标，以承载力和等效刚度为纵坐标，分别绘制了承载力和刚度随转速变化曲线，如图2和图3所示。可以看出，当选定轴承和转子参数不变后，随着转速的逐渐增大，气膜的承载力和等效刚度都随之提高。

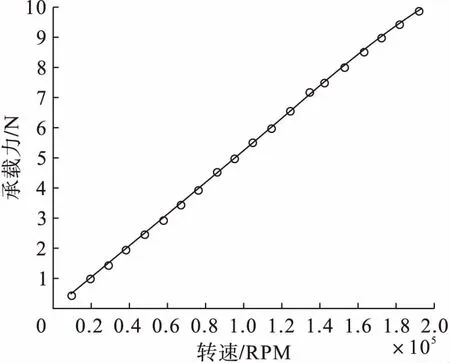
图2 不同转速下的气体轴承承载力

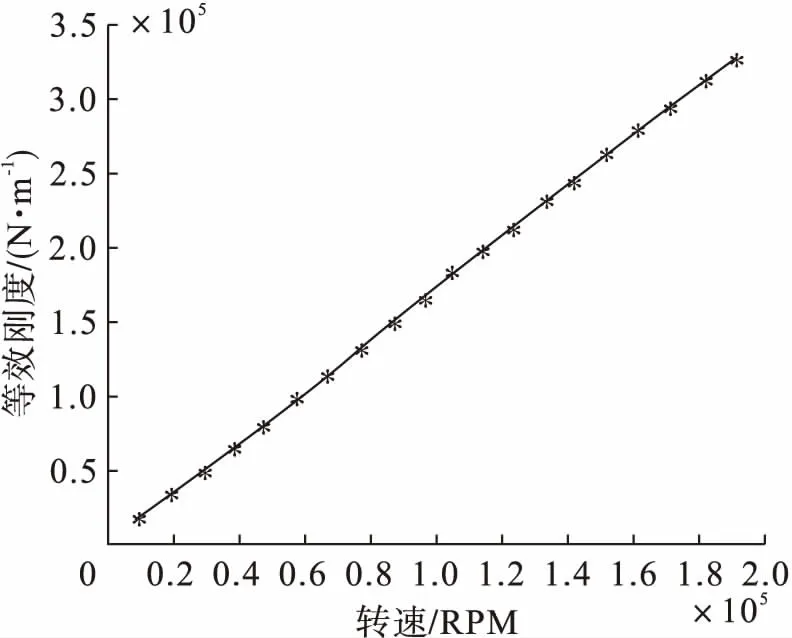
图3 不同转速下的气体轴承等效刚度

2 临界转速和振型计算

本文建立了简单的Jeffcott转子模型，如图4所示。转轴材料为不锈钢，直径为14.925 mm，长度 为0.1 m，重量为0.14 kg，弹性模量为2.1×1011，刚度为2.5×107N/m。单盘的材料为不锈钢，直径0.05 m，厚度0.003 m，重量0.046 kg。

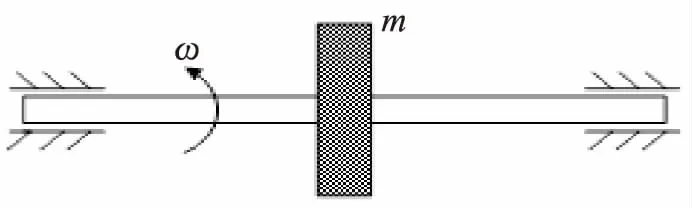
图4 气体轴承—转子系统示意图

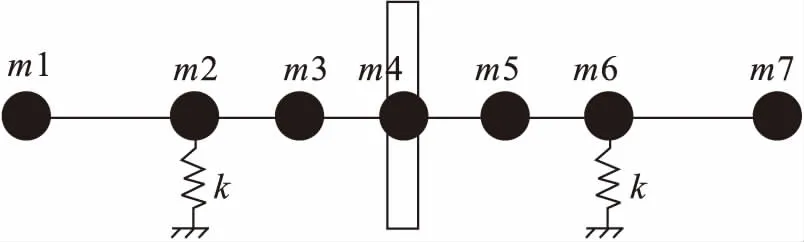
图5 气体轴承—转子系统临界转速计算模型

根据轴承和转子系统的质量分布特征，本文建立了转子系统的临界转速计算模型，如图5所示。计算结果表明，气体轴承转子系统的前两阶临界转速都比预想的低得多，其中一阶临界转速仅为1 870转/分，二阶临界转速仅为2 144转/分。这比转子的正常工作转速(通常在几万至十几万转/分之间)都低得多。这是由气体轴承的刚度较小所决定的。该转子的前两阶振型如图6所示。

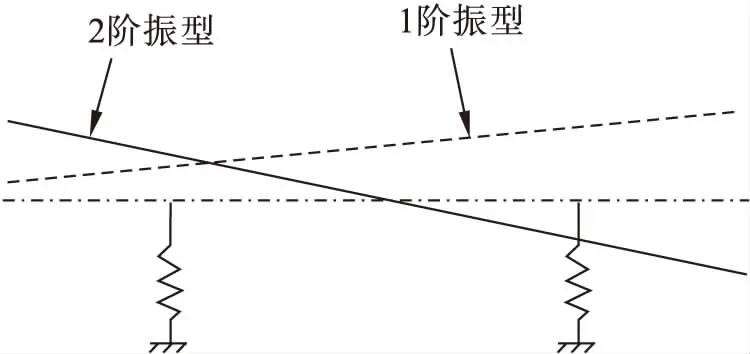
图6 转子前两阶振型图

3 轴承参数与临界转速的关系研究

气体轴承的关键设计参数包括平均径向间隙C、长度L与半径R之比(简称长径比)以及偏心率ε3个参数。为了正确地选择合适的轴承，并开展相应的转子系统设计，必须研究上述3个参数与转子系统临界转速之间的关系。需要说明的是，本文在研究轴承参数和临界转速的关系时，不考虑发动机的工况参数。

3.1 平均径向间隙与临界转速关系

保持其他参数不变，仅改变轴承的平均径向间隙，对转子临界转速进行计算，平均径向间隙与临界转速之间的关系如图7所示。从图7可以看出，当保持其它参数不变时，随着轴承平均径向间隙的增大，转子的临界转速逐渐减小。

图7 平均径向间隙与临界转速的关系

3.2 长径比与临界转速的关系

保持其他参数不变，仅改变轴承的长径比，计算了转子临界转速，长径比与临界转速之间的关系曲线如图8所示。从图8可以看出，当保持其它参数不变时，随着长径比的增大，转子系统的临界转速逐渐提高。

图8 长径比与临界转速关系曲线

3.3 偏心率与临界转速的关系

保持其他参数不变，仅改变轴承的偏心率，计算了转子临界转速，偏心率与临界转速之间的关系曲线如图9所示。从图9可以看出，当保持其它参数不变时，随着偏心率的增大，转子系统的临界转速也逐渐提高。

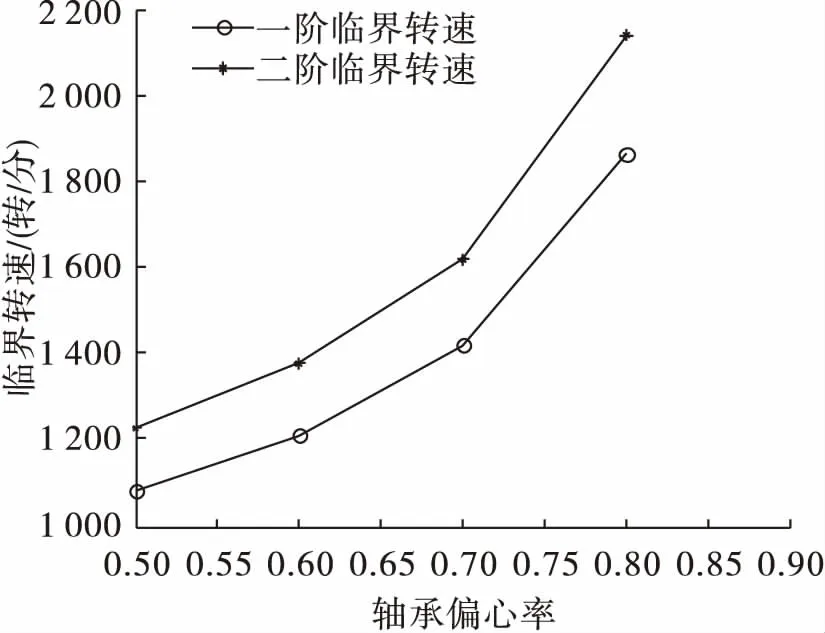
图9 临界转速与偏心率的关系

4 结论

本文研究了气体轴承的承载力、等效气膜刚度以及转子系统的临界转速计算方法，并对平均径向间隙、长径比和偏心率等3个参数与临界转速之间的关系进行了分析，得出以下结论：

(1)平均径向间隙对临界转速的影响程度有限，临界转速范围在800～3 000转/分之间。这是因为间隙不能太小，否则容易导致转子与轴承之间发生碰磨。

(2)偏心率对临界转速的影响程度有限，临界转速范围在1 000～3000转/分之间。这是因为偏心率不能太大，否则容易导致转子与轴承之间发生碰磨。

(3)长径比对临界转速的影响程度最显著，临界转速范围在2 000～8 000转/分之间。轴承半径设定之后，仅需要增加轴承长度，即可明显改变转子的临界转速。

因此，在设计气体轴承-转子系统的临界转速时，可以设定轴承的平均半径间隙和偏心率不变，仅通过改变轴承的长径比，即可方便地控制气体轴承-转子系统的临界转速。