考虑跑道的航班停机位分配研究

袁 媛， 翟好鑫

(沈阳航空航天大学 经济与管理学院， 沈阳 110136)

随着航空运输业的快速发展，合理地计划使用机场各项设施资源已经成为目前急需解决的问题。有限的停机位资源也成为制约大型机场发展的主要原因，而随着多跑道呈现出的常态化趋势，许多机场开始通过增建跑道等方式来提高机场容量，以缓解航班延误。多跑道运行系统在一定程度上提升了机场的可用容量，但同时也使得机场运行形势更为复杂，这就对停机位分配提出了更高的要求。对于滑行道结构复杂的多跑道机场而言，整个飞行区的运行安全与滑行效率更为重要[1]。因此，研究和评估多跑道机场的停机位运行效率具有非常重要的理论意义和实际价值[2]。

为了满足机场运行的安全性和高效性，机场急需更加高效、均衡的航班调度策略，以实现精细化的航班流量管理。本文考虑相邻航班时间间隔和推出冲突，基于飞行区航班场面滑行时间建立停机位目标优化模型，并采用实例进行分析得到较优分配方案，以验证模型的有效性和合理性以及多跑道对于停机位分配的重要性。

1 多跑道研究现状

当前对停机位分配的研究主要以机场飞行区以外的部分为研究对象，如以最小化旅客行走距离、最小化停机位空闲时间、最小化旅客登转机时间等作为目标函数进行优化。但这些研究所用的变量在机场实际运行中获取困难，而不考虑飞行区部分进行停机位分配将造成更多的航班延误以及跑道滑行道冲突，减小机场地面容量。

关于航班在多跑道机场上的停机位分配问题，近几年中外有较多研究。一些学者从飞行区时间考虑，文献[3]考虑了旅客、航空公司等方面的综合利益进行停机位分配。从机场运行安全角度出发，文献[4]建立了航班动态排序模型，文献[5]最小化离场航班滑行时间，以寻求最优的跑道分配方案。而关注求解算法的停机位分配文献中，文献[6]采用贪婪算法和元启发式方法以最小化航班延误成本建立模型，文献[7]采用蚁群算法对多跑道航班协同调度优化模型进行仿真，文献[8]则开发了epsilon约束算法，通过实例验证模型的可行性和算法的有效性，为机场资源优化研究领域提供重要参考，文献[9]通过具有创新性的非支配排序遗传算法来进行多跑道下的进港航班调度，文献[10]基于飞行区建立了仿真模型，提高了滑行系统航班容量的同时也减少了航班延误时间。

2 停机位分配模型

2.1 研究假设

针对所研究的多跑道停机位分配问题提出假设条件：在停机位分配计划期中，机场制定决策所需要的航班计划、机场资源信息都是已知的，研究过程中不考虑过夜航班、备用停机位和维修机位，远端停机坪容量无限大。

2.2 符号说明

F： 研究过程中提供的所有进港航班集合；

D： 研究过程中提供的所有离港航班集合；

G： 研究过程中提供的所有停机位集合；

G1：研究过程中提供的所有近机位集合；

R： 研究过程中提供的所有跑道集合；

N： 研究过程中机场的近机位总数， 其中N+1为远端停机坪；

i： 所有到港航班对应序号，其中i∈F，i1和i2为两相邻到港航班；

j： 所有离港航班对应序号，其中j∈D，j1和j2为两相邻离港航班；

k： 所有停机位对应序号，其中k∈G；

r： 所有跑道对应序号，其中r∈R；

Ai：所有航班i的预计进港时刻；

Lj：所有航班j的预计离港时刻；

ti： 航班类型i分为大、中、小3种机型，分别用2、1、0表示；

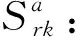
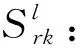
v： 航班在飞行区的平均滑行速度，对大型飞机取v=18 km/h，对于中、小型飞机v=7.2 km/h。

2.3 约束条件

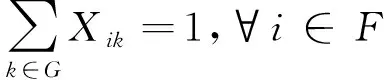
(1)

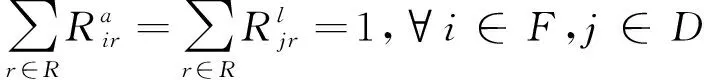
上述公式是定向突变法的核心，定向突变的实质在于保护优势个体的优势基因，同时促进劣势个体进行主动突变。在整个突变的过程中，群体的基因多样性不会因为优势个体的保留而减少，因为存在劣势个体的突变，保证遗传算子正常发挥进化和重组效应，从而提高群体的多样性。

(2)

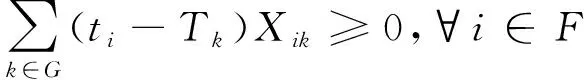
(3)

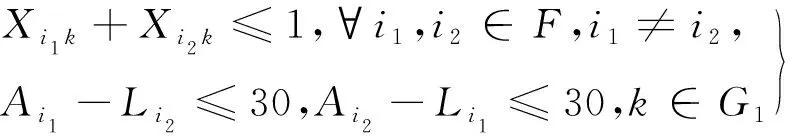
(4)

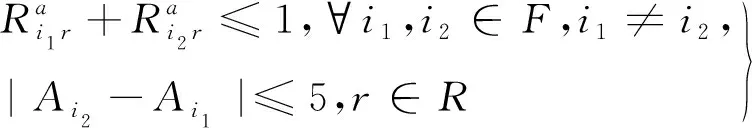
(5)

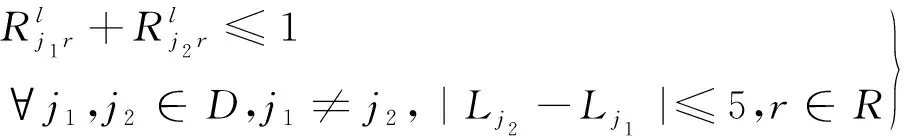
(6)

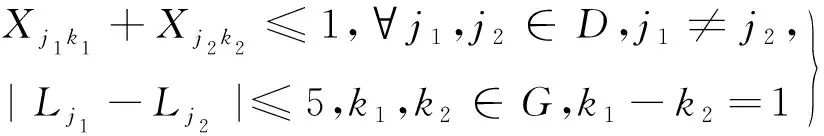
(7)

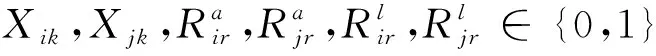
(8)

式(1)为航班i对停机位k占用的唯一性约束。

式(2)为进(离)港航班对进(离)港跑道r使用的唯一性约束。

式(3)为停机位k所容纳的最大机型与航班机型相匹配约束。

式(4)表示对于所有近机位，相邻两个航班停靠在同一机位的时间间隔需有限制，取同一近机位的相邻两个航班的间隔时间限制为30 min。

式(5)、式(6)表示对于所有进(离)港跑道，相邻使用同一跑道的两个航班需满足安全时间间隔，取同一进(离)港跑道相邻两个航班的间隔时间限制为5 min。

式(7)为两个相邻近机位的推出冲突约束，取相邻两个近机位的安全推出时间间隔为5 min。

式(8)为0-1变量约束。

3 优化目标

多跑道机场的停机位分配问题影响到航空公司运行效率、机场设施资源使用率以及旅客满意度等多个方面，其中最直接的影响就是飞机航班滑行时间，因此在满足安全约束的前提下，分别基于单跑道和多跑道建立最小化航班场面滑行时间的停机位分配优化模型，以便于案例分析。

3.1 不考虑跑道时飞机场面滑行时间

以往研究往往不考虑跑道对停机位分配的影响，机场支持所有飞机同时起降，不考虑同一进(离)港跑道相邻航班时间间隔约束，因此此时建立最小化进离港航班场面滑行时间目标函数为

(9)

3.2 多跑道时飞机场面滑行时间

多跑道机场的兴起和建设，直接影响航班运行效率。因此考虑跑道进行合理分配停机位对于提高飞机滑行效率很有必要。对于客机，场面滑行效率影响到旅客等待时间及行走距离，对机场的综合运行效益至关重要。而对于货机，航班进离港时对于跑道和停机位的选择也会影响货物到达航站楼的距离，不同载重的货机场面滑行速度也有所不同。因此，基于多跑道进行分析，建立最小化进离港航班场面滑行时间目标函数：

(10)

4 实例分析

采用国内某机场工作日8：00—22：00出发或到达的116个航班和20个典型的近机位、一个远端停机坪进行案例分析，其中G01-G12机位为大型机位，G13-G17号机位为中型机位，G18-G20号机位为小型机位。

通过实例进行分析，合理时间内求解出对应的停机位分配模型，得到最优的停机位分配方案。就目标函数值而言：不考虑跑道情况下，飞机场面滑行时间为Z1=4 201.042 min，而考虑跑道后滑行时间为Z2=3 868.194 min，同等条件下相比于不考虑跑道时减少了332 min，滑行效率提升了7.92%。单跑道与多跑道情况下的停机位使用情况对比如图1所示。

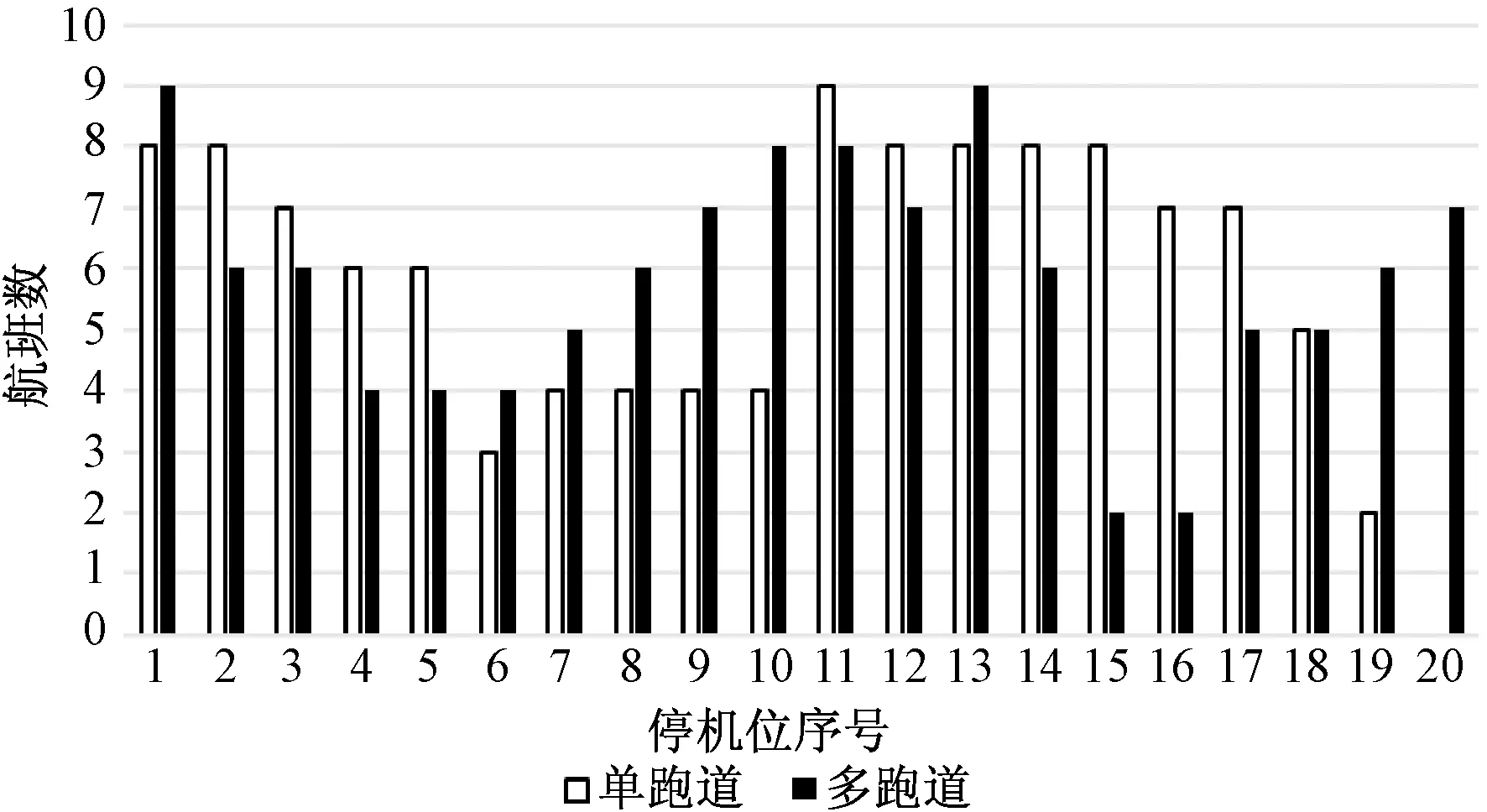
图1 停机位使用情况对比

由图1可知，多跑道情况下停机位使用更加均衡，这样可以使机场工作人员以及设备资源更加均衡使用，避免出现不公平、不平衡现象。此外，考虑跑道的情况下，停机位分配方案会更加偏向于使用平衡双跑道距离的停机位位置，这样使得航班场面滑行时间更少，保障了机场运行效率的提升。最后，两个模型分配方案均没有使用距离较远的远端停机坪，也一定程度上节省了航班滑行时间。

较优方案选择：由于考虑多跑道将提高机场运行效率，场面滑行时间更短，以此将带来更好的机场各方满意度，故模型求解后最优的停机位分配方案如表1所示。

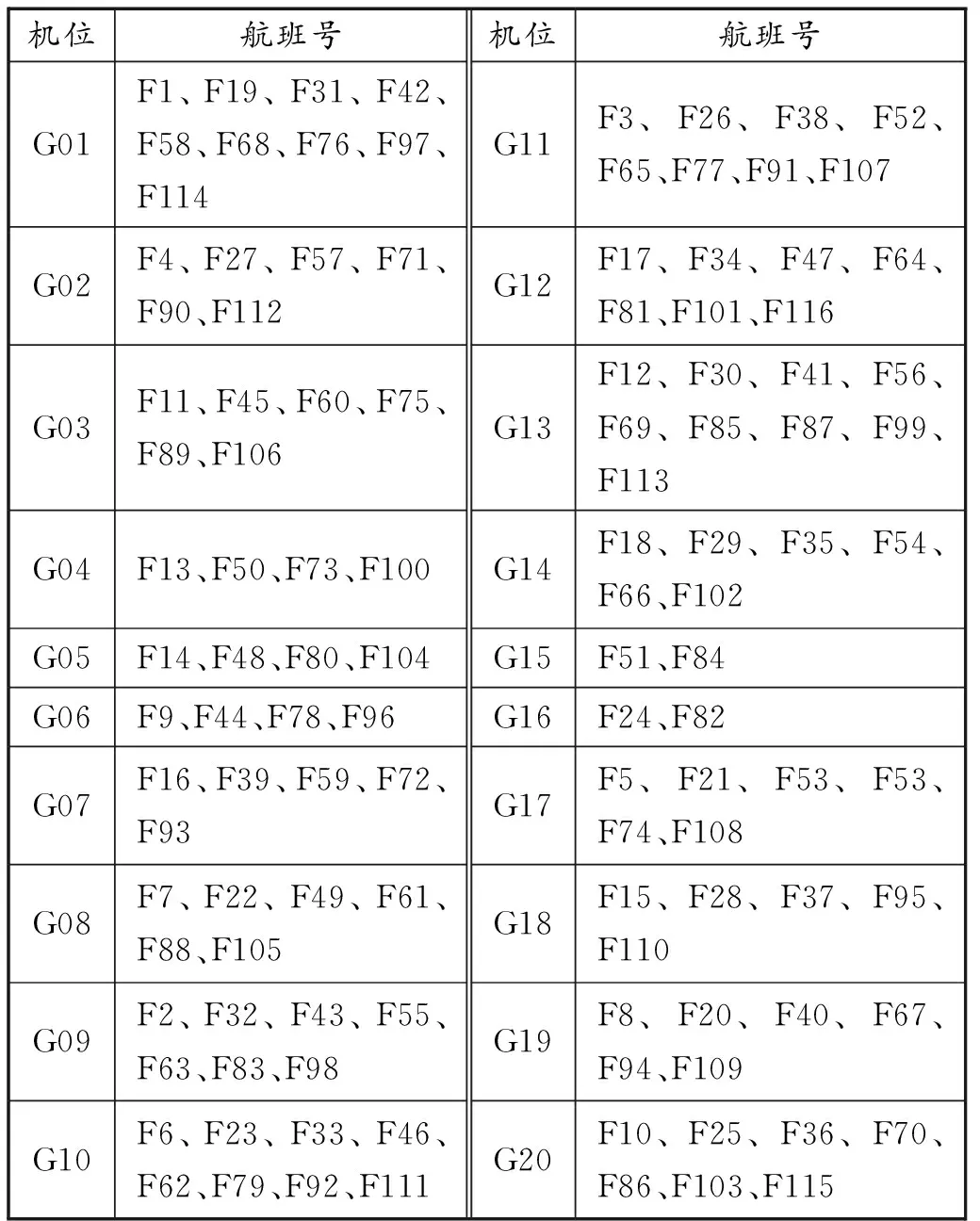
表1 最优分配方案

5 结论

在满足安全性的前提下，基于国内某机场建立了最小化航班飞行区滑行时间的停机位分配优化模型，并且对比了单跑道和多跑道下的滑行时间，最终选择多跑道下的最优分配方案。结果表明模型优化的可行性和适用性，验证了多跑道对于提高机场运行效率、保障机场资源使用均衡方面的重要性。下一步将在多跑道对于机场综合运行效率方面的影响进行深入研究。