针对时间序列数据挖掘的双加权聚类集成

胡健，王海林，肖鹏，尹君

（云南电网有限责任公司信息中心，昆明 650217）

0 前言

时间序列是一种广泛存在的数据，是由客观对象的某个物理量在不同时间点的采值按时间顺序排列成的序列数据，时间序列客观记录了所观测的系统在各个单位时间点上的状态值，所以可以通过研究时间序列数据来辨识、重构和预测所观测系统的行为模式。时间序列具有普遍存在性，多媒体数据，金融数据，气象数据，人口普查数据都是时间序列数据类型。研究如何有效地从这些复杂的海量时间序列数据中挖掘隐藏的、有价值的信息与知识，具有重要的理论价值和现实意义。时间序列数据挖掘（Time Series Data Mining）已成为数据挖掘研究领域中主要的研究对象[1]。时间序列数据挖掘巨大的科学意义与应用价值正在受到世界许多国家学术界、工业界和政府部门的普遍重视。2005 年，香港中文大学的研究者做了一项关于数据挖掘研究中最具挑战性问题的研究报告，将时间序列数据挖掘列为数据挖掘中最具挑战性的十大研究方向之一[2]。2014 年10 月，Twitter 公司开源了云环境时间序列数据断层检测工具Breakout[3]。2012 年，奥巴马政府投资2 亿美金启动“大数据研究和发展计划”，并在2017 年发布了第二轮大数据研究项目，其中白宫科技政策办公室正在建立流行病“天气预报”项目，旨在利用大数据方法，能够尽早对流行病作出识别和预测，以便预做准备，减轻症状，其本质就是时间序列数据挖掘[4]。

时间序列数据挖掘与传统的数据挖掘最大的区别在于其数据的时效性与有序性，是一个发现潜在有用的，与时间属性相关的信息与知识的过程，其主要包括时间序列相似性挖掘、特异性挖掘与规律性挖掘。数据挖掘技术大致包括：统计学方法、聚类分析、决策树技术、人工神经网络、规则归纳，以及可视化技术等等，本课题将主要研究时间序列数据挖掘的聚类分析技术。尽管研究人员在时间序列聚类分析的研究上已经取得了许多成果，但由于时间序列数据本身具有非常复杂的特性，如：复杂时间相关性，高维度，海量性、噪声干扰，使得时间序列数据挖掘的工作充满挑战，依然面临以下亟待解决的关键问题[5]：

1）虽然研究人员己经针对时间序列提出许多特征表示（representation）方法，但是每一种方法对于时间序列信息的还原都具有片面性，某一种特征表示方法只能提取时间序列中某些特征信息，并且通常无法全面地反映出目标数据集的簇结构信息，有些特征甚至会混淆数据的簇结构,导致聚类算法失效。如何选取最佳的有助于呈现目标数据集的聚类分析的特征表示仍然是一个棘手的问题。

2）现有的时间序列相似性度量用多种距离公式，如，欧氏距离(Euclidean Distance) ，马氏距离（Mahalanobis Distance) ，对数似然距离（log-likelihood Distance），动态时间弯曲距离（Dynamic Time Warping）等[6]。但是在实际操作中，每一种特征表示方法都有其对应的最佳相似性度量方法。如何确定最佳的匹配仍需要大量的先验人为应验。此外，很多相似性度量公式具有较高的计算复杂度，针对高纬度，海量的时间序列数据集进行聚类分析时，需要较高的计算资源，而且都含有需要用户设置合理的参数，同时在聚类过程中，待聚类的数据都是在距离闽值的强制作用下聚合或分离，无法准确体现数据对象间自发，天然的聚散关系。

3）针对时间序列所使用的聚类算法普遍具有单一性，没有一种聚类算法可以普遍适用于各种时间序列数据集所呈现出来的复杂簇结构。一种聚类算法一般只适合于某种情况的聚类分析。此外，在进行聚类之前都需要用户事先确定要得到的聚类的数目（类数）。然而在现实数据中，类数是未知的，通常要经过不断的实验来获得合适的类数，以得到较好的聚类结果。

集成学习(Ensemble Learning) 是指利用多个学习机解决一个问题。随着其飞速发展，研究人员尝试使用此类方法解决上述时间序列数据挖掘的难点问题，并取得了一系列创新性研究成果。聚类集成学习（Clustering Ensemble）的目的是通过集成多个互补的聚类结果以得到一个高可靠性的聚类分析系统，旨在产生泛化能力强、差异大的多个成员聚类器，充分发挥每个成员聚类器在各自聚类性能上的优势，获得比单个成员聚类器都要好的聚类集成结果。与单一的聚类算法相比，聚类集成学习具有三大优势[7]：聚类集成结果具有更高的精确度；聚类集成学习可以发掘单一聚类算法无法发掘的簇信息；聚类集成学习对于复杂环境，如：噪声，异常数据点，采样变化，有较强的抗干扰能力。一般通过提高成员聚类器的聚类性能以及增加成员聚类器的差异性（Diversity）来达到提高集成性能的目的。但现有的聚类集成学习算法依然存在诸多问题[8]，具体分析如下：

1）如何在没有先验知识的条件下，合理地组合大量的初始聚类分析结果以达到最优融合，仍然存在诸多亟待解决的问题。

2）由于聚类集成算法是一种无监督学习过程，因此，如何正确有效地识别类簇的本征类数仍然是一个棘手的问题。

针对上述问题，本课题在非监督学习的理论框架内，深入研究基于生成模型和特征表示的时间序列数据挖掘算法，提出两种新型的双加权聚类集成学习模型，从不同角度进一步提高集成算法在时间序列聚类分析中的性能。本课题将目前时间序列聚类算法以及聚类集成算法中的几个关键性难点问题（包括：时间序列特征表示和生成模型表示方法；多成员聚类器的产生和融合；以及聚类分析中的类数自确定）纳入统一的算法框架，为复杂多样的时间序列数据集的聚类分析提供了一套可行的通用技术路线。

1 算法描述

本课题提出的算法模型由三个模块组成，包括了特征抽取，初始化聚类分析，双加权聚类集成学习。其拟算法流程如图1 所示。模型构建的研究方案如下。

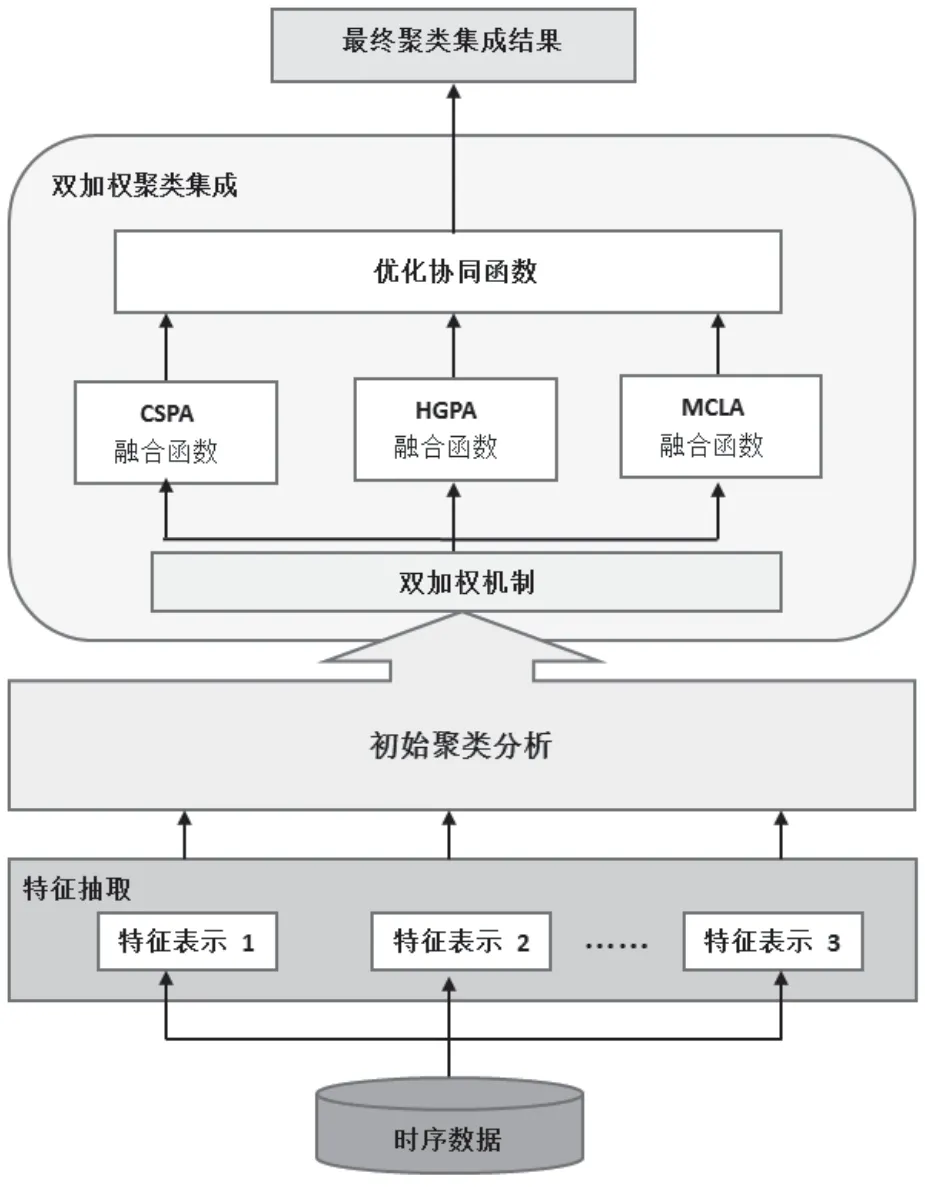
图1 基于多特征表示的双加权聚类集成模型

1.1 时间序列特征抽取(representation extraction)

时间序列表征通常可以分为两大类:分段式的（piecewise）和全局式的（global ）。一个分段式的特征表示(piecewise representation)根据一个分割标准把高维的时间序列向量分解成一系列的分段向量，然后对每个分段做特征提取，所有分段的特征表示按序排列组成一个完整的分段式特征表示(piecewise representation)，例如，自适应分段常数近似(Adaptive Piecewise Constant Approximation) 和分段式主成分分析（piecewise Principal Component Analysis）。在全局式特征表征（global representation）中，我们用基函数来模拟目标时间序列数据集，因此，基函数的回归系数构成了时间序列的特征表示，例如，多项式拟合(polynomial curve fitting)，离散傅里叶变换(discrete Fourier transforms)，和离散小波变换(discrete wavelet transforms)。一般情况下，分段式(piecewise)和全局式(global)的时间序列特征表征具有一定的互补性。分段式注重局部信息的表述，但容易忽略全局信息。相反，全局式可以很好的还原时间序列的整体特征，但对局部信息的提取不够完整。在此模块中我们将选取多个特征表示方法，使其对时间序列的特征描述上具有最大程度的互补性。

1 . 2 初始化聚类分析( initial clustering analysis)

在初始聚类分析模块中，我们在不同的特征空间里，给定不同的初始化设置，对目标数据集进行聚类分析，如使用k-mean 算法，会产生多个不同的划分。由此可以有效地增加各划分的差异性（Diversity），从而提高聚类集成学习的性能。以往的研究证明聚类集成学习的性能取决于初始聚类分析的质量和其产生的划分的差异性。

1.3 双加权聚类集成(Bi-weighted clustering ensemble)

为了确保类簇和它们的划分根据其重要性对融合产生建设性的贡献，我们引入了一个双权重方案以优化输入划分的融合。这样，不仅将权重根据他们的聚类质量全局地分配到了输入划分，而且权重的局部分配能自适应于类簇本身产生的对应划分。

1）双加权框架

给出一个距离变量D，加权聚类集成的融合函数是为找出接近多重输入划分的一个融合划分Pr，输入划分是从目标数据集中获得。因此，融合用公式可以表示为成本函数的最小化，如下所示：

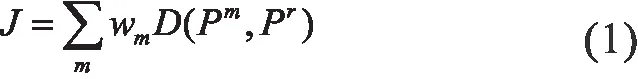
其中wm指的是划分Pm的权重，

在基于模型的聚类中，每个输入划分Pm被表示为一个概率分布的混合其中是混合模型参数，Km是每个输入划分的类簇数，表示聚类，p(km) 表示先验概率。基于KL 距离，公式(5)中的花费函数可以被进一步地推导为：

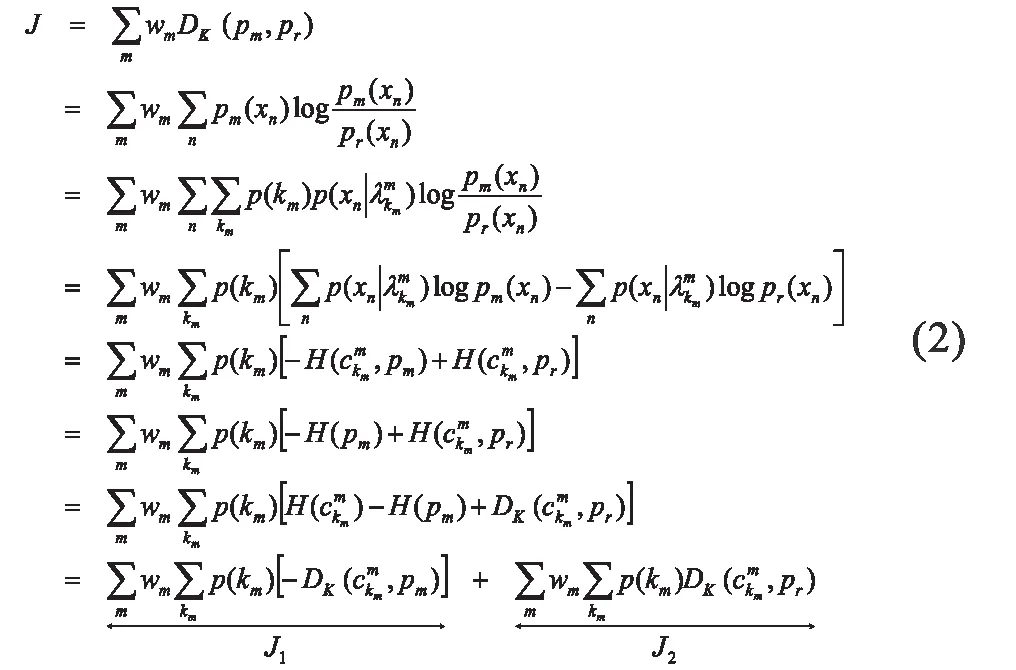
公式(6)中的花费函数可以被分解成两个子花费函数J1 和J2，这表明了一个聚类集成算法的性能依赖于聚类集成和输入划分的质量。其中，第一项J1 对应于输入划分的质量，J1 的值越小意味着输入划分的质量越好。事实上，聚类的目的在于将目标数据集划分到不同的组或类中，使得同一个分组/类中数据点具有较高的相似性，相似性由一个类间距离来确定，不同类间的相异性通过集群(类簇)的距离来确定。也就是说，Dlk测量和划分Pm中剩余的类的集群内间距离，其中，表示类数据点的相似性。因此，输入划分Pm的聚类质量可以用公式表示为：

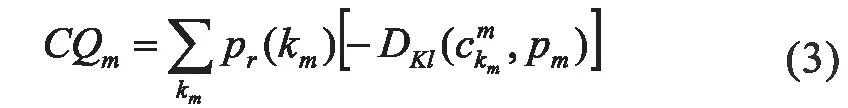
CQm的最小值标识着输入划分的最佳质量，其中类簇集群内部的距离应该小，而类簇间的聚类应该大。

直观地，划分权重应该由J1 的最小花费确定，其中较大的权重应该被分配给较好的划分质量，较好的划分质量由较小的CQm值所决定。然而，这种简单的方法可以分配一个单一的最大权重给具有最小CQm值的输入划分，同时其他所有的权重都被置零。在这种情况下，融合函数转变成了选择函数。为了是所有的输入划分促成融合划分，我们在J1 中引入了一个表示划分权重负熵的正则项wmlogwm，构成了一个正规化的花费函数：

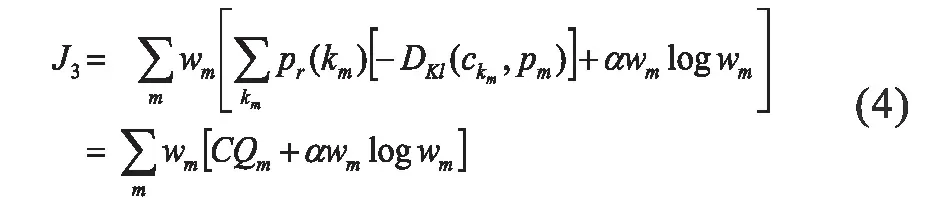
其中α≥0 是一个拉格朗日乘数，控制着额外正则项的强度，增加它的值将会加大输入划分的enthusiasm。在我们的仿真实验中设定α=0.5。

因此，适当的划分权重可以通过J3 的最小划分来确定[51]：

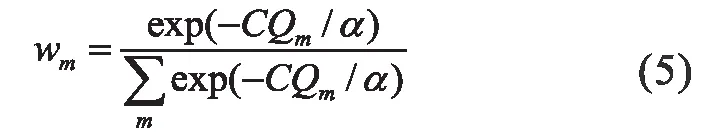
一旦得到了输入划分和对应的权重，J 的第一项J1 就被固定了，所以聚类集成的性能主要由J2 控制。因此，J2 的最小值等价于J 的最小花费。为了优化这个过程，我们引入了双层加权方法来判定接近所有类簇的融合划分。在花费函数J2 中，第一层权重是通过公式(9) 得到划分权重，第二层权重是类簇的权重，可以被定义为：

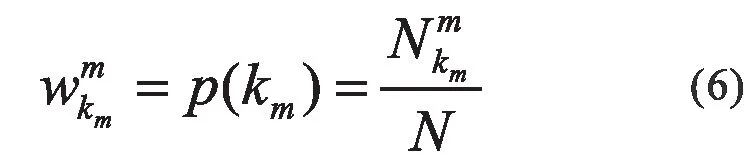
其中是具有划分Pm的聚类中数据点的数目，而N 是所有数据点的总数。2）共识函数

现有的聚类集成技术应用了三个hyper graph-based 的融合函数来产生融合划分。因此，需要将大量的输入划分通过连接所有的二进制成员指示器映射到一个hypergraph。指示器是映射每一个输入划分Pm到一个邻接矩阵以制作一个超图得到，为了进一步改进在我们设计方案中hypergraph-based 融合划分，我们提出了一个加权的hypergraph，定义如下：

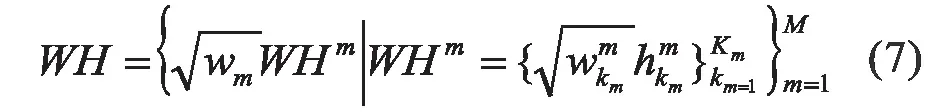
为了导出集成的融合划分，我们应用了三个融合函数来确保不同的视角都被考虑到。包括了基于聚类的相似性划分算法(CSPA)、hypergraph-partitioning algorithm (HGPA)和the meta-clustering algorithm (MCLA)。其中CSPA是一个简单的融合函数，距离矩阵S 在加权的hypergraph 中对所有的划分进行加密，派生于邻接矩阵WH:S=WHWHT，then the similarities yielded from multiple partitions are used to recluster all the sequences to yield a consensus，HGPA 提供了替代的融合函数，通过铸造聚类集成问题，关于通过剪切最小加权超编怎样划分加权的hypergraphy，不像CSPA 把局部分段相似带入计算，HGPA 关心跨域不同划分序列的相对全局关系。最后，元聚类算法(MCLA)通过聚集多个输入划分实现融合。其基本思想是重新聚类加权的超边(hyper-edges)，生成融合函数，聚类的总数减少到由用户指定的元聚类的一个小数目。

3）目标函数

没有先验知识，就不可能提前选择一个合适的函数以形成聚类集成。既有的解决办法都是使用归一化互信息(NMI)根据目标函数[45]来测量任何两个划分之间的一致性，用公式表述如下：

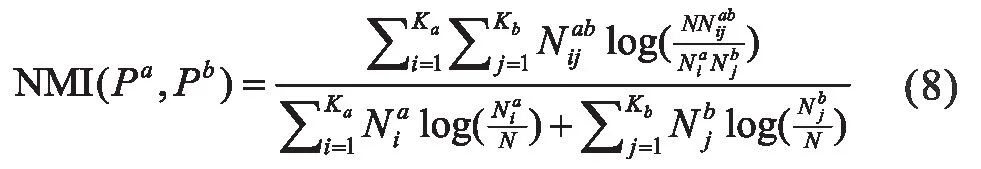
其中Pa,Pb表示两个划分的标签，将N 个对象的目标数据集划分到Ka和Kb两个类簇中，是类簇和之间共享对象的数目，和分别表示和的对象数目。

根据公式，最优融合划分通过搜寻从HMM K-models 聚类集成中获得的M 个划分的最大平均互信息来确定，为此，通过下面的优化方程来确定这三个函数的最佳融合。

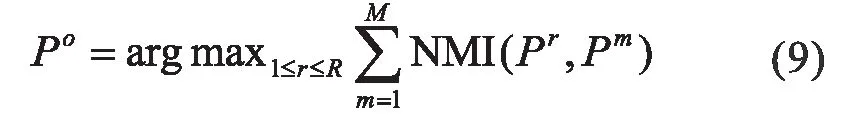
其中Pm是HMM 的K-models 生成的第m个划分，Pr是第r个融合函数产生的融合划分。总之，融合函数筛选出的划分Po作为给出时序数据集的最优融合划分。

2 实验验证

为了评估总体上对时间数据进行聚类的方法的性能，我们通过使用时间序列集合作为测试数据集来进行模型验证[52]。该基准数据集包含16 个合成或真实时间序列的数据集。表1 中列出了有关所有16 个数据集的特定信息，包括每个数据集中的类数，时间序列数和时间序列长。

表1 时间序列基准数据集信息

为了实验效果比对，我们最初在时间序列的基准集合上测试了5 种技术，包括K 均值，基于动态时间规整（DTW）的K 均值[53]，基于HMM 的K 模型，HMM 混合聚类和HMM 混合元聚类，其中K-mean 算法的结果由基准收集器提供。为了检查所提出的双向加权方案的有效性，我们还将我们的方法与其HMM 混合元聚类集成体的原型进行了比较，并观察了引入的双向加权方案如何能够有效地提高聚类集成体的性能。对于基于HMM 的聚类算法，HMM 的状态数对于时间序列建模至关重要。但是，此类信息通常不可用，因此我们只能对一系列状态号进行穷举搜索，其中最佳状态将最适合估计的HMM，从而导致最大的对数似然性，即所谓的“前进”和“后退”算法[38,39]。在我们的实验中，每个时间序列的最佳状态数分别确定为6、2、4、9、2、6、3、10、8、8、9、6、7、8、2、3 包括在内。每个数据集的类别编号K *也用于所选基准中。由于我们提出的算法具有自动选择模型的能力，因此我们简单地将K 值设为预设范围（K＞1）中的簇数。

我们使用最佳参数设置将每种算法运行10次，表2 中列出了每种经过测试的算法的最佳结果，从中可以看出，我们的方法在16 个数据集中的8 个上获得了最佳性能。相比之下，基于DTW 的K-mean 可以在三个数据集上获得最佳结果，而所有其他数据只能分别在一个数据集上获胜。对于基准测试，这些结果是在手动优化和预先给出初始簇/ 状态数的条件下获得的，这实际上使我们提出的算法处于不利的位置。

为了说明我们提出的算法在预先确定给定数据集的聚类数方面具有优势，我们用符号*报告了分类精度的实验结果，以表明在确定正确的聚类数的情况下达到了准确性。 可以看出，我们的方法能够在16 个数据集中的12 个数据集中找到正确的群集编号，但是标准模型选择技术（BIC）只能设法找到7 个数据集的正确群集编号。

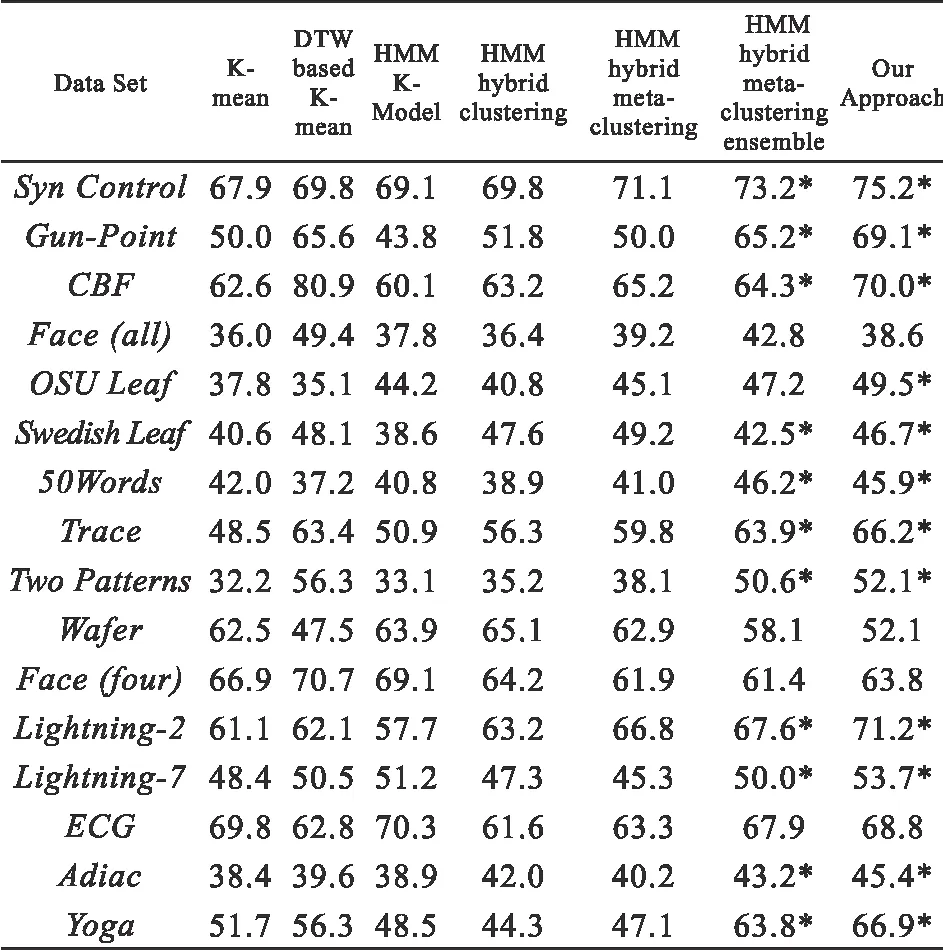
表2 时间序列基准上的聚类算法的分类准确性（%）

在此实验模拟中，从不同的角度显示了许多方法来解决时间数据聚类问题。作为基准算法，K-means 仅使用欧几里得距离来基于局部比较来测量时间序列之间的相似性，其中时间序列是点对点对齐的。这种基线技术无法获得令人满意的结果，尤其是当时间序列的观测值发生偏移时，例如Gun-Point，CBF 和Two Patterns。为了克服这些限制，通过使用动态编程技术开发了动态时间规整（DTW）距离[53]，该技术从两个时间序列之间的最佳对齐中确定了规整距离。从表2 中所示的结果可以看出，在16 个数据集中的12 个数据集中，基于DTW的K 均值优于标准K 均值。但是，对于OSU Leaf，Lightning-2 和Yoga 等高维时间序列，基于DTW 的K-mean 所获得的结果几乎没有改善，但比其他算法花费的时间要长得多。尽管基于HMM 的聚类技术设法通过考虑时间序列的时间信息来捕获聚类结构，但所取得的进步仍然有限。对表2 中列出的结果进行的比较研究表明，我们的方法在模型选择和分类准确性方面均达到了最佳性能。它通常适用于高维时间序列，并在最长的时间序列（包括OSU Leaf，Lighting-2，Lighting-7 和Yoga）上获得最佳结果。此外，表2 还表明，我们的方法通过赢得16 个数据集中的13 个数据集，胜过HMM 混合元聚类集成作为其原型，这显然证明了拟议的Bi-weighting 方案的有效性。

3 结束语

在本文中，我们报告了一种新颖的基于HMM 的混合元聚类与集成技术相结合的时态数据聚类，并进一步提出了从对聚类集成的目标函数进行形式分析得出的Bi-加权方案。在各种时态数据集上的仿真结果表明，我们的方法在时态数据聚类分析中取得了令人鼓舞的性能，适用于未知环境中的应用。结果，对于我们提出的方法，可以突出四个主要优点，包括：（i）通过基于HMM 的分区聚类的集成来解决模型初始化问题；（ii）可以通过在与DSPA 关联的共识分区上应用基于HMM 的层次聚类来自动确定适当的聚类编号。（iii）根据分区和集群之间的最佳协同作用，研究了一种Bi-weighting方案来获得改进的集群集成解决方案；最后（iv）通过应用复合模型来驱动最终精炼过程，可以有效地捕获簇的内在结构。

可以考虑进一步研究以解决基于HMM 的聚类的状态发射概率问题。在文献报道的现有工作中，通常将状态发射概率建模为多元高斯模型。如何为单个状态发射函数选择高斯分量的数量仍然是一个悬而未决的问题。通常，已经发现多元高斯比单高斯提供更好的性能[59]，但是由于高计算需求和对有限训练数据集的过度拟合，其使用受到限制。此外，如何确定状态数对于HMM 模型配置也至关重要。基于模型的聚类算法的现有工作通常与用于参数估计的EM 算法相关联。然而，这种基于EM 的参数估计遭受局部最优和收敛困难的问题。虽然我们提出的算法提供了一个有前途的解决方案，但它在生成输入分区的集合方面非常耗时，这对于在线应用程序可能至关重要。因此，如何找到计算成本与分类精度之间的折衷方案仍然是集成技术研究的一个有趣的课题。