A unified theory of confidence intervals for high-dimensional precision matrix*

WANG Yue, LI Yang, ZHENG Zemin

(School of Management, University of Science and Technology of China, Hefei 230026, China)

Abstract Precision matrix inference is of fundamental importance nowadays in high-dimensional data analysis for measuring conditional dependence. Despite the fast growing literature, developing approaches to make simultaneous inference for precision matrix with low computational cost is still in urgent need. In this paper, we apply bootstrap-assisted procedure to conduct simultaneous inference for high-dimensional precision matrix based on the recent de-biased nodewise Lasso estimator, which does not require the irrepresentability condition and is easy to implement with low computational cost. Furthermore, we summary a unified framework to perform simultaneous confidence intervals for high-dimensional precision matrix under the sub-Gaussian case. We show that as long as some precision matrix estimation effects are satisfied, our procedure can focus on different precision matrix estimation methods which owns great flexibility. Besides, distinct from earlier Bonferroni-Holm procedure, this bootstrap method is asymptotically nonconservative. Both numerical results confirm the theoretical results and computational advantage of our method.

Keywords precision matrix; high dimensionality; bootstrap-assisted; confidence intervals; simultaneous inference; de-biased

Nowadays, high-dimensional data which are referred to as smallnlargepdata, develop extremely rapidly. Graphical models have been extensively used as a solid tool to measure conditional dependence structure between different variables, ranging from genetics, proteins and brain networks to social networks, online marketing and portfolio optimization. It is well known that the edges of Gaussian graphical model (GGM) are encoded by the corresponding entries of the precision matrix[1]. While most of the existing work concentrates on the estimation and individual inference of precision matrix, simultaneous inference methods are generally reckoned to be more useful in practical applications because of the valid reliability assurance. Therefore, it is in urgent need to develop approaches to make inference for groups of entries of the precision matrix.

Making individual inference for the precision matrix has been widely studied in the literature. Ref.[2] first advocated multiple testing for conditional dependence in GGM with false discovery rates control. It’s a pity that this method can not be applied to construct confidence intervals directly. To address this issue, based on the so-called de-biased or de-sparsified procedure, Refs.[3-4]designed to remove the bias term of the initial Lasso-type penalized estimators and achieved asymptotically normal distribution for each entry of the precision matrix. Difference lies in that Ref.[3] adopted graphical Lasso as initial Lasso-type penalized estimator but Ref.[4] focused on nodewise Lasso. They both followed the way of Refs.[5-8]which proposed de-biased steps for inference in high-dimensional linear models.

While most recent studies have focused on the individual inference in high-dimensional regime, the simultaneous inference remains largely unexplored. Refs.[9-11]creatively proposed multiplier bootstrap method. Based on the individual confidence interval, Ref.[12] proposed simultaneous confidence intervals via applying bootstrap scheme to high-dimensional linear models. Distinct from earlier Bonferroni-Holm procedure, this bootstrap method is asymptotically nonconservative because it considers the correlation among the test statistics. More recently, Ref.[13] considered combinatorial inference aiming at testing the global structure of the graph at the cost of heavy computation and only limited to the Gaussian case.

Motivated by these concerns, we develop a bootstrap-assisted procedure to conduct simultaneous inference for high-dimensional precision matrix, based on the de-biased nodewise Lasso estimator. Moreover, we summary a unified framework to perform simultaneous inference for high-dimensional precision matrix. Our method imitates Ref.[12] but generalizes bootstrap-assisted scheme to graphical models and we conclude general theory that our method is applicative as long as precision matrix estimation satisfies some common conditions. The major contributions of this paper are threefold. First of all, we develop a bootstrap-assisted procedure to conduct simultaneous inference for high-dimensional precision matrix, which is adaptive to the dimension of the concerned component and considers the dependence within the de-biased nodewise Lasso estimators while Bonferroni-Holm procedure cannot attain. Second, our method is easy to implement and enjoy nice computational efficiency without loss of accuracy. Last, we provide theoretical guarantees for constructing simultaneous confidence intervals of the precision matrix under a unified framework. We prove that our simultaneous testing procedure asymptotically achieves the preassigned significance level even when the model is sub Gaussian and the dimension is exponentially larger than sample size.

1 Methodology

1.1 Model setting

Under the graphical model framework, denote byXann×prandom design matrix withpcovariates. Assume thatXhas independent sub-Gaussian rowsX(i), that is, there exists constantKsuch that

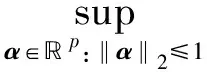
(1)

1.2 De-biased nodewise Lasso

Characterizing the distribution of Lasso-type estimator for precision matrix is difficult because Lasso-type estimator is biased due to thel1penalization. To address this problem, Refs.[3-4]adopted de-biasing idea which is to start with graphical Lasso or nodewise Lasso estimator and then remove its bias. This results in de-biased estimator generally taking the form

Then we have the following estimation error decomposition

Further we let

1.3 Simultaneous confidence intervals

(2)

(3)

c1-α,E=inf{t∈:e(WE≤t)≤1-α)}，

(4)

Remark1.1Bonferroni-Holm adjustment states that if an experimenter is testingphypotheses on a set of data, then the statistical significance level for each independent hypothesis separately is 1/ptimes what it would be if only one hypothesis were tested. However, the bootstrap uses the quantile of the multiplier bootstrap statistic to asymptotically estimate the quantile of the target statistic and takes dependence among the test statistics into account. Thus the original method with Bonferroni-Holm is on the conservative side, while the bootstrap is closer to the preassigned significance level.

1.4 A unified theory for confidence intervals

Define the parameter set

λmax(Θ)≤L,

2 Theoretical properties

Before giving the theoretical properties, we list two technical conditions.

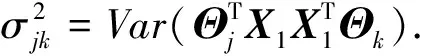
Φ(z)|=0,

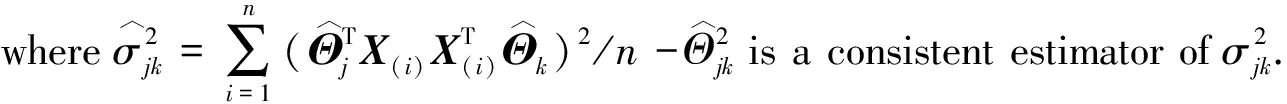
Based on the asymptotic normality properties established in Proposition 2.1, we have the following simultaneous confidence intervals for multiple entriesΘjk.

Theorem 2.1Assume that conditions (A1)-(A2) hold. Then for anyE⊆[p]×[p], we have

(1-α)|=0,

Next, we extend the above theory to more general case and conclude the unified theory for precision matrix inference.

Theorem 2.2Assume that eventHholds. Then we have

for anyE⊆[p]×[p], whereΘEdenotes the entries ofΘwith indices inE.

Next, we extend the above theory to more general case and conclude the unified theory for precision matrix inference.

Theorem 2.3Assume that eventHholds. Then we have

(A)(Individual inference)

Φ(z)|=0,

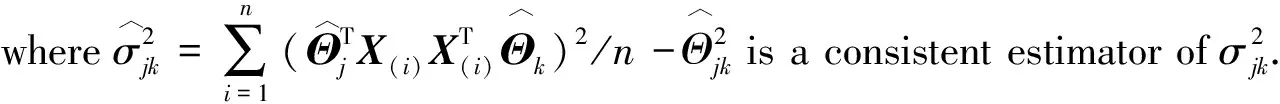
(B)(Simultaneous inference)

(1-α)|=0,

for anyE⊆[p]×[p], whereΘEdenotes the entries ofΘwith indices inE.

Theorem 2.3 presents general conclusions for both individual and simultaneous confidence intervals. That is, our inferential procedures work for any estimation methods for precision matrix as long as the estimation effect satisfies eventH.

3 Numerical studies

In this section, we investigate the finite sample performance of the methods proposed in Section 3 and provide a comparison to simultaneous confidence interval for de-biased graphical Lasso, denoted by S-NL and S-GL, respectively. We now present two numerical examples and evaluate the methods by estimated average coverage probabilities (avgcov) and average confidence interval lengths (avglen) over two cases: support setSand its complementSc. For convenience, we only consider Gaussian setting. The implementation for de-biased nodewise Lasso and de-biased graphical Lasso are suggested by Ref.[4]. Throughout the simulation, the level of significance is set atα=0.05 and the coverage probabilities and interval lengths calculated by averaging over 100 simulation runs and 500 Monte Carlo replications. For extra comparison, we also record individual confidence intervals for de-biased nodewise Lasso and de-biased graphical Lasso, denoted by I-NL and I-GL, respectively.

3.1 Numerical example 1: band structure

We start with a numerical example which has the similar setting as that in Ref.[3]. We consider the precision matrixΘwith the band structure, whereΘjj=1,Θj,j+1=Θj+1,j=ρforj=1,2,…,p-1, andzero otherwise. We sample the rows of then×pdata matrixXas i.i.d.copies from the multivariate Gaussian distributionN(0,Σ) whereΣ=Θ-1. We fix the sample sizen=100 and consider a range of dimensionalityp=300,500 and link strengthρ=0.2,0.3,0.4,0.5, respectively. The results are summarized in Table 1.

In terms of avgcov and avglen, it is clear that our proposed S-NL method outperforms other alternative methods with higher avgcov and shorter avglen in most settings. Although the avglen overScmay be a little longer in some cases, it is amazing that the coverage probabilities inSapproach the nominal coverage 95%. On the other hand, the advantage becomes more evident aspandρincrease. Compared with individual confidence intervals, simultaneous confidence intervals have longer lengths and lower coverage probabilities. This is reasonable because multiplicity adjustment damages partial accuracy which is inevitable.

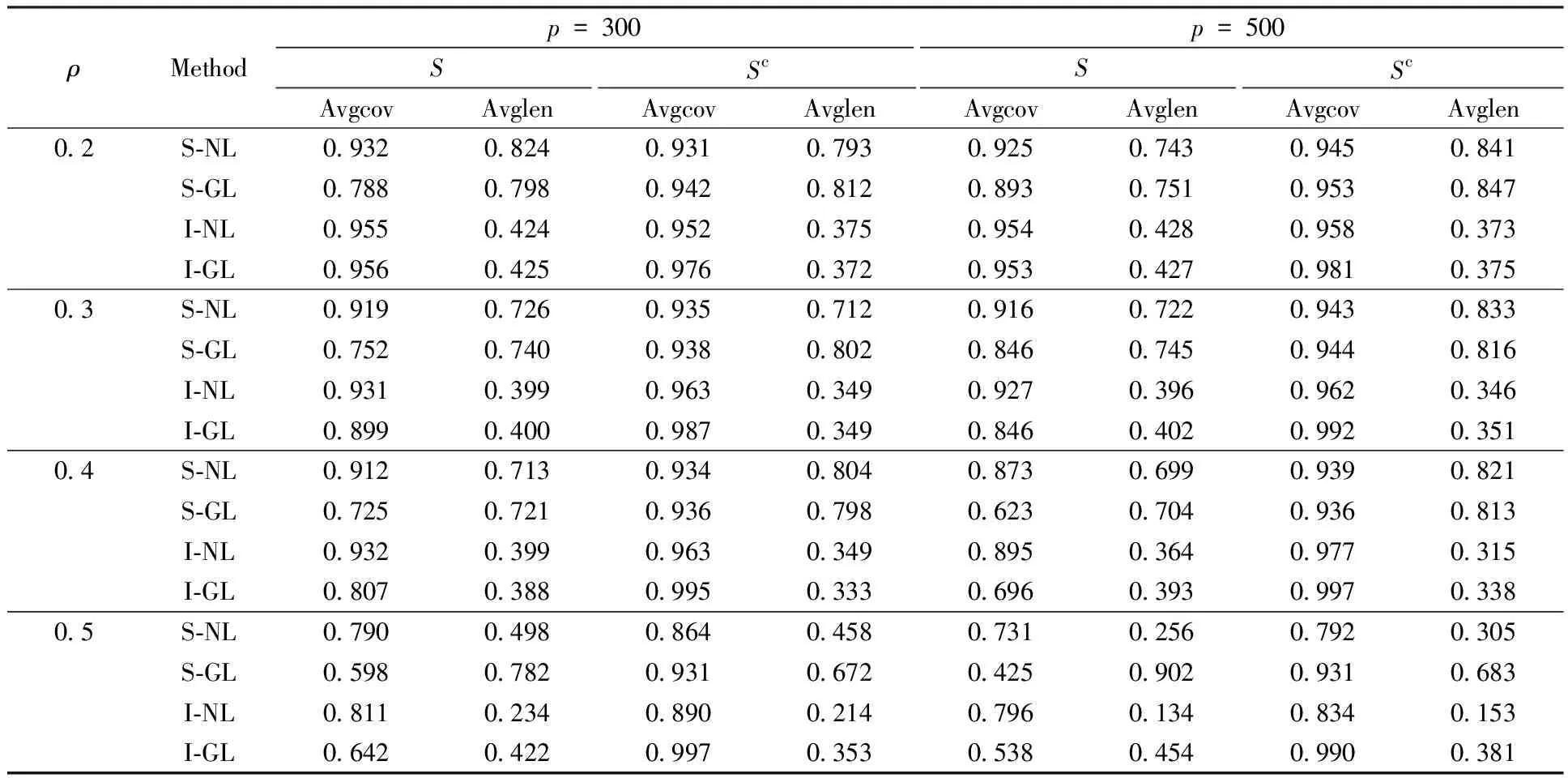
Table 1 Averaged coverage probabilities and lengths over the support set S and its complement Sc in Section 3.1

3.2 Numerical example 2: nonband structure

For the second numerical example, we use the same setup as simulation example 1 in Ref.[16] to test the performance of S-NL in more general cases. We generate the precision matrix in two steps. First, we create a band matrixΘ0the same as that in Section 3.1. Second, we randomly permute the rows and columns ofΘ0to obtain the precision matrixΘ. The final precision matrixΘno longer has the band structure. Then we sample the rows of then×pdata matrixXas i.i.d. copies from the multivariate Gaussian distributionN(0,Σ) whereΣ=Θ-1. Throughout this simulation, we fix the sample sizen=200, dimensionalityp=1 000 and consider a range ofρ=0.2,0.3,0.4,0.5.

Simulation results summarized in Table 2 also illustrate that our method can achieve the preassigned significance level asymptotically and behaves better than others in most cases. Moreover, we can see our method is very robust especially in largeρ.

4 Discussions

In this paper, we apply bootstrap-assisted procedure to make valid simultaneous inference for high-dimensional precision matrix based on the recent de-biased nodewise Lasso estimator. In addition, we summary a unified framework to perform simultaneous confidence intervals for high-dimensional precision matrix under the sub-Gaussian case. As long as some estimation effects are satisfied, our procedure can focus on different precision matrix estimation methods which owns great flexibility. Further, this method can be expended to more general settings, such as functional graphical model where the samples are consisted of functional data. We leave this problem for further investigations.

Table 2 Averaged coverage probabilities and lengths over the support set S and its complement Sc in Section 3.2

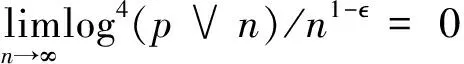
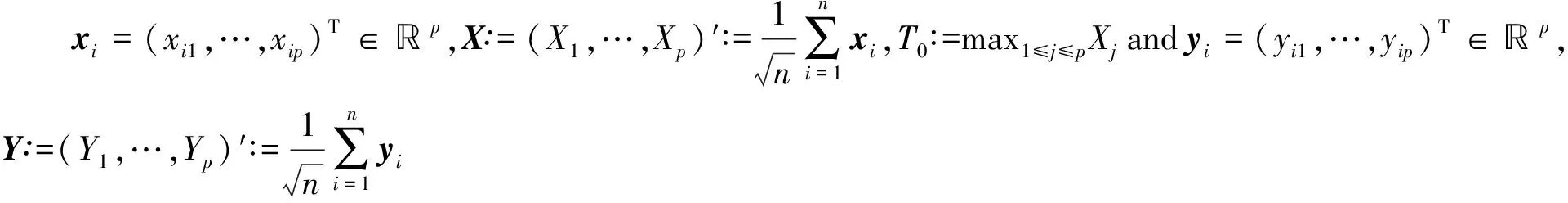
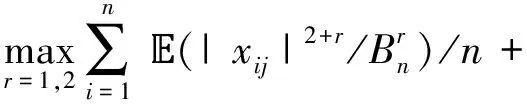
≤4,

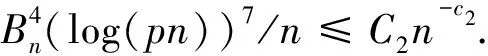
A.2 Proof of Theorem 2.1

Without loss of generality, we setE=[p]×[p]. For any (j,k)∈E, define

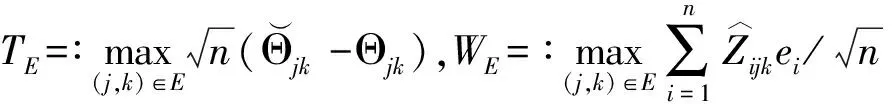
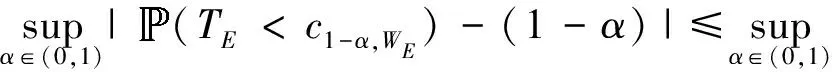
(1-α)|=0,

which conclude the proof.

A.3 Proof of Theorem 2.3

To enhance the readability, we split the proof into three steps by providing the bound on bias term, establishing asymptotic normality and verifying the variance consistency.

Step 1

∶=Z+Δ1+Δ2.

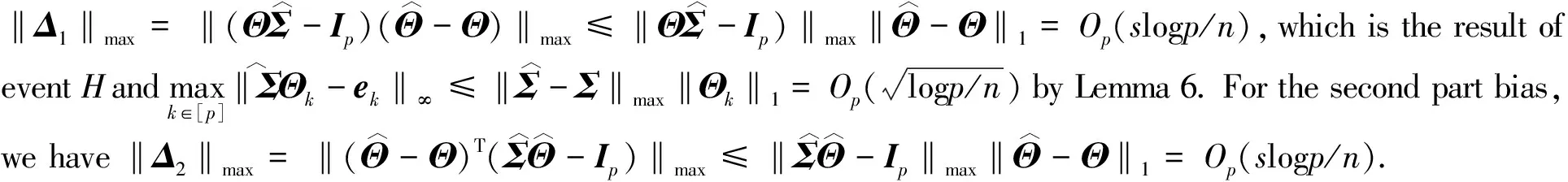
Step 2The proof is the direct conclusion of Theorem 1 of Ref.[4].

Step 3The proof is the direct conclusion of Lemma 2 of Ref.[4].

The subsequent proof is similar to Theorem 2.1, thus we omit the details.

A.4 Lemmas and their proofs

The following lemmas will be used in the proof of the main theorem.

Lemma A.1Assume that conditions (A1)-(A4) hold. Then for anyE⊆[p]×[p] we have

where {Yijk}(j,k)∈Eare Gaussian analogs of {Zijk}(j,k)∈Ein the sense of sharing the same mean and covariance fori=1,2,…,n.

ProofThe proof is based upon verifying conditions from Corollary 2.1 of Ref.[9]. To be concrete, we require to prove the following condition (E.1).

which conclude the proof.

Lemma A.2LetVandYbe centered Gaussian random vectors inpwith covariance matricesΣVandΣYrespectively. Suppose that there are some constants 00 depending only onc1andC1such that

ProofThe proof is the same as Lemma 3.1 of Ref.[9]

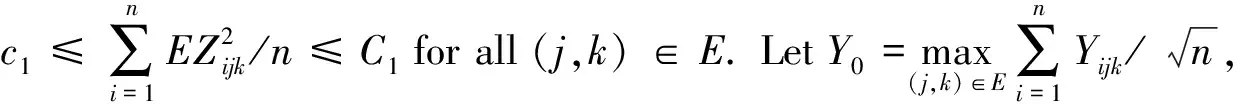
where π(ν):=C2ν1/3(1∨log(|E|/ν))2/3.

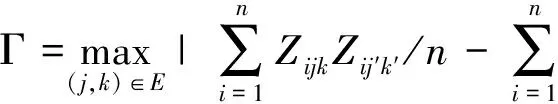
Lemma A.4Assume that conditions (A1)-(A4) hold. Then for any (j,k)∈Ewe have

Proof

Bounds for|TE-T0|: Recall that

It follows from Theorem 2.1 that

(1),

whereξ1=O(slogp/n)=o(1) andξ2=o(1).

Bounds for|WE-W0|:

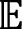
which conclude the proof.

Lemma A.5

Proof

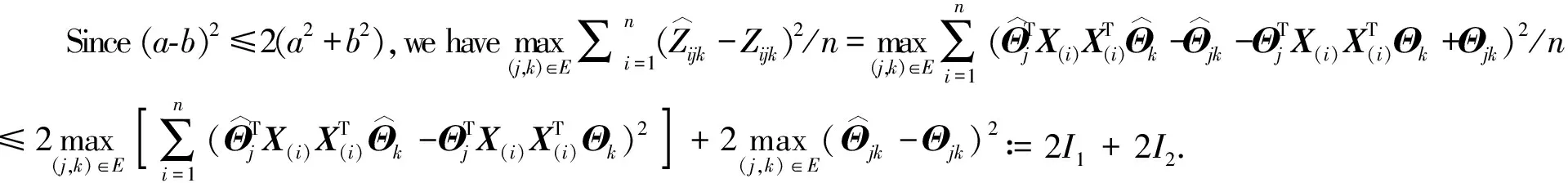
For the second part, it is obvious that

|I2|≤Op(logp/n),

which is a direct result of eventH.

Combining them together, we conclude =Op(s2logplog(np)/n)=op(1).

Lemma A.6Assume that conditions (A1)-(A4) hold. Let

ProofThe proof is the same as Lemma L.3 of Ref.[13], which follows by invoking the inequality

and Proposition 5.16 in Ref.[17] and the union bound.

Lemma A.8Letα,β∈psuch that ‖α‖2≤M,‖β‖2≤M. LetXisatisfy the sub-Gaussian setting with a positive constantK. Then for anyr≥2, we have

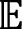
(2M2K2)r≤r!/2.

ProofThe proof is the same as Lemma 5 of Ref.[3]. Since ‖α‖2≤M,‖β‖2≤Mand sub-Gaussian assumption with a constantK, we obtain

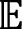
By the inequalityab≤a2/2+b2/2 (for anya,b∈) and Cauchy-Schwarz inequality we have

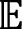
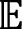
By the Taylor expansion, we have the inequality

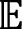
Next it follows

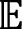
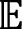
Therefore, we have