基于博弈论的散货港口堆场堆位分配算法

*

（1.武汉理工大学计算机科学与技术学院，武汉 430063；2.交通物联网技术湖北省重点实验室（武汉理工大学），武汉 430070）

0 引言

港口作为一个从事货物装卸、搬运、存储以及加工的场所，在整个运输链中扮演着关键节点的角色，是水陆交通运输的枢纽［1］。随着信息技术的迅速发展，我国港口当前正朝着更加绿色、智能的第五代港口发展［2］，并且提出了智慧港口（Smart Port）的概念［3］。例如黄骅港智能堆场系统的投运，使其成为国内散货码头自动化的标杆，专用散货煤炭码头正在实验铁路线智能排产［4］等。散货港口（特别是内河沿线港口）堆场由于面积小，件散货货类众多、形状不规则，导致作业繁杂，因此急需堆场智能分配方法来提高堆存效率和作业效率，但是和智能排产、智能调度相比，对散货码头的智能分配方面的研究目前仍处于信息搜集和处理的初步阶段［5］。因此，港口的散货堆场如何在先进技术的支持下，对堆场的货物进行智能分配，规范堆场管理，提高散货堆场的利用率成为了港口散货码头智能化研究的重点。

随着港口智能化的不断推进，堆位分配的研究不断增多，但主要还是集中在集装箱方面，针对散货港口堆场堆位分配方法的研究较少。近年来，相关学者研究堆场堆位分配问题的方法主要有系统仿真、模型和算法两类。在系统仿真方法上，Wang 等［6］研究了基于规则的煤炭堆场堆位分配问题，通过搜索可用堆场、堆位和装备三种资源来确定合适的堆存区域，建立的仿真模型能有效提高堆场的利用率，缺点是仅适用于煤炭港口。Bruglieri 等［7］基于货物体积构建混合整数规划数学模型，通过系统仿真构建3-D 堆场模型进行优化求解，并通过维多利亚港实际数据模型测试证实该模型的有效性和高效性，但它仅适用于吞吐量大、货类单一的海港。孙勇［8］建立了散货码头堆场物流系统的动态Petri 网模型，但简化了堆场物流的流程，且研究成果局限于理论。在模型和算法方面，智能算法运用广泛，Savelsbergh 等［9］通过在散货时空图上搜索空闲堆存区域、可用机械等来确定煤堆最早可以开始装卸的区域，并提出树搜索算法，能有效减少船舶等待时间，但方法适用范围有限。徐克辉［10］在建立堆场分配模型基础上，使用知识工程相关技术得到最优的堆存区域，但可用空间逐层筛选的效率还十分有限。宋昕［11］采用定性推理和定量计算相结合的方式，设计了基于本体和进化算法的散杂货港口堆场多目标优化调度算法，但在堆位匹配度计算中简化了其影响因素，需要进一步在实践中检验和完善。

博弈论主要研究多个参与者之间的理性决策问题，被广泛运用于无线网络中频谱［12］和功率分配［13］，以及云计算中“云资源”调度［14］等问题中，但针对港口的资源调度讨论较少。现有研究多针对多个竞争港口之间的定价问题。Dong 等［15］研究表明采用博弈理论的价格匹配策略能有效促进集装箱码头之间的合作。Ishii 等［16］通过实例分析得到纳什均衡解，得出多港口之间满足均衡的收费策略方案。

散货堆场是散货港口的核心资源，堆位分配是堆场资源调度中极为重要的部分。散货堆场堆位分配是一个复杂的综合性问题，不仅需要考虑堆场的占用情况，还需考虑装卸船的作业效率。港口（特别是散货港口）货物进港有一定的不确定性。由于卸船作业在船舶剩余货物量多时机械作业效率较高，因此在货源充足的情况下，为提高效率，港口会将一船货物分批卸入，在作业繁忙时优先作业剩余货物较多的船舶，较空闲时再作业剩余货物量少的效率低的部分。由于所有作业的货物都需要进入堆场，因此堆位分配时既要统筹全局，也要局部关注货物和堆位的匹配度。如何协调多票货物的分配以达到某种均衡状态，是堆位分配需要解决的问题。

当前，港口向着智能化方向不断发展，但对于散货港口堆场堆位分配的研究仍非常有限，因此，为综合考虑堆场资源的合理化利用和装卸作业进度的匹配程度，本文采用博弈论的思想，通过设定博弈策略，进行多次迭代博弈，采用“满足均衡”［17］分析博弈，以寻求使得堆位分配达到均衡的分配方案，从而提高货物与堆位之间的匹配度，提高堆场使用效率，降低不必要的作业成本。

1 港口散货堆场堆位分配模型

散货堆场堆位分配模型用来描述多票货物博弈的堆位分配情况，通过设计博弈策略和相应的博弈算法，使得复杂的散货堆场的堆位分配结果达到一种均衡状态。

1.1 模型要素

堆位分配模型包括港口堆场相关资源的描述，以及博弈论中三大基本元素，即参与者、策略空间和效用函数。

1.1.1 堆场资源描述

建立一个堆场形式化模型是进行堆位分配的基础，模型对相应的资源及条件进行符号化描述，本文采用如下一种四元组的形式来描述堆场模型Y=其中：S={si|i=1，2，…，k1}，si表示第i个堆位，每一个堆位包含其基本信息如容量、所在位置和支持存储货类等；H表示堆场目前堆存的货物，H={hi|i=1，2，…，k2}，hi表示第i票货物，其中包含货主、货类、重量等基本信息；J表示堆场作业机械（堆取料机）集合，J={ji|i=1，2，…，k3}，ji表示第i个机械，每个机械包含所处位置等信息；R代表堆场的作业线集合，R={ri|i=1，2，…，k4}，ri表示第i条作业线，每条作业线包括配置人员数量、每个环节工作量系数（作业单价）等信息。

1.1.2 参与者

在堆场堆位分配的博弈模型中，参与者为当前时刻确定的即将卸货入堆场的多票货物，用集合N={Ni|i=1，2，…，n}表示，∀Ni∈N都包含以下相关属性：货主、货类、重量、进出港运输方式等。

1.1.3 策略空间

针对当前的堆场Y，需要搜索出所有可用的堆位，集合S={s1，s2，…，sM}表示有M个可用堆位，将参与者做出决策（选择某一堆位）这一动作称为行动（action），定义ai表示参与者i的行动，所有的行动集合称为行动空间（action space），即策略空间。用Ai表示参与者i的行动空间，Ai={s1，s2，…，sK}，K≤M，即有Ai⊆S。参与者i根据博弈的混合策略原则从Ai中选择行动，即遵循特定的概率分布πi=其中表示参与者选择行动sk的概率，即第i票货物选择可用堆位k的概率。

1.1.4 效用函数

堆位具有诸多属性，比如支持存放的货类、堆位的容量、是否靠近铁路线或码头等，每个属性都可以量化为相应的属性值，同时，货物对堆位的各个属性具有一定程度的偏好，比如采用船舶运输的货物对靠近码头的堆位有着较重的偏好。同样可以量化为偏好值。将上述属性和偏好处理为向量，称为属性向量和偏好向量。假设抽取出T个因素，有pi=[pi1，pi2，…，piT]表示第i个堆位的属性向量，pij，j∈(1，2，…，T)表示堆位i在属性j上的属性值。同样有ri=[ri1，ri2…，riT]表示货物i的偏好向量，rij，j∈(1，2，…，T)表示货物i对堆位属性j的偏好度。设rmax=pmax为货物偏好值和堆位属性值的上限，规定0 ≤pij≤rmax=pmax。

在属性向量和偏好向量的基础上，为每个参与者定义函数gi：pi→[0，1]来度量分配的匹配度，如式（1）所示：

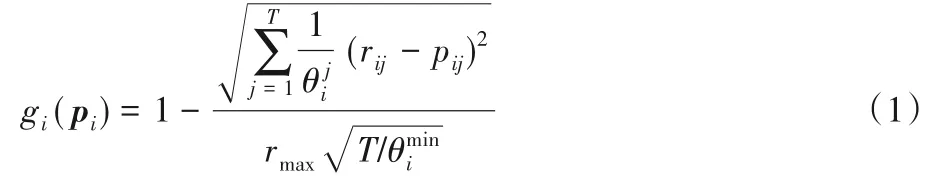
1.2 散货堆场堆位分配中动态博弈的表现

本文建立的堆位分配模型中博弈的动态性具体表现在参与者的博弈次序和策略空间上。

1.2.1 博弈次序

根据参与者做出决策的顺序将博弈分为静态博弈和动态博弈。本文博弈模型的参与者为待分配的货物，港口通过相应的卸货计划获得需要的卸货信息，由于港口作业具有较大的不确定性，卸货计划在一定时间段内并不确定，因此参与者的信息具有动态的特性。同时，由于各参与者对堆位资源是独占的、不可共享的，因此在博弈分配的过程中需要维持一定的顺序以推进博弈的进行。初始的博弈顺序可采取卸货计划到达的先后顺序。

1.2.2 策略空间的动态变化

为了避免为每一个参与者都维系一个策略空间所带来的琐繁，规定所有的参与者共享同一个策略空间，即所有货物都可以分配到可用的堆位，可以通过概率分布πi进行控制，例如前面的货物i选择堆位j后，那么后面的参与者概率分布中=0。同时，若货物i在做出选择后，后面存在参与者k的货类不能与货物i相邻，因此对于参与者k而言，所有货物i相邻的可用堆位的选择概率均为0。

策略空间动态变化只发生在一次博弈过程中，在下一次博弈时，策略空间需要恢复到初始状态。

1.3 散货堆场堆位分配的满足博弈

在动态博弈中，由于参与者之间存在着竞争对抗的关系，从而导致收益无法达到最大化。本文将满足均衡［17］的概念运用在堆位分配中，解决纳什均衡［17］难以分析的问题。

1.3.1 满足式表述

假设参与者对收益有一个低于最优值Γmax的预期，设为Γ，若存在行动组合s=(si，s-i)使得ui(s) ≥Γi，其中si，s-i分别表示参与者i的策略组合和除i之外其他参与者的策略组合。则称参与者i达到满足状态。定义映射如下：

将其表示为式（2）所示的形式：

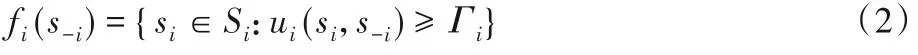
因此可用式（3）所示的三元组表示博弈模型，称为博弈的满足式表达：

其中：N为参与者，Si为策略空间。

1.3.2 满足均衡

满足均衡（Satisfaction Equilibrium）指的是与上述1.3.1节中满足式（3）表述所对应的均衡，如定义1。

定义1若给定行动s*=针对式（3）所示的满足式表述，有∀i∈N→则称s*为博弈的满足均衡［17］。

1.3.3 满足博弈

若不考虑货物之间对堆位的竞争关系，则货物i在其策略空间的最大效用为其理想效用，定义货物i理想效用如式（4）所示：

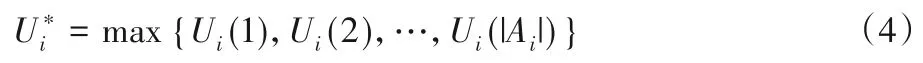
其中：Ui=gi，根据满足均衡的定义，若给定一个行动ai，即分配堆位j，其属性向量pj，若有ui(ai，a-i)=gi(pj)≥Γi，则称货物i得到满足。本文建立的基于博弈论的散货堆场堆位分配模型可用式（5）所示的三元组表示。

效用函数量化了堆位分配的质量，但各票货物对分配的质量要求不同，通过期望效用表示这种要求，为了体现每一次的分配在这种要求下的效果，本文定义满足度来表示。

定义2货物在某一堆位处的效用与期望效用之比称为满足度，记作：

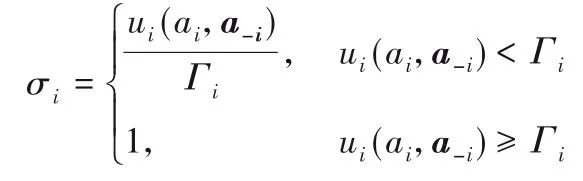
其中，σi表示货物i的满足度，用σ-i表示其他货物的满足度，即：

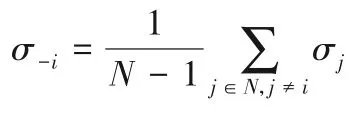
引入σi和σ-i之后，可以将ui(ai，a-i) 改写为ui(σi，σ-i；ri)，函数ui(·；ri)以ri作为参数，以σi和σ-i作为输入变量。

1.4 装卸成本函数

不同的堆存区域对货物的装卸成本有着直接的影响，且各货物有着其成本上限，因此在堆位的分配过程中，需要考虑其装卸成本。定义Cji表示第i票货物分配堆位j所产生的装卸成本，如式（6）所示：

为了直观地体现装卸成本，仅考虑港方在装卸过程中的金钱成本，同时作业线每个环节的工作量系数（作业单价）已经事先设置好，因此成本计算包括两个方面：机械成本和人员成本。假设所有作业线包含S个环节，M种机械，每个环节的人力成本单价为ps(s=1，2，…，S)（元/吨）。机械成本仅考虑其机械本身在作业过程中的油耗和损耗成本两部分，并通过实际生产中机械的维护数据可以计算出相应机械的油耗oilm和损耗系数losm（元/吨）。以卸货成本为例，计算如式（7）所示：

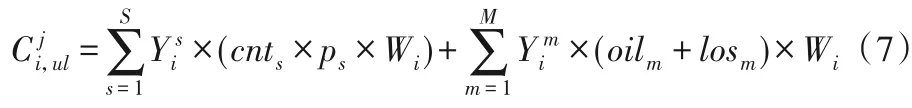
1.5 模型求解目标

1）堆位分配目标。

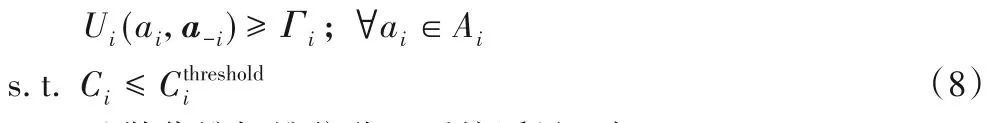
2）散货堆场堆位分配系统诱导目标。

散货堆场堆位分配系统的诱导目标主要有：①使得所有货物的效益和最大，如式（9）所示；②使得所有货物的装卸成本和最小，如式（10）所示：

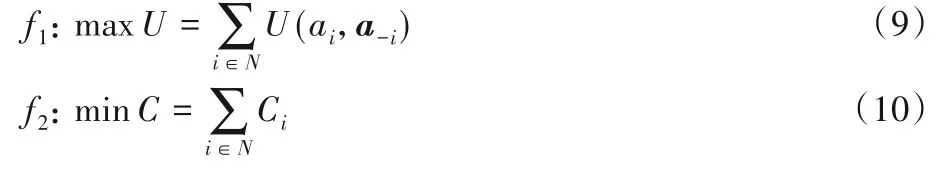
为了更好地衡量堆位分配的效果，本文定义堆场分配效益，堆场分配效益为以上两者的线性组合，如定义3所示。

定义3设ωU，ωC分别表示货物分配效用、装卸成本的权值系数，两者之和为1，所有货物分配的效用值以及装卸成本的带权和称为堆场分配效益，如式（11）所示：

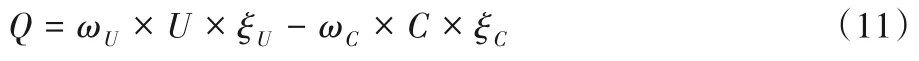
其中：ξU、ξC分别表示将货物分配效用值和装卸成本转化为堆场效益的正参数，是在具体港口的实际情况下，根据货物效用和装卸成本计算结果的动态变化范围以及数量级关系来设置相应部分转为堆场使用效益的正参数，其值可通过实验和实际生产数据统计分析得到。相应的权值系数取值范围均为［0，1］。如果忽略装卸成本，所得效益称为理想堆场分配效益。

定义4堆场所有货物的理想效用的累加和称为理想堆场分配效益，如式（12）所示：

显然，任何阶段的堆场分配效益都小于理想堆场分配效益，Qt表示博弈阶段的堆场分配效益，则有Qt＜Q*。

散货堆场堆位分配系统的诱导目标为最大化堆场分配效益，如式（13）所示：

本文旨在找到某一分配组合a+，使其成为式（8）、（13）最优解，称a+为系统均衡解，即本文建立的分配模型求解目标为：在提高货物与堆位匹配度的同时最大化堆场分配效益。

2 港口散货堆场堆位分配模型求解

2.1 博弈次序调整策略

博弈次序决定参与者做出决策的顺序，为了体现堆位分配中的公平性和加速堆位分配算法的收敛，本文采取如下规则调整博弈次序。

1）初始博弈次序采用系统卸货计划顺序，即先来先服务。

2）假设货物i在第t-1 次迭代中获得效用与期望效用的距离记作＜0 时，效用未达到预期≥0时，效用已达预期。

2.2 堆位分配策略

堆位分配采取迭代的思想，每一次迭代开始的输入和输出形式如下：

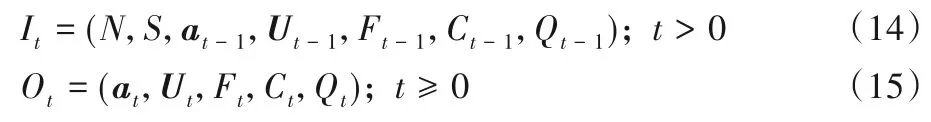
输入为所有的参与者信息N（所有待分配的货物），初始的策略空间S（可用的堆位集合），前一次的迭代分配结果at-1，前一次的效用向量Ut-1，前一次的总装卸成本Ct-1，前一次的堆场分配效益Qt-1，同样输出为本次迭代的相应结果。根据文献［17］，本文规定迭代过程按如下规则进行：

1）初始分配。

初始的博弈次序采用卸货计划的顺序，即先来先服务。

初始时刻（t=0），货物i对策略空间进行搜索，过滤掉已被占用的堆位，得到可用策略空间并计算其在行动空间上的概率分布，然后选择ai(0)，货物选择行动ai(0)的概率计算如式（16）所示：

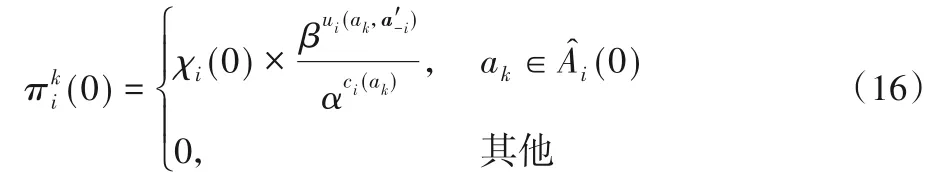
其中：ci(ak)表示选择该行动的装卸成本，α(α＞1)表示货物对装卸成本的重视程度，α取值越大，货物在分配堆位过程中越重视装卸成本；β(β＞1)表示货物对效用的重视程度，β取值越大，表示越重视货物分配所取得的效用。表示在当前局面中其他货物的分配结果向量，χi(0)为归一化因子，按式（17）计算：

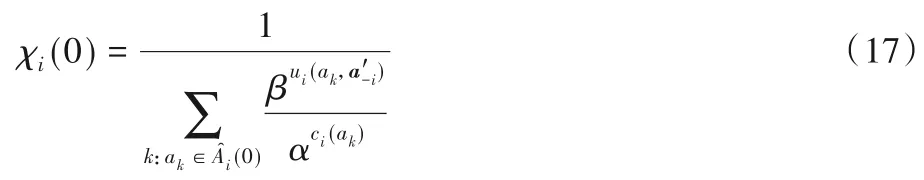
初始时刻，由于没有历史选择策略可供参考，理性的参与者以效用最大且成本最小的方式选择堆位。

2）迭代分配过程。

在第t次迭代开始时(t=1，2…)，货物i首先判断目前的分配ai(t-1)是否满足了预期，即效用和装卸成本是否满足要求。定义指示变量νi(t-1)，计算如式（18）所示。

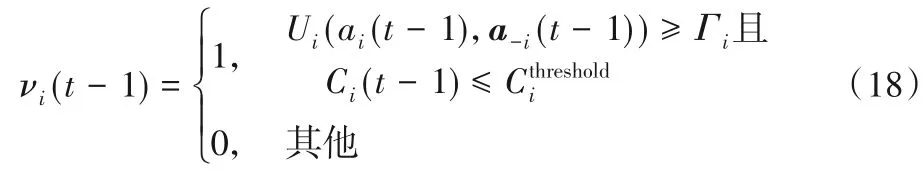
在第t次迭代过程中，货物根据νi(t-1)的取值更新概率分布，然后选择行动ai(t)。需要说明的是，受动态博弈的博弈次序影响，在新的迭代中，前一次分配的堆位可能不可用。因此，在指示变量为0或者1时都需要考虑ai(t-1)是否可用问题。当然这是很容易判断的，根据前面参与者的决策和策略空间的动态变化得到当前策略空间新一轮迭代按照如下规则进行。

如果当前货物i还未达到预期，即νi(t-1)=0，此时，货物i可能改变策略，或其他货物改变策略。但是其他货物的行动策略不确定，作为理性的参与者，希望此时的选择在将来看来是不后悔的，此时的行动选择概率如式（19）所示：

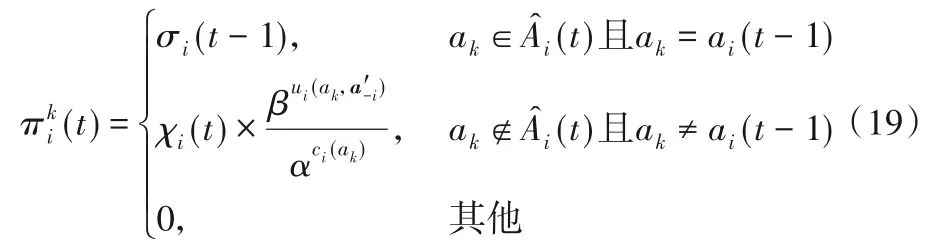
其中，σi(t-1)表示货物i对前一次分配的不后悔程度。对前一次迭代的选择越不后悔，那么继续选择该堆位的概率就越大；即在新的一次迭代中继续保持上一次的分配结果。不后悔程度可直接用满足度表示，具体表现形式如式（20）所示：

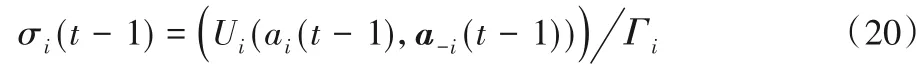
从式（20）中可以看出，若上一次分配获得的效用越接近于预期效用，σi(t-1)取值越大，则货物保持前一次选择的概率越大。因此随着迭代的进行，货物的效用逐渐接近预期效用，则不再改变策略，达到均衡状态。归一化因子χi(t)定义如式（21）所示：

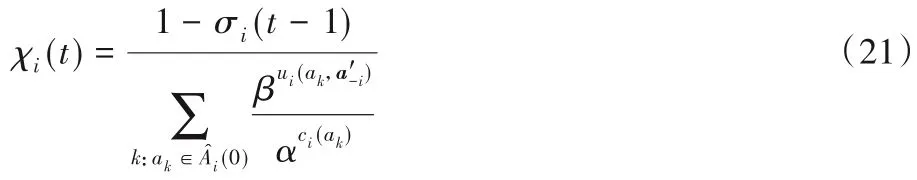
如果前一次的分配已经达到预期，即σi(t-1)=1，则货物i很有可能不改变策略，此时，概率的计算方式如式（22）所示：

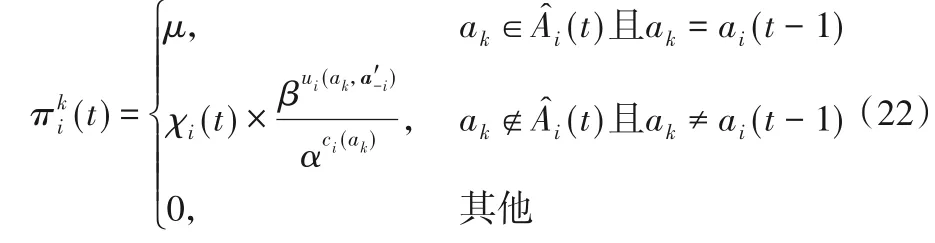
其中：参数μ表示货物维持前一次选择的概率，文献［17］证明0.5 ≤μ≤1，此时归一化因子χi(t)计算如式（23）所示：

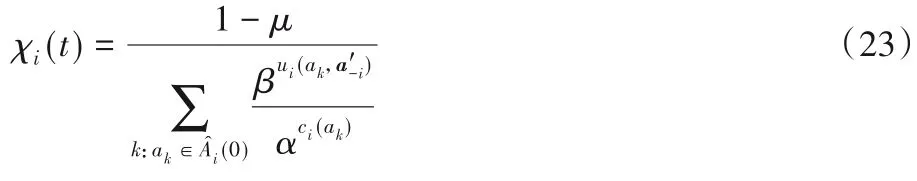
当所有货物都分配了堆位之后，按照式（17）输出结果，之后进入下一次迭代。

3）算法结束。

若经过ts(ts＞0)次迭代之后，所有的货物都得到了满足，或者算法迭代达到最大可接受次数tmax，算法终止并按式（15）输出最佳分配组合。

2.3 基于博弈论的散货堆场堆位分配算法

本文根据上述堆位分配策略提出基于博弈论的散货堆场堆位分配算法，主要由两部分组成：1）算法初始阶段为每票货物根据贪心策略分配堆位；2）随后按照上述博弈策略进行多次的迭代分配直到算法满足终止条件。该算法的流程如图1所示。

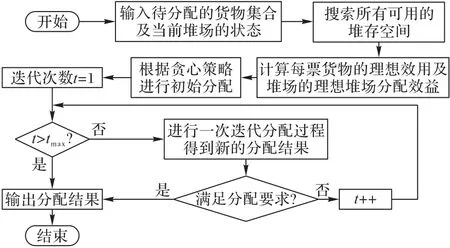
图1 基于博弈论的散货堆场堆位分配算法Fig.1 Bulk storage assignment algorithm in bulk port based on game theory

2.4 算法收敛性证明

这里采用数学归纳法证明基于博弈论的散货堆场堆位分配算法（Bulk Storage Assignment Algorithm in Bulk port based on Game theory，BSAABG）可使堆场分配效益随着算法迭代次数的增加而增大，最后达到收敛。

初始分配阶段，各货物根据贪心策略分配，此时堆场分配效益有Q0＜Q*，对应的分配结果为a0。在迭代阶段有如下几种情况：

1）第1次迭代。

根据初始的分配结果Q0和博弈次序调整策略对所有货物N进行重新排序，对∀i∈N按照分配策略进行分配。

①对于第1 票货物（通常将船上装载的某一规格货物称为1票货，一般每艘船载货数少于5票）：

分配初始阶段，使用a0中第1票货物的分配结果a0，1作为初始的分配结果，此时堆场的最优分配效益为Q0。记Q1，1，0=Q0。Q1，1，0表示第一次迭代，第一票货物做出决策后堆场分配效率。

更新第1 票货物对应策略空间的概率分布，选出所有使得效用得到满足的行动，设有K1，1个行动使得效用达到满足。货物试探性地选取K1，1中每一个行动j，并计算其堆场分配效率Q1，1，j。从中选取最大的堆场分配效益Q1，1=max{Q1，1，0，Q1，1，1，…，Q1，1，j，…，Q1，1，K1，1}，对应的行动为a1，1。此时有Q0=Q1，1，0≤Q1，1≤Q*。

②对于第i+1票货物（2 ≤i+1 ≤|N|）：

设第i票货物做出决策后，所得堆场分配效益为Q1，i。

分配初始阶段，使用a0中第i+1 票货物的分配结果a0，i+1作为初始的分配结果。由于前i票货物已经确定行动，当前局面的最优堆场分配效益为Q1，i。记Q1，i+1，0=Q1，i。

更新第i+1票货物对应策略空间的概率分布，选出所有使得效用得到满足的行动，设有K1，i+1个行动使得效用达到满足。货物试探性地选取K1，i+1中的每一个行动j，并计算出堆场分配效率为Q1，i+1，j，然后，从中选取出其最大的堆场分配效益为Q1，i+1=max{Q1，i+1，0，Q1，i+1，1，…，Q1，i+1，j，…，Q1，i+1，K1，1}，对应的行动为a1，i+1。此时有Q1，i=Q1，i+1，0≤Q1，i+1≤Q*。

综上，第1次迭代中各票货物通过试探性分配所得堆场分配效益间关系为Q0≤Q1，1≤…≤Q1，i+1≤…≤Q1，|N|≤Q*。第1次迭代所得的分配结果为a1，堆场分配效益为Q1，满足Q0≤Q1≤Q*。

2）第t+1次迭代。

设第t次迭代后得到的堆场分配效益为Qt，对应的分配结果为at。

①对于第1票货物：

分配初始阶段，使用at中第1 票货物的分配结果at，1作为初始的分配结果，此时堆场的最优分配效益为Qt。记Qt+1，1，0=Qt。

更新第1票货物对应策略空间的概率分布，选出所有使得效用得到满足的行动，设有Kt+1，1个行动使得效用达到满足。货物试探性地选取Kt+1，1中的每一个行动j，并计算其堆场分配效率Qt+1，1，j。然后，从中选取出其最大的堆场分配效益为Qt+1，1=max{Qt+1，1，0，Qt+1，1，1，…，Qt+1，1，j，…，Qt+1，1，K1，1}，对应的行动为at+1，1。此时有Qt=Qt+1，1，0≤Qt+1，1≤Q*。

②对于第i+1票货物（2 ≤i+1 ≤|N|）：

设第i票货物做出决策后，所得堆场分配效益为Qt+1，i。

分配初始阶段，使用at中第i+1 票货物的分配结果at+1，i+1作为初始的分配结果。由于前i票货物已经确定行动，当前局面的最优堆场分配效益为Qt，i。记Qt+1，i+1，0=Qt，i。

更新第i+1 票货物对应策略空间的概率分布，选出所有使得效用得到满足的行动，设有Kt+1，i+1个行动使得效用达到满足。货物试探性地选取Kt+1，i+1中每一个行动j，并计算堆场分配效率Qt+1，i+1，j。然后，从中选取出最大堆场分配效益Qt+1，i+1=max{Qt+1，i+1，0，Qt+1，i+1，1，…，Qt+1，i+1，j，…，Qt+1，i+1，K1，1}，对应的行动为at+1，i+1。此时有Qt，i=Qt+1，i+1，0≤Qt+1，i+1≤Q*。

综上，第t+1 次迭代中，各票货物通过试探性分配所得到的堆场分配效益的关系为Qt≤Qt+1，1≤…≤Qt+1，i+1≤…≤Qt+1，|N|≤Q*。第t+1 次迭代所得的分配结果为at+1，堆场分配效益为Qt+1，满足Qt≤Qt+1≤Q*。

由上述分析可得Q0≤Q1≤…≤Qt≤…≤Q*，即随着迭代次数的增大堆场分配效益也逐渐增大，最后达到收敛。

2.5 时间复杂度分析

根据算法的时间复杂度分析方法，对本文算法的时间复杂度进行分析。本文的散货堆场堆位分配方法分为初始分配和迭代分配：1）初始分配阶段，各票货物按照先来先服务的原则，根据贪心策略选择堆位，设有待分配的货物为N，可用堆位数为M，计算选择堆位的概率分布，因此初始分配阶段的时间复杂度为O(NM)。2）迭代分配阶段，首先需要调整博弈次序，进行从小到大排序，时间复杂度为O(NlogN)，然后对每票货物进行策略调整，首先计算随机概率分布，然后试探性地选择满足效用的堆位，故时间复杂度为O(NM2)，综上，本文所提的堆位分配算法时间复杂度为O(NlogN+NM2)。

3 实验结果与分析

3.1 实验平台

本文实验所依托的软硬件环境如下：处理器为Intel（R）Core i5-6360U CPU 2.0 GHz；内存为8 GB 1867 MHz LPDDR3；操作系统为Windows 10 专业版；开发语言为Java 1.8.0_111；开发工具为IntelliJ IDEA 2018.2.6；服务器为Tomcat 8.8.50；工具包为SpringMVC5.2.1.RELEASE、Hibernate 5.1.0.Final；数据库为Oracle 12。

3.2 实验数据

本文实验所使用的数据均来自某内河散货港口，主要包括堆场基础数据和生产业务数据。

3.2.1 堆场基础数据

基于本文模型的假设条件，使用的堆场布局如图2 所示，取该港口的两个大型散货堆场，编号A、B，4 台堆取料机。堆场共划分为六个区块，编号规则见图2。其中堆场A的长度为420 m，区块宽度为50 m；堆场B 的长度为200 m，区块宽度为40 m。

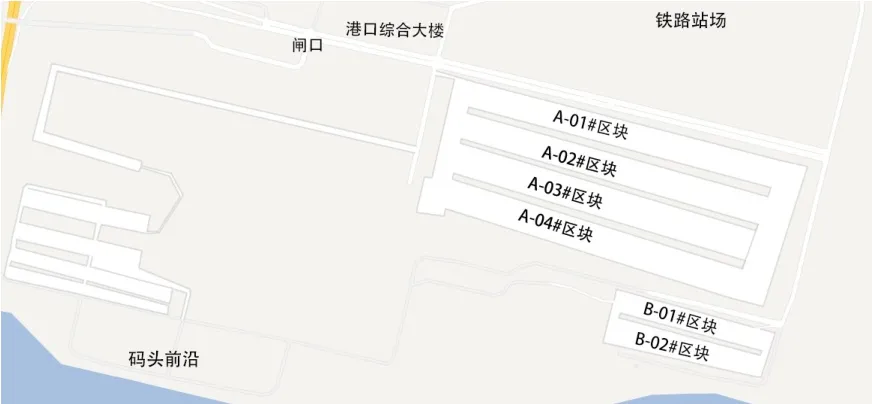
图2 某内河港口真实堆场实况图Fig.2 Live map of a real storage yard in an inland port

3.2.2 生产业务数据

生产业务数据主要为卸货计划信息，即参与者的信息，从该港口的生产业务管理系统数据库中获取，如图3所示。

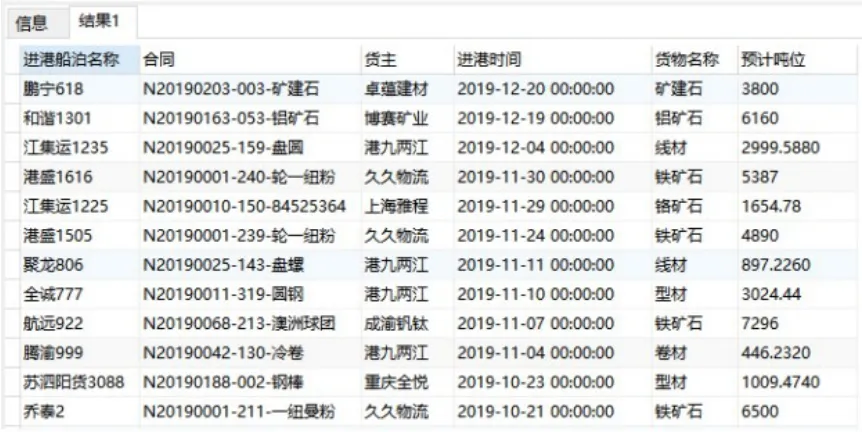
图3 生产业务数据采集示例Fig.3 Production business data collection example

3.2.3 性能指标

为了评估基于博弈论的散货堆场堆位分配算法的可行性和有效性，根据本文设计思想，选择货物的平均满足度和堆场分配效益作为算法的性能指标，如式（24）、（25）所示：

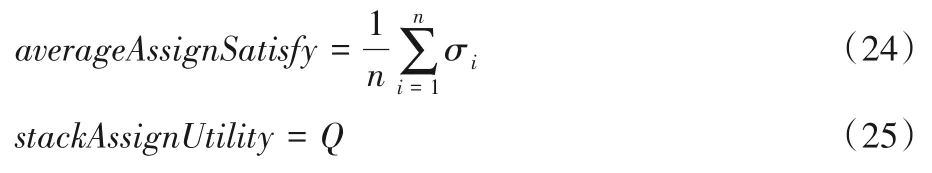
3.3 实验验证及分析

为了将本文提出的基于博弈论的散货堆场堆位分配算法（BSAABG）与目前普遍采用的人工调度经验进行比较，在同一组实验数据上，邀请重庆某散货港口两名调度员依据其调度经验进行模拟分配，将模拟分配结果和贪心算法（Greedy Algorithm，GA）所得结果进行比较发现：当货物数量较大时，由于堆场作业的复杂性，调度人员此时无法掌握堆场全局，只能考虑到某一局部状态，此时和贪心算法的求解思想一致，所以两者分配结果所获得的堆场使用效益相近。因此用贪心算法模拟人工调度经验是可行的，将人工分配过程模拟为贪心算法，按照先来先服务的次序，为货物分配堆位。文献［6，10］通过制定相应的分配规则，设计基于规则的堆位分配算法（Storage Assignment algorithm Based on Rule，SABR），算法设计堆位分配的状态空间，通过可用机械、可用堆存区和堆位匹配度进行状态空间筛选，得到分配结果。本文对以上三者进行实验对比分析。

3.3.1 博弈次序调整中阈值ξ的确定

博弈次序的调整直接影响着算法的迭代收敛，博弈次序调整的关键在于阈值ξ的设定，本文设定参与者数量为5、10、15、20，对每组实验进行20 次迭代，观察的变化情况，结果如图4所示。

ξ的变化情况反映了在迭代过程中堆场分配效益Qt-1向理想堆场分配效益Q*收敛的情况。随着迭代的进行，堆场分配效益增大，ξ值减小。当货物数量较少时，算法收敛整体平稳，当货物数量增加时，算法后期会有波动。结合实验结果和现场作业特点，本文以10 票货物为界限，当货物数量N≤10时，货物数较少，为了得到更好的效益，ξ可适当减小，取值0.18；当N＞10 时，为了避免算法震荡，无法收敛，ξ可适当增大，取值0.35。

为了评估同时请求堆位分配的货物数量对实验结果的影响，本实验将货物数量n设置为4、8、12、16、20，其中每组实验数据采用10次重复实验结果的平均值。

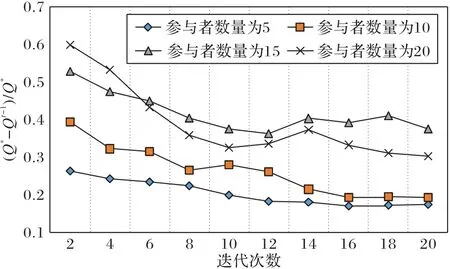
图4 (Q*- Qt -1)Q*随迭代次数变化情况Fig.4 (Q*- Qt -1)Q*changes with the number of iterations

3.3.2 参数设置

根据该内河港口的实际作业情况，对本文相关参数进行设置和调整，下面给出部分参数的取值分析。统计分析该港口单日堆场装卸作业数据可知，单日同时卸货总票数不超过20，所以确定本文货物数量n的取值范围为［1，20］，算法最大迭代次数tmax和n的取值相关，若货物数量增加，可适当增大tmax，本文根据港口实际作业情况设tmax取值20。港方在卸货时的投入往往比装货时大，因此在装卸成本计算式（6）中，卸货权重略大于装货权重。根据港口实际作业情况的货物效用和装卸成本计算结果动态变化范围以及数量级关系，设置相应部分转为堆场分配效益正参数。博弈次序调整策略阈值在3.2.1节中已经确定，文献［17］已证明0.5 ≤μ≤1，具体相关参数设置如表1 所示，参数设置应结合港口具体情况，可根据历史数据和观察实验结果进行动态调整。

表1 实验参数设置Tab.1 Experimental parameter setting

3.3.3 货物数量对货物平均满足度的影响

如图5 所示，贪心算法、SABR 和本文算法中货物的平均满足度随着货物数量增加呈现出下降的趋势。随着同时请求堆位分配的货物数量增加，货物之间的竞争加剧，无法最大化每一票货物的效用，导致满足度无法均衡，整体平均满足度下降。当货物数量为8 时，本文算法的平均满足度比贪心算法提高7.2%，比SABR 算法提高3.4%。当货物数量为20时，本文算法的平均满足度比贪心算法提高了62.5%，比SABR 算法提高了18.2%。总体而言，随着货物数量的增加，本文算法比贪心算法和SABR 算法更能够提高货物的平均满足度。原因是贪心算法忽视了货物之间对堆位的竞争关系，SABR算法在搜索过程中没有考虑装卸成本等因素，而本文的分配算法在考虑堆位匹配度和装卸成本的同时，通过迭代进行货物之间的博弈，使整体效用得到均衡。

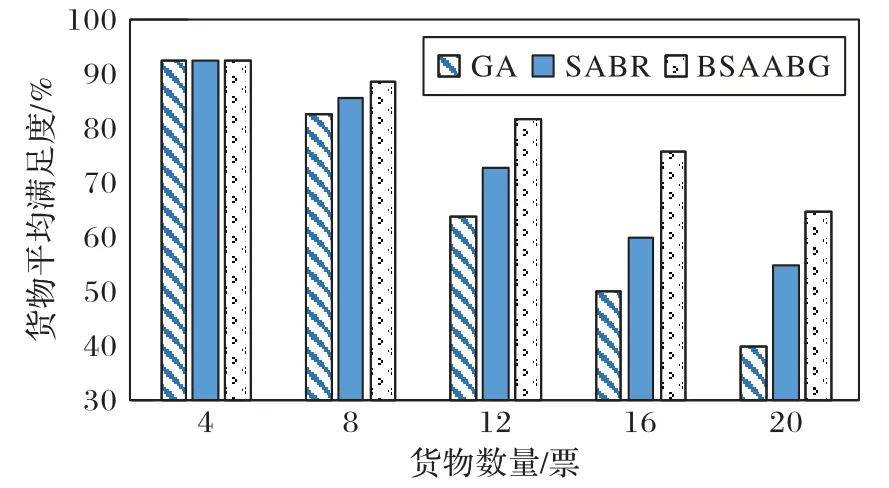
图5 货物数量对货物平均满足度的影响Fig.5 Effect of cargo quantity on the average satisfaction

3.3.4 货物数量对堆场分配效益的影响

如图6 所示，贪心算法、SABR 算法和本文算法中堆场分配效益随着货物数量的增加呈现出下降趋势。原因是随着请求堆位货物数量的增加，平均满足度降低且装卸成本增加，因此堆场分配效益降低。当请求堆位的货物数量为4 时，本文算法的堆场分配效益是贪心算法的1.1 倍，是SABR 算法的1.05倍。当请求堆位的货物数量为20时，本文算法中的堆场分配效益是贪心算法的6.83 倍，是SABR 算法的3.22 倍。综上可知，在货物数量增大的情况下，本文算法相较于贪心算法和SABR 算法能更好地提高堆场分配效益。原因是贪心算法和SABR 算法分配时只考虑单票货物本身和堆位的匹配度，缺乏对堆场整体效益的考虑。而本文算法在迭代过程中通过调整分配策略，使得分配效益增大，即增大堆场分配效益。

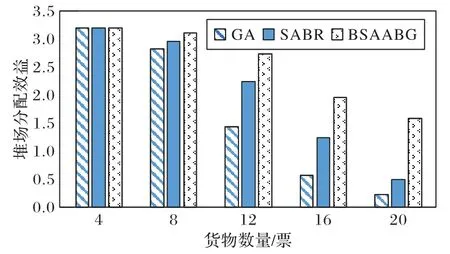
图6 货物数量对堆场分配效益的影响Fig.6 Effect of cargo quantity on distribution benefit

3.3.5 货物数量对算法执行时间的影响

如图7 所示，贪心算法、SABR 算法和本文算法的运行时间随着请求堆位货物数的增加而呈现上升的趋势。在算法执行时间上，无论货物数量的多少，前两个算法的执行时间均低于本文算法。当货物数量为4 时，贪心算法的执行时间仅为1.252 s，而本文算法执行时间为3.272 s。当货物数量为20时，贪心算法的执行时间仅为2.485 s，而本文算法执行时间为8.902 s。原因是贪心算法和SABR算法的实现逻辑相对简单，是对单票货物的操作，而本文算法由于进行迭代操作，时间复杂度较大。港口进行堆位分配从需求上而言，对实时性要求并不高，以极少的时间代价换取货物和堆位匹配度的提升和提高堆场的效益是值得的。

综上，在散货堆场中，当同时请求堆位分配的货物数量较多时，本文算法与贪心算法和SABR 算法相比，能够提高货物的平均满足度和堆场分配效益。虽然本文算法的执行时间较长，但结合实际，尚在可接受范围内。

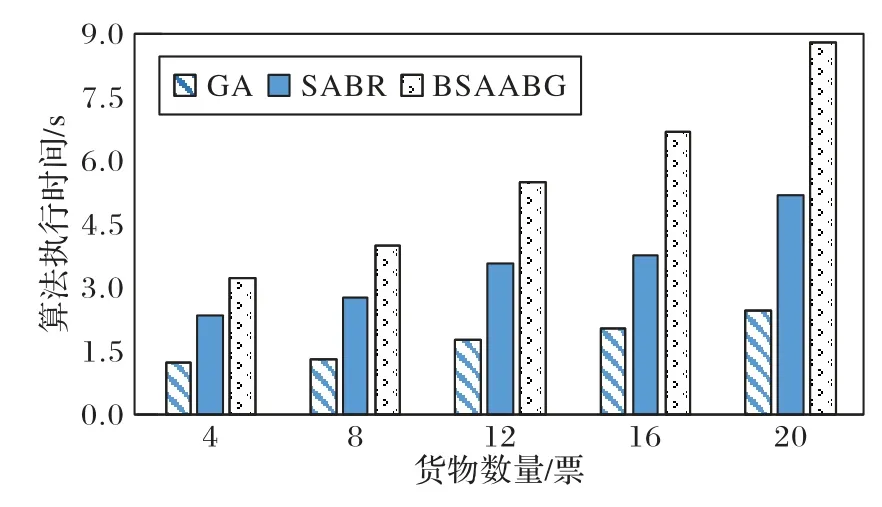
图7 货物数量对算法执行时间的影响Fig.7 Effect of cargo quantity on algorithm execution time

4 结语

为了提高散货港口堆场堆位分配的合理性，使各票货物的堆位匹配度得到满足，同时提高堆场使用效率，降低港口作业成本，使得堆场分配效益最大化，本文首先建立货物选择堆位的博弈模型来分析堆位分配的行为，然后采用基于博弈论的散货堆场堆位分配算法求解模型。在某内河港口的真实堆场环境上进行测试，本文算法在货物平均满足度和堆场分配效益方面与贪心算法和SABR 算法相比均有所提升。但本文研究仍存在不足，堆场分配效益的计算具有一定的局限性。在考虑堆位分配模型的求解目标时，虽然考虑了两个方面的因素，但最后通过线性组合的方式形成了单目标，并引入了相应的参数。今后将深入研究多目标问题，将多目标求解和博弈思想融入模型求解中，进一步提升堆位分配效率，并提出更加完善的堆场分配效益计算方法。