基于时间反演的到达时间定位

（1.重庆邮电大学通信与信息工程学院，重庆 400065；2.移动通信技术重庆市重点实验室（重庆邮电大学），重庆 400065）

0 引言

随着物联网时代的到来，在许多室内环境中，人们对位置服务的精度要求越来越高［1］，基于用户位置信息的相关技术得到了广泛的发展及应用。超宽带（Ultra-WideBand，UWB）技术可以不借助载波进行通信，其传输功率低、抗干扰性强［2］。由于其易穿透障碍物、良好的测距分辨率和时间分辨率等优点，因此在复杂的室内环境中实现高精度定位有着巨大的应用前景［3］。超宽带定位技术包括到达时间（Time Of Arrival，TOA）定位、到达角度（Angle Of Arrival，AOA）定位和到达时间差（Time Difference Of Arrival，TDOA）定位［4］等。

在超宽带TOA 定位系统中，通常是利用第一条直射路径的到达时间进行定位估计［5］，由于多径效应的影响，导致不能准确地估计第一条直射路径的TOA，进而影响定位精度。文献［6］提出了一种基于能量检测的最大能量选择算法，通过设定阈值确定最大能量块来估计TOA，但阈值的设定会受到多径的影响；文献［7］提出了通过卡尔曼滤波融合多个低复杂度能量检测器的动态到达时间，实现TOA 估计，减小了阈值设定的限制；文献［8］提出了基于UWB 的TOA/到达角度（AOA）的联合估计器，使用基于能量的阈值交叉初步估计TOA，然后利用初步估计的对数似然函数的局部二维最大化联合进行TOA 优化和AOA 估计，表现出良好的定位性能；文献［9］提出了一种基于能量检测的最大似然TOA 估计方法，该方法利用较长的积分窗口，克服了与接收机的实际硬件限制；文献［10］提出了一种基于匹配滤波的广义最大似然（Generalized Maximum Likelihood，GML）算法，将发射信号与接收信号进行互相关运算后，根据最大值估计TOA，但多径会使得估计产生误差；文献［11］提出了一种三步匹配滤波检测的算法，尽量减少多径问题，并且能够在计算效率和估计精度之间取得良好的折中。基于上述研究，在TOA 定位中，多径效应使得TOA估计不准确，影响室内定位精度。因此，如何有效克服多径效应并准确估计出第一条直射路径的TOA 成为一个重要的研究方向。

文献［12］对时间反演技术的传播特性展开了研究，其特性能有效克服多径效应对信号的影响。时间反演技术在时域上对收到的信号进行时间翻转，等同于频域上的相位共轭［13］。在复杂多径环境下，经时间反演处理后的信号重新发送后，会在目标点呈现时空聚焦性［14］。空时聚焦特性能在一定程度上减少多径的影响，是时间反演在多径复杂条件下最明显的特性［15］，使其在室内定位研究方面有着巨大潜力。基于此，本文设计了一种将时间反演技术与TOA 定位相结合的方案，利用时间反演算法对发射信号进行处理，其接收端信号呈现空时聚焦特性，可以在输出波形的最高峰精确估计TOA值，再通过加权最小二乘（Weighted Least Squares，WLS）算法对不同的估计分量赋予相应的权值进行定位估计，以提升系统的定位精度。

1 系统模型

1.1 超宽带信号的产生

UWB 窄脉冲时间分辨率高、抗多径性强，并且穿透力强的特性使得其可在室内使用。

产生UWB可以通过窄脉冲，对高斯脉冲函数进行调制。

一阶高斯脉冲如下：

其中：α2=4πσ2，σ2为方差，可见高斯脉冲不含直流分量。脉冲的直流分量才能使得天线能有效辐射，本文采用的是高斯二阶导函数，如下：

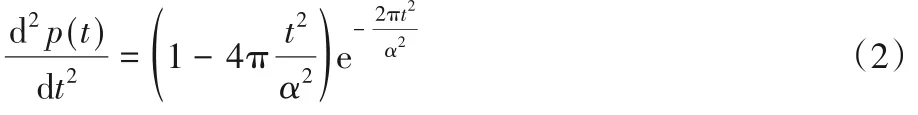
将一阶高斯脉冲导函数经过天线微分得到二阶导函数脉冲。根据文献［4］的描述，脉冲形成因子α决定脉冲宽度，α的范围是0.4～1 ns，本文α采用的是0.4 ns，其波形如图1所示。

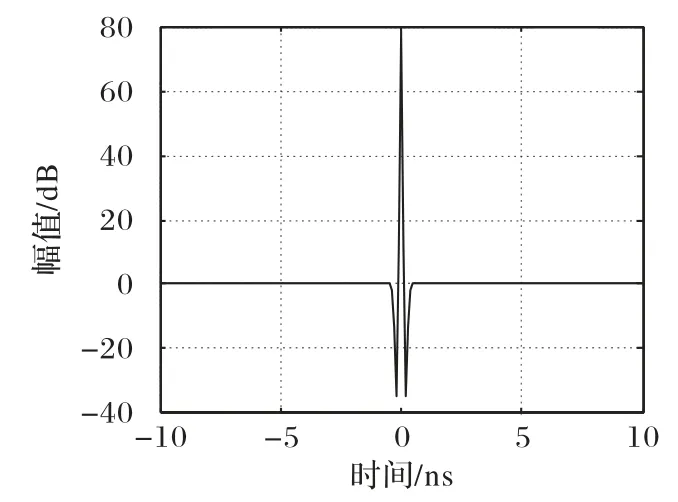
图1 高斯脉冲二阶导函数Fig.1 Gaussian pulse second-order derivative function

1.2 接收信号模型

对于实际的多径信道模型，其信道冲击响应的离散表达式h(t)可以表示为：

其中：αl和τl是第l条多径的幅度和时延。接收信号表示为：

其中：s(t)=(t-jTs)，p(t)是接收的UWB 脉冲，宽度为Tp；Ts是测距信号的持续时间；Es是测距信号的能量；n(t)是均值为0、谱密度为N0/2 的加性高斯白噪声（Additive Gaussian White Noise，AWGN）。

2 传统TOA定位

TOA 定位是根据目标点到参考点的距离来实现的，要想实现平面上的TOA 定位，至少需要设置3 个参考点，如图2所示。

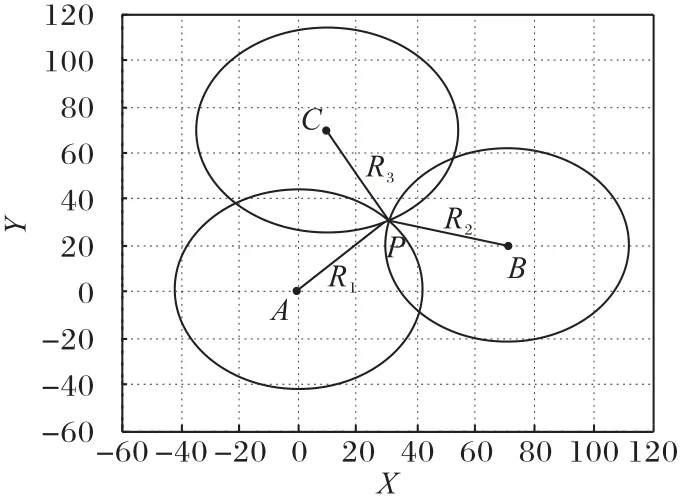
图2 TOA定位原理Fig.2 Principle of TOA positioning

TOA 定位需要分别得出参考点至目标点的到达时间即TOA 估计，再通过TOA 定位算法得出距离最终才能得出目标点位置，假设参考点至目标点距离为R，根据到达时间与光速c可得出距离，如式（5）：

2.1 TOA估计

传统的TOA 定位技术在参考点发射信号，目标点接收信号根据相干检测或非相干检测估计出TOA，即式（5）中的tTOA，如接收端使用GML 技术，即式（4）能表示成第一条路径、剩余路径与噪声的和，如式（6）所示：

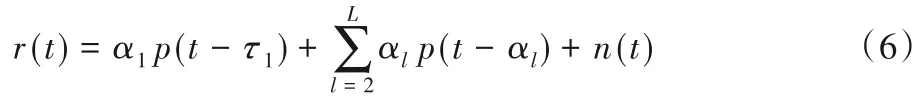
其中τ1＜τ2＜…＜τL。假设峰值时延τpeak和最大信道系数αpeak已知，则归一化信号可以定义为：

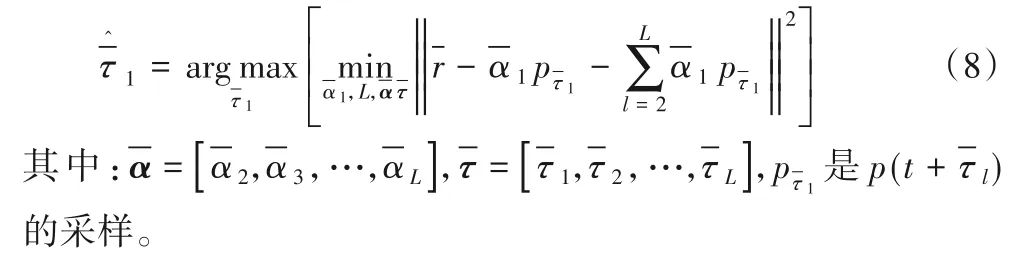
2.2 TOA定位

得到估计TOA 后，可以得到参考点到目标点的距离，如式（5），再根据毕达哥斯定理可得出目标点的位置，如式（9）：

其中如图2 中所示，(x1，y1)、(x2，y2)、(x3，y3)分别是参考点A、B和C的坐标，(x0，y0)是目标点P的坐标，R1、R2、R3分别是3 个参考点到目标点的距离。

假设R1＜R2＜R3，将式（9）两两相减得变为矩阵形式为：

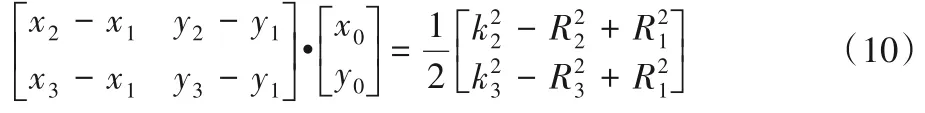
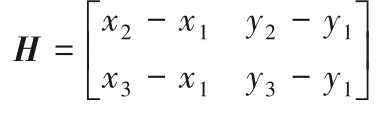
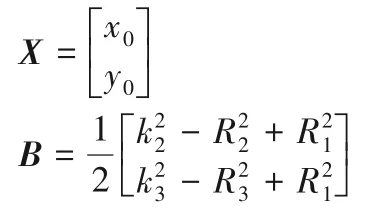
可以得出X=H-1B即目标点坐标。

3 基于时间反演的TOA定位技术

如图3 所示，接收端B 即目标点发送UWB 脉冲信号p(t)作为探测信号，发送端A即参考点对接收信号进行TR 操作并再送至B，根据接收端B 处接收信号的聚焦特性得出估计TOA 值。这就大大压缩了UWB信道的时延扩展，简化了接收机的结构。再采用加权最小二乘法定位算法进行定位估计，进一步提高定位精度。系统流程如图4所示。

图3 基于TR的TOA定位过程Fig.3 TR-based TOA positioning process

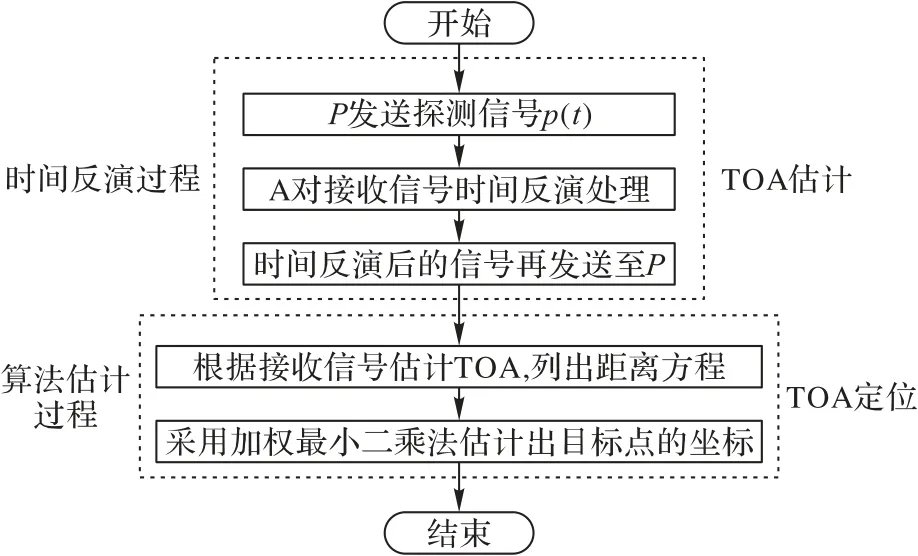
图4 系统流程Fig.4 System flow

3.1 TOA估计

时间反演是一种信号处理技术，TR技术通过探测信号估计信道脉冲响应（Channel Impulse Response，CIR），TR 技术成立的前提条件是多径环境、信道具有互异性以及时不变信道。TR主要分为探测阶段和反演阶段。假设发送端A想向接收端B发送消息，过程中为了完美估计CIR，假设噪声不存在，步骤如下：

1）探测阶段。

接收端B向发射端A发送探测信号p(t)，估计信道脉冲响应（CIR），如图5所示。

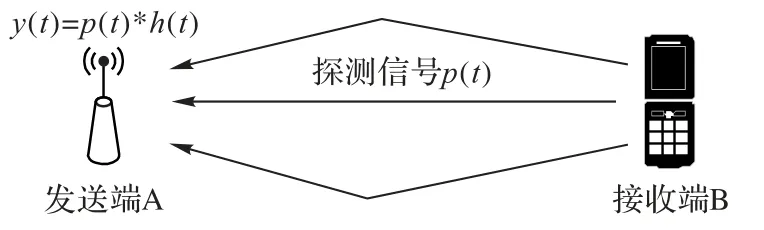
图5 TR探测阶段Fig.5 TR detection phase

探测信号p(t)经过超宽带信道后的输出为：

其中：y(t)表示探测信号经过超宽带信道后的输出；p(t)表示探测信号如式（2）；h(t)表示信道脉冲响应如式（3）。则根据式（11）可以估计出CIR。

2）反演阶段。

反演阶段如图6所示。

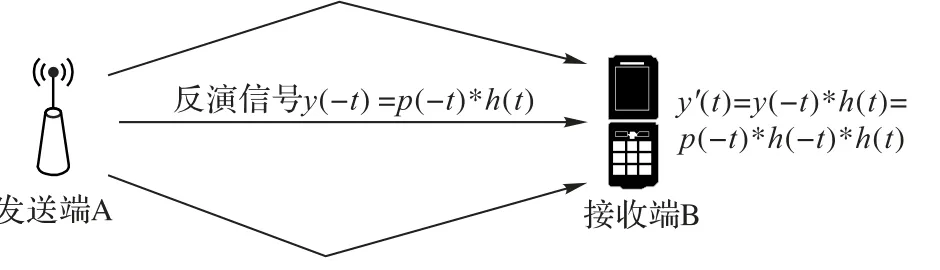
图6 TR反演阶段Fig.6 TR reversal phase

发送端A 收到探测信号脉冲后，对y(t)进行时间反演处理，得到信号如下：

其中，h(t)为信道脉冲响应。发送端A 将TR 信号经由原路径发送回接收端B，接收端B的接收信号表示为：

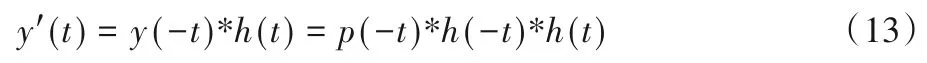
设H(t)为式（13）中的等效信道脉冲响应，可表示为：

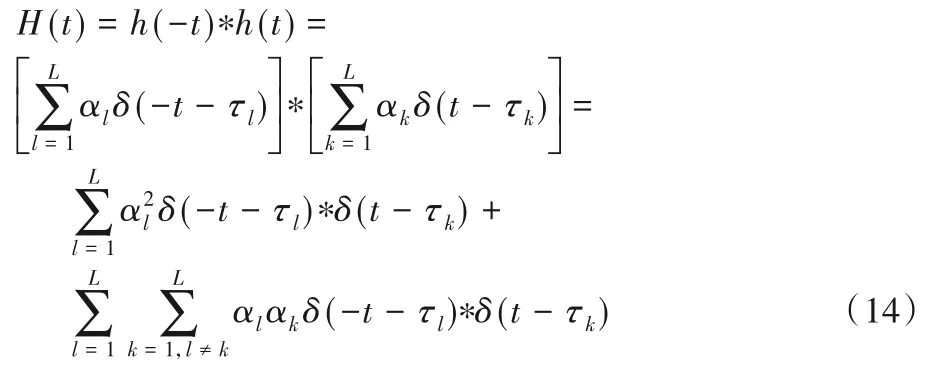
将式（16）中第一部分设为自相关R(t)和互相关Q(t)，可分别写成：

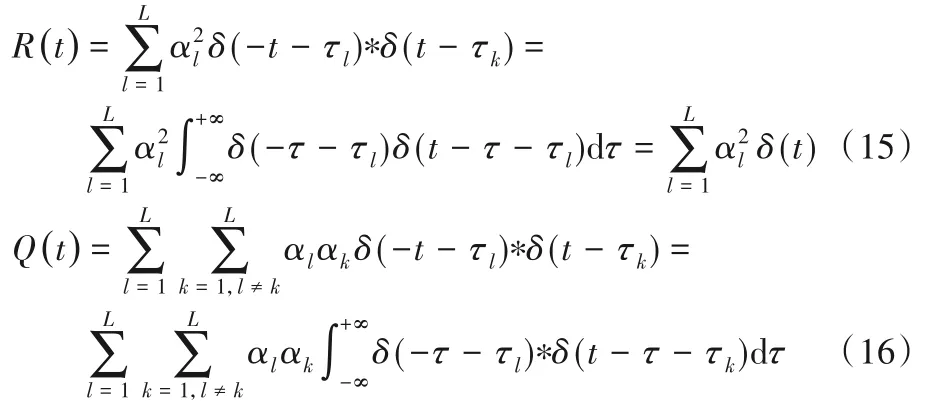
互相关函数Q(t)是各个不同传播路径的互相关函数，非相关多径信号卷积叠加后的结果是相互抵消的。而自相关R(t)时各个不同传播路径的函数，多径数越多，自相关函数越大，所以在多径环境中，Q(t)相比R(t)要小得多。根据式（13）可以看作探测信号经过信道脉冲响应H(t)，即一个h(t)的自相关输出。

那么时间反演后的接收端接收的信号波形会有一个明显的波峰即最高点如图7 所示，所以接收端接收信号输出波形的最高点所对应的时间指标即为估计的TOA。

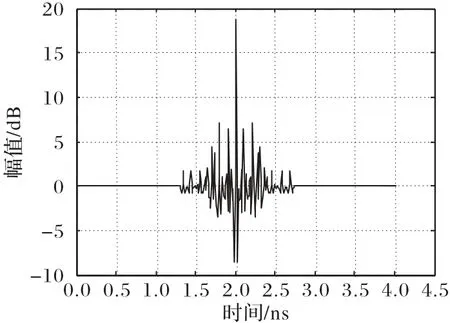
图7 TR聚焦特性Fig.7 TR focusing characteristic

3.2 TOA定位

得到估计的TOA 后，采用加权最小二乘法得出目标估计位置。首先假设在基于TOA 定位中，有N个位置已知的基站（参考点），每个基站的坐标为(xi，yi)，i=1，2，…，N，N表示基站（参考点）数量，未知标签（即目标点）坐标为(x，y)，则根据距离公式有：

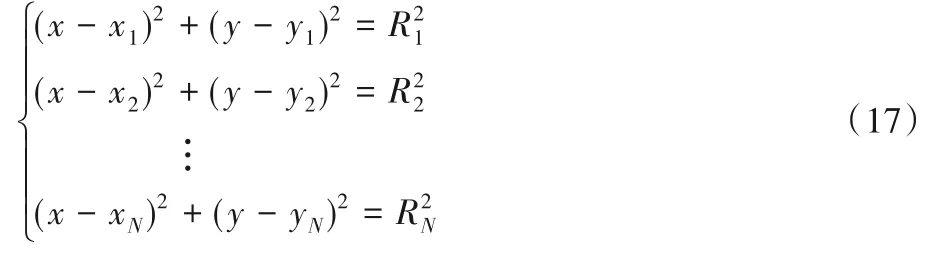
上述距离方程后需要进一步处理，即从第一式开始依次减去最后一式，得到一个矩阵表达式：

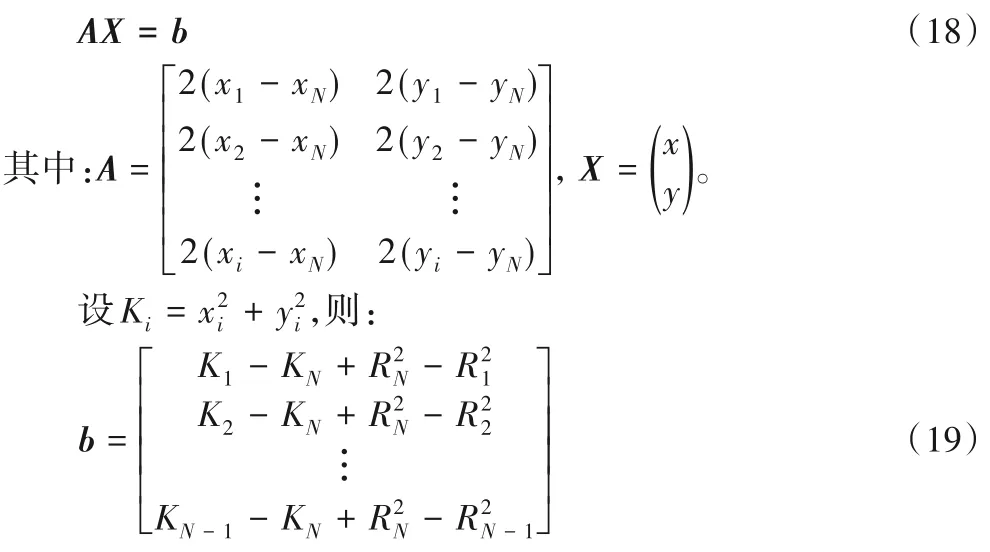
其中：Ki是中间变量，i=1，2，…，N，N表示基站（参考点）的数量。

由于存在误差，实际的线性模型为：

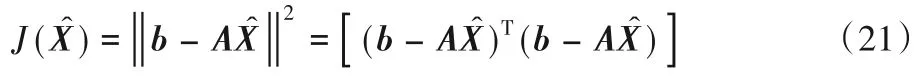
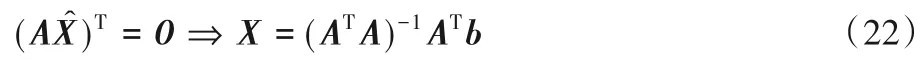
式（22）计算中的每一个分量权值相同，未考虑不同权值对计算结果的影响，本文采用WLS 算法在原有的最小二乘法（Least Square，LS）的基础上对不同分量加以不同的权值来计算估计值，则式（22）改为：

其中，W为已知的加权矩阵，测量精度高的数据权重大些，测量精度低的数据权重小些。本文采用的权值矩阵是根据测量误差矩阵V通过W=VVT得到的。利用已知的加权矩阵W，求出使式（23）最小的目标坐标矩阵X，得到目标的坐标。

4 仿真实验与结果分析

本章采用Matlab 工具对本文提出的算法进行仿真验证。TR过程中的探测信号采用二阶高斯脉冲导函数。

仿真中信道模型使用的是IEEE 802.15.4a CM-3，其典型环境是视距（Line Of Sight，LOS）条件下的办公环境。假设多径数为8，所有的噪声均为零均值高斯白噪声。参考点数目为3，坐标分别为（0，0），（70，20），（10，70），目标点坐标为（30，30）。

为了最大化信噪比，通过一个匹配滤波器使用探测信号p(t)的模板对接收信号进行处理。在不同的信噪比条件下，基于TR估计TOA偏移量与传统的GML估计TOA偏移量如图8所示。

仿真信噪比从2～32 dB，步长为2 dB。从图8 可以明显得出，采用TR技术估计TOA偏移量趋近于0，相比较GML而言，性能得到提升，在10 dB信噪比条件下，GML 估计TOA 有较大的误差，并且此条件下噪声对信号的影响很小，不会影响TR的性能。本文提出的利用TR估计TOA其性能得到验证。

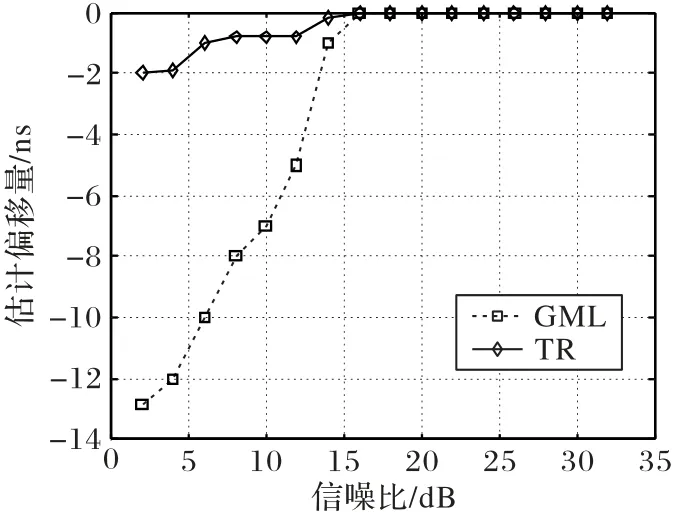
图8 TOA估计偏移量Fig.8 Offset of TOA estimation

图9 为信噪比为10 dB 条件下，基于GML 算法的TOA 定位，最后采用LS 估计目标位置。在10 dB 噪声条件下，由图9可得出，采用GML 估计TOA，三个圆相交偏差较大，TOA 定位精度不高。

图9 基于GML的TOA定位Fig.9 TOA positioning based on GML

图10是在信噪比为10 dB条件下，基于TR算法的TOA 定位，估计算法相同。考虑10 dB条件下噪声的影响，如图10所示，虽然由于噪声的存在，使得TOA 估计存在一定误差，3 个圆不能完美交于一点，但是相较于GML 算法估计TOA，TR 算法估计更为准确。

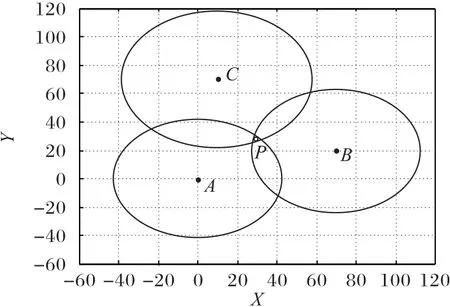
图10 基于TR的TOA定位Fig.10 TOA positioning based on TR

图11在LS估计算法下，分别比较TR 和GML估计TOA 的均方根误差（Root Mean Square Error，RMSE），其中TR 算法逼近克拉美罗界（Cramer-Rao Low Bound，CRLB），所以TR 算法估计TOA更加精确。

图12 是信噪比10 dB 条件下，四种算法的均方根误差比较，共测试10 次，得出每一次对应的RMSE。当采用GML 估计TOA 值，然后分别用LS 和WLS 进行定位估计时，使用WLS算法的均方根误差相对较小；当分别用GML 和TR 估计TOA值，采用LS进行定位估计时，用TR估计TOA 值的方法均方根误差更小；最后，GML 和LS以及TR 和WLS 两种方案相比，TR和WLS的均方根误差更小，性能更好。

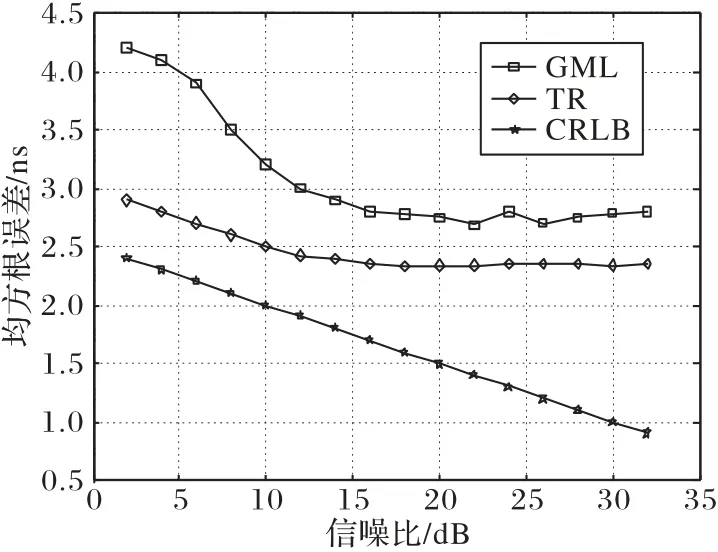
图11 GML和TR均方根误差比较Fig.11 Root mean square error comparison between GML and TR

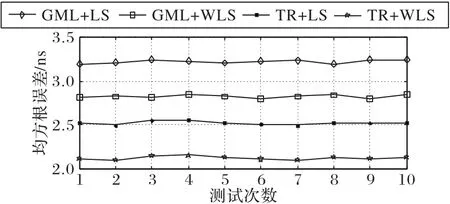
图12 GML和TR下的不同定位算法性能比较Fig.12 Performance comparison of different positioning algorithms under GML and TR

由图12 可以得出，在室内低信噪比条件下，本文提出基于TR 估计TOA，并以WLS 估计目标点的方案，相较于其他定位算法的RMSE显著减小，系统的定位精度有效提升。

5 结语

针对在室内多径环境下，传统超宽带TOA定位技术不能准确估计第一条直射路径的TOA的问题，本文提出了一种基于TR的TOA室内超宽带定位算法。首先，利用时间反演技术的空时聚焦特性减少多径的影响准确估计TOA；然后，采用加权最小二乘法进行定位估计。仿真实验验证了相较于传统的TOA定位技术，本文方案能有效地提升系统的定位精度。接下来的工作，一方面可以分析优化TR在探测阶段的信道估计；另一方面可以考虑在本文研究的基础上，降低信噪比，考虑严重噪声环境对TOA定位的影响，进一步实现复杂环境内的高精度定位。