基于改进粒子群优化和极限学习机的网络安全态势预测
(1.空军工程大学研究生院,西安 710051;2.空军工程大学防空反导学院,西安 710051)
0 引言
随着大数据时代的到来,网络给人们带来了极大的便利,但同时由于安全意识的缺乏,网络也带来了不可估量的安全问题。原始的网络安全预防主要通过防火墙、杀毒软件等技术被动防御外来的网络入侵,无法预测未来的走向。网络安全态势预测能够对网络状态进行分析,预测将来发生的状况,可在网络受到危险之前制定安全防范措施。因此,设计出有效、准确的网络安全态势预测模型是由被动防御转为主动防御的关键一步。
目前对网络安全态势预测模型的研究方法各种各样[1],传统的预测模型基本分为三种:统计分析模型、数据驱动模型和定性知识模型。统计分析模型如灰色预测需要建立精准的数学表达式,计算量大,且只能预测态势的大致趋势,不能预测精准的态势值;数据驱动模型如反向传播(Back Propagation,BP)神经网络需要利用大量的定量数据对模型进行优化训练,学习速度低,易出现过拟合、收敛慢等不足;定性知识模型只凭借专家经验及定性描述的数据无法有效利用定量信息,会出现组合爆炸及预测结果不准确等问题。文献[2]提出利用改进灰色关联理论对收集到的异常流量进行关联分析,实现校园网的态势感知,数据量运算大。文献[3]用BP 神经网络作为预测模型,通过人群搜索算法优化其参数,实现了更好的稳定性,但增加了训练时间成本。文献[4]采用模拟退火与高斯扰动的粒子群与支持向量机结合的预测模型,提高了预测精度,但收敛慢。文献[5]提出隐置信规则库模型,综合了专家经验和实验数据,成为复杂系统隐行为预测的一种有效方法。综合上述所提方法的优缺点,需要进一步寻求更优算法建立网络安全态势预测模型。极限学习机(Extreme Learning Machine,ELM)[6]是一种基于单隐含层前馈神经网络的最新研究成果,弥补了传统神经网络过拟合、收敛慢等缺陷。同时随着启发式算法的快速发展,众多学者对大量传统的启发式算法本身进行改进,进而优化神经网络,使其产生更好的训练效果。文献[7]提出一种改进遗传算法(Genetic Algorithm,GA),对遗传算法的种群、适应度函数、交叉概率及变异概率进行了改进,保持了种群的多样性的同时,避免了早熟收敛。文献[8]提出一种针对粒子群优化(Particle Swarm Optimization,PSO)算法收敛慢的改进,综合了指数衰减惯性权重和增强控制的学习因子,可以在较少的迭代次数获得更好的优化效果。文献[9]将粒子群算法与支持向量机结合进行网络安全态势预测,表明了该方法的可行性,实现对网络安全威胁的有效防御,但支持向量机本身并不能进行大规模样本训练。文献[10]将GA 与ELM 结合建立GA-ELM 预测模型,具有更高的预测精度和更好的泛化能力,但遗传算法的收敛始终较慢。文献[11]提出PSO 与ELM 组合算法,避免了ELM网络不稳定问题。
综上,基于ELM 的快速收敛能力及PSO 的稳定寻优性能,本文提出了一种改进粒子群优化极限学习机(Improved Particle Swarm Optimization Extreme Learning Machine,IPSOELM)算法的网络态势预测方法,通过改进PSO自适应调整全局和局部寻优能力优化ELM,使预测结果更加准确,并在保持快速收敛的同时,提高算法的稳定性。实验结果表明,所提方法比传统ELM、文献[10]中GA-ELM 算法和文献[11]中PSOELM 算法能获得更高精度的预测结果,同时建模效率也得到明显的提高。
1 极限学习机
极限学习机最早在2004 年被Huang 等[6]提出,通过随机选取输入层权重和隐含层偏置,以单隐层前馈神经网络为基础,依据Moore-Penrose 广义逆矩阵理论计算解析得出输出层权重,具有训练参数少、学习速度高、泛化能力强的优点。假设ELM 输入层、隐含层和输出层节点个数为分别n、l、m,其网络结构如图1所示。
对于给定的N个任意不同样本(xi,ti),其中xi=(xi1,xi2,…,xin)T,ti=(ti1,ti2,…,tim)T,则ELM的输出为:
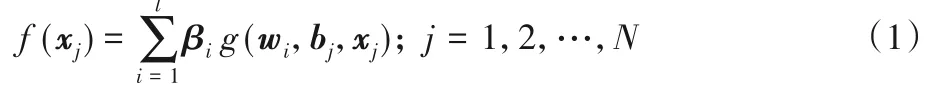
其中:wi=(wi1,wi2,…,win)T为输入层神经元与隐含层神经元之间的输入权值;βi=(βi1,βi2,…,βim)T为隐含层神经元与输出层神经元之间的输出权值;bi为隐含层神经元的偏置;g(⋅)为隐含层神经元的激活函数。ELM系统的矩阵表达式为:

其中:


其中:H为ELM 网络的隐含层输出矩阵;T为网络的样本期望输出矩阵。最终通过求解得到输出权值为:

其中H†为输出矩阵的Moore-Penrose广义逆矩阵。
由此得出,ELM在训练样本时无需借助梯度下降法,与传统的借助梯度下降法的反向传播神经网络相比,极大地减少了训练时间,同时保留了较为精确的预测能力。

图1 ELM网络结构Fig.1 Network structure of ELM
2 改进粒子群优化极限学习机
2.1 粒子群优化算法
粒子群优化算法最早是由Kennedy 等[12]于1995 年提出:在一个D维目标搜索空间中,存在某个包含a个粒子的群体,该群体中每个粒子都有一个初始速度vk、初始位置sk及适应值gk。在每一次迭代中,每个粒子不断更新着自己的位置和速度,同时通过适应值判断更新个体的最优位置pk和种群的最优位置pg。假设第一次迭代时最优位置即为粒子的初始位置,因此,种群中粒子的速度和位置的更新公式为:

其中:k代表粒子群中的第k个粒子;u代表目前的迭代步数;z称为惯性因子,其值为非负,当z较大时,全局寻优能力强,z较小时,全局寻优能力变弱。通过对z的大小进行调整可以控制粒子全局寻优和局部寻优的能力;c1、c2分别是粒子的个体学习因子和社会学习因子,其值为非负常数;r1、r2为在[0,1]范围内互相独立的随机数。
2.2 粒子群优化极限学习机模型
由于随机给定ELM 的输入权值矩阵和隐含层偏差,可能部分数值为0,使一些隐含层节点失效,从而导致预测效果不佳、稳定性不足等问题。为达到预测精度只有提高隐含层节点的数目,但隐含层节点数目的提高会出现训练样本适应能力差、泛化能力降低的问题。因此,为了保证ELM 在最优隐含层节点的条件下同时具有较高的预测精度,采用PSO 算法对其优化,借助PSO 的全局搜索能力将ELM 的输入权值和隐含层偏差进行最优搜索,既增强了ELM 的稳定性,又不会降低ELM 的收敛速度,在ELM 训练输入样本的过程中更加深入地学习样本之间的各种关系,其算法流程为:
步骤1 将样本数据分为训练样本和测试样本。
步骤2 通过样本数据确定ELM网络拓扑结构。
步骤3 初始化PSO 参数,种群的每个粒子代表连接权值和隐含层偏差,ELM 训练样本的均方根误差作为适应度函数。
步骤4 构建的训练样本输入ELM,根据ELM 得到的预测值评价每个粒子的适应度。
步骤5 令粒子k(k=1,2,…,a),当前的最优位置为pk=sk,对应的适应度为gbestk=gk;从粒子群中找出全局最优粒子,令其位置为pg,对应的适应度为gbest。
步骤6 对所有粒子执行如下操作:
1)按式(5)、(6)重新计算每个粒子的速度、位置,同时计算其适应度gk。
2)若gk>gbestk,则pk=sk,gbestk=gk;若gk>gbest,则pg=sk,gbest=gk。
步骤7 判断是否达到最大迭代次数,或适应度值是否达到给定的阈值,若否,转至步骤6;否则转至步骤8。
步骤8 将最终获得的权值和阈值作为ELM 的连接权值和偏差。
步骤9 将获得的最优权值和偏差应用到ELM 中预测得到结果。
2.3 IPSO-ELM的网络安全态势预测模型
虽然PSO-ELM 的预测能力有了较大提高,但PSO 在进行全局搜索时容易陷入局部最优点,这导致PSO-ELM算法稳定性较差。目前已有的方法包括对惯性权重的线性递减策略仍然不能权衡粒子的全局与局部搜索能力。为了解决这个问题,文献[13]中提出将目前迭代次数与最大迭代次数的比值作为惯性权重的变化,有效平衡了全局与局部的搜索能力,但不同的最大迭代次数之间相互比较发现,惯性权重变化量的突变使PSO-ELM算法的稳定性降低。同时,文献[14]研究指出惯性权重因子落在[0.3,0.7]为最佳区间,在此区间可更好地平衡算法的局部和全局搜索能力。因此,本文从PSO的惯性权重及学习因子入手,将静态参数改为可以随着迭代次数增加而自适应调整的动态参数,使z在迭代过程中更多地处于最佳位置,并且不同的最大迭代次数对惯性权重变化趋势的影响不大,同时提出了一种基于粒子个体随机扰动处理的策略,使陷入局部极值点的个体重新进行全局搜索。惯性权重调整公式如下:

其中h(umax)代表最大迭代次数的函数。如图2 所示,多个不同的最大迭代次数产生的惯性权重变化趋势相差不大,对算法的稳定性有所增强。
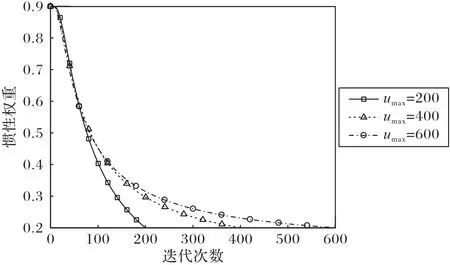
图2 惯性权重与迭代次数关系Fig.2 Relationship between inertia weight and iteration times
学习因子的调整方法为:算法在搜索前期,使c1值大于c2值,粒子主要进行全局搜索,避免陷入局部极值点;算法在搜索后期,使c1值小于c2值,粒子最终聚拢到全局最优区域。文献[15]指出c1的最佳取值范围为[2.5,0.5],c2的最佳取值范围为[0.5,2.5]。因此学习因子的调整公式为:

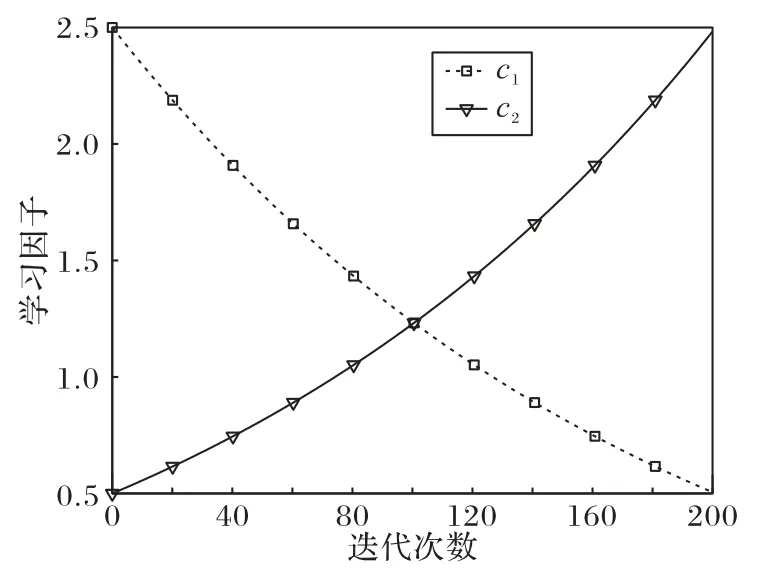
图3 学习因子与迭代次数关系Fig.3 Relationship between learning factor and iteration times
为解决种群粒子在搜索空间飞行寻找最优解时易陷入局部最优的问题提出粒子扰动处理策略,当判定粒子个体发生停滞状态时,通过停滞扰动处理,使个体粒子跳出局部最优,其判定处理公式为:

其中:ep为当前个体与局部最优个体之间的偏差;eop为当前个体与局部最优个体之间的阈值。
综上,经过改进的种群中粒子的速度和位置更新公式为:

最终,得到IPSO-ELM 的网络安全态势预测流程如图4所示。

图4 IPSO-ELM预测流程Fig.4 Flowchart of IPSO-ELM prediction
3 预测结果与分析
3.1 实验数据及其预处理
本文的实验数据来自文献[16]中搭建的网络环境所得出的网络安全态势值。该网络环境如图5 所示,首先模拟真实的黑客攻击行为,主要进行各种漏洞攻击;其次,通过对攻击的次数、种类进行统计,并判断主机遭受攻击后的受损程度建立网络安全评估系统来综合得出当前阶段的网络安全态势。实验中每隔30 min 进行一次统计并评估计算网络安全态势值,最终选取100 个态势值组成样本数据,并通过归一化处理排除误差偏大的可能,使网络安全态势值处于[0,1]区间,如图6所示。
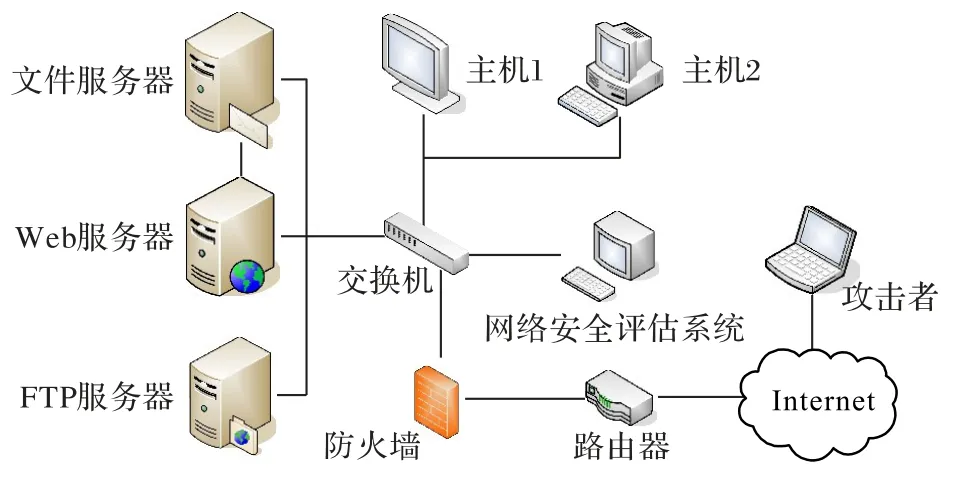
图5 网络实验环境Fig.5 Network experiment environment

图6 网络安全态势值Fig.6 Network security situation value
3.2 结果分析
实验过程中需要确定ELM 神经网络的各项参数,由于ELM 的输入层神经元个数代表样本数据的维数特征,而本文所对应的是某一段时间的网络安全态势值,所以采用滑动窗口法实现ELM 的输入数据。经过对网络安全态势的分析得出,一般网络当前的态势与之前3~5 个时间点存在着某种联系,因此将滑动窗口o的大小分别设置为3 和5 进行预测实验。隐含层神经元的个数对最终实验结果有一定影响,采用试错法确定隐含层神经元的个数,由于隐含层神经元个数通常不超过输入层神经元个数,所以隐含层神经元个数从1 开始依次增加到5,最终选取隐含层神经元个数为4。本文的目的是对未来的网络态势进行预测,因此输出层神经元个数为1,代表下一个时间段的网络安全态势值。
为了评价网络态势预测结果的优劣,选择平均相对误差(Mean Relative Error,MRE)、均方误差(Mean Square Error,MSE)、平均绝对误差(Mean Absolute Error,MAE)和拟合优度决定系数(the coefficient of determination,R2)作为预测结果的评价指标,其中MRE 的大小反映测量的可信度;MSE 的大小评价数据变化程度,其值越小,表明模型有更好的预测精度;MAE更好地反映预测值误差的实际情况。各评价公式为:
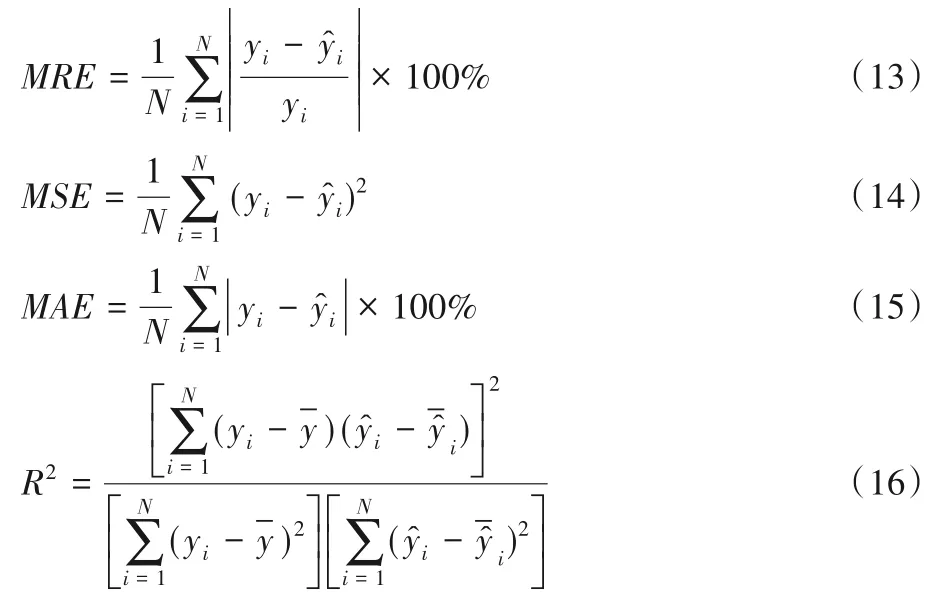
其中:yi为某一样本的实际值为某一样本的预测值;N为样本数为实际值的平均值为预测值平均值。
当滑动窗口的窗口值为3 时,采用前三个时间段的态势值预测下一个时间段的态势,其中部分样本已给出,见表1。经过IPSO-ELM 的预测,与传统的ELM、GA-ELM 及PSO-ELM对比,得出实验结果如图7 所示,各算法的收敛速度及评价指标对比如表2所示。
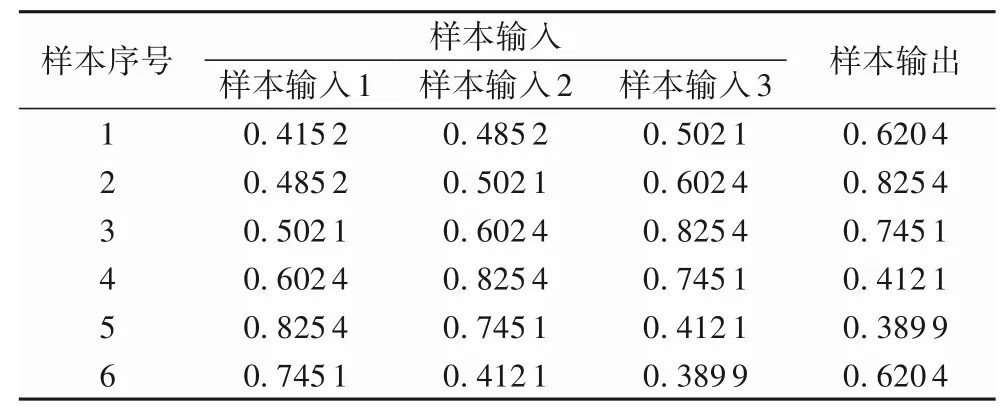
表1 部分样本输入输出(o=3)Tab.1 Inputs and outputs of some samples(o=3)
通过预测仿真得到如图7及表2对比结果。
当滑动窗口值为5 时,部分样本见表3,实验结果对比见图8,评价指标对比如表4所示。
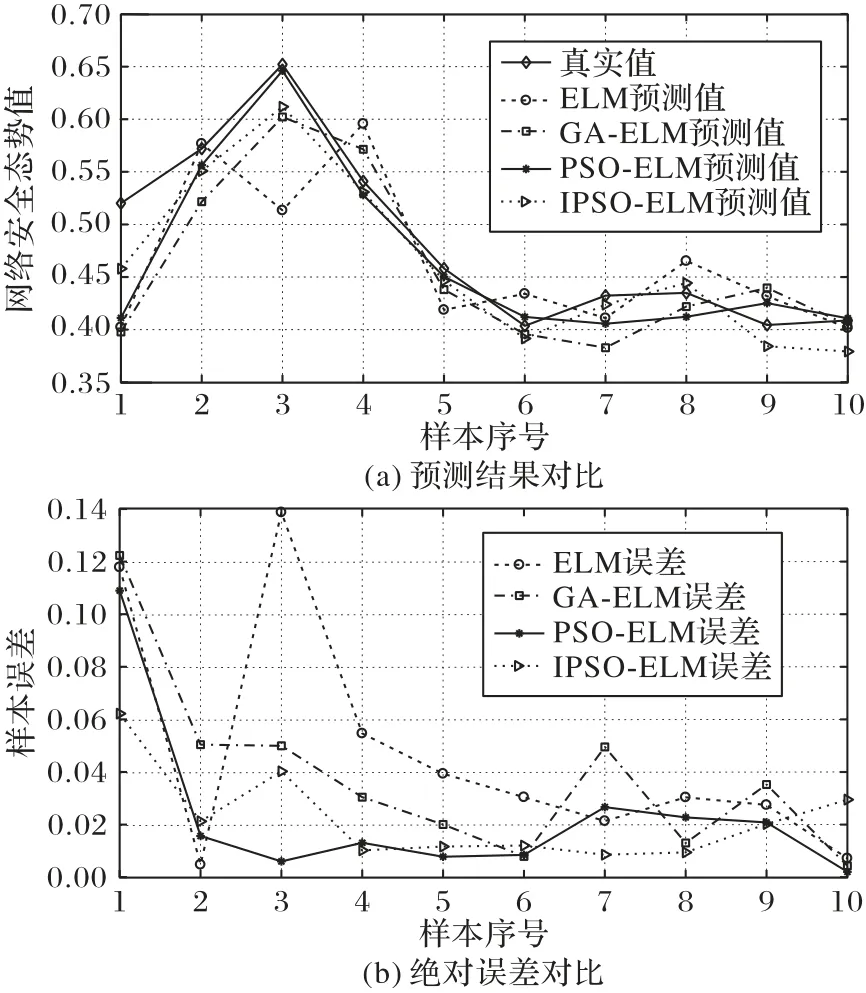
图7 窗口值为3时的实验结果Fig.7 Experimental results with window value of 3

表2 迭代次数和评价指标对比(o=3)Tab.2 Comparison of iteration times and evaluation indexes(o=3)

表3 部分样本输入输出(o=5)Tab.3 Inputs and outputs of some samples(o=5)

表4 迭代次数和评价指标对比(o=5)Tab.4 Comparison of iteration times and evaluation indexes(o=5)
通过实验结果对比分析可以看出,当滑动窗口值固定时,本文提出的IPSO-ELM 算法相较PSO-ELM 和GA-ELM 算法在网络安全态势训练数据的拟合度更高,对预测数据的准确性也有较大提高。虽然相较于ELM 收敛变慢,但当滑动窗口值为3 时,IPSO-ELM 比PSO-ELM 及GA-ELM 的收敛速度分别提高了29.2%和52.66%;当滑动窗口值为5 时,收敛速度分别提高了47.43%和66.94%。
对本文实验而言,当滑动窗口值不固定时,窗口值越大,训练输入数据时更能深度学习到数据之间存在的关系,从而对下一时间段的预测有一个更好的效果。

图8 窗口值为5时的实验结果Fig.8 Experimental results with window value of 5
4 结语
针对网络安全态势预测精度问题,本文提出了IPSO-ELM模型。ELM 神经网络可以快速地训练样本,加上IPSO 对其初始权值进行优化,可以精确地预测下一步的网络安全态势。经过实验对比表明,IPSO-ELM 模型在真实的网络环境中相较于GA-ELM 及PSO-ELM 有一定的优越性,收敛速度高,预测精度更高。但IPSO-ELM 也存在不足,在隐含层节点选取过程中偶然性较大,同时对于滑动窗口法窗口值的过大出现过拟合现象也未曾考虑,接下来将进一步研究自适应隐含层节点个数,从而更进一步提高收敛速度及预测精度。

