基于ZYNQ平台的YOLOv3压缩和加速

*

（1.西安交通大学电子与信息学部，西安 710049；2.西安交通大学人工智能学院，西安 710049）

0 引言

随着人工智能和云计算技术的快速发展，物体检测技术逐渐应用到人们生活的方方面面。例如，车辆检测在交通运输和安防［1］、自动驾驶［2］等领域有着广泛的应用。近年来卷积神经网络在物体检测领域取得了许多重大的进展，新的网络结构不断涌现，如R-CNN（Region-based Convolutional Neural Network）［3］、Faster-RCNN（Faster Region-based Convolutional Neural Network）［4］、SSD（Single Shot multibox Detection）［5］、YOLO（You Only Look Once）［6］等。这些新型的网络不断提升物体检测的精度，但它们的参数和计算量也在急剧升高。受制于计算、访存、功耗等诸多因素，通常很难将它们直接应用到车辆和无人机等移动嵌入式环境中。而将图像上传到云端进行检测则需要高速稳定的无线网络支持，系统的可用性直接受制于通信的质量［7］，而现有的网络环境很难支撑这一方案。因此，神经网络的参数量和计算量逐渐成为衡量算法性能的重要指标，它们决定了算法能否部署于端侧。

为了解决基于神经网络的物体检测技术在端设备实际应用中的计算负荷和性能问题，现有方法主要采用两类思路：一类是从网络设计开始，采用例如可分离卷积或者组卷积等技术来降低模型的参数，例如旷视的ShuffleNet［8］和Google 提出的MobileNet 系列［9-11］；另一类是通过对已有网络进行模型压缩，从而降低网络的参数与计算量。本文属于第二类，从模型压缩［12-25］和计算加速［26-33］两方面入手研究YOLOv3（You Only Look Once v3）［34］在端侧设备上的部署。Cheng 等［35］对这两者进行了综述，指出模型压缩的主要手段包括网络裁剪［12-17］、量化［18-22］和模型蒸馏［23-25］等。网络裁剪［12-17］通过分辨网络中各个部分参数的重要程度调整网络结构，剔除不重要的参数。网络量化［18-22］从数据表示层面对神经网络进行压缩。神经网络的参数通常只占用浮点数范围较小的一部分，因此使用浮点数表示神经网络参数存在很大的冗余。同时与整型运算相比，浮点数运算会消耗更多的硬件资源和计算时钟。网络蒸馏［23-25］在预训的教师模型基础上使用简单的学生模型来学习老师模型中的信息，从而减少模型的参数数量。

计算加速［26-33］方面主要结合硬件资源和神经网络的计算过程来进行模型加速：一方面根据计算的过程，可以适当地使用硬件特有的协处理器和单指令多数据流指令集来增加计算吞吐量［26］；另一方面可以结合现场可编程逻辑门阵列（Field Programmable Gate Array，FPGA）［27-29］和专用集成电路（Application Specific Integrated Circuit，ASIC）［30］等硬件资源结合计算过程的数据流设计相适应的计算模块，提升计算过程的数据吞吐量。

本文从神经网络压缩和加速两个方面同时入手对YOLOv3 网络［34］在端侧的部署进行研究，所提压缩方法可以推广到一般具有残差连接的神经网络。本文的主要工作有：1）提出了一种针对残差网络的模型压缩方法；2）设计实现了与ZYNQ 平台相适配的计算流程，实现了计算的加速。本文所提的压缩方法包括网络裁剪和量化两个方面，首先提出了一种针对残差网络的裁剪策略，将网络剪枝分为通道剪枝和残差链剪枝两个粒度，解决了通道剪枝无法裁剪残差连接的局限性。实验结果表明，该方法与通道剪枝相比能够进一步减少模型的参数和计算量。网络量化方面，本文引入并改进了一种基于相对熵KL散度（Kullback-Leibler Divergence）［36］的量化方法，能够在训练过程中统计模型的参数分布并在训练过程中计算量化造成的信息损失，从而优化量化区间减少精度损失。实验表明本文的压缩方法能够进一步降低模型量化过程造成的精度损失。

在计算加速方面，本文结合一种现有的FPGA 加速模块ZynqNet［29］设计并改进了针对Xilinx公司ZYNQ平台的8 bit卷积加速模块，通过使用8 bit 整型数据减少了片上存储和计算资源的消耗；然后，依据算法流程优化了片上缓存结构和流水线，进一步提升了硬件模块的计算性能；最后，结合Winograd［31］共享卷积计算的中间结果大量减少了计算资源的消耗。实验结果表明，本文的方案能够极大地提高了硬件计算卷积操作的性能，实现了比处理器（Central Processing Unit，CPU）和图形处理器（Graphics Processing Unit，GPU）等设备更高的平均能耗比，单位功耗下的计算能力更强。

1 相关工作

近年来卷积神经网络［1-6，34］在物体检测等领域取得了非常好的效果，解决了传统图像检测算法特征处理过程复杂、场景局限性强等问题，逐渐成为解决物体检测问题的主流方法。研究表明，一些神经网络通过极少的模型参数也能取得不错的检测精度，这表明深度神经网络普遍存在过量的参数和大量的冗余计算，随后研究人员开始关注神经网络的压缩和冗余计算的裁剪。另一方面，体系结构和硬件设备加工工艺的发展，也使得ASIC、FPGA 等平台的计算性能不断提升，如何结合硬件平台和神经网络计算过程也是一个重要的研究课题。接下来，将从三个方面简要综述本文涉及的技术和方法。

1.1 模型剪枝

在模型剪枝方面，Han 等［13］在2015 年首次提出将网络的连接性和权重分开训练，经过多次迭代后逐步裁剪模型尺寸。随后Li 等［14］在2016 年提出一种针对卷积核的神经网络剪枝方法，在每个卷积核中通过l1范数度量卷积核对网络贡献度，并根据贡献度对卷积核进行裁剪。针对裁剪过程信息损失大的问题，2017 年He 等［15］提出了一种基于Lasso 回归的通道稀疏化剪枝策略，通过回归和优化实现了与直接裁剪相比更低的信息损失。Liu 等［16-17］提出并改进了一种基于稀疏化训练和通道剪枝的模型裁剪方法，通过在训练过程中添加稀疏惩罚系数使得最终的模型信息在通道层面更加集中，最后根据批归一化层的γ参数裁剪通道，在训练时极大地减少了模型的信息损失和参数冗余。

1.2 模型量化

在模型量化方面，2015 年Han 等［18］提出一种基于共享权值的压缩方法，通过对训练好的模型的权重进行聚类，每个类别共享同一个数值，而后使用低比特数据索引权重，减少了参数体积。2016 年Courbariaux 等［19］提出一种参数仅由-1、1 构成的二值神经网络，直接训练不可微的量化模型，在简单的识别任务中取得了不错的结果。Rastegari 等［20］提出的XNORNet将特征和卷积的权重全部二值化，通过二值逻辑进行快速推理，也获得了类似的结果。文献［21］和文献［22］的工作均提出了一种基于整数的神经网络量化和训练方法。其中文献［21］在网络训练中通过浮点数模拟整数量化过程，实现了通用的量化模型训练方法，解决了量化模型不能直接训练的问题，在减少模型体积的同时充分利用了成本更低的整数运算。

1.3 计算加速

在卷积运算加速方面，Vasilache 等［30］在2014 年提出了一种通过离散傅里叶变换的卷积加速方法，通过快速傅里叶变换算法将特征图和权重转换为频域表示并利用乘法操作实现卷积，极大地减少了大卷积核计算的计算量。针对小卷积核计算的加速，Lavin等［31］提出一种基于Winograd变换的卷积计算加速方法，通过对特征图和权重以及输出做Winograd 变换将卷积转换为点乘操作，在增加少量加法运算的同时极大地减少了卷积运算的乘法运算，优化了计算的性能。Liu等［32］挖掘特征稀疏性，提出了稀疏Winograd 算法，进一步加速卷积的运算。Ioffe 等［33］提出了批归一化的折叠方法，在模型推理时将归一化操作与卷积层融合，减少推理过程不必要的计算。

2 改进的网络压缩策略

本章以YOLOv3 网络［34］为例对残差神经网络的压缩进行研究，并给出针对残差网络的压缩方法。YOLOv3 使用的特征提取网络是Darknet-53，它由五个串联的残差链［37］模块组成，在特征提取的基础上进行多尺度的网格划分，结合Anchor机制直接对目标的位置和类别进行回归预测。本文研究包括网络裁剪和量化两个部分。在裁剪方面，本文提出一种针对残差网路的裁剪策略，相较传统剪枝进一步减少了YOLOv3网络的计算量。在网络量化方面，本文提出了一种基于KL散度的模拟量化策略，能够在训练过程中统计参数的分布，并在训练过程中模拟量化造成的信息损失，从而减少量化过程的精度损失。

2.1 模型剪枝

首先对网络进行稀疏化训练，如式（1）所示，在每个卷积层反向传播过程中添加稀疏化惩罚项，使得训练过程中稀疏通道不断增多，稀疏化训练过程由参数λ控制：

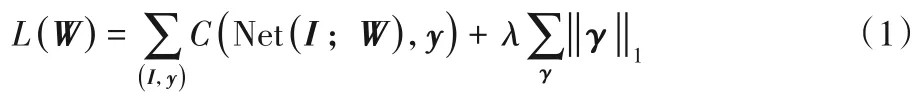
其中：Net 代表YOLOv3 神经网络；W是网络的参数；I是输入的图像；y是针对该图像的真实物体标签；C度量网络的输出和真实标签之间的损失；γ是神经网络中所有批归一化层的γ参数；‖ · ‖1对应l1范数。在稀疏化训练中，由于存在稀疏化惩罚项，训练过程将会产生大量的稀疏通道，稀疏通道的数值趋近于零，批归一化中的γ系数决定了该输出通道对后续计算的重要程度。通过分位数筛选掉γ较小的通道即可完成稀疏化通道剪枝。

如图1 所示，左侧为第i层卷积的输出通道，批归一化层经过稀疏化训练可以得到一组权重，其中权重相对较小的通道可以视为冗余通道。图中虚线代表对应的特征图通道将会被裁剪，卷积核中的对应通道以及对应批归一化参数可以直接从模型参数中移除。

其中：ic，oc分别是输入、输出通道的索引；F是高维特征图，W是卷积神经网络的参数，这里特指第i到第i+1层的卷积核；μic和分别是针对输入特征的批归一化处理的均值和方差；ε2是一个较小的数值，防止产生分母为0的情况；是批归一化的γ系数，⊗是卷积操作。

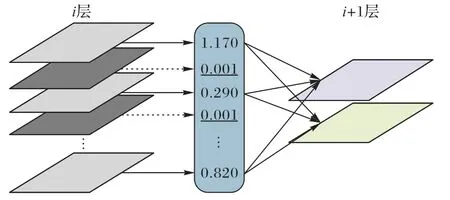
图1 稀疏化通道裁剪示意图Fig.1 Schematic diagram of sparse channel pruning

对于带有残差连接的神经网络，由于需要保证残差连接的结构，残差连接处的输入和输出通道需要保持一致，无法直接进行裁剪。Darknet-53中每个残差块由一个1× 1的卷积层和一个3× 3 的卷积层组成。如图2 所示，1× 1 和3× 3 卷积层之间可以直接进行裁剪，这是通道内的裁剪。如果直接对3× 3 的输出通道进行裁剪，可能会使得它与图2 右侧残差连接的通道数不一致，因此无法直接进行。

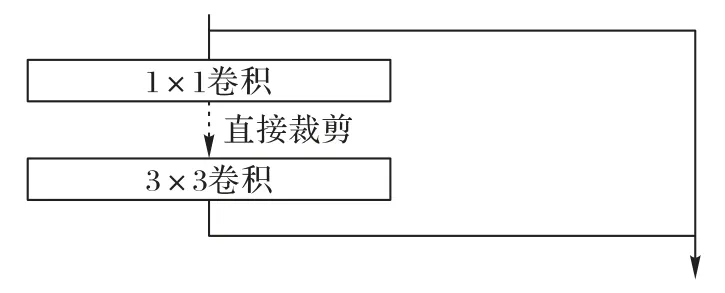
图2 残差连接中的通道剪枝Fig.2 Channel pruning in residual connection

虽然通道裁剪能够一定程度上减少网络的冗余参数，但残差连接中的通道仍然有许多冗余。通过本文提出的残差链剪枝，能够在通道剪枝的基础上进一步减少模型的参数量。在残差网络中，残差链可以看成是多个残差块输出的累加，因此残差链的输出通道的权重取决于每一接入残差块输出通道权重的叠加，对残差连接的剪枝需要对最终各个残差块输出的γ系数求和作为评估残差链通道权重的依据。如图3所示，本文的裁剪分为通道剪枝和残差剪枝两个粒度。

通道剪枝的对象为左侧1× 1 卷积的输出通道和3× 3 卷积的输入通道。残差链粒度包括右侧残差连接的输出通道和左侧3× 3 卷积的输出通道。残差剪枝需要协作各个残差块的输出通道，因此比通道剪枝更为困难。在实际裁剪过程中首先进行通道粒度的裁剪，而后在残差链粒度对每个残差链的通道数进行裁剪。在裁剪过程中，一次裁剪掉大量的通道通常会造成严重的精度损失。本文采用多次迭代进行稀疏化剪枝、剪枝后引入精调来保证精度。

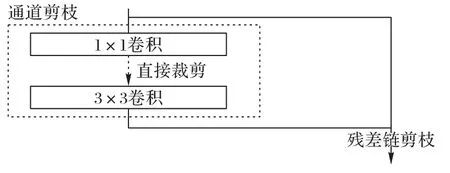
图3 通道剪枝与残差链接剪枝示意图Fig.3 Schematic diagram of channel pruning and residual connection pruning

2.2 模型量化

模型裁剪从结构上优化网络的冗余量，网络量化则从数据表示方面着手，文中将神经网络参数量化为8 比特的整型。通过神经网络参数分布可知，相对于浮点数的表示范围，卷积神经网络的输出通常局限在非常小的范围内，因此神经网络的数据表示中也存在冗余。通过将浮点数映射到低比特的整数，一方面能够使用低成本的整数计算单元，同时减少模型计算的访存总量。对称量化的计算过程如式（3）所示：

其中Δ为量化步长。对称量化中如果Δ是根据最大值以及量化位数确定的，会导致式（3）中Δ数值过大，使得更多的浮点数值落入同一个整数值，存在着较大的信息损失。

借助KL 散度可以选择出合适的Δ值使得最终的信息失真最小。KL散度的定义如下：

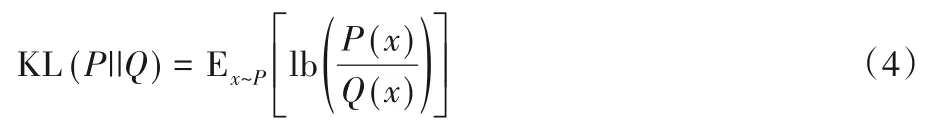
其中P和Q分别为量化前后参数的分布。

本文提出一种结合KL 散度［36］和模拟量化的模型量化策略，能够在模型训练过程结合KL 散度进行量化，在训练过程中将量化造成的信息损失考虑在内，减少精度损失。首先，在训练过程中统计网络每层参数的l1范数的最大值hmax和参数分布的直方图h，其中，直方图将区间[0，hmax]划分成2 048 等份并统计落在各区间参数的个数。如果在迭代过程中遇到更大的上限hmax，则重新统计直方图，迭代一定轮数并获得稳定的直方图作为P。

假设b是上述量化的中心点，量化需要确定一个区间[0，bj]其中j∈[129，2 048]，根据8比特量化的需要，将这个区间划分成128 个小区间（8 比特量化的区间为[-127，128]，为了简便认为负区间也量化为128 个等级，事实上仅有127 个等级）。

量化区间的选择带来了失真，如果j选择过大，存在量化步长过大带来KL 散度增大；但是如果j选择较小，存在丢失l1范数值较大的参数，也会带来KL 散度的增大。因此，j的选择应该是一个综合了步长和区间的最佳值。求解最优的j*使得量化后Q的分布与P分布的KL 散度最小，同时使得精度满足一定要求。计算出对应的量化区间的上限H128=(hmax×j*)/2 048，式（3）中的步长则可以由这个上限确定。

在训练过程中，分别对卷积权重的各个输出通道以及卷积层输出的激活值使用上述的模拟量化算法，在训练过程中统计数值分布并在浮点数上模拟量化造成的精度损失。由于使用了KL 散度量化，统计出的H128值通常小于统计值的最大范围，而且随着模型的训练，统计值的范围也在不断变化，因此对于超过界限的数值不能限定量化范围，否则会使模型无法收敛，训练过程中动态更新这个上界。

3 基于ZYNQ的加速模块

3.1 硬件平台环境

ZYNQ 平台是Xilinx 公司推出的低功耗嵌入式平台，包括PS（Processing System）和PL（Program Logic）两个部分。PS 部分主要由处理器构成，通过编写程序进行控制。PL 部分由可编程逻辑电路组成，通过编写硬件逻辑实现计算和控制。PS部分和PL 部分通过AXI（Advanced eXtensible Interface）总线进行交互，包括通常用作控制总线的低速总线AXI-GP和用作高速数据传输的AXI-HP 总线。AXI-GP 总线通常由PS 端作为主设备控制外设运行，AXI-HP 总线由PL 端作为主设备，可以直接访问动态随机存取存储器（Dynamic Random Access Memory，DRAM）和一致性缓存，在大量数据通过一致性缓存时会极大降低PS端的运行速度。

本文设计的系统结构如图4所示，右上角为ZYNQ处理平台，与DDR2（Double Data Rate 2）和处理器相连接；中间部分上面是AXI-HP 高速总线的交叉开关矩阵（Crossbar），负责处理加速模块的内存数据请求；下面是系统的时钟和复位信号控制模块，负责PL 端的时钟分发和复位，系统PL 端的工作频率是200 MHz；左侧上边是FPGA 加速模块，主要使用ZYNQ平台的DSP48E 和Block RAM 实现计算加速和片上缓存。由低速总线负责卷积参数的输入和运行状态的控制。下面是低速总线的Crossbar，负责下发PS端的控制指令和参数。

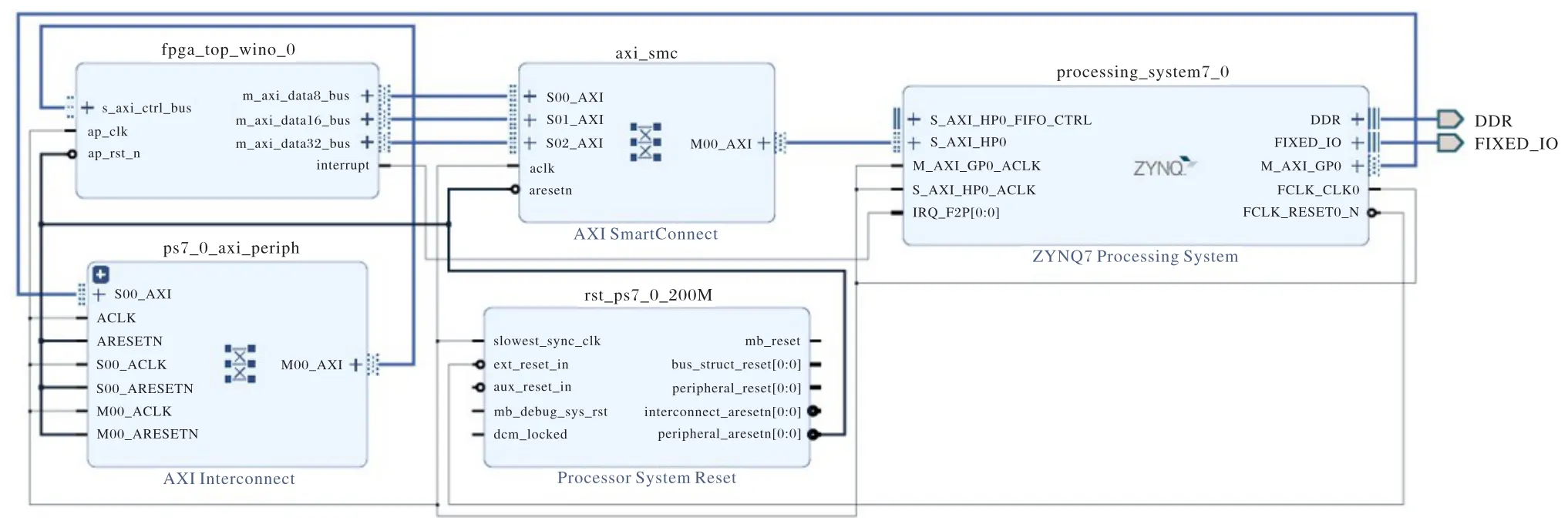
图4 系统结构Fig.4 System architecture

3.2 计算模块设计

计算模块的设计是在ZynqNet［29］的基础上修改的，ZynqNet 是在ZC7x045 平台上实现的基于GoogleNet［38］的手写数字识别的浮点计算加速模块。本文在ZynqNet［29］的基础上删除与YOLOv3［34］计算无关的全局池化（Global Pooling）、存储控制（Memory Controller）等模块、使用8 bit整数作为推理的数据类型并使用AXI-Burst来提高硬件在读写DRAM 时的性能。在ZC7x020 平台上重新设计并优化了卷积计算模块，优化策略主要参考文献［39］。

如图5 所示，本文的设计模块包括配置面板（Configure Board）、输入缓存（Inputs Cache）、权重缓存（Weights Cache）、输出缓存（Outputs Buffer）、处理单元（Processing Element）和后处理（Post-process）等几个模块，下面分别对各个模块的划分进行介绍。

配置面板：模块存储卷积计算的各个参数，包括输入特征图的长宽、输入输出通道数、卷积核大小、卷积核移动步长、是否使用Leaky RELU［40］激活函数。

输入缓存：由16 个块状随机存取存储器（Block Random Access Memory，Block RAM）并联实现，按照高度、宽度、通道的顺序存储输入特征图。16 个Block RAM 中每4 个存储输入特征图的一行，按照输入特征图的行编号余4 选择Block RAM。16个Block RAM 可以同时存储输入特征图的4行。在列上面也是按照特征图的列编号余4 选取存储器。在读取特征图时允许最多对4 × 4 个端口同时读取数据。在一个时钟周期内即可读取计算所需的特征图，减少了特征图读取的延迟。

权重缓存：由N_PE×3×3 个Block RAM 并联实现，按照输入通道、输出通道、卷积核高度、卷积核宽度的维度次序存储特征图，用以缓存处理单元所需要的权重系数。输出通道按照余N_PE的次序依次映射到各组Block RAM 上。每个处理单元和9 个Block RAM 相关联，从而允许计算单元在一个周期内读取所需的权重数据。

输出缓存：由N_PE个Block RAM 构成，保证每个处理单元计算之前能够读取输出通道的数值并在计算后将累加的结果写回存储中。

处理单元：由9 个数字信号处理器（Digital Signal Processor，DSP）组成，负责对输入的特征图和权重进行乘加操作，并将最终结果累加到输出缓存中。由于本文平台资源的限制，这里选定N_PE=16。

后处理：模块负责在写回输出特征图通道数据之前对输出进行批归一化、激活和重量化操作。在完成后将结果写回内存。

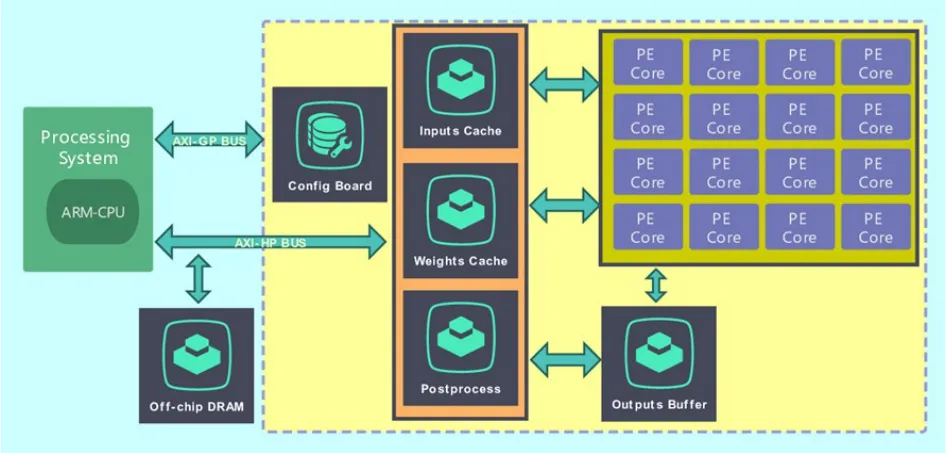
图5 加速模块结构Fig.5 Acceleration module architecture

3.3 算法流程

本文模块结构根据YOLOv3 卷积层的计算过程实现，算法1 描述了卷积模块的计算过程。从中可知，特征图的存储形式是F[ih，iw，ic]，其中ih、iw和ic分别是对特征图像高度、宽度和通道数的索引；权重的存储形式是W[ic，oc，fh，fw]，其中ic、oc、fh和fw分别是对卷积核输入通道、输出通道、高度和宽度方向进行索引。这里重新调整了输入通道的位置改变了加载数据的顺序，同时增强了数据访问的局部性，在计算过程中充分利用模块的I/O端口。

算法1 朴素卷积算法。

经过优化，本文实现比从ZynqNet 移植的基准实现有了明显的性能提升。在验证算法计算结果正确后，本文结合Winograd算法对模块结构进行调整，进一步增强硬件性能。

如算法2 所示，矩阵G、B和A分别是权重、输入和点积结果的基变换矩阵［31］。借助Winograd 变换F（2，3）能够在增加一些加法运算的同时将乘法操作从9 个减少到4 个。针对现有的设计结构，本文调整了权重缓存R的形状，使用16 ×N_PE个Block RAM 存储GRGT变换后的权重。在读取输入S后进行BTSB变换，由于硬件资源的限制，将N_PE从16 减小到8，在点乘输出T后进行ATTA变换，能够在增加少量加法计算资源同时的节省3/4的输出缓存大小。

算法2 Winograd F（2，3）卷积算法。

4 实验与结果分析

本文用KITTI（Karlsruhe Institute of Technology and Toyota Technological Institute at Chicago）［41］数据集中的车辆和行人两类数据对上述的压缩算法进行了实验验证。训练数据集中包含了3 700 张大小相近图片，测试数据集中包含了3 800 张图片，主要包括行车和道路场景下的车辆、行人等物体的标注信息。图6 中是数据集中的样例图片。在训练之前首先要按照PASCAL VOC（Pattern Analysis，Statistical modelling，And Computational Learning Visual Object Classes challenge）的标注格式对数据集的标注进行转换。

1）模型裁剪结果对比。

模型剪枝实验首先进行稀疏化训练，训练使用1E-4的学习率和1E-5的稀疏化惩罚系数，再分别进行通道剪枝和残差链剪枝，最后进行精调。表1 中对不同的裁剪方法进行了对比，由表1 可知，模型裁剪能够极大地减少模型的计算量，而本文提出的方法能够进一步地减少模型计算量。这里使用平均精度（Average Precision，AP）度量模型性能。由表1 可知，与直接通道剪枝相比，本文的方法能够在略微降低精度的情况下进一步减小模型的尺寸和计算量。

图6 KITTI数据集示例数据Fig.6 KITTI dataset sample

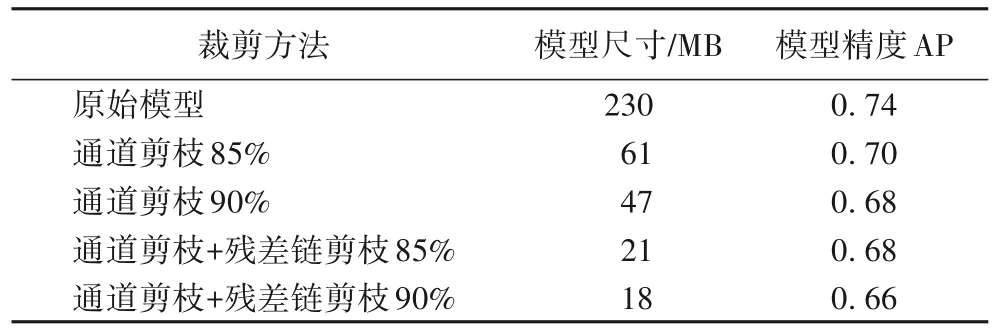
表1 模型裁剪结果对比Tab.1 Comparison of model pruning results

图7 给出一些通道剪枝+残差链剪枝85%模型对应的检测结果图，由图7 可见，裁剪后的模型能够较为准确地预测出车辆的大小和位置。

图7 裁剪后模型的检测结果Fig.7 Detection results of pruned model

2）模型量化结果对比。

模型量化在Darknet-53 上分别实现了不同的量化方法，并以表1中通道剪枝+残差链剪枝85%为基准进行验证，实验结果如表2所示。

表2 模型量化结果对比Tab.2 Comparison of model quantization results

由表2 可以看出，由于存在离群值，使得最大最小值量化过程存在较大的信息损失，精度降低严重。结合KL散度量化能够一定程度上减少信息损失，再结合模拟量化对模型进行微调，能够有效地减少模型的精度损失。其中，由于使用了批归一化，激活值的分布关于零点基本对称，因此使用对称量化前后的精度损失较小。最后，本文尝试了使用每通道量化的方式，对每个卷积输出通道分别进行量化，增加了模型参数数量，但可以进一步减少精度损失。

在表3 中，将本文所提的压缩算法与经典的YOLOv3 tiny进行对比，这是YOLOv3 提供的一个压缩版本，实验使用基本操作数（Basic OPerationS，BOPS）比较卷积操作的计算量，其单位为109（Billion）。本文所提压缩方法获得的模型与YOLOv3 tiny 的BOPS 接近，但获得了超过YOLOv3 tiny 的7 个百分点的性能，同时模型尺寸约为YOLOv3 tiny 的六分之一。此外，相较于其他裁剪与量化方法，本文所提方法在保持高性能的前提下也具有较高的压缩比，实验验证了本文所提压缩方法的有效性。

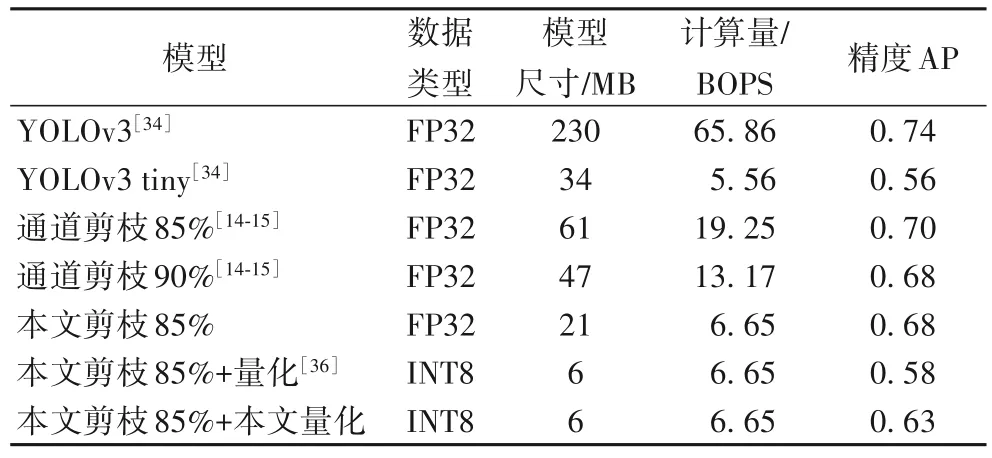
表3 不同压缩算法的模型尺寸、计算量与精度对比Tab.3 Comparison of model size，computational cost and accuracy for different compression algorithms

3）加速模块性能对比。

对本文涉及的几个加速模块的实现进行比较，包括ARM（Advanced RISC Machine）处理器版本的实现、从ZynqNet 移植的基准实现、本文设计和优化的没有集成Winograd 算法的实现和集成Winograd算法的实现，结果如表4所示。

由表4 可见，在端设备上直接使用ARM 处理器进行推理是不现实的，借助FPGA 进行8比特推理能够有效提升计算速度，在ZynqNet 的基准实现上，本文的设计和优化能够提升模块的平均性能，有力地支持神经网络的端侧推理。表4 中，平均性能通过迭代200 轮进行统计，性能的度量单位是每秒十亿计算数（Giga Operations Per Second，GOPS）。

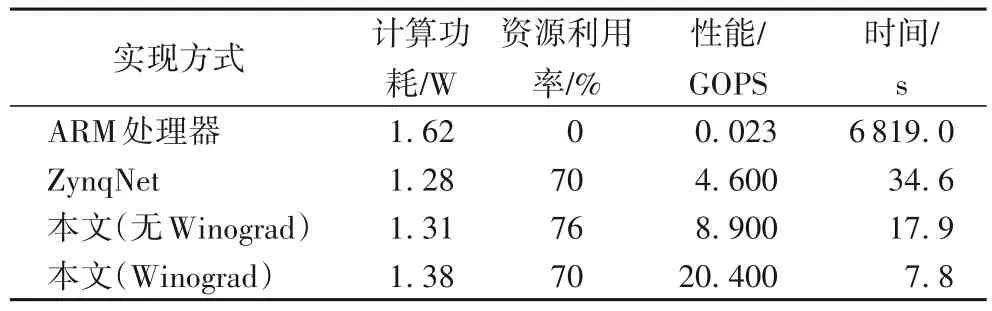
表4 不同计算加速模块的功耗、资源利用率与性能对比Tab.4 Comparison of power consumption，resource utilization rate and performance for different computation acceleration modules

接下来，本文结合现有的包括CPU、GPU、FPGA 等多个平台的实现结果［42-43］对本文在ZYNQ 平台上的计算加速算法进行评估，结果如表5 所示，通过单位功耗实现的操作总数评估各实现的能耗比。本文实现的非Winograd 加速模块的平均性能与GPU 样本相近，比FPGA 样本略高。具有Winograd 的加速方案能够在无Winograd 加速的基础上提升一倍多的能耗比；与其他平台相比，本文集成了Winograd 的方案能够在更低的功耗下取得较高的计算性能。

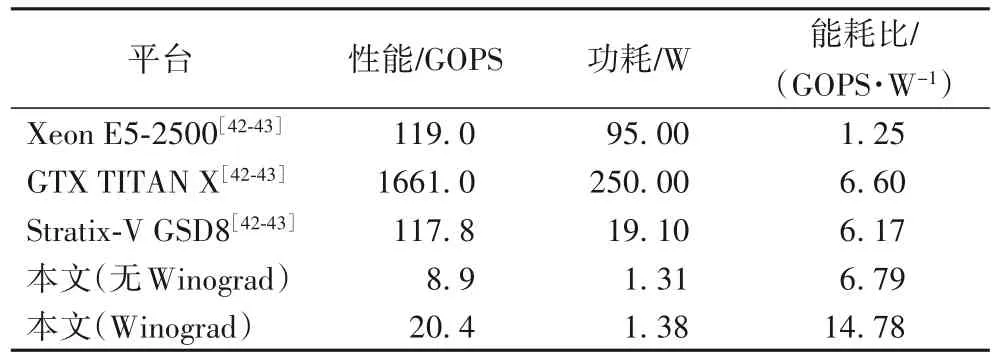
表5 不同平台的性能、功耗以及能耗比对比Tab.5 Comparison of performance，energy consumption and energy consumption ratio on various platforms

5 结语

本文围绕YOLOv3 网络在低功耗场景下的应用进行研究，通过模型压缩与适配端侧设备的计算加速实现了网络在ZYNQ 平台的部署，达到了较高的能耗比。一方面，本文设计了针对残差网络的裁剪方法，通过引入针对残差链的剪枝和按通道的量化实现了以较低的精度损失获得较高压缩比的目的。另一方面，本文在ZynqNet 的基础上设计实现了卷积加速模块，优化了片上缓存，集成了Winograd 算法，极大地提高了低功耗场景下ZYNQ 平台的卷积性能。与不同平台的比较表明，本文研究获得了较高的能耗比，能够加速推进YOLOv3以及其他残差网络在ZYNQ端侧的部署。

关于神经网络的压缩与部署，仍有很多值得探索的地方。例如，将本文所提压缩方案推广到具有池化等模块的网络，探讨适用更复杂结构的网络压缩方案是未来一个有价值的研究方向。另外，在加速模块部分，结合Chisel（Constructing hardware in a scala embedded language）等敏捷硬件开发工具，实现更细粒度的硬件结构控制，从而提高硬件资源的利用率、降低平均功耗也是值得考虑的一个研究点。