基于可行点追踪-连续凸逼近的MIMO雷达相容性波形设计
宋青青,许 菁,陈 伟,王鑫海
(中国船舶集团有限公司第八研究院,南京 211153)
0 引 言
随着雷达系统、通信系统等电磁辐射系统的发展,解决雷达与其威力范围内的己方电磁设备之间的相容性问题正在成为当前热点。根据雷达的阵元布置形式不同,多输入多输出(Multiple Input and Multiple Output,MIMO)雷达通常可分为分布式和共址两类[1]:分布式MIMO雷达的阵元间距较大,因此具有较高的空间分集增益[2];共址MIMO雷达收发阵元分布相距较近,能够提供高分辨率空间谱估计能力[3]。与相控阵雷达发射相干信号不同,MIMO雷达的各阵元发射信号相互正交。优化MIMO雷达波形达到干扰抑制的目的是当前的雷达研究热点之一。为了应对实际战场需求,MIMO雷达波形不仅要具有抗干扰能力,还需要满足当前的工程应用要求,包括谱相容性、低峰均比(Peak-to-Average Power Ratio,PAPR)、宽带和良好的自相关特性等[4-5]。
近年来国内外学者发表了诸多关于共址MIMO雷达波形设计的研究成果:在有限能量约束下,文献[6]提出了基于拉格朗日乘子法的波形设计方法;文献[7]针对多信号依赖干扰存在的情况下,以最大化最差信干噪比为准则,使用迭代算法实现了MIMO空时信号编码与空时滤波器的联合设计;为实现MIMO雷达的相容性波形与滤波器联合优化,文献[8]借助对偶上升法(Dual Ascent Method,DAM)[9],通过最小化雷达在其他己方电磁设备所工作的空频区域内的谱能量,实现对相容性波形的优化,相容性波形设计问题可看作一类非信号依赖性干扰抑制问题;文献[10]使用最优化方法的思想是最大化信干噪比,并给出了波形在低峰值平均功率比和有限能量约束下的闭式解;文献[11]提出单调误差约束改进技术(Monotonically Error-bound Improving Technique,MERIT)解决恒模二次优化问题(Unimodular Quadratic Program,UQP),而且给出了全局最优解与局部最优解;文献[12]将原UQP转换为二次优化二次约束规划(Quadratically Constrained Quadratic Programming,QCQP),提出用连续QCQP提炼(Successive QCQP Refinement,SQR)方法解决MIMO雷达波形设计问题;文献[13]针对连续相位优化与离散相位优化两种情况提出一种高效的迭代恒模波形求解算法;文献[14]将文献[13]中的算法思想与丁克儿尔巴赫(Dinkelbach)算法相结合,求解了二次分式的优化问题;基于随机化半正定放松技术,文献[15]提出了两种序列优化算法(Sequence Optimisation Algorithm,SOA),但该方法计算复杂度较大。目前雷达波形设计常见指标包括信号能量有限性、相似性、信干噪比需求和相容性,但同时考虑这4方面因素的成果较少。
为了减弱MIMO雷达与己方电磁辐射设备之间的相互干扰,本文以最小化己方电磁辐射设备所占据空频域范围内的雷达谱能量为准则,提出了基于可行点追踪-连续凸逼近(Feasible Point Pursuit-Successive Convex Approximation,FPP-SCA)[16]的雷达波形与空域-快时间域滤波器联合优化方法。相对于已有算法,本文算法不仅提高了波形相容性,而且实现了对信号依赖性干扰的有效抑制。
1 信号模型
假设雷达模型架构共址MIMO,接收阵列与发射阵列均为线阵,且分别有Nt与Nr个阵元,阵元间距为所发射射频信号的半波长。当指向角为θ时,发射导引矢量与接收导引矢量分别为
at=[1,ejπsinθ,…,ejπ(Nt-1)sinθ]T
ar=[1,ejπsinθ,…,ejπ(Nr-1)sinθ]T
(1)
令sp∈L为第p个发射天线的发射信号矢量,其中sp(l),l=1,2,…,L为sp的第l个分量,则空时发射矩阵可以定义为S=[s1,…,sNt]∈L×Nt,其向量化形式表示为s=vec(S)。设在雷达威力范围内存在K个目标和J个信号依赖性干扰。第k个目标所在距离门为mk,其方位角为θk,且ζk为第k个目标的反射系数,则相应的目标反射回波为
(2)
其中,Dmk∈L′×L表示为
Dmk=[0L×mk,IL,0L×(L′+L-mk)]T
(3)
式中,L′为每个天线在一个脉冲上的采样点数。
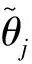
(4)

因此,总的接收信号可表示为
(5)
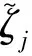
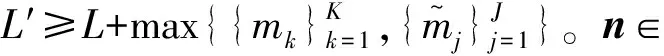
2 构建优化问题
优化雷达波形与滤波器的目的是为了解决共址MIMO雷达的相容性问题,并抑制信号依赖性干扰。为了确保所构建的数学优化问题符合实际情况,结合雷达实际需求,对雷达波形进行约束,具体包括相似性约束和信干噪比约束。约束条件的具体概念及数学表达式如下:
(1)相似性
为了保证最优波形具有已知波形的某些性质,如带宽、相关特性等,对所优化波形与参考波形之间进行相似性约束,相应的数学表达式为
‖s-s0‖2≤ε
(6)
其中,s0为一已知的参考波形;ε为相似性系数,用来控制优化波形与参考波形之间的相似程度,ε越小,所优化波形与参考波形相似程度越高。
(2)输出信干噪比
针对某个目标,信噪比定义为回波中该目标所反射的信号能量与信号依赖性干扰、噪声和其他目标的能量和的比值,也就是将除该目标外的其他目标也看作为干扰,表达式为
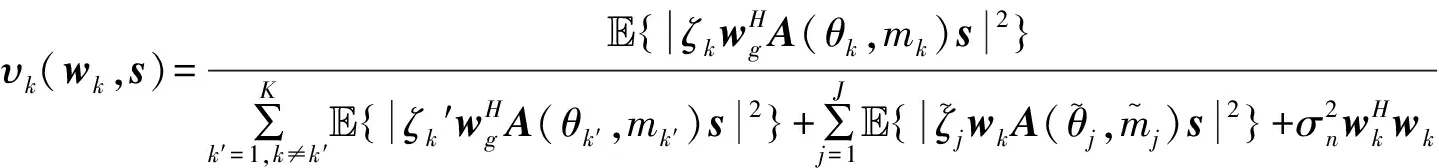
(7)
其中,wk,k=1,2,…,K为对应第k个目标的局部滤波器。

(8)
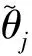
(9)

(10)
其中,Φ(wk)与Ψ(s)为
(11)
(12)
其中,Pj(wj)可以通过参考Pj(wg)得到。
为了对抗环境中存在的信号依赖性干扰,确保雷达的探测性能,这里对空域-快时间滤波器的输出信干噪比进行约束,使滤波器输出的信干噪比不低于某一门限,即
υk(wk,s)≥βk,k=1,2,…,K
(13)
式(13)明确给出了针对雷达波形与滤波器的约束及其数学表达。

Zr=sH(H{r}⊗F{r})s
(14)
式中,F{r}∈L×L的第(u,v)个元素可根据下式计算:
H{r}∈Nt×Nt可由解析式计算得到:

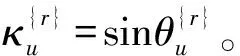
根据以上结果,所要构造的目标函数为
sHΞs
(15)
其中,Ξ∈NtL×NtL为
(16)
其中,ηr>0为第r个己方电磁辐射设备的加权系数。
加权系数的引入可以使雷达操作者根据实际需求灵活地控制在不同空-频范围内的能量压制程度。
综上所述,在信号能量约束下关于设计相容性波形的数学优化问题可归纳为
(17)
其中,ρ为参考信号的比例伸缩系数。
3 优化问题求解方法
为了有效求解优化式(17)中的接收滤波器和发射波形,文献[8]提出了基于DAM[9]的算法框架,但该算法要求初始向量必须在可行域内。为了降低初始值的选取对算法性能的影响,并进一步提高算法收敛性能,本文提出了基于FPP-SCA的相容性波形设计方案。
首先,对变量进行初始化。记初始化波形变量为s{0},且迭代次数p=0。
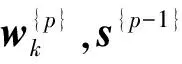
(18)
这是典型的最小方差无失真响应问题,因此式(18)可以等效为

(19)
式(19)有闭式解:
(20)

(21)
其中,
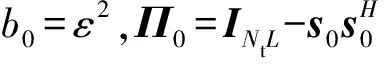
b1=1,Π1=INtL
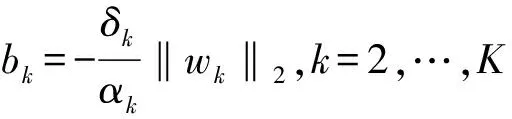
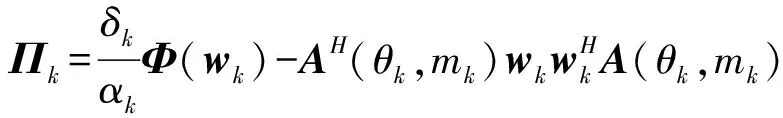
由数学优化理论可知,当存在多个二次约束时,不一定可以直接求解出其最优解,而且二次约束二次优化问题的初始可行点对优化结果会有较大影响。为了解决非凸优化问题即式(21),文献[8]使用对偶上升法的算法框架。为了弱化文献[8]算法中初始点对算法性能的影响,本文采用可行点追踪-连续凸逼近法对该问题进行迭代求解。具体操作如下:
令初始波形向量z0=s{p},假设当前迭代次数为q,求解以下:
subject toυk≥0,k=0,1,2,…,K
(22)
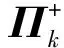
使用SeDumi或CVX工具箱可直接对式(20)进行求解获得yq,并使zq+1=yq,q=q+1。直至收敛目标函数收敛,再使s{p+1}=yq。
最后更新p=p+1,直至式(15)的目标函数收敛,即可获得最优波形。
4 算法性能评估
本节对所提算法收敛性能与文献[8]中基于半正定优化(Semi-Definite Programming,SDP)的相容波形优化算法、基于DAM的相容波形优化算法进行比较,并且明确给出雷达谱图和信号依赖干扰抑制效果图。


表1 目标信息
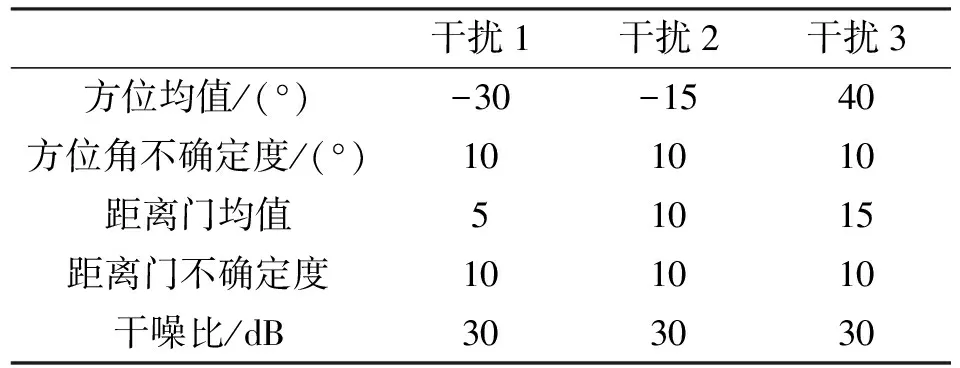
表2 信号依赖性干扰信息

表3 己方电磁辐射体信息
图1对比了不同信干噪比约束下SDP、DAM和FPP-SCA 3种方法的收敛性能。可以看出,在相同信干噪比约束下,本文基于FPP-SCA的方法可以达到更低的收敛值,这是由于FPP-SCA削弱了选取初始值对优化结果的影响;当信干噪比约束门限分别为8 dB和12 dB时,本文算法的收敛值较SDP和DAM分别低8.6 dB和3 dB;当信干噪比约束门限为8 dB时,三种方法的收敛值远低于信干噪比约束为12 dB时的收敛值,这是由于较低的信干噪比门限可以使优化变量获得更多的自由度。
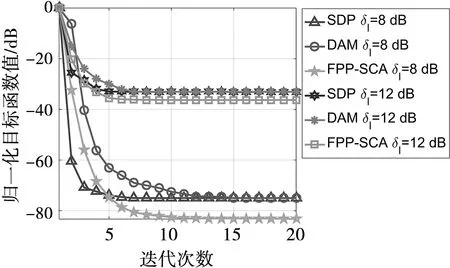
图1 当ε=0.4时在不同信干噪比约束下SDP、DAM和FPP-SCA收敛性能比较
图2给出了ε=0.4、δl=12 dB时MIMO雷达的能量谱。可以清楚看出本文算法使雷达谱在己方电磁辐射体的信号谱分布区域内形成了能量凹陷,减小了电磁辐射体对雷达回波的影响,而且提高了雷达能量的利用率。
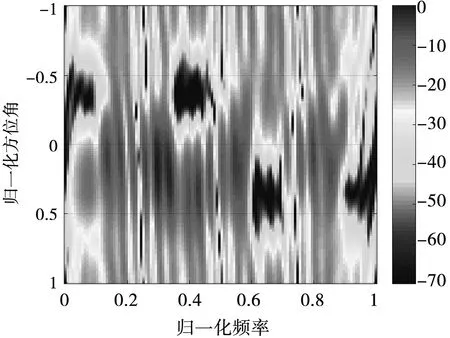
图2 雷达能量谱
为了验证本文算法抑制信号依赖性干扰的有效性,图3给出了对目标所在位置进行滤波时的效果图,其中白色矩形位置标明了信号依赖性干扰的分布区域,黑色圆圈标明了3个目标的位置。图3(a)~(c)分别给出了对3个目标的滤波情况。以图3(a)为例,对目标1进行滤波时,在白色矩形区域内的能量被有效抑制,其他目标位置处形成能量凹陷,这是由于此时滤波器将目标2和目标3视作干扰,对其能量进行了抑制。

图3 信号依赖性干扰抑制效果图
图4统计了取不同初始值对本文方法所获得收敛值的影响,本文算法得到的最终收敛值几乎相同,这是由于FPP-SCA可以减弱初始向量的选取对优化性能的影响。
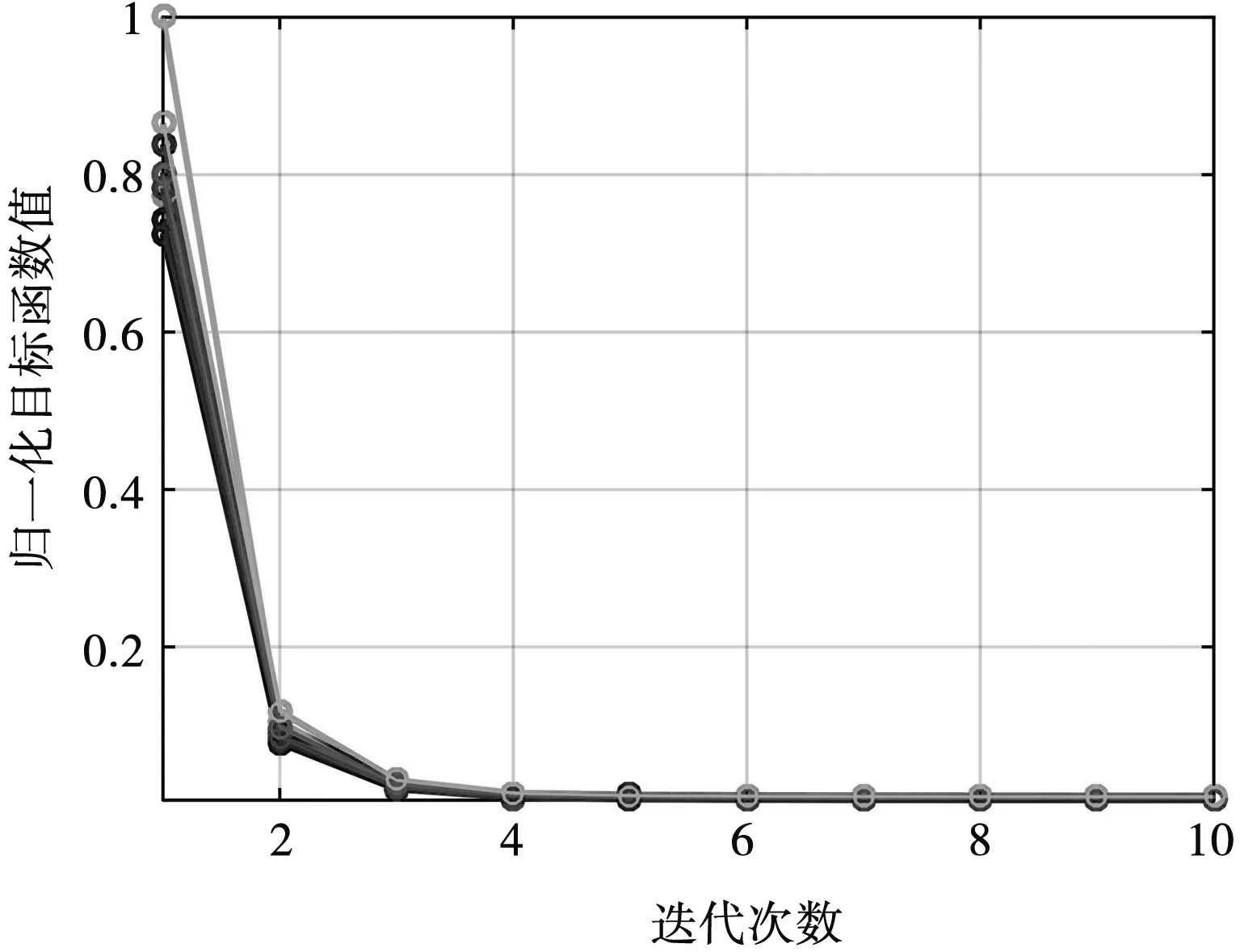
图4 当ε=0.4、δl=12 dB时取不同初始值的目标函数收敛曲线
5 结束语
本文提出了基于FPP-SCA的相容性波形优化方法。相较于已有的基于SDP和DAM的方法,本文方法可以获得更低的收敛值,也就是说可以更好地抑制雷达与己方电磁设备之间的相互影响,可以有力地支持MIMO雷达在未来战场中更好地发挥其出色的探测和抗干扰能力。

