基于等效围压理论的加筋土挡墙土压力计算

张仲伟，张科强，郭鸿*

(1.西安工业大学 建筑工程学院，陕西 西安 710021； 2.陕西理工大学 土木工程与建筑学院)

1 引言

自20世纪60年代开始，加筋土挡墙这类复合型支挡结构便在工程行业内不断推广使用。发展至今，其内部结构形式多样且适用性较强，与传统重力式结构挡墙相比，具有经济性好、适用面广、抗震性能好、承载能力强、可就地取材等优势。因此，近年来被广泛应用于建筑、路桥、边坡治理等工程领域之中。

加筋挡土墙结构的基本原理是在墙背的填料中加入抗拉性能较强的筋带，以弥补墙背填料抗拉性能的不足，通过筋带与土体之间的相互作用限制填料的变形，从而提高复合结构的整体强度和稳定性。由于加筋土挡墙结构中筋带对土体的作用十分复杂，挡墙墙背土压力的大小及分布直接影响挡墙的变形与稳定性，如何考虑筋-土之间的相互作用是挡墙土压力分析与计算的关键因素。

DAXIN E等提出了将筋材对土体的作用等效为附加围压，从而将加筋土看作素土并进行土压力的计算，以简化复合材料的计算方法；杨广庆等基于剪力滞模型计算加筋挡土墙筋带应力和通过试验研究土工格栅加筋挡墙的加筋机理，得到了拉筋的轴向应力及土压力的分布规律；龙建辉等基于极限分析上限法理论，根据加筋挡土墙内部发生破坏时考虑筋-土之间的摩擦损耗，建立分析方程并推导出加筋挡土墙临界高度计算公式；栾茂田等基于有限元模拟的土工格栅挡土墙性能分析，结合RMC足尺试验数据，验证了有限元模拟的可行性；廖红建等基于统一强度理论和等效围压理论，研究了考虑中主应力作用和筋土围压作用下的挡土墙侧向上覆土压力计算方法；Barani O R等提出用一个零厚度的黏结断裂单元模拟土工格栅加筋挡土墙后的滑移面特征，并推导了黏结断裂单元的刚度矩阵，从而有效地模拟了剪切带区域不连续的位移与牵引力；Izzaldin M A等以沙特阿拉伯一个高土工格栅式挡土墙为研究背景，分别利用极限平衡法和Plaxis数值模拟法进行墙侧土压力的计算与分析；俞茂宏建立岩土类材料的统一强度理论，为加筋土复合材料考虑中主应力影响提供了计算基础；介玉新,李广信等提出加筋土计算的等效附加应力法，从而将加筋土看作素土并进行土压力的计算，以简化复合材料的计算。以上专家、学者分别应用理论计算、试验测量和数值模拟手段对加筋土挡墙作用机理进行了剖析，为该文在新平衡状态下考虑加筋等效围压引起大主应力变化而更精确计算土压力提供了重要的参考价值。

加筋土挡墙筋-土作用处于非常复杂的应力状态下，如何合理、正确地考虑筋-土作用关系及机理，是研究墙背土压力大小和分布的基础和关键。以往研究没有考虑加筋效应产生的等效围压在平衡状态下对大主应力的影响，鉴于此，该文基于等效围压理论、统一强度理论及极限平衡理论研究加筋挡土墙土压力计算考虑新平衡状态下大主应力提高的影响，对筋-土复合结构的研究具有重要的理论参考意义。

2 理论计算

2.1 三维等效围压理论

三维等效围压理论即考虑大、中、小主应力的影响，双剪统一强度理论即根据双剪单元体和双剪屈服准则提出双剪统一屈服准则：

(1)

(2)

式中：b为中间主剪应力影响的权系数；σt为材料拉伸屈服极限；τs、σs分别为材料的剪切屈服极限、拉伸屈服极限，其关系为：

b=(2τs-σs)/(σs-τs)

(3)

考虑双剪单元体上全部应力分量对材料破坏的影响，并根据作用于双剪单元体上的两个较大剪应力及其面上的正应力影响函数到达某一极限时，材料开始破坏这一假定，得到适用于岩土材料的双剪统一强度表达式：

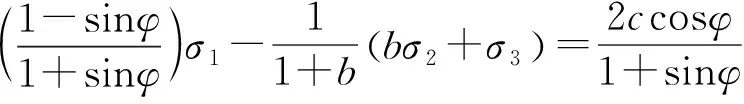
(4)

(5)

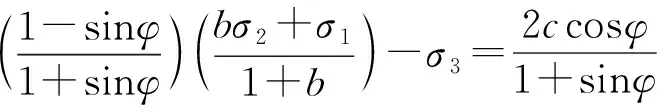
(6)

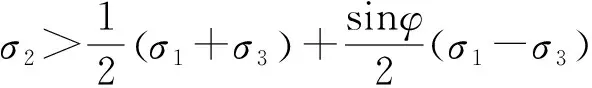
(7)

等效附加围压法是将筋材对土体的作用用一个附加围压代替，如此可将加筋土体当成素土进行分析，以简化计算过程。等效附加围压关系如图1所示。

等效素土双剪统一强度表达式为：

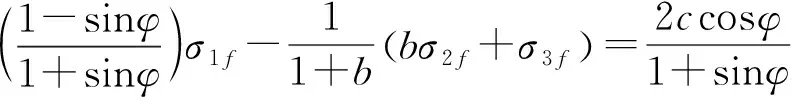
(8)

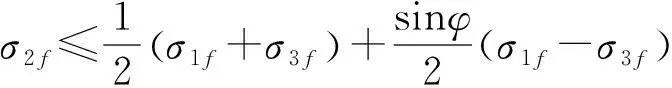
(9)

(10)

(11)

式中：σ1f、σ2f、σ3f分别为新平衡状态下的大、中、小主应力；φ为内摩擦角；c为黏聚力；b为中间主剪应力影响的权系数。

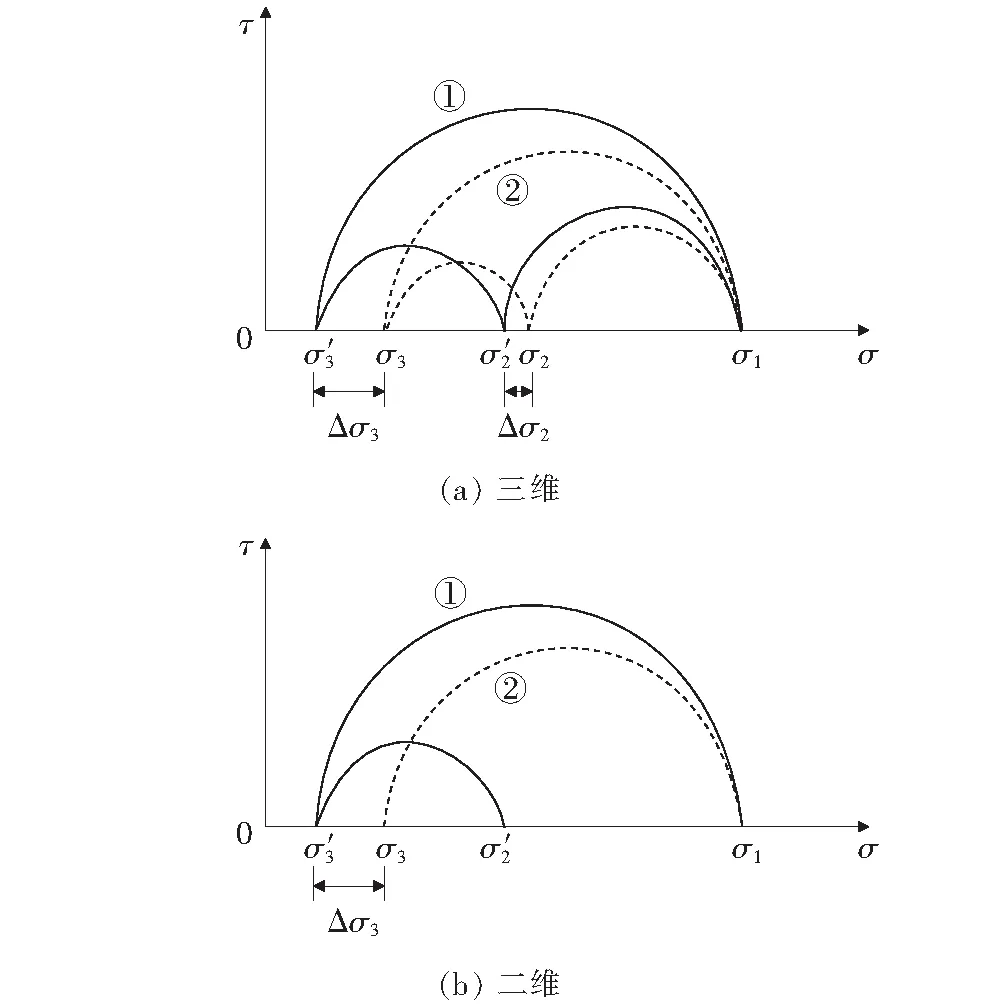
图1 等效附加围压关系

将二维等效附加围压理论推广到三应力状态进行分析：

(12)

式中：R3为筋材小主应力方向上单宽受到的拉力；ΔH为布筋竖向间距。

将式(12)代入双剪统一强度表达式(8)～(11)，可得：

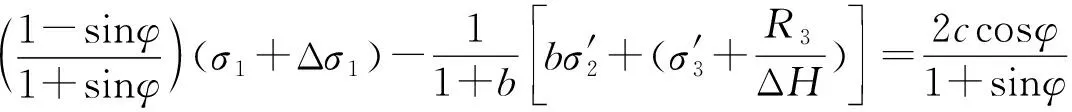
(13)

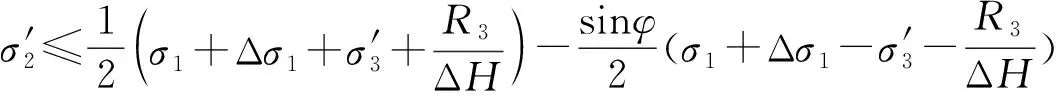
(14)

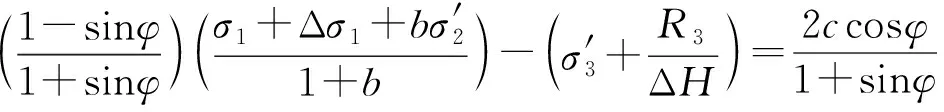
(15)

(16)

在中主应力的计算中引入泊松比ν，当加筋土体处于极限平衡状态时：

σ1=γh，σ′2=ν(σ1f+σ′3)，σ′3=pa

(17)

将式(17)代入式(13)～(16)整理可得土压力计算表达式：

pa=

(18)

(19)

p′a=

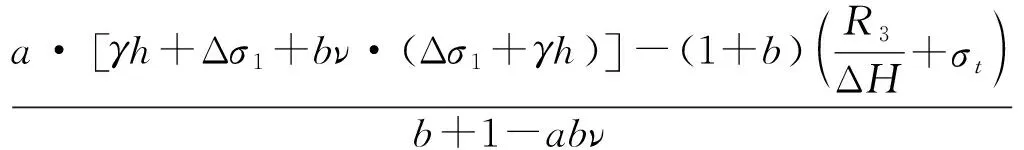
(20)

(21)

式中：pa为主动土压力；γ为土体重度；h为覆土高度。

2.2 二维等效围压理论

极限平衡理论即将加筋挡土墙的土压力分析当成平面问题进行研究，不考虑中主应力的影响，同样基于等效围压理论，根据极限平衡条件建立土体的强度表达式。

未加筋土强度表达式为：

σ1=σ3tan2(45°+φ/2)+2c·tan (45°+φ/2)

(22)

加筋土强度表达式为：

σ1=σ3·tan2(45°+φ/2)+2(c+Δc)·tan (45°+φ/2)

(23)

或者：

σ1=(σ3+Δσ3)·tan2(45°+φ/2)+2c·tan (45°+φ/2)

(24)

由于等效围压Δσ3是由加筋作用引起的，无法直接量取，有资料认为等效围压可依照式(25)计算：

Δσ3/σ3=Δσ1/σ1

(25)

(σ1+Δσ1)=(σ3+Δσ3)·tan2(45°+φ/2)+2c·tan (45°+φ/2)

(26)

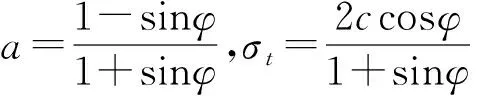
(27)

将式(27)代入式(26)，整理可得：

(28)

3 数值验证

3.1 研究背景

模拟使用Plaxis 2D有限元软件，采用文献[18]的现场加筋土挡墙试验进行土压力的研究。该试验是一墙高为 6.4 m的加筋土挡墙，筋材竖向间距为0.3 m，加筋长度为7 m，不考虑该挡墙施工影响阶段，现场监测数据取稳定阶段进行分析，该阶段挡墙受力由墙后填土和筋带相互作用共同承担。为了简化计算和偏安全考虑，根据不同测点筋材拉力的实测值，取筋材拉力范围的下限值2 kN/m。模拟主体采用平面应变15节点类型，土体采用土与界面中的Mohr-Coulomb类型，土工格栅采用内置土工格栅单元，挡墙面板采用内置板单元，根据文献[18]确定加筋挡墙材料基本参数，如表1～3所示。

表1 填土参数

表2 土工格栅参数

表3 筋-土参数

3.2 模拟过程

建立与文献[18]一致的土工格栅加筋土挡墙模型，分别赋予结构单元相关物理及力学属性，限定初始边界条件，模型网格划分采用土工格栅线性加密，定义初始条件，进行弹塑性模拟分析。

3.3 结果与误差分析

3.3.1 研究结果

加筋挡土墙墙背土压力的大小及分布特征是挡墙设计、维护中最为直接的依据，有效、合理、准确的研究方法可为工程实践提供依据，为设计、分析提供理论参考，以达到最优实施方案。根据三维等效围压理论，取文献[7]最合理值b=0.5计算，对比分析考虑中主应力影响的土压力大小及分布差异，说明数值模拟、试验测量和理论计算3种方法的优缺点。二维等效围压理论是将筋带作用等效为小主应力的影响，而三维等效围压理论是将筋带作用等效为中主应力和小主应力之和的影响，考虑等效因素更为全面，不同方法所得土压力大小及分布规律，如图2所示。

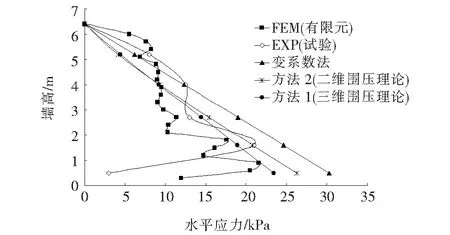
图2 土压力分布

由图2可知：加筋土挡墙的上覆土压力大小随墙高增大，分布为非线性，几种研究方法有所差异，与筋-土复杂应力状态有关;二维等效围压理论计算值相较于三维等效围压理论计算值偏大，其中沿墙高上部约2/3处较为接近，下部偏差随墙高加大而变大，是中主应力的影响结果，三维理论相较于二维理论考虑中主应力的影响，因此计算筋带作用发挥值更高，使得墙背土压力计算值相对二维理论较小，但均较变系数法理论计算值偏小；有限元模拟与试验测量土压力主体分布规律一致，土压力峰值大小接近，但有限元峰值位置偏低，主体土压力偏小。

3.3.2 误差分析

该文二维等效理论及三维等效理论计算土压力的分布均呈近线性分布，加筋考虑为等效附加围压作用，受筋材拉力发挥值影响。而数值模拟相较于试验测量偏于理想状态，没有考虑筋-土摩阻作用力的影响。因此，数值模拟与试验测量方法存在误差，分析产生误差的原因如下：

模拟计算考虑筋带拉力发挥值的影响，并且每层筋带拉力作用值考虑相同，事实上，筋带拉力作用值随上覆土压力、复合挡墙变形等因素的影响，沿墙高不同筋带拉力发挥值不同，进而土压力大小及分布有所不同；筋-土摩阻作用力影响，筋-土摩阻力作用大小随筋带与土体之间的位置变化有所不同，且受变形大小的影响，进而土压力的大小及分布有所不同。

因此，将筋带拉力发挥值和筋-土摩阻作用简化考虑，是影响挡墙土压力计算误差的主要原因。

4 结论

基于等效附加围压理论，分别建立二维和三维土压力计算方法，并结合有限元模拟和文献[18]现场试验数据，得到对应土压力分布规律，得出如下结论。

(1) 土工格栅加筋土挡墙墙背上覆土压力的大小沿墙高增大而变大，土压力呈非线性分布，多种研究方法各有差异，与筋-土复杂应力状态有关。

(2) 考虑中主应力影响的三维等效围压理论相比二维等效围压理论土压力计算值偏小，在墙高约2/3处偏差增大，主要是由上覆土压力的增大引起的，两者均小于变系数法。

(3) 有限元模拟与试验测量土压力分布规律基本一致，呈非线性分布，但有限元应力峰值出现位置略低于试验测量值，处于墙高1/6～1/3范围内，应力峰值大小基本一致。

(4) 该文理论计算和数值模拟受筋带拉力发挥值和筋-土摩阻力作用规律影响，与试验值有所偏差，但能通过理论计算较好地说明中主应力及加筋作用对加筋土挡墙土压力的影响规律。